基于吸引场的蚁群算法在TSP中的应用

王 雷，李 明，刘志虎

（安徽工程大学机械与汽车工程学院，安徽芜湖241000）

基于吸引场的蚁群算法在TSP中的应用

王 雷，李 明，刘志虎

（安徽工程大学机械与汽车工程学院，安徽芜湖241000）

针对传统蚁群算法容易陷入局部最优解等缺陷，提出了一种基于吸引场的改进的蚁群算法.首先，详细分析了基于信息素的吸引场原理，在此基础上建立了基于信息素的吸引场模型.其次，设计了吸引场因子，给出了信息素更新策略，使相距较近的蚂蚁之间能更好地进行协作.最后，针对标准的30个城市的旅行商问题，使用所提出的算法与基本蚁群算法、其他改进的蚁群算法进行优化分析，并进行了结果对比.结果表明：所提出的蚁群算法可以获得TSP问题的最优解423.74，Oliver30问题计算结果最优值为423.74，平均值为423.96，具有较好的搜索全局最优解的能力.

路径规划；旅行商问题；蚁群算法；信息素；吸引场

仿生学家的研究结果表明，蚂蚁个体之间可以通过分泌信息素（pheromone）来传递信息，蚂蚁在行动的过程中会在经过的路径上留下信息素，后面的蚂蚁通过感知这种物质的浓度来选择自己的路径.因此，由大量蚂蚁组成的蚁群的集体行为便表现出一种信息正反馈现象：在较短的路径上留下的信息素浓度较大，因而蚂蚁总是可以找到更短的路径取食.

受自然界中真实蚁群行为的启发，意大利学者Macro Dorigo提出了蚁群算法（ant colony optimization，ACO）［1］，并将其应用于各种优化问题的求解，取得了不错的效果［2-5］.蚁群算法主要是通过蚂蚁群体之间的信息传递而达到寻优的目的，其优点：①具有正反馈机制，通过信息素的不断更新达到查询最优路径；②通用型随机优化方法，它不是对实际蚂蚁的一种简单模拟，而是更多地融入了人的智能；③一种全局优化的方法，不仅求解单目标优化问题，而且可求解多目标优化问题.但是ACO也具有速度慢、易陷入局部最优等缺点.为了克服以上存在的问题，许多学者对基本蚁群算法进行了多方面的改进［6-8］.这些改进方法对一些特定问题的求解已取得了一些效果，但整体而言这些工作还不够完善，仍然需要进一步的研究.文中在分析蚁群算法模型缺陷的基础上，提出一种基于吸引场的蚁群算法（attractive field based ant colony optimization，AFACO）.

1 求解旅行商问题的基本蚁群算法

1.1 旅行商问题路径规划描述

旅行商问题（travelling salesman problem，TSP）的路径规划描述可以描述如下［9］：已知n个城市v=｛v1，v2，…，vn｝，以及任意2个城市之间的距离dij=｛vi，vj｝，求一条经过v中所有城市一次且仅一次的闭合路径｛vx1，vx2，…，vxn｝，使得总的行程最小，即

1.2 基本蚁群算法描述

蚁群算法求解TSP路径规划可以简单表述如下：初始化，将m只蚂蚁随机放在n个网络城市节点上，节点间的每一条边都有初始化信息素тij（0），tabuk（s）表示蚂蚁k的禁忌表，该表的第1个元素设置为其初始节点，它随着蚂蚁的行走动态调整；然后每只蚂蚁依据概率函数（见式（2））选择路线，即选择下一步要去的城市节点，该节点满足j∈allowedk，allowedk是第k只蚂蚁下一步可以选择的节点集，即为

式中：тij（t）为路径i，j上信息素的强度；ηij（t）为节点间距离因子，通常取值为1/dij，其中dij表示节点i，j之间的距离.信息启发式因子α体现信息素在选择概率上的作用（α≥0），期望值启发式因子β体现路径长度在选择概率上的作用（β≥0）.蚁群算法的全局寻优性能，首先要求蚁群的搜索过程必须有很强的随机性；而蚁群算法的快速收敛性能，又要求蚁群的搜索过程必须要有较高的确定性.前者受期望值启发式因子β影响，后者受信息启发式因子α的影响.

当所有蚂蚁都完成一次求解，则完成一次循环.将本次循环找到的最短路径的解作为当前最优解，并按（3）式更新信息素的强度.

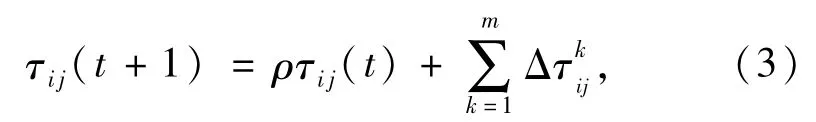
式中ρ为一个取值范围在0到1之间的常数，表示残留信息素的相对重要程度，而（1-ρ）则表示信息素的挥发，是第k只蚂蚁在时刻t到t+1之间，在路径（i，j）上增加的信息素浓度.

式中：Q为一个常量，用来表示每只蚂蚁所释放的信息素总量；Lk为第k只蚂蚁在本次循环中所走路径的总长度.在ant-quantity模型中：

式中dij为第k只蚂蚁在节点i和j之间所走的长度.在ant-density模型中：

它们的区别在于前者利用的是全局信息，而后2种模型中利用的是局部信息.在用传统的蚁群算法中，经过大量试验总结研究，采用式（4）性能较好，所以ant-cycle模型是最优的.

在以上算法中，参数m，ρ，Q，α和β的最佳组合可以由试验而确定，停止条件可以用固定进化代数或者当进化趋势不明显时便停止计算.

1.3 基本蚁群算法分析

蚁群算法本质上仍是一种随机搜索算法，它是通过候选解组成的群体的进化来寻求最优解.算法由许多蚂蚁共同完成，每只蚂蚁在候选解的空间中独立地搜索解，并在所寻得的解上留下一定的信息素.解的性能越好，蚂蚁留在其上的信息素就越多，信息素越多的解被选择的可能性也越大.在算法的最初阶段所有解上的信息素是相同的，随着算法的推进，较优解上的信息素将逐渐增多，算法渐渐趋于收敛［10］.但是，该算法存在一些缺陷，主要归纳为以下2点［11］：①与其他启发式算法相比，它通常需要较长的搜索时间，各种蚁群算法的复杂度可以很好地反映着一点；②蚁群算法容易出现停滞现象.因为在路径规划的初始时刻，各节点或者路径上的信息素的浓度相同，然后通过蚂蚁的路径搜索，不断改变各节点或者路径上的信息素的浓度.但由于蚂蚁之间的协作不足和不够及时，当搜索进行到一定程度后，所有个体发现的解完全一致，不能对解空间进一步进行搜索，不利于得到全局最优的解.另外，路径长短的不同将导致路径上留下的信息素的量的不同，此将对后续的蚂蚁产生一定的影响，基于此文中提出了基于吸引场的蚁群算法，并将之应用于路径规划求解.

2 基于吸引场的蚁群算法

2.1 基于信息素的吸引场原理及吸引场模型

基于信息素的吸引场原理源于蚂蚁的觅食思想，图1为原理示意图.

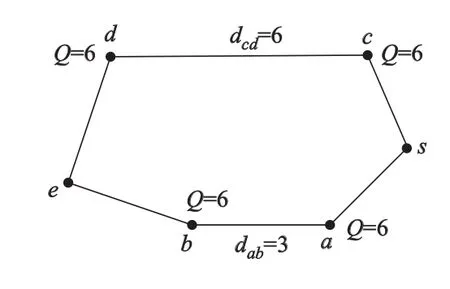
图1 基于信息素的吸引场的原理

在图1中，假设蚂蚁k欲从s到e，其中节点a和b之间的距离dab为一距离很短的路径（dab=3），而节点c和d之间的距离dcd比较大（dcd=6）.假设a，b，c，d和e节点上的信息素大小都为Q=6，同时在此以节点上的信息素量来取代路径上的信息素的量，如用节点a和c上的信息素分别代替路径sa和sc上遗留信息素的量.由于sc比sa短，蚂蚁k将以更大的概率选择c为下一步要到达的位置.但是由于以节点b和d为中心的信息素的浓度将向周围进行扩散，以便对周围路径具有一定的吸引场（吸引力），吸引力的大小假设与距离成反比.由于距离远近的不同，节点a上的信息素的量（Q′=Q+Q/dab= 6+6/3=8）将大于节点c上的信息素的量（Q′= Q+Q/dcd=6+6/6=7），当大到一定程度时，蚂蚁k将以更大的概率选择a节点为下一步要到达的位置，从而使蚂蚁k选择最短路径s-a-b-e的干扰减小.

通过对图1的分析可知，基于信息素的吸引场的强度随着距离的增大而减小，近似服从一个正态分布，如图2所示.

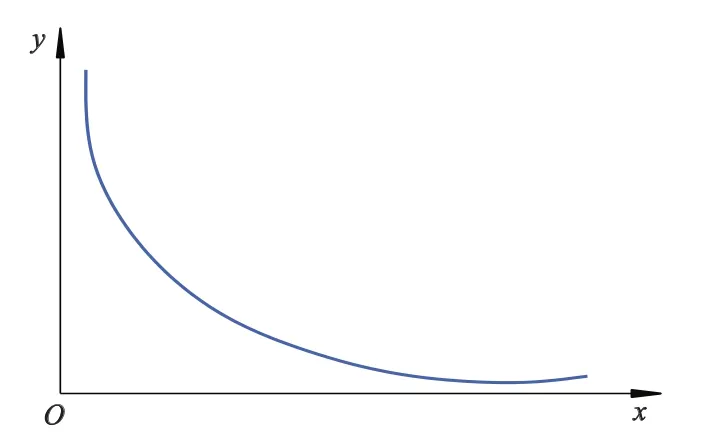
图2 吸引场强度与距离之间的关系模型

图2中横坐标x表示与产生信息素的信源之间的距离，纵坐标y表示吸引场的强度.为了计算的方便，对图2所示的吸引场模型进行了简化，简化结果为

式中Q为一常数.

2.2 基于吸引场的蚁群算法

用蚁群算法求解路径规划，可以表示成图3的形式.

图3 基于蚁群算法的路径规划网络节点优化

图3中椭圆表示第t次访问对应的备选节点集，实心圆表示备选路径对应节点，需要解决的问题是从各组备选节点集中选出一个访问节点，使得所有选择路径最短.如果将每次访问节点看成是蚂蚁爬过的一个节点，则问题的求解过程就可以转化为如何按照1，2，…，n的顺序选择一条路径，使得蚂蚁爬过这一条路径所走过的总路径最短.在图3中，为了便于蚂蚁搜索节点，将所有节点可以进行统一编号.

为了使所求解的问题适合基于吸引场的蚁群算法求解的需要，还需经过适当的设计，由于应用蚁群算法求解问题的关键是确定信息素的变化，为此采用以下信息素的更新策略：

式中：右边的第1项表示蚂蚁k每爬过一段路程，每选择一个结点时，就在该段路程留下局部信息素；λk为吸引场因子；Q为常数，表示信息素的强度为该路程的长度，设i，j分别为该路程的起点与终点，计算式为

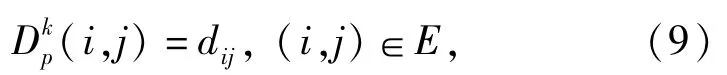
式中E为任务次序约束有向图中的有向边的集合.

式（8）中右边的第2项表示下一个被选集合节点中的节点对该节点吸引力的大小.用allowedk（t）表示蚂蚁k第t次允许爬行的节点，用数组tabuk记录蚂蚁k已经爬过的节点，如allowedk（0）=｛1，2， 3｝，allowedk（1）=｛4，5，6｝，tabuk（0）=0，则计算式写为

吸引场因子λ可以通过以下方式动态调整.首先，蚂蚁所走路径的平均长度为

Lk是蚂蚁k在某一条路径中所走的总长度，在更新信息素时，根据吸引场的原理对所走路径小于¯L的蚂蚁赋予一个相对较大的吸引场因子，路径越短赋予的吸引场因子越大.对于所走路径大于或等于¯L的蚂蚁赋予一个相对小的吸引场因子.其中，吸引场因子λ按式（12）进行调整：

式中：δ为一个很小的正数；ξ为一个很大的正数.由式（12）可见，Lk越接近最优路径的长度（Lmin），吸引场因子λ越接近1.上述算法中首先计算了每次寻优以后所有蚂蚁所走路径的平均值，再根据个体蚂蚁所走路径与该平均值之间的差异来对信息素进行相应地改变，这样就可以增加解空间的多样性，提高蚁群的全局搜索能力，避免出现局部收敛和早熟现象，同时也不会降低蚁群算法的搜索速度.仿真结果表明，改进后的蚁群算法具有更好的搜索最优解的能力.

2.3 基于吸引场的蚁群算法步骤

基于信息素吸引场的蚁群算法的步骤可以描述如下：

1）初始化，初始化m，ρ，Q，α，β，δ和ξ等参数.

2）将m只蚂蚁随机地放置在当n个城市节点上，把第1个城市节点写入禁忌表tabuk中，并设置k=1可访问节点集allowed.

3）t=0，随机选择每只蚂蚁的初始位置，蚂蚁k开始爬行，蚂蚁k根据状态转移概率公式（2）依次选择下一个节点，假设为j，上一个位置假设为i，j∈allowedk（t），t←t+1.

4）将蚂蚁移动到的新节点号加入tabuk中，得到该蚂蚁的路径规划序列.

5）根据公式（8）-（12）进行信息素更新.

6）如果每只蚂蚁都完成了一个完整的路径，则转向7），否则转向3）.

7）如果进化代数大于或等于进化最大代数时，则转向8），否则清空禁忌表tabuk并跳转到2）开始新一轮的进化.

8）输出进化结果，算法结束.

3 仿真试验

为了验证文中算法的实用性及有效性，进行了大量的仿真试验.试验环境如下：windows xp操作系统，英特尔赛扬M440 1.86 GHz的CPU，512 MB内存，80 GB、5 400 r·min-1的硬盘SATA，程序开发软件为Visual C++6.0.

为了验证文中算法的有效性，对经典的TSP路径规划进行了研究.算法中各项参数的取值α=1，β=2，δ=0.01，ξ=1 000，Q=100，ρ=0.9，m=30，N=1 000.图4是对标准的30个城市的Oliver30问题的最终优化结果，进化过程如图5所示.

图4 Oliver30问题的优化结果

图5 寻优进化曲线

从图5可以看出文中算法可以获得TSP的最优解（423.74）.因此，通过文中算法可以自适应地寻找到最短的路径，从而表明该算法的可行性.

表1给出了文中算法在Oliver30上的统计结果.

表1 Oliver30问题计算结果比较

本算法程序独立重复运行20次，将求解的最优解和平均解与其他算法的计算结果进行了对比.由表1可见，在Oliver30问题计算结果的最优值中，文中算法计算得到的最优路径小于基本蚁群算法和蚁群-免疫混合算法［12］的最优路径长度，这说明文中改进的蚁群算法具有较好的搜索最优解的能力.与思维进化算法［13］得到一样的最优值，但在平均值上文中算法计算的结果要优于其他几种算法，从而说明文中算法具有较好的稳定性.

通过大量的仿真试验发现，文中提出的基于吸引场的蚁群算法不但具有基本蚁群算法的分布式并行计算、正反馈机制和鲁棒性强等特点，而且可以较好地克服基本蚁群算法在求解问题时出现的容易陷入局部最优的缺陷，具有加强解得多样性的能力，能够提高算法的全局搜索能力.

4 结 论

1）分析了基于信息素的吸引场原理，给出了吸引场模型，进而提出了一种基于吸引场的自适应蚁群算法.

2）给出了信息素的更新策略以及吸引场因子的动态调整策略；设计了基于吸引场的蚁群算法步骤.

3）TSP路径规划仿真试验结果表明，所提出的蚁群算法可以获得TSP的最优解423.74，Oliver30问题计算结果最优值为423.74，平均值为423.96，具有较好的搜索全局最优解的能力.

（

）

［1］Liao T J，Stützle T，de Oca M A M，et al.A unified ant colony optimization algorithm for continuous optimization［J］.European Journal of Operational Research，2014，234（3）：597-609.

［2］Wu W H，Cheng SR，Wu CC，etal.Ant colony algorithms for a two-agent scheduling with sum-of processing times-based learning and deteriorating considerations［J］.Journal of Intelligent Manufacturing，2012，23（5）：1985-1993.

［3］Wang Lei，Tang Dunbing，Gu Wenbin，et al.Pheromone-based coordination for manufacturing system control［J］.Journal of Intelligent Manufacturing，2012，23（3）：747-757.

［4］黄晓玮，邹小波，赵杰文，等.近红外光谱结合蚁群算法检测花茶花青素含量［J］.江苏大学学报：自然科学版，2014，35（2）：165-170，188. Huang Xiaowei，Zou Xiaobo，Zhao Jiewen，et al.Measurement of anthocyanin in flowering tea using near infrared spectroscopy combined with ant colony optimization［J］.Journal of Jiangsu University：Natural Science Edition，2014，35（2）：165-170，188.（in Chinese）

［5］覃志东，侯 颖，肖芳雄.基于蚁群优化算法的同构多核任务分配与调度［J］.江苏大学学报：自然科学版，2014，35（6）：679-684. Qin Zhidong，Hou Ying，Xiao Fangxiong.Task allocation and scheduling for homogeneous multi-core processors based on ant colony optimization［J］.Journal of Jiangsu University：Natural Science Edition，2014，35（6）：679-684.（in Chinese）

［6］Xiao Jing，Li Liangping.A hybrid ant colony optimization for continuous domains［J］.Expert Systems with Applications，2011，38（9）：11072-11077.

［7］Hannaneh Rashidi，Reza Zanjirani Farahani.A hybrid ant colony system for partially dynamic vehicle routing problem［J］.American Journal of Operational Research，2012，2（4）：31-44.

［8］Mavrovouniotis Michalis，Yang Shengxiang.A memetic ant colony optimization algorithm for the dynamic travelling salesman problem［J］.Soft Computing，2011，15（7）：1405-1425.

［9］张敬敏，马 丽，李媛媛.求解TSP问题的改进混合蛙跳算法［J］.计算机工程与应用，2012，48（11）：47-50. Zhang Jingmin，Ma Li，Li Yuanyuan.Improved shuffled frog-leaping algorithm for traveling salesman problem［J］.Computer Engineering and Applications，2012，48（11）：47-50.（in Chinese）

［10］黄国锐，曹先彬，王煦法.基于信息素扩散的蚁群算法［J］.电子学报，2004，32（5）：865-868. Huang Guorui，Cao Xianbin，Wang Xufa.An ant colony optimization algorithm based on pheromone diffusion［J］.ACTA Electronica Sinica，2004，32（5）：865-868.（in Chinese）

［11］高世伟，郭 雷，杜亚琴，等.一种基于动态加权规则的自适应蚁群算法［J］.计算机应用，2007，27（7）：1741-1743. Gao Shiwei，Guo Lei，Du Yaqin，et al.Adaptive ant colony algorithm based on dynamic weighted rule［J］. Computer Applications，2007，27（7）：1741-1743.（in Chinese）

［12］江新姿，汤可宗，高 尚.蚁群算法与免疫算法的混合算法［J］.科学技术与工程，2008，8（5）：1327-1330. Jiang Xinzi，Tang Kezong，Gao Shang.Hybrid algorithm combining ant colony optimization algorithm with immune algorithm［J］.Science Technology and Engineering，2008，8（5）：1327-1330.（in Chinese）

［13］查 凯，曾建潮.求解TSP问题的思维进化算法［J］.计算机工程与应用，2002，38（4）：102-104. Zha Kai，Zeng Jianchao.Solving TSP with mind evolutionary computation［J］.Computer Engineering and Applications，2002，38（4）：102-104.（in Chinese）

（责任编辑 梁家峰）

Application of an ant colony optimization based on attractive field inTSP

Wang Lei，Li Ming，Liu Zhihu
（School of Mechanical and Automotive Engineering，Anhui Polytechnic University，Wuhu，Anhui241000，China）

To overcome the default of local optimal solution in the traditional ant colony algorithm，a modified ant colony optimization（AFACO）was proposed based on attractive field.The principle of attraction field based on pheromone was analyzed in detail to establish the attractive field model.The attractive field factor based on pheromone was designed，and the pheromone updating strategy was provided to improve the collaboration among ants nearby.For the standard 30 city traveling salesman problem，the optimization results from the proposed algorithm were compared with those from basic ant colony algorithm and some other improved ant colony.The results show that the optimal solution of TSP problem is 423.74，while the optimal and the mean solution of Oliver30 are 423.74 and 423.96，respectively，which shows the improved ant colony algorithm has good ability for searching the global optimal solution.

path planning；travelling salesman problem；ant colony optimization；pheromone；attractive field

TP183

A

1671-7775（2015）05-0573-05

王 雷，李 明，刘志虎.基于吸引场的蚁群算法在TSP中的应用［J］.江苏大学学报：自然科学版，2015，36（5）：573-577，582.

10.3969/j.issn.1671-7775.2015.05.014

2014-12-01

国家自然科学基金资助项目（51305001，71171002）；安徽省自然科学基金资助项目（1308085ME65）；安徽省高等教育提升计划省级自然科学研究项目（TSKJ2014B12）

王 雷（1982—），男，安徽亳州人，副教授，博士（wangdalei2000@126.com），主要从事数字化设计与智能制造研究.

李 明（1986—），男，安徽宿州人，硕士研究生（1039518062@qq.com），主要从事机器人路径规划研究.