基于Kriging法的挖掘机驾驶室减振器性能参数优化

刘 磊，周以齐，米永振，卢 丹，陈跃彪

（1.山东大学机械工程学院，山东济南250061；2.山东大学高效洁净机械制造教育部重点实验室，山东济南250061）

基于Kriging法的挖掘机驾驶室减振器性能参数优化

刘 磊1，2，周以齐1，2，米永振1，卢 丹1，陈跃彪1

（1.山东大学机械工程学院，山东济南250061；2.山东大学高效洁净机械制造教育部重点实验室，山东济南250061）

针对挖掘机驾驶室内噪声抑制问题，建立了挖掘机整机的有限元模型，通过驾驶室减振器性能参数的优化，实现了驾驶员耳旁噪声声压级曲线上的多个峰值及总声压级的降低.其中，采用拉丁超立方法对减振器参数刚度和阻尼设计试验，仿真计算得到样本点后建立Kriging代理模型；以耳旁声压级曲线上多个峰值频率处的声压级为目标函数、以减振器性能参数为优化变量，通过NSGA-Ⅱ遗传算法进行优化并得到相应的Pareto前沿.选定减振器性能参数最佳组合再次代入有限元模型中仿真计算，结果表明：通过优化减振器性能参数降低驾驶员耳旁噪声峰值频率处声压级和总声压级的方法可行，挡风玻璃处、座椅处地板及仪表盘处为代表的观测点的振动噪声性能也有改善.

减振器；参数优化；试验设计；Kriging代理模型；耳旁噪声

驾驶室内噪声影响驾驶员身心健康，降低工作效率，增大安全隐患.驾驶室内噪声的抑制是工程机械NVH（noise，vibration，harshness）问题研究的热点.驾驶室内噪声可按传递路径分为空气噪声和结构噪声.车身结构振动产生的中低频的结构噪声是造成驾驶员强烈不适感的主要来源.而减振器作为连接车架与驾驶室的部件，是振动信号的主要传递路径.对减振器的性能参数进行分析优化，可有效削弱车架传递至驾驶室的振动能量，降低驾驶室内结构噪声水平.

目前，通过优化减振器性能参数以实现机械设备减振降噪的研究已有很多.刘顺安等［1］基于IPSO算法对汽车减振器包括刚度在内的9个主要参数进行优化，从而改善减振器压缩、复原行程的阻尼特性和对外界振动的缓冲、衰减性能，提高了汽车的平顺性和舒适性；张俊红等［2］基于BP神经网络算法对柴油机轴系扭振减振器的扭转刚度、阻尼系数等参数进行参数优化设计，实现了轴系在工作转速范围内共振振幅的显著降低；R.Alkhatib等［3］提出一种基于遗传算法的减振器参数优化方法，实现线性单自由度减振模型参数优化，并应用于汽车悬挂模型的刚度、阻尼参数优化过程，提升了减振器的减振隔振性能.

由上述可知，通过优化减振器参数改善机械设备的振动特性是可行的.而实际研究中，以降低挖掘机驾驶员耳旁噪声为目标的驾驶室减振器性能参数优化尚不多见.笔者在20～250 Hz的频率范围内［4］，选取驾驶室6个减振器的刚度、阻尼为优化变量，2个峰值频率上的声压级为目标函数，建立基于Kriging响应面的多目标优化模型，得到相应的Pareto最优解集，确定减振器的最优性能参数组合.

1 整机有限元模型的建立

1.1 车身有限元模型

将某型挖掘机三维模型导入HyperMesh软件，共包括驾驶室和车架2部分.采用四边形壳单元对驾驶室结构进行离散，而车架结构采用四面体实体单元，单元尺寸均为15 mm，最终分别得到207 867和355 293个单元.此外，采用ACM单元模拟焊接位置，共生成123 586个［5-6］.有限元模型如图1所示，驾驶室底部通过左右对称分布的6个橡胶减振器与车架相连接，编号1-6分别代表驾驶室左前部、右前部、左中部、右中部、左后部和右后部减振器，在软件中由3向弹簧-阻尼器连接单元cbush模拟.cbush单元可定义6个空间自由度上的刚度和阻尼.车架的激励集中于垂直方向，在引起驾驶室壁板振动方面起主要作用，故将垂直方向平动自由度的减振器参数作为研究重点.

图1 挖掘机整机有限元模型及驾驶室减振器位置分布示意图

不同部位所划分的单元分别赋予相应的材料属性，其参数如表1所示.

表1 模型中各材料属性的参数

1.2 声-固耦合系统

对驾驶室有限元模型进行处理，添加座椅、建立适当连接；去除对声学分析影响小的部件；适当填补模型中的小孔和缝隙，使其形成封闭的结构有限元模型.

在进行声学仿真时为保证分析精度，声学网格单元长度应满足：

式中：L为网格单元长度；c为声速；fmax为最高计算频率.

一般挖掘机动力系统组件的优势结构激励的上限频率为250 Hz，驾驶室板件振动辐射声能量也主要集中在中低频段［7］，故分析最高频率为250 Hz.综上，取声腔单元尺寸为50 mm，进而抽取驾驶室内部声腔.得到了含有37 229个六面体实体单元的声腔有限元模型如图2所示.

驾驶室壁板结构系统与声腔系统通过边界节点上的振动进行耦合连接.在有限元模型中，定义了声腔边界节点与临近的结构节点共用，实现声腔和结构的相互耦合.在声固耦合系统中，联立结构有限元方程和声腔有限元模型，得到声-固耦合系统的有限元方程［4］：

式中：s，p分别为车身结构位移矢量和节点声压矢量；mss，kss分别为车身质量矩阵、刚度矩阵；mff，kff分别为声学的质量矩阵、刚度矩阵；ρ0为空气密度；S为结构-声学耦合矩阵；F为施加于车身上的外力矢量.

由式（2）可知：驾驶室壁板结构的力学特性和声腔的声学特性共同决定了耦合系统的声压分布，由作用在车身结构上的外力F即可求出驾驶室内各节点处的声压.

1.3 驾驶室场点声压预测

为了预测车内的结构噪声水平以及验证有限元模型的准确性，在怠速工况下采集4个发动机支座上的加速度信号和驾驶室内耳旁节点的声压信号，如图3所示.

图3 发动机支座处传感器及驾驶室内的传声器

将测得的加速度信号作为声固耦合模型的激励加载到有限元模型的相应部位，按照实际情况约束车架底部圆台上的部分节点，将原垂直方向上减振器的刚度、阻尼参数赋予到cbush单元属性.

选取20～250 Hz频率范围建立频响分析工况并求解.驾驶员耳旁节点声压级曲线的计算结果和由传声器采集的试验结果如图4所示，f为频率，Lp为声压级.

图4 驾驶员耳旁节点声压级曲线

观察图4可以发现驾驶员耳旁噪声的计算值和试验值比较吻合.由于外界噪声干扰、力学模型简化等因素，两者在声压级幅值上有一定差异，但计算值能够反映试验值的整体特征.因此，建立的整机有限元噪声预测模型具有较高精度，可用于驾驶员耳旁噪声的预测.另外，从图4可以看出：213 Hz和233 Hz处振动能量较集中，存在突出的声压级峰值，分别为84.6，97.2 dB，频段上总声压级为87.8 dB.由声压级叠加原理可知峰值频率处声压级大小对总声压级水平具有主导作用［8］.因此，将以213 Hz和233 Hz处的声压级为目标函数进行减振器性能参数优化.

2 代理模型的建立

驾驶室减振器的刚度、阻尼与驾驶员耳旁噪声声压级之间的关系复杂，难以实现显式表达.基于试验设计、数理统计和近似方法的Kriging代理模型，能利用较少的训练样本点，以较高的精度拟合建立设计变量与响应之间的函数关系，实现对未知点响应的预测［9］，因此将其用于减振器性能参数与噪声声压级间函数关系的建立.

2.1 K riging模型的基本理论

在基于插值方法所建立的计算程序Kriging代理模型中，设计变量与响应之间的数学关系可以表示为

式中：y（x）为待模拟的未知函数；g（x）为全局近似模型的多项式函数；z（x）为对局部偏差的拟合，是随机分布函数.

z（x）满足统计特征：

式中：R为相关矩阵；xi，xj为样本点；R（xi，xj）为任意2个采样点间的相关函数.

R（xi，xj）常取高斯函数形式：

式中：n为设计变量个数；θk为未知的相关参数矢量和是样本点xi，xj第k维元素.

待测点x处，其预测响应值为

式中：Y为N个采样点的响应值列向量；e为长度为N的单位列向量；r（x）为待测点x与采样点之间的相关函数构成的相关向量.

r（x）可以表示为

且由最小二乘估计可得模型参数为

方差的估计值为

由于模型的参数β和方差估计值σ2均为θk的函数，Kriging模型的最终形式由θk的取值决定［10］，而θk的最优取值可由最大似然估计法解出：

由式（10）求得θk，在解出参数β和α2后，进而可求得到Kriging模型.

2.2 仿真结果采样

充足准确的样本数据是获得高质量代理模型的前提.拉丁超立方采样方法基于多维分层抽样理论，能均匀地研究各个试验因素的各个水平，避免重复抽取已出现的样本点.能够以较少的试验点数准确反映设计空间的特性，计算效率高，适合于含多设计因素的代理模型的建立［11］.

将驾驶室6个减振器在垂直方向上的刚度Ki和阻尼Ci（i=1，2，…，6）作为12个设计因素，采用拉丁超立方采样进行试验设计，Ki取值范围为108～132 N·mm-1，Ci取值范围为1.2～4.8 N·s·mm-1.

为使试验点能均匀地充满设计空间，试验次数至少为2n次.为保证Kriging代理模型的精度，取100组仿真计算样本数据用于建立代理模型.基于已建立的整机有限元模型，经仿真分别得到在不同的刚度和阻尼参数组合下驾驶员耳旁噪声213 Hz和233 Hz处的声压级数据Lp1和Lp2.样本点的部分仿真结果如表2所示.

表2 拉丁试验设计的仿真结果

2.3 建立K riging模型

将213 Hz和233 Hz处的噪声声压级Lp1和Lp2作为响应输出值.基于已得的仿真结果，建立了2个Kriging模型.其中，以Lp1为响应值的Kriging模型A的参数θk1=［5.38，3.25，4.35，1.19，0.72，0.43，1.28，0.95，0.10，0.52，0.42，0.10］；以Lp2为响应值的Kriging模型B的参数θk2=［2.25，1.24，0.68，0.37，19.87，19.86，0.10，0.10，19.81，19.95，1.51，7.39］.

代理模型建立后，需对其准确性进行检验.采用相对均方根误差RMSE以及判定系数R2作为精度分析指标［12］.RMSE值越小，R2越接近1，则模型精度越高，响应面与真值之间的差异程度越低，其表达式如下：

式中：nv为测试点个数分别为针对测试点的仿真计算值、仿真计算值的平均值、Kriging代理模型预测值.

采用拉丁超立方采样方法随机抽取20组检测点，并分别进行有限元仿真计算和Kriging代理模型预测计算.RMSE和R2的值如表3所示，2个代理模型均具有较高的拟合精度，可据此结合多目标遗传算法进行减振器性能参数的优化.

表3 代理模型的RMSE和R2值

3 多目标优化模型的建立

3.1 优化数学模型

由上文分析可知：该问题存在2个目标函数，分别为213 Hz和233 Hz处的声压级Lp1和Lp2，优化变量为6个减振器在垂直方向上的刚度Ki和阻尼Ci，i=1，2，…，6.该优化的数学模型可描述为

3.2 优化过程及结果分析

多目标遗传优化算法基于生物进化理论，由初始种群经过选择、交叉和变异遗传操作反复迭代构造非支配解集，从而不断逼近最优Pareto解集［13］.文中采用的NSGA-Ⅱ算法，引入了快速非支配排序算法、拥挤度比较算子及精英策略，在降低计算复杂度缩短计算时间的同时，具有更好的收敛性和鲁棒性［14］.

基于已建立的2个Kriging代理模型和优化数学模型，设置的算法参数：最优前端个体系数为0.35；初始种群大小为180；迭代计算的停止标准是最大进化代数与停止代数均为2 400或适应度函数值的偏差为10-4，并在求解过程中绘制Pareto前沿.参数优化计算完成之后，得到此多目标优化问题的Pareto前沿如图5所示.

图5 减振器参数优化问题的Pareto前沿

图5中，每个点分别对应1组驾驶室减振器的刚度和阻尼参数组合，这些点的集合即构成了Pareto最优解集.分析优化结果后可以发现：不同的减振器性能参数组合下，213 Hz和233 Hz处声压级Lp1和Lp2有显著差异，选取适当的参数组合，可以有效降低213 Hz和233 Hz处的声压级水平；以上2个优化目标之间存在明显的优化矛盾，并不存在唯一的全局最优解使各目标均达到最优，Lp1和Lp2中任一函数值的降低都必须以提高另一个目标函数值为代价.

在综合对比Pareto前沿中2个声压级的大小和变化幅度后，将图5中椭圆区域包含的Pareto解所对应的减振器性能参数组合分别赋予到cbush单元属性中进行频响分析，得到驾驶员耳旁节点声压级数据.在比较筛选后确定最优解为图5中红色点所示解.其对应的减振器性能参数组合：K1-K6分别为108.5，114.3，117.2，128.1，127.0，118.2；C1-C6分别为3.59，1.44，1.85，2.33，1.56，3.35.

减振器参数优化前后，驾驶员耳旁声压级曲线和前挡风玻璃处（与驾驶员右耳等高）声压级曲线及1/3倍频程声压级分别如图6-9所示，座椅处地板的振动加速度曲线及仪表盘处的加速度曲线分别如图10，11所示，a为加速度.

图6 减振器参数优化前后的驾驶员耳旁同一节点的声压级曲线

图7 减振器参数优化前后的驾驶员耳旁同一节点的1/3倍频程声压级

图8 减振器参数优化前后前挡风玻璃附近声腔同一节点的声压级曲线

图9 减振器参数优化前后前挡风玻璃附近声腔同一节点的1/3倍频程声压级

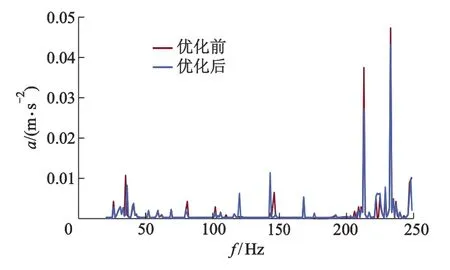
图10 减振器参数优化前后座椅处地板同一节点的振动加速度曲线

图11 减振器参数优化前后仪表盘处同一节点的振动加速度曲线

由图6可观察到213 Hz处和233 Hz处声压级有显著下降，分别降低至87.8 dB和68.1 dB.图7中1/3倍频程声压级柱状图也表明200～280 Hz频段内声压级有所下降.尽管部分频率处的声压级有所上升，但综合20～250 Hz范围内，驾驶员耳旁噪声总声压级降低了2.6 dB，达到了85.2 dB.

观察图8-11可以发现：优化前后挡风玻璃处的声压级在233 Hz处峰值显著下降，1/3倍频程声压级柱状图9表明：多处频段范围内声压级都略有降低，经计算，20～250 Hz范围内总声压级降低了1.1 dB；座椅处地板节点的振动加速度幅值在213 Hz频率处有明显下降，其他频率处无明显变化；仪表盘处节点的振动加速度幅值在105，213，233 Hz处均有小幅度下降.因此，该优化方法在降低了驾驶员耳旁噪声的同时，对挡风玻璃处、座椅处地板及仪表盘处为代表的观测点的振动噪声性能亦略有改善.

4 结 论

1）建立了挖掘机整机的有限元声固耦合模型，通过试验验证，可有效预测驾驶员的耳旁噪声.

2）以挖掘机驾驶员耳旁噪声声压级曲线上的多个峰值为目标函数，以驾驶室减振器垂直方向上的刚度和阻尼参数为优化变量，进行了优化计算.可用于指导降低驾驶室内的噪声水平，提高挖掘机驾乘舒适性.

3）在拉丁超立方试验设计采样的基础上建立的Kriging代理模型，能较好地模拟驾驶员耳旁噪声声压级峰值与减振器性能参数之间复杂的函数关系，与多目标遗传优化算法相结合，可完成驾驶室减振器性能参数的优化，得到合理有效的Pareto最优解集.

（

）

［1］刘顺安，胡庆玉.基于IPSO算法的减振器优化［J］.吉林大学学报：工学版，2010，40（2）：341-345. Liu Shun′an，Hu Qingyu.IPSO algorithm for optimization of shock absorber［J］.Journal of Jilin University：Engineering and Technology Edition，2010，40（2）：341-345.（in Chinese）

［2］张俊红，倪广健，郑 勇，等.基于BP神经网络的柴油机轴系扭振减振器优化设计［J］.内燃机学报，2008，26（1）：83-86. Zhang Junhong，Ni Guangjian，Zheng Yong，et al.Optimum design of torsional damper of diesel engine crankshaft system based on BP neural network［J］.Transactions of CSICE，2008，26（1）：83-86.（in Chinese）

［3］Alkhatib R，Nakhaie Jazar G，GolnaraghiM F.Optimal design of passive linear suspension using genetic algo-rithm［J］.Journal of Sound and Vibration，2004，275：665-691.

［4］马天飞，高 刚，王登峰，等.基于声固耦合模型的车内低频结构噪声响应分析［J］.机械工程学报，2011，47（15）：76-82. Ma Tianfei，Gao Gang，Wang Dengfeng，et al.Response analysis of interior structure noise in lower frequency based onstructure-acoustic coupling model［J］. Journal ofMechanical Engineering，2011，47（15）：76-82.（in Chinese）

［5］王良模，陈东益，邹小俊，等.某轻型卡车正面A柱撞击仿真与改进［J］.江苏大学学报：自然科学版，2014，35（2）：132-136. Wang Liangmo，Chen Dongyi，Zou Xiaojun，et al.Simulation and improvementofa light truck in A-pillar impact［J］.Journal of Jiangsu University：Natural Science Edition，2014，35（2）：132-136.（in Chinese）

［6］王若平，毛国威.基于MSC.NASTRAN的城市客车模态分析［J］.重庆理工大学学报：自然科学，2014，28（4）：1-4. Wang Ruoping，Mao Guowei.Modal analysis of city coach body frame based on MSC.NASTRAN［J］.Journal of Chongqing University of Technology：Natural Science，2014，28（4）：1-4.（in Chinese）

［7］张志勇，张义波，刘 鑫，等.重型卡车驾驶室结构噪声预测与板件声学贡献度分析［J］.振动与冲击，2014，33（13）：67-71. Zhang Zhiyong，Zhang Yibo，Liu Xin，et al.Structureborne noise prediction and panel acoustic contribution analysis of a heavy-duty truck cab［J］.Journal of Vibration and Shock，2014，33（13）：67-71.（in Chinese）

［8］王二兵，周 鋐，徐 刚，等.基于车身板件声学贡献分析的声振优化［J］.江苏大学学报：自然科学版，2012，33（1）：25-29. Wang Erbing，Zhou Hong，Xu Gang，et al.Acousticvibration optimization based on panel acoustic contribution analysis of vehicle body［J］.Journal of Jiangsu University：Natural Science Edition，2012，33（1）：25-29.（in Chinese）

［10］Gaspar B，Teixeira A P，Guedes-Soares C.Assessment of the efficiency of Kriging surrogatemodels for structural reliability analysis［J］.Probabilistic Engineering Mechanics，2014，37：24-34.

［11］Park J，Lee K S，Kim M S，etal.Numerical analysis of a dual-fueled CI（compression ignition）engine using Latin hypercube sampling and multi-objective Pareto optimization［J］.Energy，2014，70：278-287.

［12］Liu Yang，Li Yan，Wang Dejun，et al.Model updating of complex structures using the combination of componentmode synthesis and kriging predictor［J］.The ScientificWorld Journal，2014，208：1-13.

［14］Murugan P，Kannan S，Baskar S.NSGA-II algorithm for multi-objective generation expansion planning problem［J］.Electric Power Systems Research，2009，79（4）：622-628.

（责任编辑 贾国方）

Performance parameter optim ization of excavator cab shock absorbers based on Kriging method

Liu Lei1，2，Zhou Yiqi1，2，Mi Yongzhen1，Lu Dan1，Chen Yuebiao1
（1.School of Mechanical Engineering，Shandong University，Jinan，Shandong 250061，China；2.Key Laboratory of High Efficiency and Clean Mechanical Manufacture，Ministry of Education，Shandong University，Jinan，Shandong 250061，China）

To solve the problem of restraining noise in excavator cab，the FEM model ofwhole excavator was established，and the performance parameters of cab shock absorbers were optimized to reduce the sound pressure level（SPL）peaks and the overall SPL at driver right ear（DRE）.Based on the sample points from Latin Hypercube experiment of stiffness/damping parameters of shock absorbers，the Kriging surrogatemodelwas constructed.The Pareto frontwas obtained by NSGA-Ⅱgenetic optimization algorithm with several SPL peaks as objective functions and performance parameters of shock absorbers as variables.The FEM simulationswere re-analyzed by the optimum combination of performance parameters. The results indicate that it is practicable to decrease the SPL peaks and the overall SPL at DRE by adjusting performance parameters of cab shock absorbers.The vibration noise performance at the representative places of the windshield，the floor under seats and the dashboard are also improved.

shock absorber；parameter optimization；experiment design；Kriging surrogatemodel；SPL at DRE

U415.51

A

1671-7775（2015）05-0497-07

刘 磊，周以齐，米永振，等.基于Kriging法的挖掘机驾驶室减振器性能参数优化［J］.江苏大学学报：自然科学版，2015，36（5）：497-503.

10.3969/j.issn.1671-7775.2015.05.001

2015-01-21

国家科技支撑计划项目（2012BAH09B03）；济南市科技重大专项（201208003）

刘 磊（1990—），男，山东临沂人，硕士研究生（liuleisddx@126.com），主要从事挖掘机驾驶室内降噪研究.

周以齐（1957—），男，山东济南人，教授，博士生导师（yqzhou@sdu.edu.cn），主要从事工程机械整机减振降噪、消声器设计研究.