基于误差概率补偿修正的短期负荷预测研究
周 剑,邵常宁,陈 刚,刘 梅,赵 燃
(1.南方电网电力调度控制中心,广州 510623;2.北京清软创新科技有限公司,北京 100085)
随着我国电网规模和复杂程度的日益扩大,电源与负荷种类繁杂,电网平衡难度加大,对电网精细化管理的要求越来越高。短期负荷预测是电力需求侧管理的重要内容,也是电网调度部门指导编制日前发电计划的依据,是电力系统安全稳定经济运行的重要保障。传统的短期负荷预测方法已经无法适应新形式下电网精细化管理的要求,其局限性主要体现在2个方面。首先,传统的预测思路往往从历史负荷正向出发,对负荷自身规律进行研究,没有对预测误差引起足够的重视。预测误差往往蕴含着某些特定因素的关键信息,忽略预测误差意味着放弃了对这部分信息分析和利用;其次,负荷的本质决定了负荷不具有完全可预测性,而现有的大量预测方法给出的均是确定性的预测结果,只能给出负荷的一种可能的发展趋势,无法体现负荷的概率波动。如果可以通过概率分析得到负荷发展的诸多可能性以及其对应的概率区间,对负荷进行概率性补偿预测,就可为预测工作提供更加精细的决策依据。
为了解决上述2个问题,本文通过研究某大区电网历史负荷预测误差的概率分布特性,进而对确定性的预测结果进行概率补偿,得到一定置信水平下的负荷概率预测结果。概率补偿预测可以帮助电网企业充分了解现行预测流程下误差的统计规律,更好的把握在进行生产计划、安全校核等工作中面临的不确定性,满足市场化日益增长不确定性风险决策需求。
1 误差概率统计及补偿预测原理
误差概率统计及概率补偿预测总体流程如图1所示。

图1 误差概率统计及补偿预测原理
首先对采集到的历史值进行预处理以提高数据质量,得到准确的历史预测误差样本。考虑误差的分布与时段及负荷水平有关,对历史样本做恰当的层次划分。在此基础上对划分出的每一个小区间统计其误差概率分布,然后对其他的历史样本进行校验以验证误差统计的规律性。校验通过之后对确定性负荷预测结果进行概率补偿修正,得到一定置信水平下的负荷预测概率波动区间,即获得负荷的不确定性预测结果。
1.1 历史不良数据辨识与修正
丰富而准确的历史数据是负荷分析和预测工作的前提,预测前有必要对历史不良数据进行辨识与修正。现行的几种种常用的不良数据辨识修正方法包括神经网络法、基于聚类分析及模糊理论的方法、间隙统计法(GSA)、残差修正法等[1],主要针对大量历史数据的自动辨识修正。本文研究的历史样本仅为一个月,数据较少,采取如下的简单辨识方法。
(1)确定历史样本
设历史样本第i天t时刻的负荷为Pi,t,(i=1,2,…,n,t=1,2,…,T),n为历史天数,T为采样点数。第s天为第i天的同类型日,s=i±7,则其t时刻的历史负荷为Ps,t。
(2)逐点计算负荷偏差率

设定偏差率的阈值,超过阈值则视为不良数据需进行修正,不超过阈值则视为有效数据。
(3)不良数据校正
采取参考日负荷基础上的平均增长作为不良数据的校正值

1.2 误差概率统计

后文所指的误差均指相对误差。一般来讲,求其随机事件发生的概率密度分布需要事先了解分布函数,通过典型分布函数的数学模型求导获得。本文的研究对象不具备典型性,采用直接数据统计的方法对历史误差进行归类统计,得到统计意义上的离散概率分布,能够客观反映历史误差的规律性。
为了更加准确的把握历史误差的概率分布情况,本文采用分时段和分负荷水平2个层次进行误差概率统计。采用分层次分析具有2个依据:负荷所处时段的不同具有不同的误差分布特性,如:峰时、谷时和平时段的误差规律各不相同;不同负荷水平下误差分布特性也具有区别,一般规律为:高负荷的误差较大而低负荷时误差较小。因此本文建立了考虑时段和负荷水平的联合二维概率分布,设每个划分的每个小区域为Dkt,其中k代表时段,t代表负荷水平划分。时段的划分依据一般按照高峰、低谷和平段分为3—5个时段,负荷水平的划分则要遵循落入每段负荷水平内的样本个数尽可能相等的原则。设共划分有M个时段,在某个时段共有样本个数S个,负荷水平层次划分为N个区间,当负荷水平小于Pt时的样本个数为g(Pt),则负荷水平区间的划分依据为
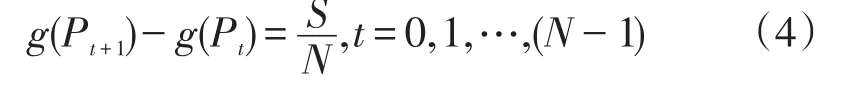
其中P0为该时段内的最小负荷。通过式(4)解得负荷水平Pt得到各个负荷水平划分区间的端点。
经过上述出力后将整个时段—负荷区域分成M×N个小区间。设第k时段和第t负荷水平段的样本数为Rkt,相对误差落在s区间内的样本频数为ωs,则可得此区间上的离散频率分布

当Rkt充分大时fs可近似的视为该区间上的离散概率密度。按上述方法可分别得到M×N个小区间的离散概率密度[2]。
1.3 概率补偿预测修正
概率补偿预测修正即根据待预测日每一点负荷的确定性预测结果,结合上文中所分析的离散概率密度进行补偿,在一定置信水平下得到负荷概率波动区间。在概率补偿预测之前需要先进行层次误差概率密度的检验。
设研究历史样本集合为I1,可选取与时间相近的足够数量的样本集合I2,按照同样的方式得到在统一的区间划分的基础下的离散概率密度。可用皮尔逊系数检验2类离散概率密度的相关性强弱[3]

式中:xi、yi分别为样本集合I1、I2中某时段、某负荷层次下的误差概率,分别为对应的概率均值。相关系数越接近1,则证明2个历史样本的预测误差概率波动规律越相似,对未来负荷波动的模拟效果也就越好。
设待预测日t时刻的确定性预测结果为。对于每一时刻点而言,根据其所处的时段和负荷层次全段选择对应的概率密度分布。设定显著性水平α,由式(7)确定1-α的置信水平下的误差区间[emin,emax]

因为概率密度分布为离散的,无法由式(7)直接得到准确的误差区间,可采用线性差值的办法解得近似的emin和emax。
对于每个时刻都可以计算出置信水平α下的相对误差区间[ ]emin,emax。于是对于t时刻负荷的概率补偿预测置信区间为

遍历所有的时刻点便可以得到每个时刻点对应的概率补偿预测置信区间。将所有时刻点的概率补偿置信区间的下限和上限分别连接,形成上下2条包络线。包络线中的区域即在α置信水平下的负荷可能出现的区域。
2 算例研究
以某大区电网夏季负荷为例进行算例研究。夏季的负荷受气象因素影响大,波动幅度较大,相比其他季节的负荷规律性更较弱,因此如果能够确立该电网夏季负荷的误差分布特性,对于该电网全年的概率补偿负荷预测是十分有帮助的。为了保证足够多的历史样本,选取该电网2014年6、7月的负荷数据,负荷采集形式是每天96点。6、7月份2个月的历史负荷如图2所示。

图2 某大区电网6月1日—7月31日历史负荷层次划分
根据该电网的负荷曲线特性可知,可将一天的负荷划分为明显的4个时段:夜间低谷、早高峰、晚高峰和其他时段;负荷水平划分设定为4个负荷区间。按照每个时段内各负荷水平区间的样本点数相等的原则划分的结果如图2所示,其中Dkt代表第k时段、第j负荷层次区域。
按照1.2节所描述的方法分别求得每个区段的离散概率分布函数。以第一个时段为例,4个不同负荷区间的误差概率分布如图3所示。

图3 低谷时段误差概率分布
由图3可以看到,各个负荷区段的误差概率分布相似,都呈现期望为0的近似正态分布的态势。但随着负荷水平层次的增加,误差概率分布图像呈现出向“高瘦”方向发展的趋势:即负荷水平越高,则误差分布越集中,方差越小;而在负荷水平较低的阶段误差分布较为分散,方差较大。因此图3体现了负荷水平越低则误差波动越大的结论。
选取与6、7月份负荷相似度高的8月份作为样本进行误差统计规律的校验。利用式(6)的方法求得误差概率分布的相关性检验结果,如表1所示。
表1的误差概率分布相关性检验结果显示了误差概率分布的规律性强弱。从时段来讲,早高峰的相关系数整体较高,各个负荷水平区段的相关系数均在0.75以上,最高达可达0.92;平段的相关系数整体较低,最高仅0.74。从负荷水平区段来讲,各个时段的相关系数随着负荷水平的发展呈现由低到高再到低的发展趋势,其中第3个负荷水平段的相关系数最高。因此根据误差概率分布相关性检验的结果,早高峰以及中高负荷段的误差分布规律性更强,误差概率性补偿预测的结果可信度更高。
以该大区电网8月15日的预测为例,进行概率性补偿预测修正。采用的传统确定性预测方法模式识别法,预测步骤如下:
(1)映射库训练。首先对历史相关因素(日类型、气温、湿度等)进行映射库训练,得到相关因素的量化映射结果。

表1 误差概率性分布相关性检验结果
(2)相似度计算。计算过去一个月内每天的相关因素与待预测日的相关因素的预报值的相似度,相似度按照式(9)计算

式中:xik代表第i天的第k种相关因素量化值,rij代表第i天和第j天的相似度。设待预测日为第0天,分别求取历史各日与待预测日的相似度r01,r02,…,r0N,N为最大历史天数。
(3)相似度加权平均预测。历史日第j天与待预测日的相似度权重为

式中:Pk,t代表历史第k天t时刻的负荷;P0,t代表待预测日t时刻的负荷;N为最大历史天数。
模式识别法预测结果如图4所示。取置信水平1-α=0.8,根据前文所分析的误差概率统计规律,结合式(7)、式(8)所示的方法逐点计算误差概率补偿预测置信区间。为了直观的体现各点的误差概率补偿情况,将各时刻点的误差区间上限和下限用散点图表示,如图4所示。

图4 8月15日全网负荷误差概率补偿修正预测结果
图4中标注出了实际负荷曲线、预测负荷曲线以及误差概率补偿区间上下限连接形成的包络线。可以看到,以预测曲线为中心,上下2条包络线中的区域就是一定置信水平下负荷的所有误差概率补偿预测的区域,已经包含了负荷发展的所有可能性,实际负荷是贯穿与概率性预测区域诸多可能中的一条曲线。从概率补偿预测的区间来看,峰谷段的区间较大,这与峰谷段的预测准确率较低相吻合;而在平段或者曲线坡度较高处的概率区间较小,则这个时间段的负荷预测相对较为容易,与日常的工作经验也相符合。因此一方面概率性修正预测结果满足了不确定性风险决策的要求,另一方面在实际工作中也可能指导工作人员根据确定性预测结果和概率置信区间的排列,结合实际情况对预测结果做出合理可信的修正,提高预测质量。
3 结论
本文研究内容主要解决了现行预测模式中存在的2个问题,即历史预测误差的信息利用和不确定性的要求,提出了基于预测误差概率分布特性统计基础上概率性补偿预测办法。对误差概率特性分布统计依据时段、负荷水平区间,遵循样本点数相等的原则进行划分,得到详细的误差离散概率分布。对误差概率分布进行相关检验,确定出误差分布规律最强的时段和负荷水平。在此基础上对确定性负荷预测结果进行概率性补偿预测,得到逐点的概率预测置信区间。最后以某大区电网夏季负荷为例,研究了其负荷概率分布特性,通过计算得到了该电网的夏季的日负荷概率性补偿修正预测结果,并阐明了补偿结果的意义。
本文提出的概率补偿预测办法相比常规预测办法采取了更加严格的数学统计的思想,得到了满足精细化要求的概率性预测结果,但同时在误差概率分布的统计方面还存在理想化假设带来的确定性。比如:待预测日的负荷情况必须在误差概率分布的统计方式所选取的历史样本集合之内,否则所得到的分布特性不具备较好的演绎和预测能力;在误差较大而分布规律性差的地区和季节也存在不相适应的问题,有待后续进一步的研究。
[1] 张涛.电力系统短期负荷预测技术的研究与应用[D].杭州:浙江大学,2005.
[2] 杨文佳,康重庆,夏清,等.基于预测误差分布特性统计分析的概率性短期负荷预测[J].电力系统自动化,2006,30(19):47-52.
[3] 周建中,张亚超,李清清,等.基于动态自适应径向基函数网络的概率性短期负荷预测[J].电网技术,2010,34(3):37-41.
[4] 陈国栋,姚建刚,钱卫华,等.基于误差预测修正的负荷预测研究[J].现代电力,2007,24(3):11-15.
[5] Wang Y,Xia Q,Kang C.Secondary forecasting based on deviation analysis for short-term load forecasting[J].Power Systems,IEEE Transactions on,2011,26(2):500-507.
[6] LI Y,FANG T,YU E.Study of support vector machines for short-term load forecasting[J].Proceedings of the Csee,2003,23(6):55-59.
[7] Moghram I,Rahman S.Analysis and evaluation of five short-term load forecasting techniques[J].Power Systems,IEEE Transactions on,1989,4(4):1 484-1 491.
[8] 赵冬梅,魏娟,张旭,等.基于相似日的超短期母线负荷概率性区间预测[J].电气应用,2013,32(11):36-40.
[9] 王景芝,张婷婷,黎平,等.一种计及横向误差校正的短期负荷预测方法[J].东北电力大学学报:自然科学版,2008,28(1):21-26.
[10] 黄梅,杨少兵.负荷建模中的负荷调查统计分类[J].电网技术,2007,31(4):65-68.

