基于模糊综合评价法的土地储备风险评估

马可，许亚东，朱家明

(安徽财经大学a.国贸学院，b.经济学院，c.统计与应用数学学院，安徽蚌埠233030)

基于模糊综合评价法的土地储备风险评估

马可a，许亚东b，朱家明c*

(安徽财经大学a.国贸学院，b.经济学院，c.统计与应用数学学院，安徽蚌埠233030)

针对土地储备项目的风险评估，通过主成分判别、层次分析、模糊综合评价、残差分析、系统聚类分析等方法，运用MATLAB、EXCEL等软件，综合分析土地储备项目指标数据和风险之间的关系，依托模糊综合评价模型，给出风险评估方法，并与专家综合评价打分做对比验证，证明了本文给出的风险评估方法具有很高的可信度，适合对土地储备部门分析项目风险提供参考.

土地储备;模糊综合评价;残差分析;模糊C均值聚类;MATLAB;Eviews①

0 引言

伴随经济快速的发展，我国土地资源日益减少而其使用价值则逐年增加，土地储备机构积极管理各类土地储备项目，在增加各地财政收入的同时以改善基础设施建设.由于土地储备项目存在各类风险，若处理不当，可能会给地方经济带来重大损失，甚至引发区域金融风暴.因此，实用的风险评估方法将成为解决此类问题的关键，且对合理选择开发项目、充分利用土地资源、获取更大效益均具有重要意义，本文试图建模对土地储备风险进行定量评估，以给出有价值的结论.

1 数据的获取及假设

数据来源于2014第七届“认证杯”数学建模网络挑战赛C［1］.为便于解决问题，提出以下假设:⑴土地储备方案实行期间无重大自然灾害，不考虑其他因素影响;⑵所选取的社会经济指标能基本涵盖风险评估的重要方面;⑶方案实行期间没有发生严重的通货膨胀和通货紧缩，社会较稳定;⑷所给数据只有个别漏填或误填现象，其余数据可以充分反映真实信息;⑸所采用的指标，不会全部同比例变化;⑹存在人为修改的数据，修改幅度较大.

2 土地储备方案的风险评估方法

2.1 研究思路

首先确定影响风险评价各项指标，采用主成分分析法并结合相关数据、相应理论，根据贡献率大小确定影响项目风险评价指标.其次确定各个主成分的权重，采用层次分析法，通过建立风险递阶层次结构图并结合相关数据，确立合理的权重.最后进行风险评估，采用相对偏差模糊矩阵评价法，建立模糊综合评价模型，得到项目风险度的函数公式.

2.2 数据处理

在此根据相关数据，利用主成分分析法［2］，运用MATLAB软件，根据贡献率大小确定了影响项目风险评价的4个指标，分别为财务净现值率(项目财务净现值与项目总投资之比)、融资成功率(银行批复额度与项目投资总额预算之比)、资金动态回收周期和人口密度相对数.在此基础上，采用层次分析法，首先建立风险递阶层次结构图，并采用定量相对重要度a=1.618的新模糊标度，得到模糊判断矩阵如下:

其次，利用特征向量法寻找出四个因素的权重向量，运用MATLAB软件，得到各指标权重分别为:W=(0.466，0.288，0.178，0.068).

最后为了保证结果的有效性，对其进行一致性检验，得到判断矩阵的最大特征值为: λmax=4以及一致性指标CI=9.3411×10-7，当n=4时，查询随机一致性指标表可知RI =0.94，经计算可知CR=9.9373×10-7＜0.1，则比较判断矩阵通过一致性检验［3］并得到各指标权重(见表1).

表1 各评价指标权重

2.3研究方法

对项目进行风险评估时，采用相对偏差模糊矩阵评价［4］进行分析求解.

2.4 结果分析

由上述模糊综合评价方法，利用EXCEL软件对数据进行处理，可得到相对偏差模糊矩阵.

最后结合层次分析法中所求出的权重，可得到项目风险度公式为:

Yi=0.466×ri1+0.288×ri2+0.178×ri3+0.068×ri4(3)

3 退回项目的风险分析

3.1研究思路

考虑到方案数据存在人为修改的可能，采用残差分析法对各个指标的数据进行分析，找出置信带以外的异常数据对应的项目，其次按照前述的风险评估方法得出风险度，并选出10个风险最大的项目，最后从风险评估模型的角度，对选出的10个项目进行风险分析.

3.2 研究方法

对项目进行风险分析时，需要考虑数据人为修改的风险，故进行数据残差分析，做出评价指标与风险度的函数模型，找出分散在置信带以外的数据即异常数据.首先用Eviews做出财务净现值率、融资成功率、人口密度相对数和动态回收周期与风险度的相关图，可知融资成功率和人口密度相对数与风险度的相关图比较分散，舍弃这两项指标不做分析，对财务净现值率和动态回收周期与风险度之间进行函数拟合.

首先对财务净现值率与风险度进行分析，运用多种模型进行曲线拟合，最终得到风险度与财务净现值率的指数函数为:log(Yi)=-1.9916+1.7798×ai1，并且得到R2=0.914973，拟合结果较好，于是对财务净现值率与风险度进行残差分析，得到相应的残差图(如图1)，由残差分析表可知异常数据的项目编号为:1、4、6、20、22、38、46、47、48、56、57、69、71.

图1 财务净现值率的残差分析图

图2 项目风险贡献率

同理，对动态回收周期与风险度进行分析时，得到风险度与动态回收周期的线性函数为:

Yi=0.2078+0.6244×ai2(4)

进行残差分析得到相应的残差分析图，并由残差分析表可知异常数据的项目编号为:2、4、38、46、47、48、49、56、57、69、71.

3.3 结果分析

按前述风险评估，运用EXCEL得出各个项目对应的风险度，并对此进行分析可知10个风险较大的项目编号为:4、47、24、2、69、36、71、46、51、62.并与残差分析结果对照，可知10个风险较大的项目与可能有人为修改的项目间存在部分重合，在一定程度上也可说明前述中的风险评估方法具有一定的可行性.结合上述分析结果可知，编号为4、46、47、69、71的项目风险较大的原因:可能为财务净现值率以及动态回收周期存在人为修改;编号为2的项目风险较大的原因:可能为动态回收周期存在人为修改的可能性.

现利用前述风险评估方法，从风险评价指标的角度对各项目进行风险分析，在此定义各评价指标的风险度贡献率为:

其中fij为风险率贡献率.根据项目各指标相应风险度贡献率，运用EXCEL软件做出所选10项目各指标风险贡献率图(如图2).由下图可知:在10个风险较大的项目中，总体上人口密度相对数对项目风险几乎无影响，财务净现值率对项目风险的贡献率最大即为项目存在的最大风险，其次是动态回收周期，最后是融资成功率.

综上所述，项目风险较大的原因除了存在人为修改可能之外，还有可能与各评价指标的综合影响有关.得到编号为46项目风险较大原因:除了财务净现值率以及动态回收周期存在人为修改可能，融资成功率较低，人口密度相对数较大;编号为4、47、69、71项目风险较大原因:除了财务净现值率以及动态回收周期存在人为修改可能，融资成功率较低;编号为2项目风险较大原因:除了动态回收周期存在人为修改可能，财务净现值率较低，融资成功率较低;编号为24、36项目风险较大原因:财务净现值率较低，动态回收周期较短，融资成功率较低，人口密度相对数较大;编号为51、62项目风险较大原因可能为:财务净现值率较低，动态回收周期较短，融资成功率较低.

4 风险评估方法的进一步修正

4.1 研究思路

首先对专家评分数据进行处理，采用指标均值对缺失数据进行分析及填补，采用聚类分析对数据进行异常值分析并处理，得到项目的综合评价得分，其次综合考虑项目的收益与风险，在项目的收益方面选取相关指标进行主成分分析，找出对项目风险评估的第5个准则并计算各项评价指标的权重.最后建立相对偏差模糊综合矩阵模型求解项目风险度，并与专家评估结果进行拟合，从而构建新的项目风险评估函数.

4.2 数据处理

针对专家评分结果，易知项目序号为26的监察部评分以及序号为69的财务部评分存在缺失，此处采用各部门评分均值填补缺失数据，项目26缺失数据填补为6，项目69缺失数据填补为8.

针对可能存在的异常数据，采用聚类分析，运用SPSS软件做出项目聚类结果的树状图［5］.由图可知，项目47的数据异常，可能为观测员误填现象.对所有项目对应的五个评分数据分别进行数据分析可知，储备部门平均打分为7.7972，标准差为0.9213，而项目47的储备部评分为2分，严重偏离总体评分，在此以该列指标数据均值代替原数据，得到项目47的储备部评分为8分.

4.3 研究方法

采用变异系数法综合分析各部门专家对74项项目的评分结果，得到各部门评分所占权重分别为:ω1=0.2443，ω2=0.1459，ω3=0.1347，ω4=0.2191，ω5=0.2560，并得到综合评价得分模型:Gi=0.2443gi1+0.1456gi2+0.1347gi3+0.2191gi4+0.256gi5(6)

利用该模型得到各个项目的综合评价得分.

通过与各部门专家综合评分结果对比分析，发现模型结果与专家评分结果存在一定出入，在分析项目风险度时，考虑项目收益类指标，在此对项目的有关财务类指标进行主成分分析，即财务净现值、项目投资总额估算(万元)，自有资金，银行批复额度等因素，运用MATLAB软件进行运算，根据贡献率大小，取第一主成分进行分析，并将其命名为收益补偿风险值，相应表达式如下:

Fc()x=0.2304x1+0.2038x2+0.1932x3+0.2341x4(7)

其中x1为财务净现值，x2为项目投资总额估算，x3为银行批复额度，x4为自有资金.

由此得到评估风险度新指标分别为收益补偿率(收益补偿风险值与项目预期收益之比)、融资成功率、动态回收周期、财务净现值率和人口密度相对数，利用层次分析法求解各指标权重大小，运用MATLAB软件得到各个评级指标权重如下:

表2 各评价指标权重

随后对其进行一致性检验，可知λmax=5.088，一致性指标CI=0.022，一致性比例CR=0.02＜0.1，认为比较判断矩阵一致性可以接受.

4.4 结果分析

在得出权重基础上，利用相对偏差模糊矩阵评价方法，得到各项目新的综合评价风险度公式为:Yi=0.539ri1+0.212ri2+0.121ri3+0.082ri4+0.045ri5，并运用EXCEL求解得到各项目风险度(见表3).

运用Eviews对前述得到的项目风险度与专家得分进行函数拟合，得到相应对数函数:

log(y)=1.7752-0.2506×log(x)，R2=0.834175(8)

其中y为专家综合得分，x为项目风险度，F=362.1934，由上述结果可知，函数拟合效果较好，并且通过了F检验，可以用来近似代替专家对项目进行评估量分.

表3 项目风险度表

5 评价指标变化范围

5.1 研究思路

首先利用模糊C均值聚类模型，得出74个项目聚类中心及隶属度矩阵，在此基础上将74个项目进行分类，进而分析不同类别项目的各项指标值，建立财务内部收益率、融资成功率、动态回收周期以及收益补偿风险值对项目综合评价的线性回归模型.其次针对某类项目一个评级指标，利用控制变量法对其余各项评价指标取平均值固定，推倒出针对此类项目不同评级指标对应的迭代方程，最后综合考虑各类项目的各指标变化范围，得出各评价指标的允许变化范围.

5.2研究方法

运用模糊C均值聚类［6］进行分类，目标函数相应如下:

其中J(U，V)表示了各类中样本到聚类中心的加权距离平方和，权重是样本xk对第i类隶属度的m次方，聚类准则取求解的极小值:(min){J(U，V)}其中聚类中心为:

5.3 结果分析

(1)对各项目进行分类

基于上述理论，运用MATLAB软件，得出聚类中心及隶属度矩阵，并在隶属度矩阵的基础上，通过相应程序对各个项目进行了分类，得到结果(见表4)

表4 各类别项目表

(2)针对第五类项目各指标的多元回归分析

首先做出各评级指标值与评价得分的散点图，由于人口密度相对数数值较小，散点图较分散而且对项目风险度的影响较小，故此不对该指标进行分析，通过其他指标散点图发现内部收益率、融资成功率、动态回收周期以及收益补偿风险率与综合评价得分之间存在一定的线性相关性，因而在此基础上建立多元线性回归模型:

y=β0+β1x1+β2x2+β3x3+β4x4+ε(11)

β0、β1、β2、β3、β4为回归系数，ε为随机误差.利用Matlab软件，对该模型进行不断改进，剔除异常点，进行多次回归并得到残差分析图(如图3).

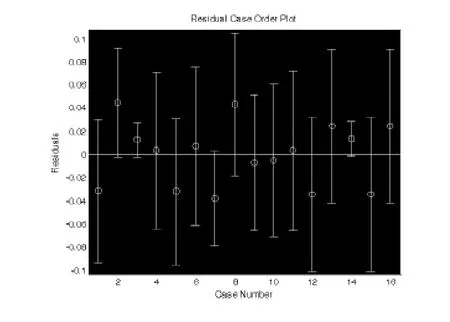
图3 残差分析图

由相应的运行结果可知，所有回归系数置信区间中均未含有零点，R2=0.9831模型拟合程度较高，得到回归模型为:

最后对回归模型进行残差的正态性检验:由jbtest检验，h=0表明残差服从正态分布，进而由t检验可知h=0，p=1，故残差服从均值为零的正态分布［7］.

(3)指标变化范围

利用第五类项目回归方程，首先针对该类项目财务净现值率范围，运用控制变量法进行求解，求解步骤如下:

其中l1表示第五类项目财务净现值率允许变化幅度，由上述模型得到第五类项目各评价指标的变化范围(见表5).

表5 第五类项目各项评价指标中间值以及变化范围

同理，运用上述建模方法得到第一类、第二类、第三类以及第四类项目的评价指标变化范围，最后汇总得出整个项目的评价指标允许变化范围(见表6).

表6 各指标允许变化范围

6 总结

针对4个有关土地储备项目风险问题，运用多种分析方法建立模型进行相关研究，随着研究的深入以及专家评分的帮助，对项目的风险评估方法得到了进一步完善，建立的风险评估模型充分考虑到了各种风险影响因素，可在一定程度上替代专家评估作用，在得到的评价指标允许变化范围内，具有较强的应用性和推广性;本文运用多种软件给出各种相关图形，使人对数据的处理、模型的分析、结果的得出更形象易懂.文中的风险评估模型，能够对项目的风险进行一定的估算，可以为土地储备部门提供一定的参考.

［1］2014年第七届“认证杯”数学中国数学建模网络挑战赛C题.http://www.tzmcm.cn/.

［2］周菲，赵婧婧.基于主成分分析的安徽省经济增长质量研究［J］.枣庄学院学报，2013.30(5):113-117.

［3］张圣勤.MATLAB7.0使用教程［M］.北京:机械工业出版社，2006.

［4］杨桂元，黄己立.数学建模［M］.合肥:中国科学技术大学出版社，2008.

［5］薛微.统计分析与SPSS应用［M］.北京:中国人民大学出版社，2009.

［6］王晓敏.江苏省旅游业竞争力研究［J］.枣庄学院学报，2014.31(2):132-136.

［7］吴礼斌，闫云侠.经济数学实验与建模［M］.天津:天津教育出版社，2009.8，218-219.

［责任编辑:闫昕］

Based on the Fuzzy Comprehensive Evaluation Method of Land Reserve Risk Assessment

MA Kea，XU Ya-dongb，ZHU Jia-mingc
(Anhui University of Finance and Economics a.School of international economic and trade，b.School of Statistics and Appl.Math，c.School of economics，Bengbu 233030，China.)

In view of the land reserve project risk assessment，through the principal component method，analytic hierarchy process(ahp)and fuzzy comprehensive evaluation method，the residual analysis，system cluster analysis and a series of methods，by use of MATLAB and EXCEL software，comprehensive analysis of the land reserve project index data，and the relationship between the risk，based on a fuzzy comprehensive evaluation model of risk assessment methods are given，and compared with expert grade comprehensive evaluation do validation，proved in this paper the risk assessment method has a high reliability，suitable for project risk analysis of land reserve department to provide the reference.

land reserve;fuzzy comprehensive evaluation;residual analysis;the fuzzy c-means clustering;matlab;eviews

F301

A

1004-7077(2015)02-0107-07

2015-01-05

国家自然科学基金(项目编号:11301001);安徽省大学生创新项目(项目编号:AH201410378349);安徽财经大学教研项目(项目编号:acjyzd201429).

朱家明(1973-)，男，安徽泗县人，安徽财经大学统计与应用数学学院副教授，硕士，主要从事应用数学的研究.