天目山近自然毛竹林空间结构与胸径的关系

仇建习, 汤孟平,2,*, 沈利芬, 娄明华, 庞春梅

1 浙江农林大学环境与资源学院, 临安 311300 2 浙江省森林生态系统碳循环与固碳减排重点实验室, 临安 311300 3 天目山国家级自然保护区管理局, 临安 311300

天目山近自然毛竹林空间结构与胸径的关系

仇建习1, 汤孟平1,2,*, 沈利芬1, 娄明华1, 庞春梅3

1 浙江农林大学环境与资源学院, 临安 311300 2 浙江省森林生态系统碳循环与固碳减排重点实验室, 临安 311300 3 天目山国家级自然保护区管理局, 临安 311300

以浙江省天目山国家级自然保护区内的近自然毛竹林为研究对象，设置1块100m×100m的固定标准地，采用相邻网格调查法划分为100个调查单元，通过全站仪精确定位毛竹基部的三维坐标(X,Y,Z)，利用角尺度、大小比数和年龄隔离度3个林分空间结构指数，并按毛竹胸径大小划分为Ⅰ(DBH<7cm) 、Ⅱ(7cm≤DBH<13cm)、Ⅲ(DBH≥13cm)3个径级，分析近自然毛竹林空间结构与胸径的关系。结果表明：毛竹林直径结构呈右偏近似正态分布，与乔木同龄林直径结构较接近；Ⅰ、Ⅱ、Ⅲ径级毛竹以及全林分的空间分布格局分别为聚集、随机、随机和随机，毛竹林角尺度随径阶的增加有减小的趋势，且服从幂函数关系，决定系数R2=0.7793，各径阶角尺度无显著性差异(P>0.05)；毛竹林整体处于中庸状态，胸径大小分化不明显，各径级毛竹优势度排序为Ⅲ>Ⅱ>Ⅰ，毛竹林大小比数随径阶的增加而减小，与胸径呈线性关系，决定系数R2=0.9233，各径阶大小比数差异极显著(P<0.01)；毛竹林的平均年龄隔离度为0.8178，属强度至极强度异龄，各径级毛竹年龄隔离程度大小排序为Ⅲ>Ⅱ>Ⅰ，毛竹林年龄隔离度随径阶的增大呈现逐渐递增的趋势，且服从幂函数关系，决定系数R2=0.6774，各径阶年龄隔离度差异极显著(P<0.01)。

毛竹林; 空间结构; 胸径; 角尺度; 大小比数; 年龄隔离度

直径结构是最基本、最重要的林分结构[1- 2]。由于直径结构比较容易精确测定且与林分密度[3]、年龄[4- 5]、树高[6]、冠幅[7]以及生物多样性[8]等因子存在密切关系，因此林分直径结构常用于直接反映林分结构特征[8- 9]。直径结构属于非空间结构，多用于分析乔木林的结构与生长的关系，如Rubin等[4]通过对阔叶林研究，认为直径分布规律可揭示现有林分小径级林木在末来是否可以取代当前林分的大径级林木，并评估林分永续性的潜力。近年来，森林空间结构研究呈日益增长趋势，直径结构作为反映生长的因子，常用于分析林分空间结构与直径结构的关系。闫东峰等[10]将不同径级代替龄级结构，分析宝天曼国家级自然保护区栎类天然林不同龄级林分空间特征。徐海等[11]采用大小比数、角尺度和混交度等3个指数，分析了不同径阶天然红松阔叶混交林的空间结构特征。同样，对毛竹(Phyllostachysedulis)林而言，直径结构是反映生长的重要结构[12]。毛竹胸径大小直接影响立竹叶面积和根系面积数量，从而影响毛竹的生长[12]。学者们已在毛竹胸径与竹高、竹枝下高、冠幅、立竹度、年龄组成等关系方面做了大量研究[3,5- 6]。但是，这些因子均属于非空间结构。近年的研究表明，与距离有关的空间结构指数可以精确描述毛竹林的结构特征，对分析和调控毛竹林结构与功能关系至关重要[13- 14]。然而，在毛竹林空间结构与胸径的关系方面的研究尚少见报道。

林分空间结构主要通过混交度、大小分化度和空间分布格局3个方面进行分析[15- 16]。混交度是描述林分树种相互隔离程度的指数[17- 18]；大小分化度是用于反映林木的生长优势(非均一性)[17]；空间分布格局是指林木个体在水平空间的分布形式[16,19]。本研究以浙江省天目山国家级自然保护区的近自然毛竹林为对象，采用混交度、大小分化度和空间分布格局3个空间结构指数，通过将不同胸径毛竹划分为3个径级，分析近自然毛竹林空间结构与胸径的关系，旨在为毛竹林可持续经营提供理论依据。

1 研究区概况

浙江省天目山国家级自然保护区素以“大树华盖闻九州”而闻名，该自然保护区位于浙江省西北部临安市境内(119°23′47″—119°28′27″E 30°18′30″—30°24′55″N)，总面积1050hm2，主峰海拔1506m。年平均气温8.8—14.8℃，≥10℃年积温2500—5100℃。年降水量1390—1870mm，相对湿度76%—81%。温润多雨的气候特点非常适合植物的生长繁衍，森林植被覆盖率高达95%，天目山拥有世界罕见的柳杉群落。近自然毛竹林作为一种特殊的森林植被类型，主要分布于在海拔350—900m。毛竹林立地条件和林内环境的相互作用，造成林下植被生物多样性较低[20]。主要有豹皮樟(Litseacoreanavarsinensis)、短尾柯(Lithocarpusbrevicaudatus)、微毛柃(Euryahebeclados)、细叶青冈(Cyclobalanopsismyrsinaefolia)、连蕊茶(Cameliafraterna)、马银花(Rhododendronovatum)和牛鼻栓(Fortuneariasinensis)等。

2 研究方法

2.1 固定标准地调查

在浙江省天目山国家级自然保护区的近自然毛竹林设置1块100m×100m的固定标准地，标准地中心海拔840m，主坡向南偏东30°。采用相邻网格法，将固定标准地划分为100个10m×10m的调查单元(图1)。在每个调查单元中，对每棵活立竹进行每木检尺，主要调查其胸径、年龄、竹高、枝下高、冠幅、弯曲状态等因子，用南方全站仪NTS355对样地内每棵毛竹进行精确定位，确定毛竹基部的三维坐标(X,Y,Z)位置(图2)。采用观杆法、枝痕法和号竹法判定毛竹年龄[12]。

图1 标准地网格图

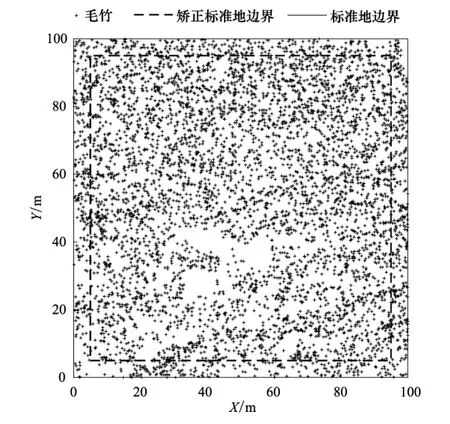
图2 标准地立竹定位

2.2 边缘校正

为消除标准地边缘效应，使用距离缓冲区的方法进行边缘校正。在标准地内的四条边界线的内侧设置宽度为5m的带状缓冲区。缓冲区以内为90m×90m的矫正标准地(图2)。在计算空间结构指数时，仅将矫正标准地内毛竹作为对象竹，竞争竹则为标准地中所有活立竹。

2.3 毛竹林空间结构单元

空间结构单元是分析毛竹林空间结构的基础，它是由对象竹和最近的n株相邻竹组成。确定空间结构单元的关键在于选取相邻竹的株数n。惠刚盈等[21]研究指出，n=4可以构成最佳空间结构单元。因此，本研究采用“1对象竹+4相邻竹”的空间结构单元。

2.4 径阶和径级划分

采用上限排外法对毛竹胸径按2cm径阶整化，并根据标准地内毛竹径阶分布的实际情况，把毛竹划分为3个径级，即胸径<7cm为Ⅰ径级，7—12.9cm为Ⅱ径级，≥13cm为Ⅲ径级。

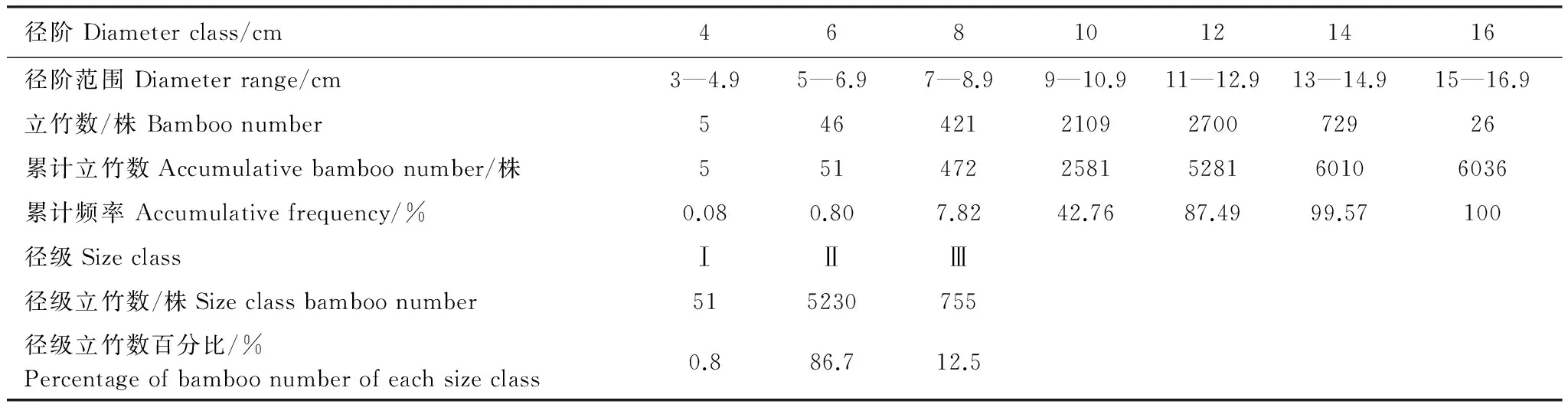
表1 毛竹林分胸径分布Table 1 DBH distribution of Bamboo stand

2.5 角尺度

角尺度通过描述对象木周围最近邻木空间分布均匀性来判定林分空间分布格局。从对象木出发，任意2个最近相邻木的夹角有2个，其中小角为a，大角为β，最近相邻木均匀分布时夹角设为标准角a0(a0=72°)。角尺度是最近相邻木角小于标准角a0的个数占相邻木4株的比例，用公式表示为[22]

(1)

式中,Wi为第i株对象竹角尺度；当第j个a角小于标准角a0时，aij=1，反之，aij=0。Wi取值有以下5种：0(绝对均匀)，0.25(均匀)，0.5(随机)，0.75(不均匀)，1(聚集)。

2.6 大小比数

大小比数是大于对象木的最近相邻木占所考察的4株最近相邻木的比例[15]，所谓大小，可用胸径、树高和冠幅等因子表示。在本研究中采用胸径大小比，公式为[15]

(2)

式中,Ui为第i株对象竹大小比数；相邻竹j胸径大于对象竹i时，Kij=1，反之，Kij=0；Ui的取值有以下5种：0(优势)，0.25(亚优势)，0.5(中庸)，0.75(劣势)，1(绝对劣势)。

2.7 年龄隔离度

混交度被定义为对象木i的4株最近邻木中与对象木不属同种个体所占比例[22]。本研究的对象是近自然毛竹纯林，因此混交度不适用于毛竹纯林的物种隔离度分析。然而，竹年龄是反映毛竹林更新生长的重要因子[12]，是毛竹林结构的重要组成部分[23]。将不同竹龄视为不同种，则混交度可表示不同竹龄的相互隔离程度，简称年龄隔离度[18]。本文将采用Gaodow等[24]提出的混交度计算公式计算年龄隔离度：

(3)

式中,Mi为对象竹i的年龄隔离度；vij为离散变量，当对象竹i与相邻竹j同龄时，vij=0，反之，vij=1。Mi取值有以下5种：0.00(同龄)；0.25(弱度异龄)；0.50(中度异龄)；0.75(强度异龄)；1.00(极强度异龄)。

空间结构指数的分析比较都采用均值，利用高级计算机程序设计语言C#编制计算角尺度、大小比数、年龄隔离度的计算程序。

3 结果与分析

3.1 毛竹林直径结构

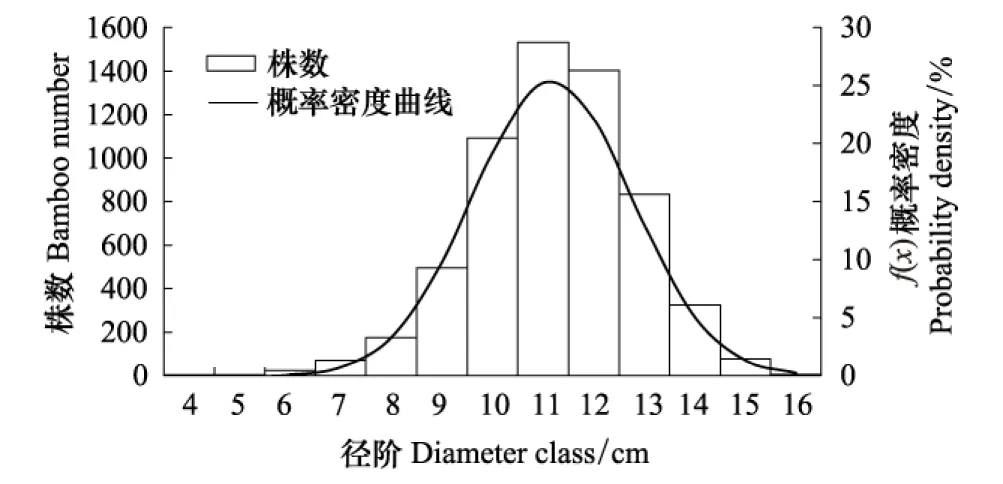
图3 毛竹林直径分布

典型的乔木同龄林株数按胸径的分布呈近似正态分布；而异龄林直径结构则呈现双曲线形式的反J形或负指数分布[1,25]。近自然毛竹林为典型的异龄林，Ⅰ、Ⅱ、Ⅲ径级毛竹分别占0.008%、86.7%、12.5%(表1)，毛竹林分平均直径为11.29cm，毛竹林分直径分布曲线与乔木同龄林接近，近似服从正态分布(图3)。为进一步证明该结论，对标准地内毛竹直径数据进行正态分布假设检验，结果表明：毛竹林直径分布的偏度等于-0.284，说明毛竹林直径结构呈右偏分布；峰值(kurtosis)为0.430，说明毛竹林直径分布曲线比正态分布曲线尖峭。偏度与峰值都接近于0，说明毛竹林直径结构呈右偏近似正态分布。

3.2 角尺度与毛竹胸径的关系

图4 角尺度与对象竹径阶的关系

角尺度可用于描述林分空间分布格局。根据角尺度判别标准[22]，林分空间分布格局有3种：平均角尺度W∈[0.475，0.517]，随机分布；W<0.475，均匀分布；W>0.517，聚集分布。图4为各径阶平均角尺度与其对应径阶(d)的关系图。可见，角尺度随径阶的增加有减小的趋势，且服从幂函数关系，幂函数拟合决定系数R2=0.7793。对不同径阶的角尺度进行单因素方差分析(one-way ANOVA)，结果表明不同径阶毛竹之间的角尺度无显著性差异(P>0.05)。

表2统计了林分和各径级的角尺度平均值及其频率分布，进一步反映了角尺度与胸径的关系。毛竹林平均角尺度0.5131(表2)，说明毛竹林总体上呈随机分布，但位于随机分布状态的下限临界值附近，接近聚集分布。这个结果与兰思仁[26]研究的武夷山天然毛竹林分布格局基本一致。

角尺度与径级的关系：Ⅰ径级毛竹平均角尺度值>0.517，毛竹呈轻度聚集分布；Ⅱ、Ⅲ径级毛竹平均角尺度W∈[0.475，0.517]，毛竹均呈随机分布，但接近聚集分布，与林分的总体分布格局基本一致。各径级Wi=0和Wi=1上分布频率都很低，即处于绝对均匀和聚集这两种状态的结构单元很少；而Wi=0.5时的分布频率最高，分别占各径级结构单元数的46%、59%、58%，其中Ⅱ、Ⅲ径级毛竹中处于随机状态的结构单元数明显多于Ⅰ径级毛竹；各径级Wi=0.75的分布频率分别为33%、17%、17%，即Ⅰ径级毛竹所包含的不均匀结构单元频率明显高于Ⅱ、Ⅲ径级毛竹，这是导致Ⅰ径级毛竹分布状态区别于Ⅱ、Ⅲ的直接原因。

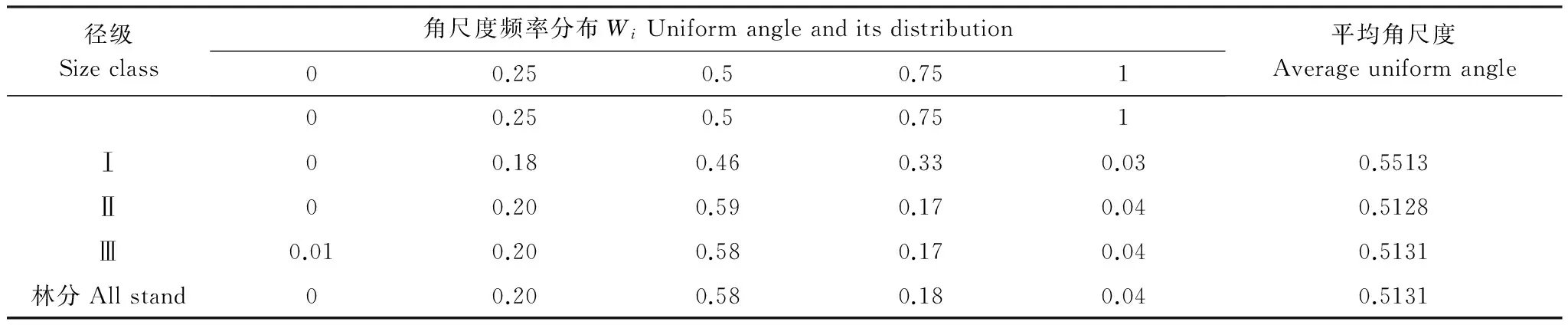
表2 各径级毛竹角尺度及其频率分布Table 2 Uniform angle and its distribution on each size class

3.3 大小比数与毛竹胸径的关系

大小比数描述相邻毛竹之间的差异，反映立竹在林分中的生长优势程度。对某一对象竹而言，大小比数越小，来自周围相邻竹的竞争压力越小，在竞争中越处于有利地位。从表3可见，毛竹林的平均大小比数为0.495，表明林分胸径大小分化不明显，林分基本处于中庸状态。毛竹林大小比数的频率分布呈现出均衡分布的特征，在各状态下的分布频率均在20%左右。

根据各径级毛竹大小比数值可知，各径级优势度排序为Ⅲ>Ⅱ>Ⅰ，Ⅲ径级毛竹明显处于优势地位，Ⅱ径级毛竹处于中庸地位，Ⅰ径级毛竹受压，处于劣态(表3)。Ⅲ径级毛竹Ui=0和Ui=0.25的分布频率较高，说明该径级亚优势和优势的结构单元较多；Ⅰ径级毛竹Ui=1的分布频率最高，达到了92%，因此Ⅰ径级毛竹处于劣势地位；Ⅱ径级毛竹在各状态下的分布频率较为均匀，即Ⅱ径级毛竹中优势、亚优势、中庸、劣势和绝对劣势的毛竹数量大致相当。毛竹林大小比数随径阶(d)的增大而减小，且符合线性关系，两者之间的拟合决定系数高达0.9255(图5)，这个结果与乔木林大小比数和胸径的关系基本一致[11,27]。对不同径阶的大小比数进行单因素方差分析，结果表明不同径阶毛竹之间的大小比数有极显著性差异(P<0.01)。

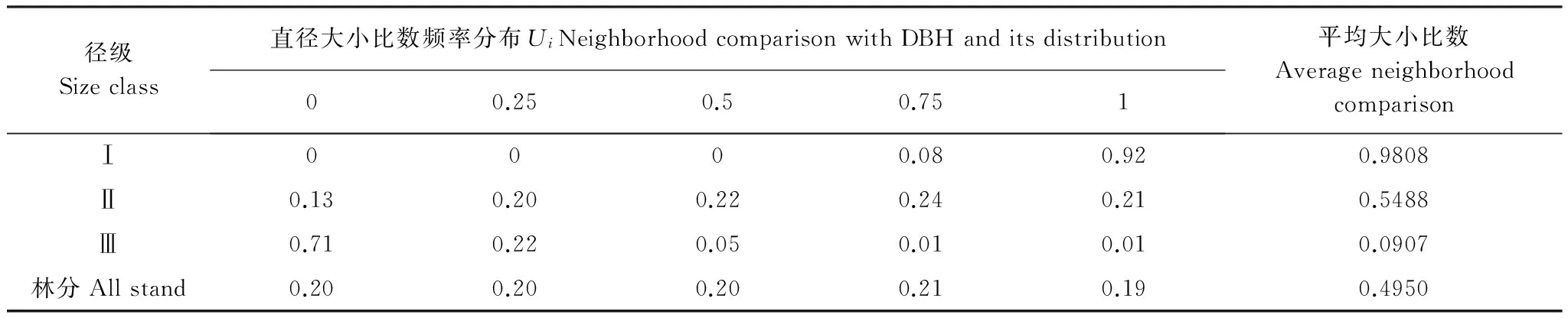
表3 各径级毛竹大小比数及其频率分布Table 3 Neighborhood comparison and its distribution on each size class

图5 大小比数与对象竹径阶的关系

3.4 年龄隔离度与毛竹胸径的关系

毛竹纯林的年龄隔离度反映毛竹林内竹龄多样性及竹龄空间配置情况[14]。由图6可知，毛竹林年龄隔离度随径阶(d)的增大呈现逐渐递增的趋势，且服从幂函数关系，幂函数拟合决定系数R2=0.6774。对不同径阶的年龄隔离度进行单因素方差分析，结果表明不同径阶毛竹之间的年龄隔离度有极显著差异(P<0.01)。

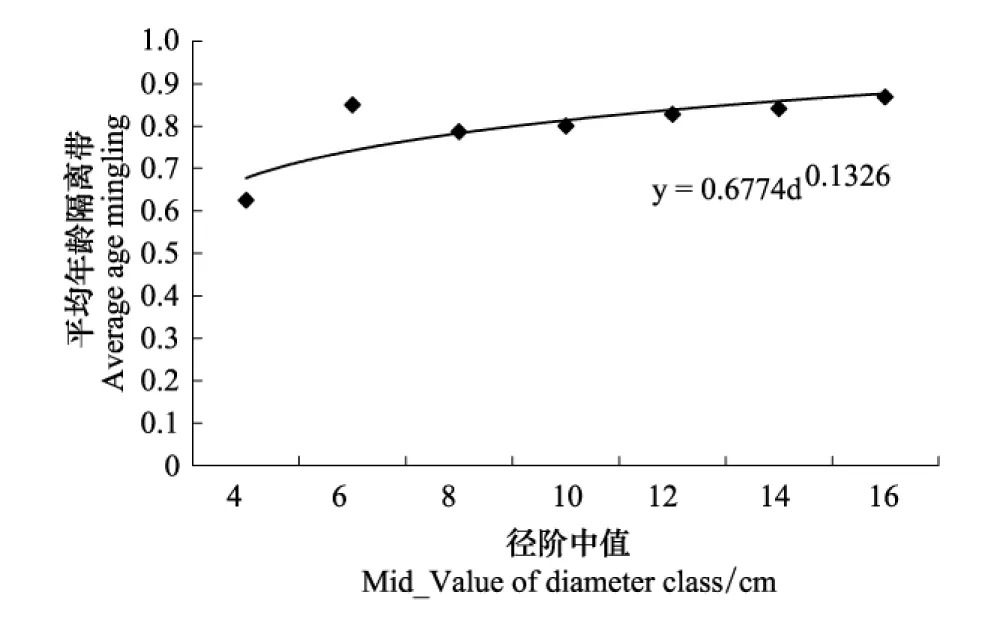
图6 年龄隔离度与对象竹径阶的关系分布

由表4可知，毛竹林的平均年龄隔离度为0.8178，即对象竹的最近4竹相邻竹中与其年龄相同的毛竹不超过1株，属强度至极强度异龄。Ⅰ、Ⅱ、Ⅲ径级毛竹处于强度异龄和极强度异龄状态下的结构单元的频率均为最高，并且各径级平均年龄隔离度都在0.8左右，说明各径级毛竹的年龄隔离程度较高。各径级毛竹年龄隔离程度大小排序为Ⅲ>Ⅱ>Ⅰ，Ⅲ径级毛竹极强度异龄的结构单元所占比例明显高于Ⅰ和Ⅱ径级，是导致Ⅲ径级毛竹平均年龄隔离度值高于Ⅰ和Ⅱ径级的主要原因。各径级毛竹同龄和弱度异龄的结构单元所占比例极低，接近于0。这主要与近自然毛竹林的自然更新方式有关，毛竹具有通过竹鞭的无性繁殖且生长周期短的特点，在毛竹大年形成大量异龄性高的空间结构单元。

4 结论与讨论

(1) 天目山近自然毛竹林的直径结构呈右偏正态分布，与乔木同龄林的直径分布特征相似。聂道平[6]通过对江西大岗山毛竹林的研究得出，毛竹林株数按径阶的分布大多服从weibull分布，但随着林分密度和生产力的提高，会逐渐向正态分布过渡。

(2) 各径级毛竹株数排序为：Ⅱ>Ⅲ>Ⅰ。Ⅱ径级毛竹在数量上占据绝对优势，约占总株数的86.69%，Ⅰ径级毛竹仅占总株数的0.008%。毛竹林平均直径为11.29cm。

(3) 毛竹林平均角尺度为0.513，林分总体上呈随机分布状态，接近聚集分布。这个结果与兰思仁[26]通过采用Taylor幂法则、扩散系数检验、游程检验、中心点四分法检验、点到点距离比率法检验等方法研究的武夷山天然毛竹林分布格局基本一致。但是，本研究发现，不同径级毛竹的空间分布格局存在差异，Ⅰ、Ⅱ、Ⅲ径级毛竹的空间分布格局分别为聚集、随机和随机。各径级毛竹绝对均匀分布和聚集分布的空间结果单元所占比例最低，随机分布的空间结构单元则为最高。毛竹林角尺度随径阶的增加有减小的趋势，且服从幂函数关系，幂函数拟合决定系数R2=0.7793。各径阶毛竹之间角尺度无显著性差异。

(4) 毛竹林的平均大小比数为0.495，表明林分胸径大小分化不明显，林分基本处于中庸状态。毛竹林大小比数的频率分布呈现出均衡分布的特征，在各状态下的分布频率均在20%左右。根据各径级毛竹大小比数取值可知，毛竹林各径级优势度排序为Ⅲ>Ⅱ>Ⅰ，Ⅲ径级毛竹明显处于优势地位，Ⅱ径级毛竹处于中庸地位，Ⅰ径级毛竹处于劣势地位。随着毛竹胸径的增大，毛竹林的大小比数迅速减小。毛竹林胸径与大小比数有线性关系，两者的拟合决定系数高达0.9255，这个结果与乔木林大小比数和胸径关系基本一致[11,27]。各径阶毛竹之间的大小比数有极显著性差异。

表4 各径级毛竹年龄隔离度及其频率分布Table 4 Age mingling and its distribution on each size class

(5) 毛竹林分平均年龄隔离度为0.8178，说明毛竹林的年龄多样性及年龄隔离程度较高。年龄隔离度随径级的增加而增大，各径级均属于强度至极强度异龄。近自然毛竹林无性繁殖方式和生长周期短的特点，促使毛竹林在毛竹大年形成大量的异龄空间结构单元，这从各径级毛竹以及全林分零度混交和弱度混交的结构单元所占比例接近0得到证实。毛竹林年龄隔离度随径阶的增大呈逐渐升高的趋势，且服从幂函数关系，决定系数R2=0.6774。各径阶毛竹之间年龄隔离度有极显著性差异。

系统结构决定其功能。毛竹林的结构在一定程度上决定了其稳定性、发展的可能性与经营空间的大小[28]。传统的毛竹林经营通过调整毛竹林的整齐度、立竹度以及年龄结构等林分因子来改善林分结构[12,23,29]，这些因子由于缺乏空间信息，很难对林分的整体特征作出准确判断。本研究采用的角尺度、大小比数及年龄隔离度是与立竹空间位置有关的空间结构指数，结合毛竹林的非空间因子直径结构，研究表明小径级毛竹的聚集程度较高，年龄隔离程度最低，且竞争压力最大，说明在毛竹林经营管理过程中，可适当的对小径级毛竹进行择伐，但是如何择伐，或许可通过建立类似于乔木林的空间结构优化调控模型[29]，实现精确地选取择伐对象竹的目标，这一问题有待进一步研究。

[1] 孟宪宇. 测树学(第三版). 北京: 中国林业出版社, 2006.

[2] 谢小魁, 苏东凯, 刘正刚, 于大炮, 周莉, 代力民. 长白山原始阔叶红松林径级结构模拟. 生态学杂志, 2010, 29(8): 1477- 1481.

[3] 何东进, 洪伟, 吴承祯. 毛竹林林分平均胸径模拟预测模型的研究. 林业科学, 2000, 36(1): 148- 153.

[4] Rubin B D, Manion P D, Faber-Langendoen D. Diameter distributions and structural sustainability in forests. Forest Ecology and Management, 2005, 222(1/3): 427- 438.

[5] 周国模, 刘恩斌, 刘安兴, 周宇峰. Weibull 分布参数辨识改进及对浙江毛竹林胸径年龄分布的测度. 生态学报, 2006, 26(9): 2918- 2926.

[6] 聂道平. 毛竹林结构的动态特性. 林业科学, 1994, 30(3): 201- 208.

[7] 符利勇, 孙华, 张会儒, 雷向东, 雷渊才, 唐守正. 不同郁闭度下胸高直径对杉木冠幅特征因子的影响. 生态学报, 2013, 33(8): 2434- 2443.

[8] Maltamo M, Kangas A, Uuttera J, Torniainen T, Saramäki J. Comparison of percentile based prediction methods and the Weibull distribution in describing the diameter distribution of heterogeneous Scots pine stands. Forest Ecology and Management, 1999, 133(3): 263- 274.

[9] Uuttera J, Maltamo M. Impact of regeneration method on stand structure prior to first thinning. Comparative study North Karelia, Finland vs. Republic of Karelia, Russian Federation. Silva Fennica, 1995, 29(4): 267- 285.

[10] 闫东锋, 吴明作, 杨喜田. 宝天曼国家级自然保护区栎类天然林林分空间结构特征. 东北林业大学学报, 2011, 39(9): 52- 77.

[11] 徐海, 惠刚盈, 胡艳波, 李储山, 林天喜, 张显龙, 吴相菊. 天然红松阔叶林不同径阶林木的空间分布特征分析. 林业科学研究, 2006, 19(6): 687- 691.

[12] 江泽慧. 世界竹藤. 沈阳: 辽宁科学技术出版社, 2002.

[13] 汤孟平, 唐守正, 雷相东, 周国模, 谢志新. 两种混交度的比较分析. 林业资源管理, 2004, (4): 25- 27.

[14] 邓英英, 汤孟平, 徐文兵, 陈永刚, 娄明华, 赵明水. 天目山近自然毛竹纯林的竹秆空间结构特征. 浙江农林大学学报, 2011, 28(2): 173- 179.

[15] 惠刚盈, 克劳斯·冯佳多. 森林空间结构量化分析方法. 北京: 中国科学技术出版社, 2003.

[16] 汤孟平. 森林空间经营理论与实践. 北京: 中国林业出版社, 2007.

[17] 惠刚盈, von Gadow K, Albert M. 一个新的林分空间结构参数—大小比数. 林业科学研究, 1999, 12(1): 1- 6.

[18] 汤孟平, 娄明华, 陈永刚, 徐文兵, 赵明水. 不同混交度指数的比较分析. 林业科学, 2012, 48(8): 46- 53.

[19] Aguirre O, HUI G Y, von Gadow K, Jiménez J. An analysis of spatial forest structure using neighbourhood-based variables. Forest Ecology and Management, 2003, 183(1/3): 137- 145.

[20] 高志勤, 傅懋毅. 不同结构毛竹林下植被物种多样性比较. 浙江林业科技, 2005, 25(4): 1- 5.

[21] 惠刚盈, 胡艳波. 混交林树种空间隔离程度表达方式的研究. 林业科学研究, 2001, 14(1): 23- 27.

[22] 惠刚盈, 李丽, 赵中华, 党普兴. 林木空间分布格局分析方法. 生态学报, 2007, 27(11): 4717- 4728.

[23] 郑郁善, 洪伟. 毛竹林丰产年龄结构模型与应用研究. 林业科学, 1998, 34(3): 32- 39.

[24] von Gadow K, Bredenkamp B. Forest management. Pretoria: Academica., 1992.

[25] 张会儒, 唐守正. 东北天然林可持续经营技术研究. 北京: 中国林业出版社, 2011.

[26] 兰思仁. 武夷山天然毛竹林分布格局的研究. 福建林学院学报, 1995, 15(3): 277- 280.

[27] 史宇, 余新晓, 岳永杰, 王小平, 秦永胜, 陈俊崎. 北京山区天然侧柏林种内竞争研究. 北京林业大学学报, 2008, 30(S2): 36- 40.

[28] 汤孟平, 唐守正, 雷相东, 李希菲. 林分择伐空间结构优化模型研究. 林业科学, 2004, 40(5): 25- 31.

[29] 洪伟, 郑郁善, 邱尔发. 毛竹丰产林密度效应研究. 林业科学, 1998, 34(1): 1- 4.

The relationship between spatial structure and DBH of close-to-naturePhyllostachysedulisstands in Tianmu Mountain

QIU Jianxi1,TANG Mengping1,2,*, SHEN Lifen1,LOU Minghua1, PANG Chunmei3

1SchoolofEnvironmentandResource,ZhejiangAgricultureandForestryUniversity,Lin′an311300,China2ZhejiangProvincialKeyLaboratoryofCarbonCyclinginForestEcosystemsandCarbonSequestration,Lin′an311300,China3AuthorityinNationalNatureReserveofTianmuMountain,Lin′an311300,China

Tree diameter structure is an important and basic role in forest structure. For the reason that the diameter at breast height (DBH) can be easily and accurately measured. Because it has a close relationship with variables such as stand density, tree age, tree height, canopy, biodiversity and so on, diameter structure is often used as a direct-response stand structure characteristic. DBH belongs to a set of non-spatial forest structure factors, and is frequently used to analyze the relationship between stand structure and growth, e.g. Recently, studies of forest spatial structure have expanded, partly due to the fact that the DBH is an important factor in explaining the growth of trees, and in many cases because the diameter structure has been used to analyze the relationship between spatial structure and DBH. Similarly, DBH is also an important factor in reflecting the growth of moso bamboo (Phyllpstachysedulis) forests. The DBH of moso bamboo can directly influence leaf area and root area volume, which affects the growth of moso bamboo. Others have performed a number of research studies on the relationship between DBH and other bamboo forest structure factors, such as bamboo height, age composition, canopy structure, and so on. However, these factors are generally measures of non-spatial structure. Recently, research suggests that a distance-dependent spatial index can accurately describe the moso bamboo stand structure, and therefore it is important to analyze and control the relationship between moso bamboo stand structure and function. Previous studies rarely reported the relationship between moso bamboo stand spatial structure and diameter. Therefore, three spatial structure parameters, uniform angle index, neighborhood comparison and age mingling degree were used to analyze the relationship between moso bamboo spatial structure and diameter, and thus provide a theoretical basis for sustainable moso bamboo forest management. The study was established in a close-to nature moso bamboo stand in Tianmu Mountain National Nature Reserve, Zhejiang province. The study design involved a fixed plot of 1hm2(100 m×100 m), which was divided into 100 units by adjacent grid inventory. Each moso bamboo was located in terms ofx-,y-, andz-coordinates using a Total Station. Three spatial structure parameters, including neighborhood comparison, uniform angle index, age mingling degree were evaluated. The DBH was recorded into one of three classes: Ⅰclass (DBH < 7 cm), Ⅱ class (7 cm ≤ DBH < 13 cm), Ⅲ class (DBH ≥ 13 cm). These classes were used to analyzed the relationship between spatial structure and DBH of the close-to-nature moso bamboo stand. The results showed that the frequency distribution of DBH had a right-skewed normal distribution, which is the similar to even-aged arbor stands. The spatial pattern of class Ⅱand class Ⅲ was of random distribution, similar to the distribution of the whole stand, but the pattern of class Ⅰshowed an aggregation distribution pattern. The uniform angle indexes decreased with increasing diameter classes, and results showed that the uniform index had a powerful relationship with DBH, with the determination coefficient between DBH and uniform index being 0.7793. The uniform angle of different diameter classes showed no obvious significant difference (P>0.05). The neighborhood comparison showed that for stands in an intermediate status, the DBH differentiation was not significant. The neighborhood comparison values showed that the ranking of the dominant degree was: Ⅲ>Ⅱ>Ⅰ. And the neighborhood comparisons decreased with increasing diameter classes, as well as had a significantly linear correlation with DBH (the determination coefficient was 0.9233). The neighborhood comparison of different diameter classes showed significant differences (P<0.01). The average age mingling of the stand was 0.8178, suggesting the age mingling intensity was intensive. The age mingling values showed the ranking of age segregation was: Ⅲ>Ⅱ>Ⅰ. And age mingling increased with increasing diameter classes, as well as had a strong relationship with DBH, where the determination coefficient was 0.6774. The age mingling of different diameter classes was also significanly different (P<0.01).

Phyllostachysedulisstand; spatial structure; diameter at breast height; uniform angle index; neighborhood comparison; age mingling degree

国家自然科学基金(31170595); 国家“十二五”科技支撑计划(2012BAD22B0503); 浙江省重点科技创新团队(2010R50030); 教育部留学回国人员科研启动金项目(20101561); 国家林业局造林司委托项目(SFA2130218- 2)

2013- 08- 25;

2014- 07- 02

10.5846/stxb201308252154

*通讯作者Corresponding author.E-mail: goodtmp@sohu.com

仇建习, 汤孟平, 沈利芬, 娄明华, 庞春梅.天目山近自然毛竹林空间结构与胸径的关系.生态学报,2015,35(12):4081- 4088.

Qiu J X,Tang M P, Shen L F,Lou M H, Pang C M.The relationship between spatial structure and DBH of close-to-naturePhyllostachysedulisstands in Tianmu Mountain.Acta Ecologica Sinica,2015,35(12):4081- 4088.