GM(1,1)正弦模型修补气温监测缺失数据的探讨
郭赞洪,唐其环
(西南技术工程研究所,重庆 400039)
环境条件对装备的使用或长期放置有重要的影响,文献[1—5]介绍了不同环境条件对于装备器械的影响,因此,了解环境的各性质很重要。其中,温度是气象站或者相关试验站所要监测的一个基本气象因素。由于在监测过程中,仪器的突然损坏、采集数据记录时突然出错等原因,会造成某段时间温度数据的缺失,如何对这部分数据进行修补至关重要。同时,环境温度受到各种自然环境因素的影响,温度变化难以预测,但是对于大部分天气没有突然转变的情况,温度变化是具有一定的规律性的。文中将对具有规律性的温度数据进行缺失修补研究分析。文静等人[6]研究了人工监测数据和自动站监测数据的相互填补,但随着信息自动化,人工检测将被完全取代。灰色系统法[7—9]中的GM(1,1)模型法近些年在许多领域中常用于缺失数据修补[7—9],而且是灰色系统法中应用最多的方法[10]。
GM(1,1)标准模型法适合于具有指数型性质增加或减小的数据[11—14],而不是所有的数据都恰好满足这样的要求。因此,不同领域的学者们对GM(1,1)标准模型进行改进,以适用于该领域数据变化情况[15—21]。Zou Lihua[22]、倪凯[23]和彭涛[24]分别在振动数据、量测数据和软基沉量数据方面采用将GM(1,1)模型进行研究改进,结果可知,针对不同数据变化规律将GM(1,1)模型进行改进后,预测效果得到了较大的提高。唐五湘等人[25—26]提出的时序修正法改进后的GM(1,1)模型即GM(1,1)时序修正模型,对于某些时序数据的预测具有一定的改进。文中研究的对象是大气温度数据,根据大气温度数据的变化情况,提出了以正弦函数对GM(1,1)标准模型进行改进,得到GM(1,1)正弦修正模型,对大气温度数据具有较好的预测修补作用。
文中将以万宁试验站监测的温度数据作为原始数据,采用GM(1,1)正弦修正模型与GM(1,1)时序修正模型以及GM(1,1)标准模型进行缺失修补对比分析研究。
1 数学模型
1.1 GM(1,1)标准模型
根据GM(1,1)标准模型法的建模过程要求,对原始数据X(0)数据进行一次累加生成得到X(1),如下:
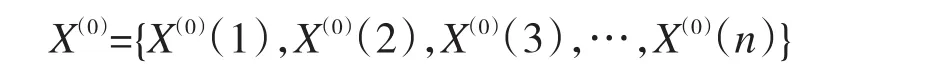
作一次累加公式为:

建立X(1)如下的白化微分方程为:

式(2)中的a和u为待求参数,记参数列为:

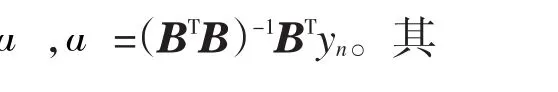
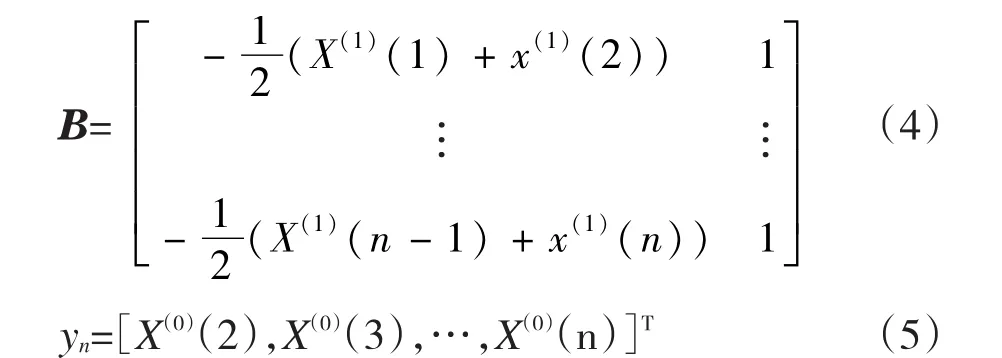
解出白化微分方程的解为:

式(4)即为通过原始数据建立起来的GM(1,1)模型。
1.2 GM(1,1)时序修正模型
根据唐五湘[25]提出的时序修正法对GM(1,1)模型进行改进。该文提出GM(1,1)标准模型已经确定了参数a和b,在模型中只剩下参数t,最终的预测精度就只和参数t相关,因而该作者讨论了输入变量t的GM(1,1)模型。该模型的建立过程如下:

将式(9)代入式(7)得到:

式(10)即为GM(1,1)时序修正模型。
1.3 GM(1,1)正弦修正模型
根据大气温度的类似周期变化性质,每天的温度变化类似于正弦函数的变化规律。文中提出了以正弦函数sin x修正GM(1,1)标准模型后的GM(1,1)正弦修正模型。并且将GM(1,1)模型中的t以24 h的整点时间带入,即t∈(1,2,…,24),经过试验带入,过程如下。
标准模型为:


经检验后,模型建模部分采用标准模型建模,预测部分采用改进5建模。因为标准模型和改进5模型分段使用时具有较好的拟合性,对该类温度数据具有较好的适应性。故GM(1,1)正弦修正模型为:

其中n为建模时的原始数据个数。
2 实例应用
文中以万宁试验站所监测的温度数据为基础,对以上模型进行检验。该试验站9月份的连续小时温度数据见表1。根据表1的原始数据建立相应模型。
2.1 GM(1,1)模型建立
用前9个数据作为原始数据建立GM(1,1)模型。

表1 万宁试验站9月份的某天的24 h温度数据Table 1 24 hour temperature data in Wanning test station on one day in September
2.2 GM(1,1)标准模型

根据表1、式(3)和式(4),建立GM(1,1)标准模型为:将⊗t带入式(9)和式(10)中,得到GM(1,1)时序修正模型,即为:

2.3 GM(1,1)时序修正模型
根据式(8)可以求出具体数值,见表2。
2.4 GM(1,1)正弦修正模型
根据原始数据和式(11),可以求出GM(1,1)正弦修正模型为:


表2 ⊗t的计算值Table 2 The calculated values of⊗t
3 结果分析
分别对式(12),(13)和(14)进行计算,对结果进行精度检验,得到绝对误差和相对误差精度检验。见表3。(预测精度=1-相对误差)
分析表3数据可知,从模型的拟合情况分析,GM(1,1)正弦修正模型与GM(1,1)标准模型具有相同的拟合平均误差(和平均相对误差),平均绝对误差只有0.2,平均相对误差也仅0.60%,具有与原始数据相当好的拟合效果。GM(1,1)时序修正模型的拟合平均绝对误差为0.6,平均相对误差为2.29%,虽然略大于另外两种,但拟合效果也不错。预测值的准确性的程度才是我们最关心的,GM(1,1)标准模型的预测平均绝对误差为6.7,平均相对误差为22.54%;GM(1,1)时序修正模型的预测平均绝对误差为5.3,平均相对误差为17.70%;GM(1,1)正弦修正模型的预测平均绝对误差为0.9,平均相对误差为3.14%。无论是从平均绝对误差还是相对误差来分析,GM(1,1)正弦修正模型相较于GM(1,1)标准模型和GM(1,1)时序修正模型有了很大的改进,预测的准确性得到了很大的提高。GM(1,1)标准模型的预测值的误差基本都超过了20%,GM(1,1)时序修正模型的预测误差也超过17%,而GM(1,1)正弦修正模型的预测误差绝大部分未超过6%,非常好地预测了原始值。
GM(1,1)标准模型、GM(1,1)时序修正模型、GM(1,1)正弦修正模型与原始数据的图形对比如图1所示,从模型的拟合分析来看,前9个点为模型拟合,GM(1,1)标准模型和GM(1,1)正弦修正模型的拟合很好,GM(1,1)时序修正模型的拟合相对较差一些。从预测部分看,GM(1,1)正弦修正模型从趋势和数值上很好地贴近原始数据的变化情况,而GM(1,1)标准模型和GM(1,1)时序修正模型则与原始数据相差太多,也未能符合原始数据的变化趋势,数值上也相差太多,所以,GM(1,1)正弦修正模型的预测效果远高于另外两种模型。因而,无论从模型拟合还是预测效果上,GM(1,1)正弦修正模型都比另外两种好很多,GM(1,1)正弦修正模型的预测值反应出了原始数据的变化规律,很好地预测了缺失数据。

图1 GM(1,1)标准模型、时序修正模型及正弦修正模型预测值与原始值比较Fig.1 Comparison of the predicted and original values of the GM(1,1)standard model,GM(1,1)timing corrected model and GM(1,1)sinusoidal model
总的来说,GM(1,1)标准模型的预测效果很差;GM(1,1)时序修正模型的预测效果虽然有一定的提高,但效果也不好;而GM(1,1)正弦修正模型预测效果高于前两种模型,很好地反映出了原始数据的变化规律,拟合很好。
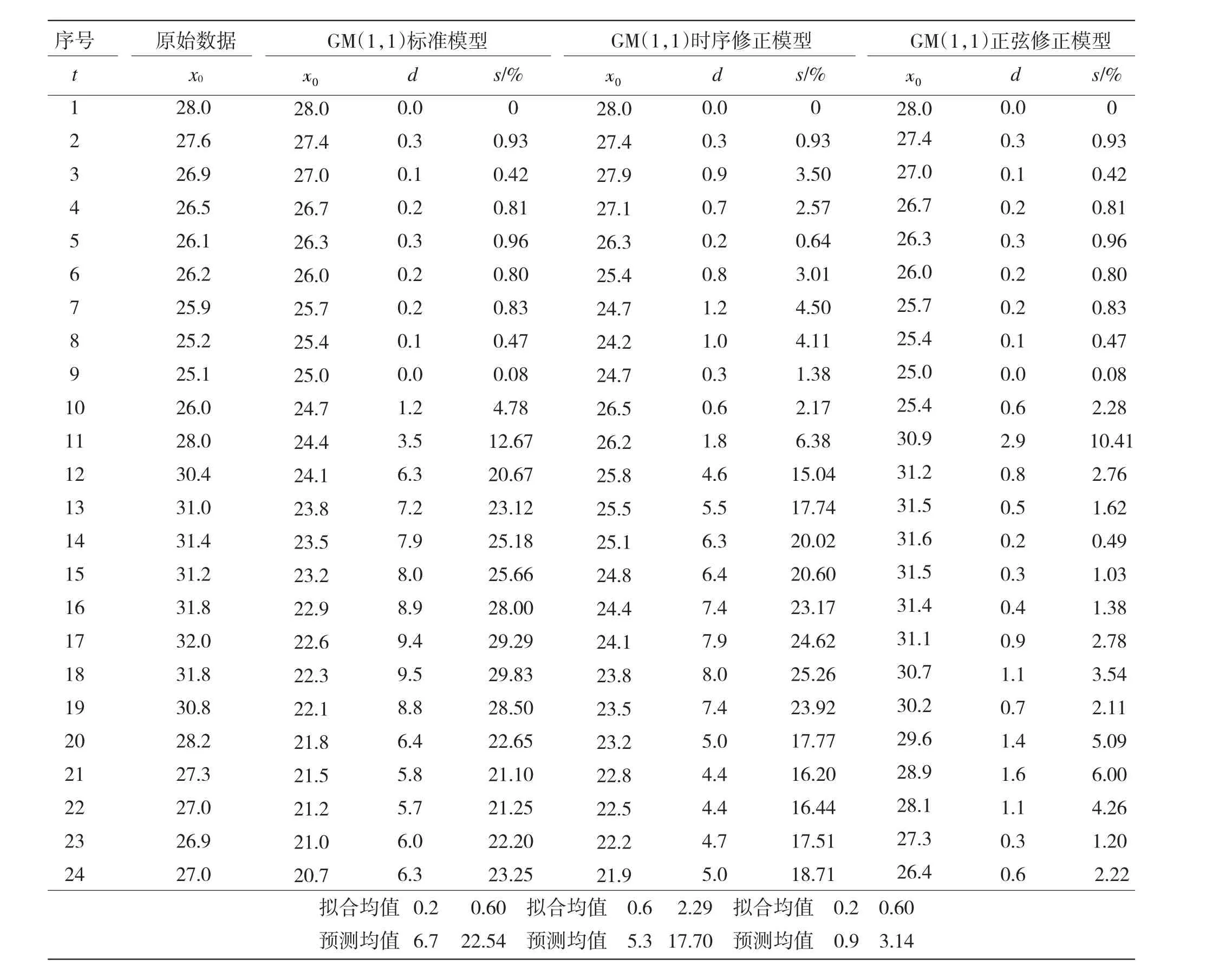
表3 三种模型的误差及其精度计算结果Table 3 The error and precision calculation results of the three kinds of models
4 结语
文中通过GM(1,1)正弦修正模型与GM(1,1)标准模型和GM(1,1)时序修正模型对环境温度数据进行建模预测,GM(1,1)正弦修正模型对比GM(1,1)标准模型和GM(1,1)时序修正模型有了很大的改进,且预测值很好地符合了原始数据的变化规律,预测精度较另外两种模型提高了很多,具有较高的预测精度。由于分析数据具有一定的局限性,该模型有待进一步研究。
[1] 陈川,王俊,黄海军,等.我国南沿海与欧洲沿海风电机组服役境条件的差异性分析[J].装备环境工程,2013,5(10):22—26.CHEN Chuan,WANG Jun,HUANG Hai-jun,et al.Discrepant Analysis between Service Conditions of Offshore Wind Turbine in Southeast China Coast and Europe Coast[J].Equipment Environmental Engineering,2013,5(10):22—26.
[2] 黄海军,李婵,王俊.典型大气腐蚀介质的灰色预测模型分析[J].装备环境工程,2012,1(9):13—16.HUANG Hai-Hun,LI Chan,WANG Ju.Study on Grey Prediction Model of Typical Atmospheric Corrosion Mediums[J].Equipment Environmental Engineering,2012,1(9):13—16.
[3] 陈群志,崔常京,王逾涯,等.典型机场地面腐蚀环境数据库研究[J].装备环境工程,2006,3(3):47—50.CHEN Qun-zhi,CUI Chang-ring,WANG Yu-ya,et al.Study on Database of Ground Corrosion Environment of Typical Airfield[J].Equipment Environmental Engineering,202006,3(3):47—50.
[4] 张彩先,汪东林,蒋晓彦,等.环境温度对直升机的影响及测试数据处理方法研究[J].装备环境工程,2006,4(3):45—49.ZHANG Cai-xian,WANG Dong-lin,JIANG Xiao-yan,et al.Study of the Influences ofEnvironmental Temperature on Helicopter and the Test Data Processing Method[J].Equipment Environmental Engineering,2006,4(3):45—49.
[5] 李慧,黄海军,王俊,等.湿热沿海地区环境条件对风电组的影响分析[J].装备环境工程,2013,5(10):17—22.LI Hui,HUANG Hai-jun,WANG Jun,et al.Influence of Environment Conditions on Wind Generating Set in Hot and Humid Coastal Areas[J].Equipment Environmental Engineering,2013,5(10):22—26.
[6] 文静,胡滨,马宏艳.自动气象站与人工温湿度计观测温湿度的对比研究[J].装备环境工程,2009,2(6):32—35.WEN Jing,HU Bin,MA Hong-yan.Comparative Study of Temperature and Humidity Observation with Automatic Weather Station and Manual Operation[J].Equipment Environmental Engineering,2009,2(6):32—35.
[7] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,2005.DENG Ju-long.The Basic Method of Grey System[M].Wuhan:Huazhong University of science and Technology Press,2005.
[8] 傅立.灰色系统理论及其应用[M].北京:科学技术文献出版社,2010.FU Li.Grey system theory and its application[M].Beijing:Science and Technology Literature Press,2010.
[9] 刘思峰.灰色系统理论的产生、发展及前言动态[J].浙江万里学院学报,2003,16(40):14—17.LIU Si-feng.Grey System Theory Generation,Development and Advanced Dynamic[J].Journal of Zhejiang Wanli University,2003,16(40):14—17.
[10]YIN Mu-shang.Fifteen Years of Grey System Theory Research:A Historical Review and Bibliometric Analysis[J].Expert Systems with Applications,2013(40):2767—2775.
[11]CHEN Chun,HUANG Shou-jen.The Necessary and Sufficient Condition for GM(1,1)Grey Prediction Model[J].Applied Mathematics and Conputation,2013,219:6152—6162.
[12]王正新,党耀国,赵洁钰.优化的GM(1,1)幂模型及其应用[J].系统工程理论与实践,2012,32(9):1973—1978.WANG Zheng-xin,DANG Yao-guo,ZHAO Jie-yu.GM(1,1)Power Optimization Model and Its Application[J].System Engineering Theory and Practice,2012,32(9):1973—1978.
[13]HSU Yen-tseng,LIU Ming-chung,JEROME Yeh,et al.Forecasting the turning Time of Stock Market Based on Markov-Fourier Grey Model[J].Expert Systems with Applications,2009(36):8597—8603.
[14]郑文琛,吉培荣,罗贤举.改进无偏GM(1,1)模型及其在长期电力负荷预测中的应用[J].继电器,2008,36(5):36—40.ZHENG Wen-chen,JI Pei-rong,LUO Xian-ju.Improvement of Unbiased GM(1,1)Forecasting Model in the Long Term Power Load and Its Application[J].Electric Relay,2008,36(5):36—40.
[15]LIN Yong-huang,LEE Pin-chan,CHANGTa-peng.Adaptive and High-precision Grey Forecasting Model[J].Expert Systems with Applications,2009(36):9658—9662.
[16]LIN Yong-huang,LEE Pin-chan.Novel High-precision Grey Forecasting Model[J].Automation in Construction,2007(16):771—777.
[17]XIE Nai-ming,LIN Si-feng.Discrete Forecasting Model and Its Optimization[J].Applied Mathematical Modelling,2009(33):1173—1186.
[18]CUI Jie,LIU Si-feng,ZENG Bo,XIE Nai-ming.A novel greyforecastingmodeland itsoptimization.Applied Mathematical Modeling,37(2013):4399—4406.
[19]JIN Xu,TAO Tan,MAO Tu,et al.Improvement of Grey Models by Least Squares[J].Expert Systems with Applications,2011(38):13961—13966.
[20]HSU Li-chang,WANG Chao-hung.Forecasting the Output of Integrated Circuit Industry Using a Grey Model Improved by the Bayesian Analysis[J].Technological Forecasting&Social Change.2007(74):843—853.
[21]李明洋,姜福川.基于最小二乘法的灰色GM(1,1)改进模型在非煤矿山事故预测中的作用[J].中国安全生产科学技术,2013,11(9):83—90.LI Ming-yang,JIANG Fu-chuan.The Improved GM(1,1)Model in the Prediction of Non Coal Mine Accidents Based
on Least Squares Function[J].Journal of Safety Science and Technology,2013,11(9):83—90.
[22]ZOU Li-hua,DAI Su-liang,JOHN B,et al.Greyfor Forecasting Model Active Vibration Control Systems[J].Journal of Sound and Vibration,2009,322:690—706.
[23]倪凯.灰色系统在量测数据处理中的应用[J].中国水运,2012,12(8):47—49.NI Kai.Grey System in Measure Ment Data Handl[J].Chinese Waterway,2012,12(8):47—49.
[24]彭涛,杨岸英,梁杏,等.BP-神经网络与灰色系统法的联合模型来预测软基沉降量[J].岩土力学,2005,26(11):1810—1814.PENG Tao,YANG An-ying,LIANG Xing,et al.The Joint Model of BP-neural Net Work and Grey System Method to Predict Soft Ground Settlement[J].Rock and Soil Mechanics,2005,26(11):1810—1814.
[25]唐五湘.GM(1,1)时序修正模型及其应用[J].云南环境科学,2003,22(4):20—21,45.TANG Wu-xiang.GM(1,1)Timing Correction Model and Its Application[J].Yunnan Environment Science,2003,22(4):20—21,45.
[26]李希灿,李丽.时序残差GM(1,1)模型[J].系统工程与理论,1998,18(10):59—63.LI Xi-chan,LI Li.Time Residuals GM(1,1)Model[J].System Engineering and Theory,1998,18(10):59—63.

