一种基于Q矩阵理论朴素的认知诊断方法*
(江西师范大学心理学院,南昌 330022)
1 引言
通常将对个体知识结构、加工技能或认知过程的诊断评估称之为认知诊断评估(Cognitive Diagnosis Assessment,CDA)或认知诊断(Cognitive Diagnosis,CD,Leighton &Gierl,2007)。与一般的教育考试不同,认知诊断使用融合了相关认知变量的心理计量学模型对被试进行诊断评估。这使得测验不再局限于单一而笼统的分数,而是能够提供关于被试认知水平更加详细的诊断信息,从而更深入地了解学生的认知结构与水平。据统计,认知诊断方法发展至今已达100多种(辛涛,乐美玲,张佳慧,2012)。其中,受研究者关注较多的有:(Tatsuoka,1991,1995;Tatsuoka &Tatsuoka,1997)的规则空间方法(Rule Space Method,RSM),Junker和Sijtsma(2001)的决定性输入,噪音‘与’门模型(the Deterministic Inputs,Noisy “and” Gate Model,DINA),Leighton,Gierl和 Hunka(2004)以及 Leighton和Gierl(2007)的属性层次方法(Attribute Hierarchy Method,AHM),等等。
Q矩阵理论和认知诊断方法是认知诊断的两个重要组成部分。作为认知诊断的基础,Q矩阵理论包含以下几个核心概念:Q矩阵、邻接矩阵(Adjacency Matrix,简称为 A 矩阵)、可达矩阵(Reachability Matrix,简称为R矩阵)、理想掌握模式(Ideal Master Pattern,IMP)或知识状态(Knowledge States,KS)、典型项目考核模式及理想反应模式(Ideal Response Pattern,IRP)。Q矩阵是描述测验项目与属性间关系的关联矩阵。A矩阵是反映属性间直接关系的矩阵。R矩阵是反映属性间直接关系、间接关系和自身关系的矩阵。IMP是根据属性间的层级关系确定的所有符合逻辑的掌握模式,也称之为KS。典型项目考核模式是根据属性间层级关系确定的所有符合逻辑的测验项目考核模式。IRP是被试在不存在任何失误和猜测误差条件下对项目的作答反应。
在界定好上述矩阵后,便可利用相应的认知诊断方法对被试进行诊断评估。以 RSM 为例,其基本思想是利用被试的观察反应模式(Observed Response Pattern,ORP)来推断其潜在的不可直接观察的属性掌握模式(Attribute Master Pattern,AMP)。大致步骤是:基于Q矩阵理论,建立起IMP与IRP之间的一一对应关系,再利用其构建的二维规则空间,采用 Bayes判别法对被试进行事后诊断分类。而AHM在RSM的基础上,认为应当先获得Q矩阵再编制测验。其判别分类方法主要包括两种:A方法和B方法。A方法将需判别的ORP与所有的IRP逐个比较,求取二者的相似的概率,按概率最大的准则进行诊断分类。B方法将ORP与所有的IRP进行逐个比较,确定不包含在该ORP中的IRP,计算其1-0型失误的概率,按概率最大的准则进行诊断分类。
受AHM启发,结合丁树良等人(2009,2010)提出的改进的Q矩阵理论,孙佳楠等人(2011)提出了广义距离判别法(Generalized Distance Discrimination,GDD)。GDD引入项目反应理论(Item Response Theory,IRT)中的项目正确作答概率P
和(1-P)以及0,用以定义被试的ORP与IRP对应位置元素间的广义距离,再计算被试的ORP与每种IRP之间的广义距离,按距离最短准则直接对被试的 ORP进行分类。GDD以 DINA模型为基准,与 RSM 和AHM的A方法在相同实验条件下相比,具有更好的分类效果。需要注意的是,现存的认知诊断方法通常依托于特定的心理计量学模型。因此,如何获得精确的模型参数是整个方法的关键。这其中的数学运算量大且复杂。虽然已有少量专业软件可供使用,但基本上都要求使用者有较扎实的测量学基础。在某些情境下甚至需要进行计算机编程才能实现参数估计。换言之,使用者的学习“成本”较高。但是,在实际情境中,认知诊断测验的使用者多为中小学的一线教师。若要求他们花费较多时间在理解如何使用某种认知诊断方法上,势必会影响日常的教学工作。这显然是不合理的,也与研究者开发认知诊断方法进行辅助教学的初衷相违背。因此,认知诊断方法的简单化具有重要的实践意义。
本研究提出一种直接利用被试的作答信息对被试进行诊断分类的方法,即海明距离判别法(Hamming Distance Discrimination,HDD)。使用海明距离(Hamming Distance,HD)定义被试的ORP与每种IRP之间的距离,根据距离最短准则对被试进行诊断分类。按照判别方式的不同,将HDD分为B方法和R方法。通过Monte Carlo模拟研究,探查HDD的 B方法和 R方法的诊断分类效果,并与GDD进行比较。
2 规则空间方法、广义距离判别法概述
2.1 规则空间方法(RSM)
RSM分为两大部分,Q矩阵的确定和规则空间的构建及判别,基本步骤如下:
(1)建立项目与属性间的关系,构造Q矩阵,计算所有可能的IMP及对应的IRP;
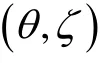
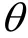
2.2 广义距离判别法(GDD)
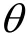
3 海明距离判别法(Hamming Distance Discrimination,HDD)
3.1 海明距离(HD)
海明距离,有时译成汉明距离。在信息论中,海明距离指两个等长字符串对应位置的不同字符的个数。如,字符串A(1,0,1)与字符串B(0,1,0)的对应位置的不同字符个数为3,即A与B的海明距离为3。海明距离被用于海明码(Hamming Code)中,对编码进行检错和纠错(Hamming,1950)。
3.2 定义反应模式间的海明距离(Hamming Distance between Response Patterns,HDRP)
不考虑测验中被试的ORP缺失的情况,在0-1计分项目的认知诊断测验中,我们将被试i
的 ORP与第t
种IRP之间的海明距离定义为: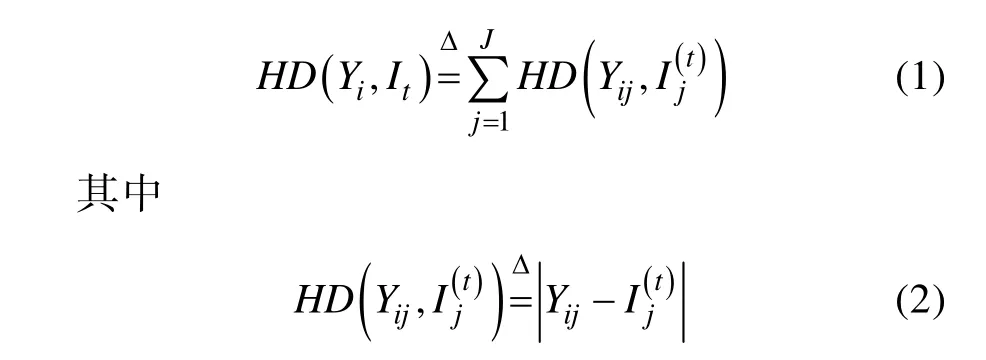
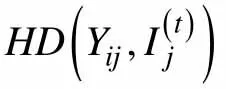
3.3 海明距离判别法(HDD)的合理性
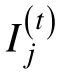
第二,判别方法的合理性。由于 ORP与 IRP对应位置的元素间的海明距离均为非0即1的整数,使得必然会出现某个被试的ORP与多个IRP间的海明距离相同且均为最小值的情况(本研究中各种实验条件下符合该情况的被试占总人数的比例详见表1)。此时无法按照距离最短准则对被试进行判别。因此,必须采取某种判别方式对符合此种情况的被试此进行处理。根据判别方式的不同,本方法可分为R方法和B方法两种。R方法是从多个最小值对应的IRP中随机(Random)选取一种,再将其对应的 IMP作为被试的 AMP判别值。由于这些“特殊的”IRP是在剔除了大部分与被试的ORP相似度低的IRP后挑选出来的,在没有其它任何可辅助判别的信息的情况下,有理由认为该被试的 AMP恰好是这些“特殊的”IRP中任意一种所对应的IMP的概率均等。故使用随机选取的方式对其进行处理,是合理的。B方法参考RSM,对多个最小值的情况使用Bayes判别法,合理地利用了当前测验情境所提供的信息来辅助对被试的判别分类,能够减少误判,提高诊断结果的分类准确率。
3.4 应用海明距离法(HDD)作判别
HDD分为两大步:
第一步,计算被试i
的ORP与每种IRP之间的海明距离,并按距离最短原则对被试进行判别分类;第二步,运用R方法或B方法。
经过第一步,即可将被试分为两类,第一类被试能够找到与其ORP的海明距离最小的IRP,且该IRP是唯一确定的;第二类被试虽然也能找到与其ORP海明距离最小的IRP,但找出的IRP并不是唯一的。其中,第一类被试通过第一步即可完成诊断分类,而第二类被试需要继续进行第二步,即采用R方法或B方法中的一种,以实现分类的目标。R方法简单易懂,不再赘述。下面重点介绍如何使用B方法。
不难发现,第一类被试的判别分类结果实质上提供了关于此次测验情境的中各种IRP的分布信息,能够较好地体现当前被试群体的能力分布特点,有助于对第二类被试的分类判别。例如,当被试i
的ORP同时与IRP
和IRP
的海明距离最小时,若第一类被试中IRP
的判别人数更多,则有理由认为被试i
的AMP是IRP
所对应的IMP的概率更大。故利用第一类被试的判别结果计算IRP
的后验概率,方法如下:
N
为当前被试的总人数,n
为在这N
个被试中AMP为第t
种IRP对应的IMP的被试人数。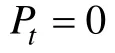
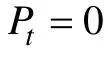
4 模拟研究
4.1 Q矩阵的设计
本研究采用与孙佳楠等人(2011)相同的实验条件,考察 Leighton等人(2004)给出的四种属性层级关系——直线型(Linear)、收敛型(Convergent)、发散型(Divergent)和无结构型(Unstructured)。除此之外,Tatsuoka(1995,2009)在其研究中还使用了属性间互不相关(unrelated)的一种属性层级关系。为表述方便,称之为独立型(Independent)。本研究将其纳入考察范围。至此,一共考察五种基本的属性层级关系(见附录 1)。根据属性间的层级关系,可以导出每种层级关系下的典型项目考核模式,它们分别为6个项目、7个项目、15个项目、32个项目和63个项目。为了尽量保证不同属性层级关系下的测验项目数基本一致,我们让五种典型项目考核模式分别在测验中重复出现5次、5次、2次、1次和1次。其中,独立型的属性层级关系下,由于题数的限制,只取了 63个项目中按项目考察属性的个数由小到大排序后的前30个项目。据此,五种属性层级关系的测验长度分别 30题、35题、30题、32题和30题(见附录2)。
4.2 被试作答反应矩阵的模拟
本研究中各种实验条件下的被试样本容量均为 1000人。根据属性层级关系可以求出五种属性层级关系下被试的IMP种类,分别为7种、8种、16种、33种和64种。结合4.1部分的Q矩阵设计,计算各种IMP对应的IRP,求取每种IRP对应的测验总分。按照标准正态分布确定各测验总分的人数分布,并使得测验总分相同的 IMP的被试人数一致。这样就得到了五种属性层级关系下服从标准正态分布的1000个被试的IMP。
根据五种属性层级关系下的 1000个被试的IMP及4.1 部分的Q矩阵设计,在没有任何失误和猜测的情况下,模拟被试在各测验项目上的 IRP。然后在IRP的基础上,采用Leighton 等人(2004)的模拟方法,模拟作答反应失误概率(slip)分别为2%,5%,10%和15%的情况下被试的作答反应矩阵。
4.3 模拟次数
每种实验条件下的模拟次数为50次。
4.4 模拟研究使用的判别分类法
对每种实验条件下模拟所得的被试作答反应矩阵,均采用HDD的B方法、R方法和GDD对其进行判别分类。
4.5 评价标准
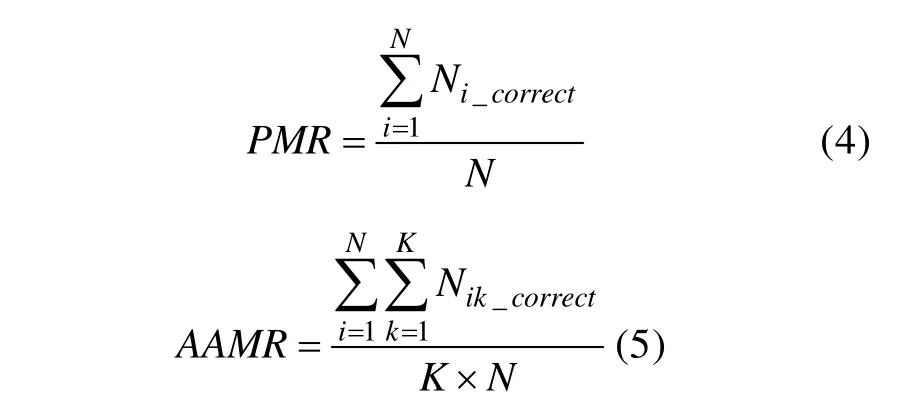
采用模式判准率(Pattern Match Ratio,PMR)和属性平均判准率(Average Attribute Match Ratio,AAMR)作为评价指标。二者公式如下:
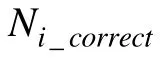
5 研究结果
ORP与多个 IRP的海明距离相同且均为最小值的被试占总人数的比例见表1。HDD中的B方法、R方法和 GDD的模式判准率(PMR)和属性平均判准率(AAMR)见表2及图1和图2。所有结果均为50次模拟的平均值。
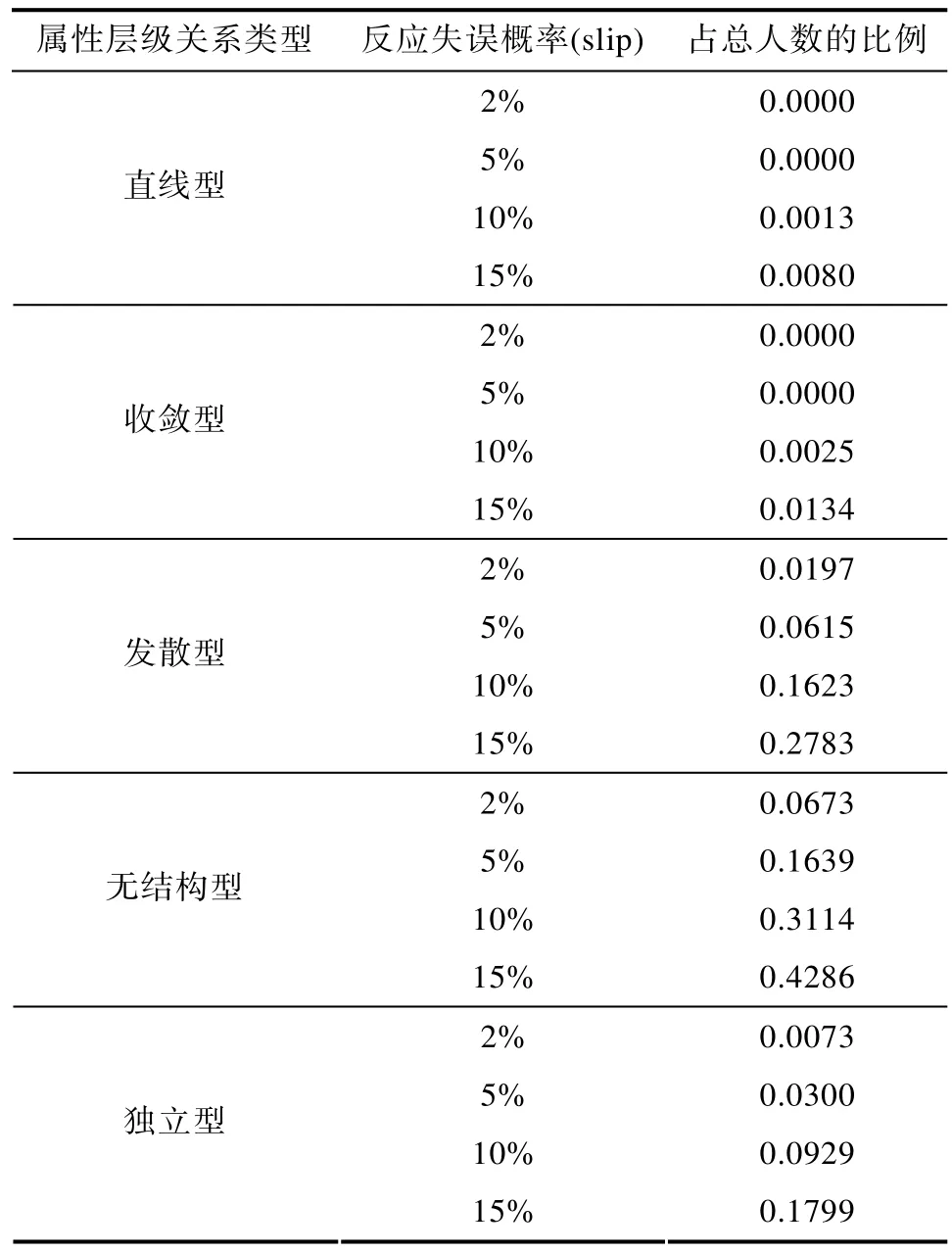
表1 ORP与多个IRP的海明距离相同且均为最小值的被试占总人数的比例
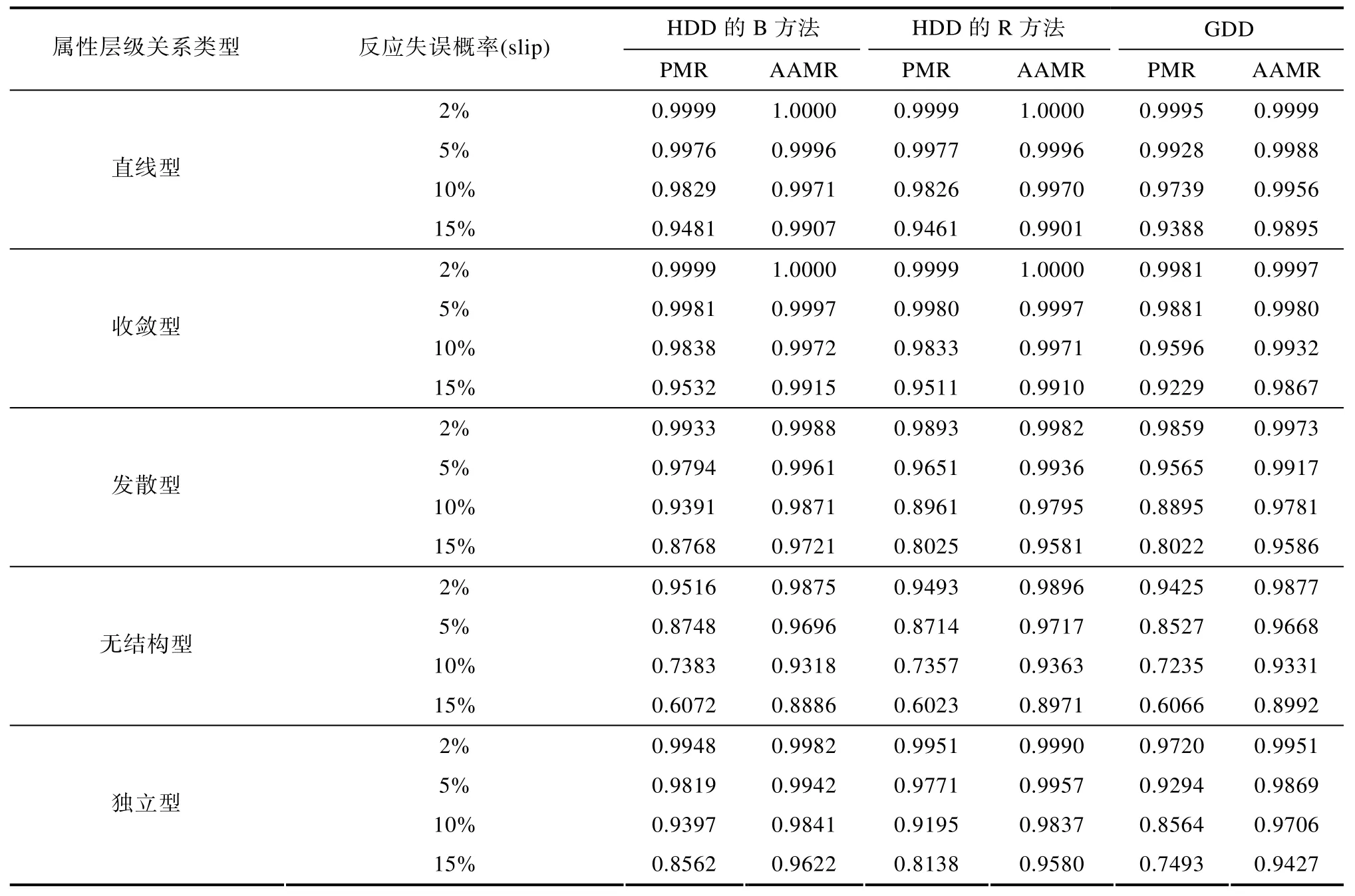
表2 HDD的B方法、R方法和GDD的模式判准率(PMR)和属性平均判准率(AAMR)
本研究的 Monte Carlo模拟实验中计算出的GDD的分类准确率,与已有文献的研究结果处于同一水平(孙佳楠等,2011;涂冬波等,2013;蔡艳等,2013)。
由表1可知,在五种属性层级关系下,ORP与多个IRP的海明距离相等且最小的被试占总人数的比例由低到高分别为直线型、收敛型、独立型、发散型、无结构型。
由表2可知,在五种属性层级关系下,分类准确率由高到低依次为HDD的B方法,HDD的R方法,GDD。其中,对直线型和无结构型的属性层级关系,HDD的B方法和R方法的PMR和AAMR均略高于GDD;对于收敛型、发散型和独立型的属性层级关系,HDD的B方法和R方法的PMR和AAMR均优于GDD。就HDD而言,在五种属性层级关系下,B方法的PMR和AAMR均高于R方法。其中,对于直线型、收敛型和无结构型的属性层级关系,B方法的PMR和AAMR略高于R方法;对于发散型和独立型的属性层级关系,B方法的PMR和AAMR要优于R方法。
由图1和图2可知,对同一种属性层级关系而言,随着作答反应失误概率(slip)的增加,HDD的B方法、R方法和GDD的PMR和AAMR均不断下降。其中,HDD的B方法的判别效果下降速度最慢,R方法次之,GDD下降较快。五种属性层级关系下,HDD的B方法和R方法与GDD的判别效果之间的差距均呈增加趋势。其中,对于直线型和无结构型的属性层级关系,三者的判别效果差距较小。对于收敛型、发散型和独立型的属性层级关系,三者的判别效果差距较大。
6 小结与讨论
6.1 研究结论
通过上述实验结果,可以得出以下结论:
(1)三种认知诊断方法的分类准确率均受属性层级结构的紧密程度的影响,属性层级关系越紧密,分类准确率越高。
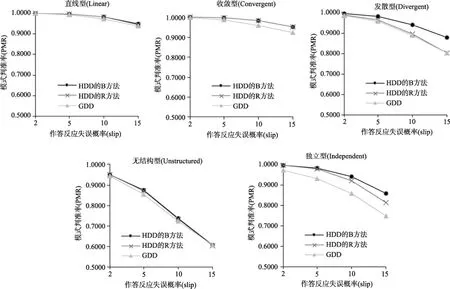
图1 HDD的B方法、R方法和GDD的知识状态的模式判准率比较
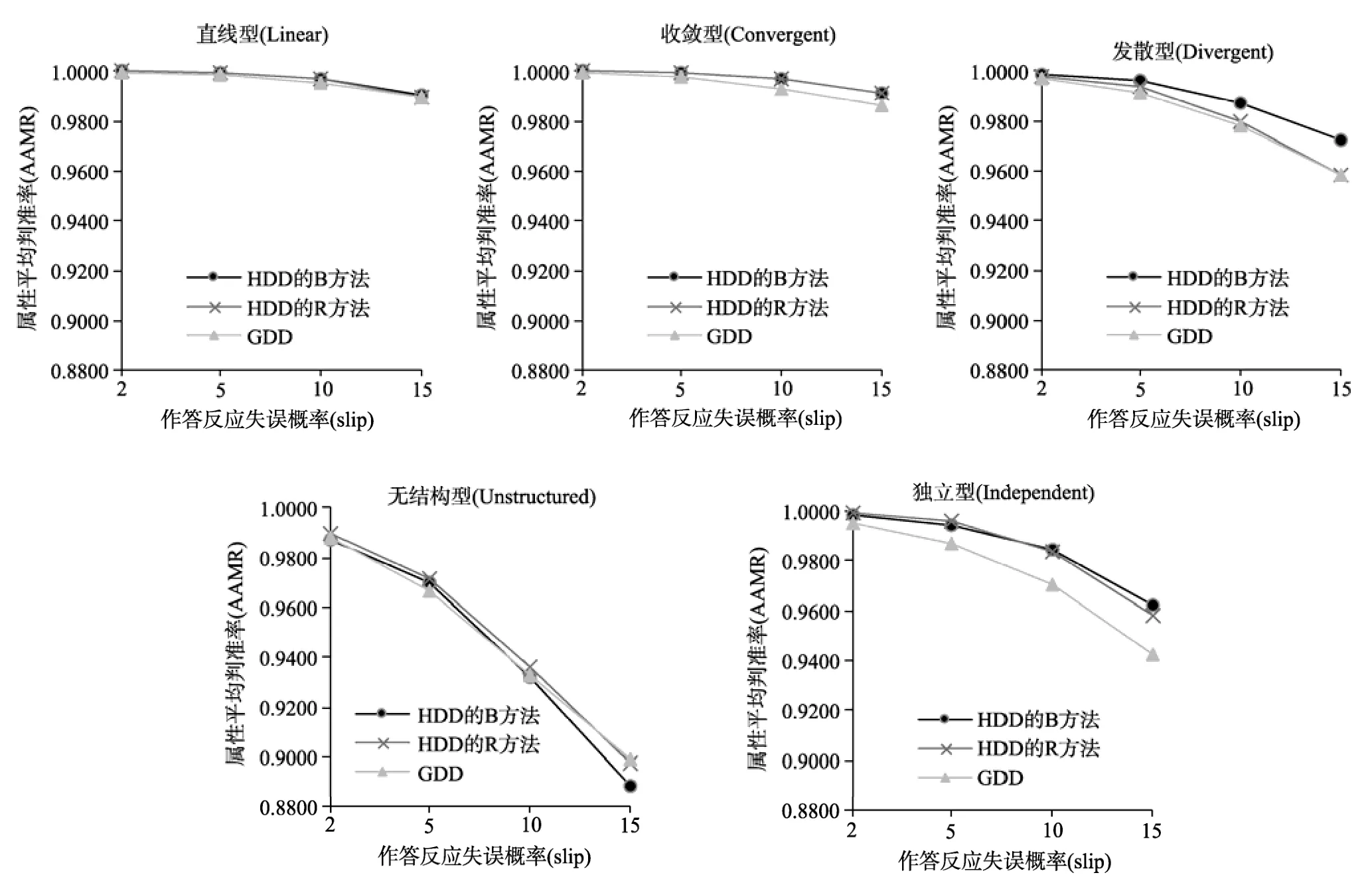
图2 HDD的B方法、R方法和GDD的知识状态的属性平均判准率比较
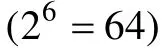
(2)总体而言,分类准确率由高至低分别为HDD的B方法,HDD的R方法,GDD。
GDD的本质是利用IRT模型中的2PLM项目特征函数对ORP与IRP之间的海明距离进行加权处理,再根据距离最小原则进行判别分类。在这个过程中,参数估计的误差在一定程度上影响了GDD的分类准确率。当被试的作答中包含有更大的误差因素(即实验中的 slip更大)时,参数估计的结果会更加不准确,因而对 GDD的分类准确率的影响也会更大。HDD则规避了这一误差来源,且方法本身所依据的逻辑合理,因此HDD的B方法和R方法都具有较高的分类准确率。
6.2 HDD的特点分析
DiBello和Stout(2007)认为,模型的参数应当足够复杂,以便提供尽可能多的诊断信息,但是,在模型的参数拟合数据的情况下也应该足够简单,以满足实践者的需要。因此,当两种认知诊断方法具有同等水平的分类准确率时,操作更加简单的认知诊断方法显然更佳。DINA模型和 GDD就是其中的代表。与现有认知诊断方法相比,本研究所提出的 HDD在具有较高的分类准确率的同时,并没有引入额外的参数,具有零参数的特点,不需要进行参数估计。因此,可以避免因估计方法的误差而导致分类准确率下降的不良后果。与此同时,不需要参数估计的特点使HDD的操作步骤非常简单。理论上,只要获取被试的作答数据,进行简单的加减运算即可对被试进行诊断分类,故称之为“朴素的”认知诊断方法。运用HDD可以大大降低中小学一线教师实施认知诊断测验的难度,有助于认知诊断测验的推广和应用。但零参数的特点有利也有弊,弊在于HDD无法同其他认知诊断方法一样获得项目参数,也就无法实现对项目性能的量化描述。因此,在 1-0计分的认知诊断测验中,当需要获取项目参数时,可考虑使用其他认知诊断方法。
6.3 B方法与R方法
HDD的B方法的分类准确率相对于R方法而言更高,但Bayes判别对于样本容量较为敏感。当后验概率不准确时,B方法的分类准确率必然会受到影响。R方法便适用于此种情况。故建议在实施认知诊断测验时,被试量较小时,可以使用 R方法。被试量较大时,则改用B方法,可以得到更好的分类效果。
7 展望
本研究在Monte Carlo模拟研究的情境下,对HDD在 0-1评分的认知诊断测验中的分类效果进行了探讨。然而,实际情境中被试的作答可能会受到多种因素的影响。因此,需要使用实测数据从多方面对 HDD进行效度验证。此外,还可以开发适用于多级评分及混合评分的HDD,使得HDD能够应用于不同的测验情境。
Cai,Y.,Tu,D.B.,&Ding,S.L.(2013).A simulation study to compare five cognitive diagnostic models.Acta Psychologica Sinica,45
(11),1295–1304.[蔡艳,涂冬波,丁树良.(2013).五大认知诊断模型的诊断正确率比较及其影响因素:基于分布形态、属性数及样本容量的比较.心理学报,45
(11),1295–1304.]DiBello,L.V.,&Stout,W.(2007).Guest editors’ introduction and overview:IRT-based cognitive diagnostic models and related method.Journal of Educational Measurement,44
(4),285–291.Ding,S.L.,Yang,S.Q.,&Wang,W.Y.(2010).The importance of reachability matrix in constructing cognitively diagnostic testing.Journal of Jiangxi Normal University(Natural Science),34
(5),490–494.[丁树良,杨淑群,汪文义.(2010).可达矩阵在认知诊断测验编制中的重要作用.江西师范大学学报(自然科学版),34
(5),490–494.]Ding,S.L.,Zhu,Y.F.,Lin,H.J.,&Cai,Y.(2009).Modification of Tatsuoka’s Q matrix theory.Acta Psychologica Sinica,41
(2),175–181.[丁树良,祝玉芳,林海菁,蔡艳.(2009).TatsuokaQ矩阵理论的修正.心理学报,41
(2),175–181.]Junker,B.M.,&Sijtsma,K.(2001).Cognitive assessment models with few assumptions,and connections with nonparametric item response theory.Applied Psychological Measurement,25
(3),258–272.Leighton,J.P.,&Gierl,M.(2007).Cognitive diagnostic assessment for education:Theory and Applications
(pp.242–274).Cambridge,UK:Cambridge University Press.Leighton,J.P.,Gierl,M.J.,&Hunka,S.M.(2004).The attribute hierarchy method for cognitive assessment:A variation on Tatsuoka's rule-space approach.Journal of Educational Measurement,41
(3),205–237.Hamming,R.W.(1950).Error detecting and error correcting codes.The Bell System Technical Journal,29
(2),147–160.Sun,J.N.,Zhang,S.M.,Xin,T.,&Bao,Y.(2011).A cognitive diagnosis method based on Q-Matrix and generalized distance.Acta Psychologica Sinica,43
(9),1095–1102.[孙佳楠,张淑梅,辛涛,包钰.(2011).基于 Q 矩阵和广义距离的认知诊断方法.心理学报,43
(9),1095–1102.]Tatsuoka,K.K.(1991).Boolean algebra applied to determination of universal set of knowledge states
(Tech.Rep.RR–91–44–ONR).Princeton,NJ:Education Testing Service.Tatsuoka,K.K.(1995).Architecture of knowledge structure and cognitive diagnosis:A statistical pattern recognition and classification approach.In P.D.Nichols,S.F.Chipman,&R.L.Brennan(Eds.),Cognitively diagnostic assessment
(pp.327–361).Hillsdale,NJ:Erlbaum.Tatsuoka,K.K.,&Tatsuoka,M.M.(1997).Computerized cognitive diagnostic adaptive testing:Effect on remedial instruction as empirical validation.Journal of Educational Measurement,34
(1),3–20.Tatsuoka,K.K.(2009).Cognitive assessment:An introduction to the rule space method.
Routledge,New york,NY 10016.Tu,D.B.,Cai,Y.,&Dai,H.Q.(2013).Comparison and selection of five noncompensatory cognitive diagnosis models based on attribute hierarchy structure.Acta Psychologica Sinica,45
(2),243–252.[涂冬波,蔡艳,戴海琦.(2013).几种常用非补偿型认知诊断模型的比较与选用:基于属性层级关系的考量.心理学报,45
(2),243–252.]Xin,T.,Le,M.L.,&Zhang,J.H.(2012).New progress and trends of measurement theory.China Examinations,
(5),3–11.[辛涛,乐美玲,张佳慧.(2012).教育测量理论新进展及发展趋势.中国考试,
(5),3–11.]附录1 五种基本的属性层级关系
A.直线型(Linear)

B.收敛型(Convergent)
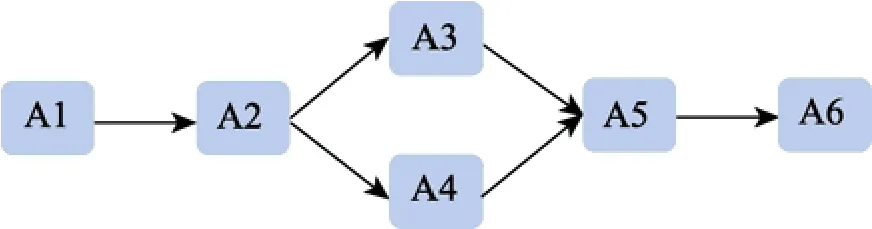
C.发散型(Divergent)
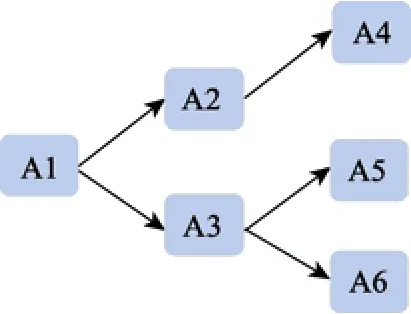
D.无结构型(Unstructured)
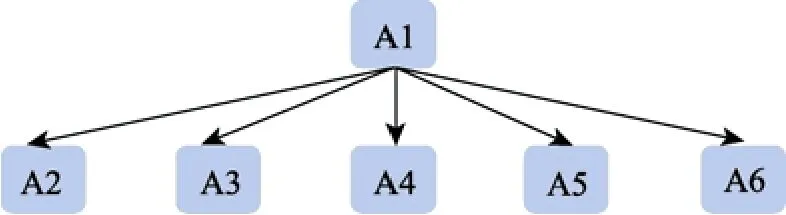
E.独立型(Independent)

附录2 五种基本的属性层级关系的Q矩阵
A.直线型(Linear)

B.收敛型(Convergent)

C.发散型(Divergent)

D.无结构型(Unstructured)

E.独立型(Independent)

附录3 直线型属性层级关系和独立型属性层级关系下的IRP
A.直线型(Linear)

B.独立型(Independent)
由于独立型属性层级关系下的IRP种类过多,仅列出其中15种:


