尘埃等离子体混合模型中电荷-电势问题的迭代法求解

马征征 徐 彬 许正文

(中国电波传播研究所 电波环境特性及模化技术重点实验室,山东 青岛 266107)

引 言

在电离层、等离子体和电波传播等领域的工程实际问题中,往往都需要求解电势场分布. 对于静电场,在电荷分布已知的条件下,通常由泊松方程来求解电势. 由于泊松方程是偏微分方程,难以获得解析解,因此，通常都使用数值计算方法. 常用的方法有解矩阵法、谱方法和迭代法等[1].

然而,许多空间等离子体环境中有可能出现尘埃粒子. 这些尘埃将不可避免地与背景等离子体相互作用:一方面,浸没在等离子体中的尘埃粒子将通过碰撞和电离等方式充放电荷,成为带电尘埃粒子;另一方面,带电尘埃将显著影响到等离子体中的动力学、电学、波动和不稳定等过程. 最终两者相互作用,形成所谓尘埃等离子体. 常见的尘埃等离子体现象有地球极区夏季冰晶云、行星际空间、彗星、行星环以及火箭喷焰等[2-4].

带电尘埃粒子的出现会使电势场求解变得复杂. 首先,对于总电荷分布,除了电子和离子还需增加考虑尘埃粒子. 由于尘埃携带电荷量可以很大且本身具有很大的惯性,容易形成非常不均匀的电荷空间分布. 另由于尘埃粒子相比电子具有大得多的质荷比,在模拟和求解某些问题时,需要对两者采用不同的处理方式,建立所谓混合模型. 常见的一类处理方式是:对尘埃粒子和离子采用动力学模拟,如质点网格(Particle-in-Cell,PIC)法,通过运动方程计算其分布;而对电子采用流模拟,如直接采用波尔兹曼分布[5-6]. 很重要地,此时电子电荷分布按照波尔兹曼分布律由电势决定;而电势通过泊松方程又由总电荷分布决定. 该问题不是直接由电荷求解电势的过程,我们将其称为“电荷-电势”问题. 可以想到,对于此问题,解矩阵法和谱方法的适用性降低.

在如分子生物物理学等其他领域中,也存在着类似的问题,并且已开展了不少针对该问题中泊松-波尔兹曼方程求解方法的研究[7]. 而在尘埃等离子体领域,针对此问题的研究较少. 本文针对尘埃等离子体领域的工程实际,考察迭代法的求解适用性.

1 求解原理

首先给出求解静电场中电势的泊松方程为

(1)

式中:ρ是电荷密度; 下标d、i、e分别代表尘埃粒子、离子和电子;ε0是真空中的介电常数.

混合模型中,尘埃粒子电荷密度ρd和离子电荷密度ρi由动力学模型计算得到. 由于本文不研究动力学模型,因此直接作为已知量给出. 电子电荷密度ρe满足波尔兹曼分布,有

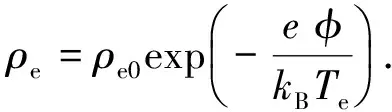
(2)

式中:e是电子电量;kB是波尔兹曼常数;Te是电子温度;ρe0是背景电子电荷密度.

最终由式(1)和(2)得到方程

f(φ) =2φ

=0.

(3)

注意到式(3)是偏微分的超越方程,解矩阵法和谱方法的适用性较低,因此考虑迭代法. 牛顿迭代法是平方收敛的,具有收敛速度快的特点. 其公式为

(4)

n表示迭代次数.

式(3)中还可以增加所谓下山因子ω,也称为牛顿下山法. 格式为

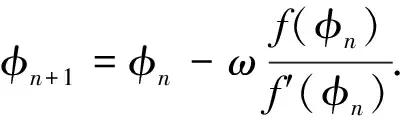
(5)

若采用固定值A0替代f′(φn),则

(6)

则被称为平行弦法,A0有时可取为f′(φ0). 下标0表示初始猜测值. 平行弦法的收敛速度通常相当于或低于牛顿迭代法,但省去了对函数导数的计算,节约了计算时间,且能够比牛顿迭代法更加稳定. 其中,下山因子的确定有理论依据,通常以满足|f(φn+1)|<|f(φn)|为原则. 但考虑到工程实际问题的复杂性,往往直接采用尝试取值的方法. 此外下山因子还可随迭代过程变化而取值[8].

2 求解过程及结果

2.1 牛顿下山法求解的简单例

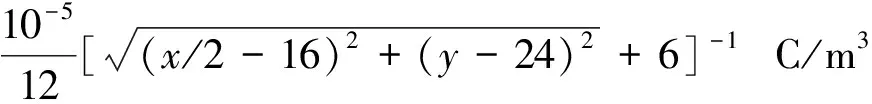
给出,且最小值为4.8×10-8C/m3. 其中x和y分别是网格横向和纵向编号. 如图1所示.

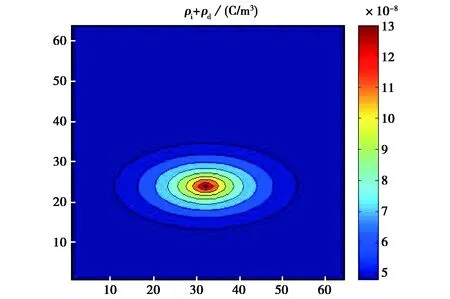
图1 尘埃粒子和离子总电荷密度二维分布简单例

电势的初始值按均匀分布给出,通过式(5)来迭代求解. 迭代过程中期望f(φ)的值逐渐趋近于0,f(φ)=0对应的电势值即为方程的解. 虽然实际求解过程中f(φ)=0往往难以实现,但f(φ)的值越接近0,对应的解也就越精确. 可用函数f(φ)的值来表征解的精度. 注意到f(φ)实际上是一个矩阵,可以通过定义式

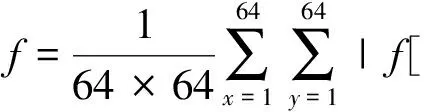
(7)

来表征迭代过程中解的精度. 对于下山因子,考虑了四种不同值. 最终得到了迭代过程中f值(对数)的变化,如图2所示.

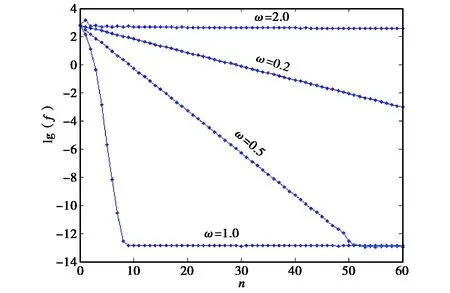
图2 不同下山因子下牛顿下山法求解简单例的收敛过程

可以看到当下山因子ω=0.2、0.5和1.0时,迭代过程均收敛. 同时,收敛速度随ω增大而加快. 当ω=1.0时,收敛速度非常快(9步). 此外,收敛后最终的f值约为10-13,表示解的精度非常高. 而当ω增大到2.0时,迭代不具收敛性. 这里我们取ω=1.0,得到迭代次数n=50时的电势解如图3所示,再由式(2)得到电子电荷密度解,如图4所示.

2.2 平行弦法求解工程实际中的复杂例

考察来自工程实际中尘埃等离子体离子声波不稳定性过程模拟的一个例子.网格为64×64,边长为0.005 m,采用周期边界条件[6]. 离子和带电尘埃粒子的分布为已知量,已由动力学模型计算得到,如图5所示. 可以看到,在带电尘埃粒子加入时,电荷的空间分布可以十分复杂.

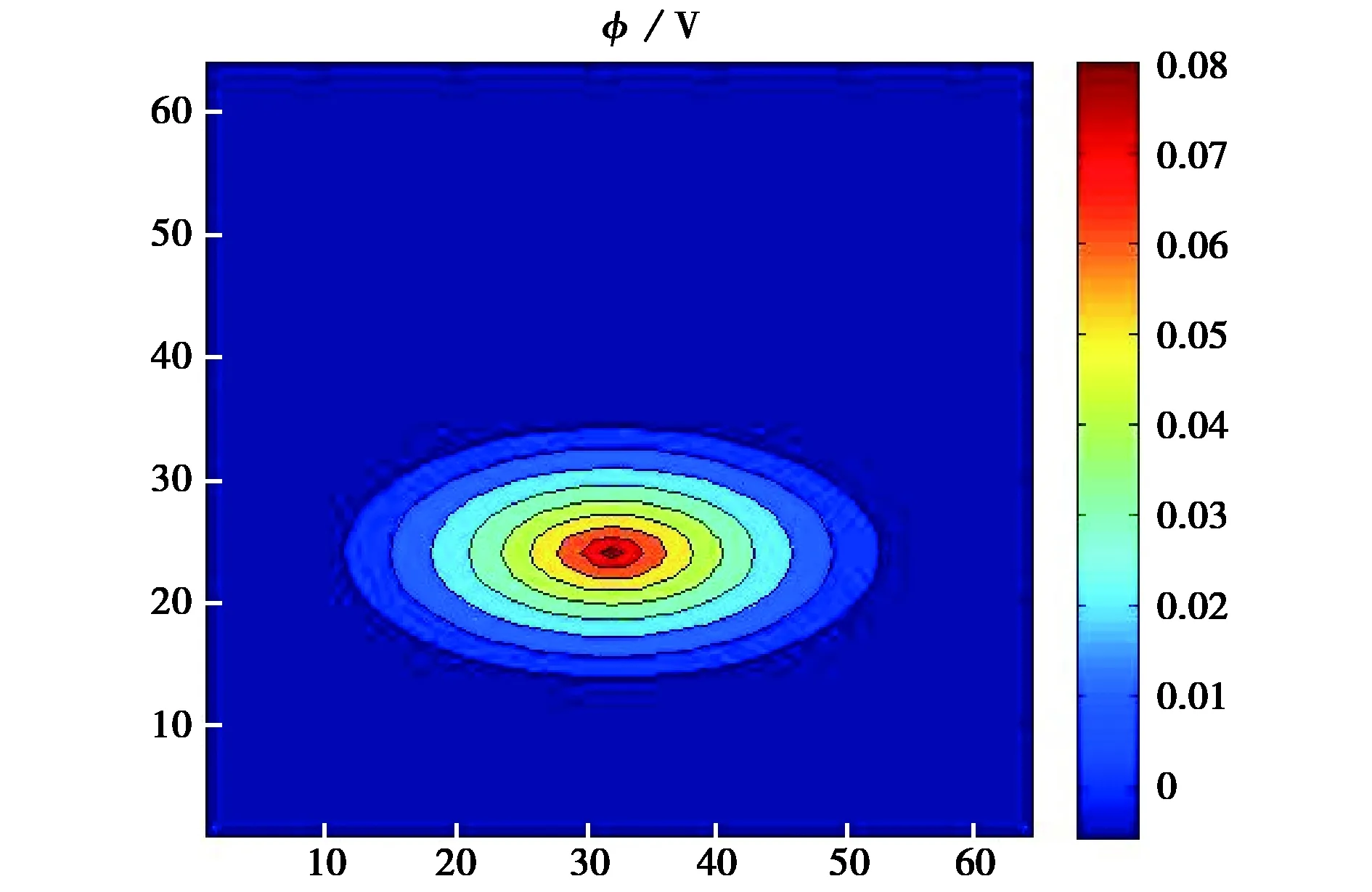
图3 牛顿下山法求解简单例的电势二维分布

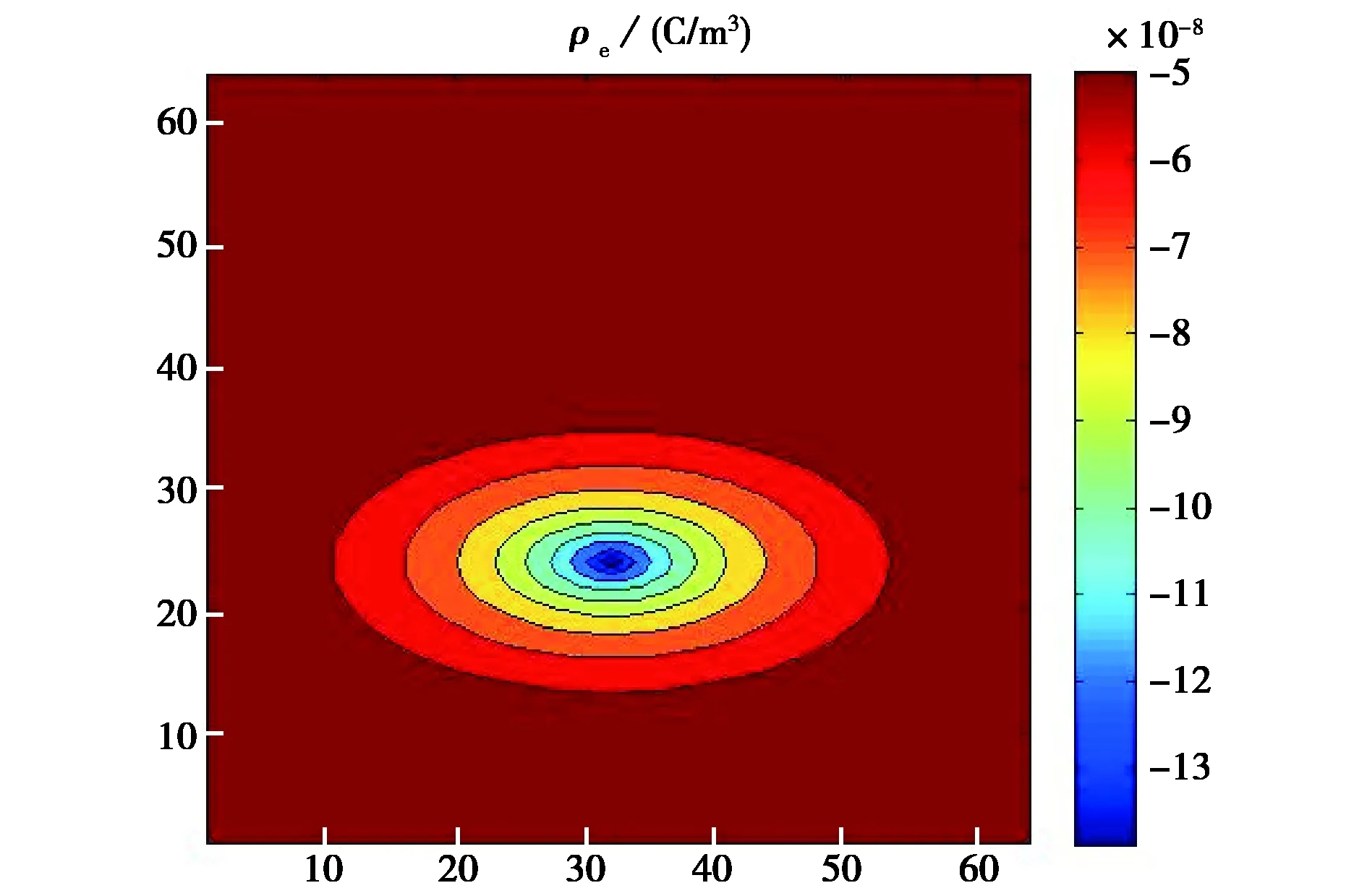
图4 牛顿下山法求解简单例的电子电荷密度二维分布

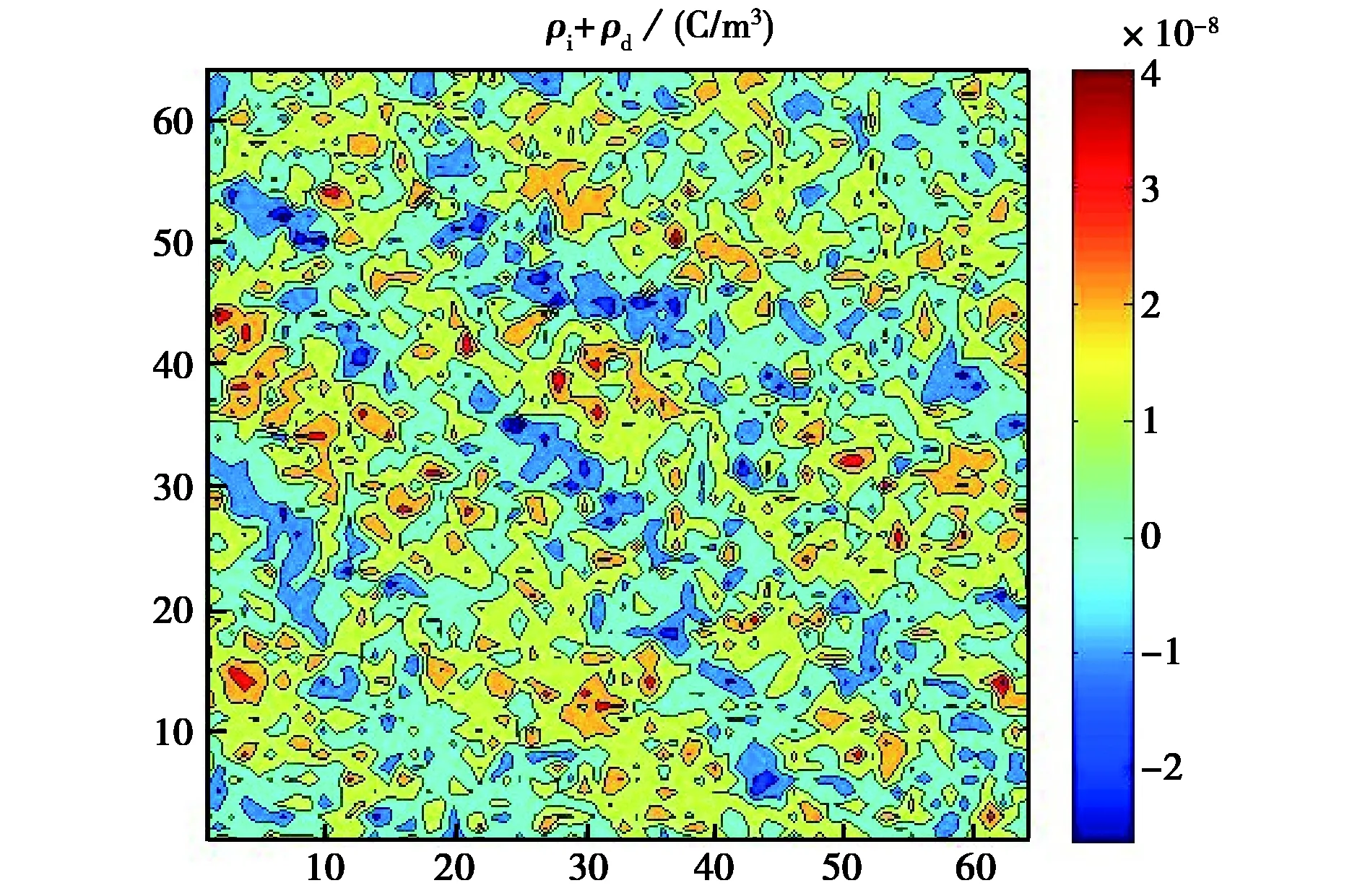
图5 尘埃粒子和离子总电荷密度二维分布复杂例

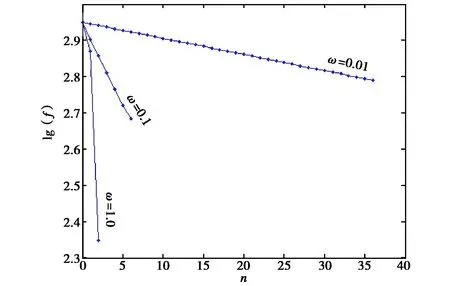
图6 不同下山因子下牛顿下山法求解复杂例的收敛过程

仍尝试运用牛顿下山法求解,得到不同下山因子下f值随迭代过程的变化结果,如图6所示.可以看到当ω=0.01、0.1和1.0时,迭代过程在最初均表现出了收敛性,且收敛速度随ω增大而加快. 然而,若干步后迭代均终止,表明牛顿下山法失败. 分析表明,迭代若干步后f′(φn)矩阵中少数元素计算值过小,导致由式(5)计算的电势值变化过大,直接违背了物理意义.从迭代过程的最初表现来看趋势还是不错的,因此，解决分母上的小值问题是关键. 可以考虑用固定值替代f′(φn),即所谓平行弦法. 可采用f′(φ0)来替代,有

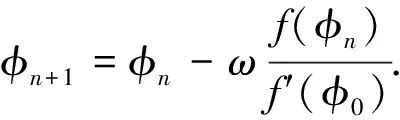
(8)

利用平行弦法计算得到不同下山因子下f值的变化过程,结果如图7所示.

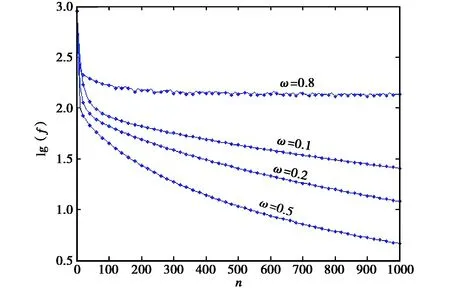
图7 不同下山因子下平行弦法求解复杂例的收敛过程

从图7分析可知,下山因子在一定范围内时(ω=0.1～0.5),平行弦法具有了收敛性,且迭代收敛速度随ω值增大而加快. 但下山因子取值过大时(ω=0.8),求解出现问题. 图8是ω=0.5、n=1 000时的电势二维分布计算结果. 再由式(2)得到电子电荷密度二维分布,如图9所示.

对于该复杂例,平行弦法的收敛速度是比较慢的. 图7中的结果表明,迭代次数达到1 000步时,收敛仍未完成. 同时,从解精度的预期来看,也不如简单例. 这是由两例中离子和尘埃粒子总电荷密度空间分布的复杂性差异造成的.

图8 平行弦法求解复杂例的电势二维分布

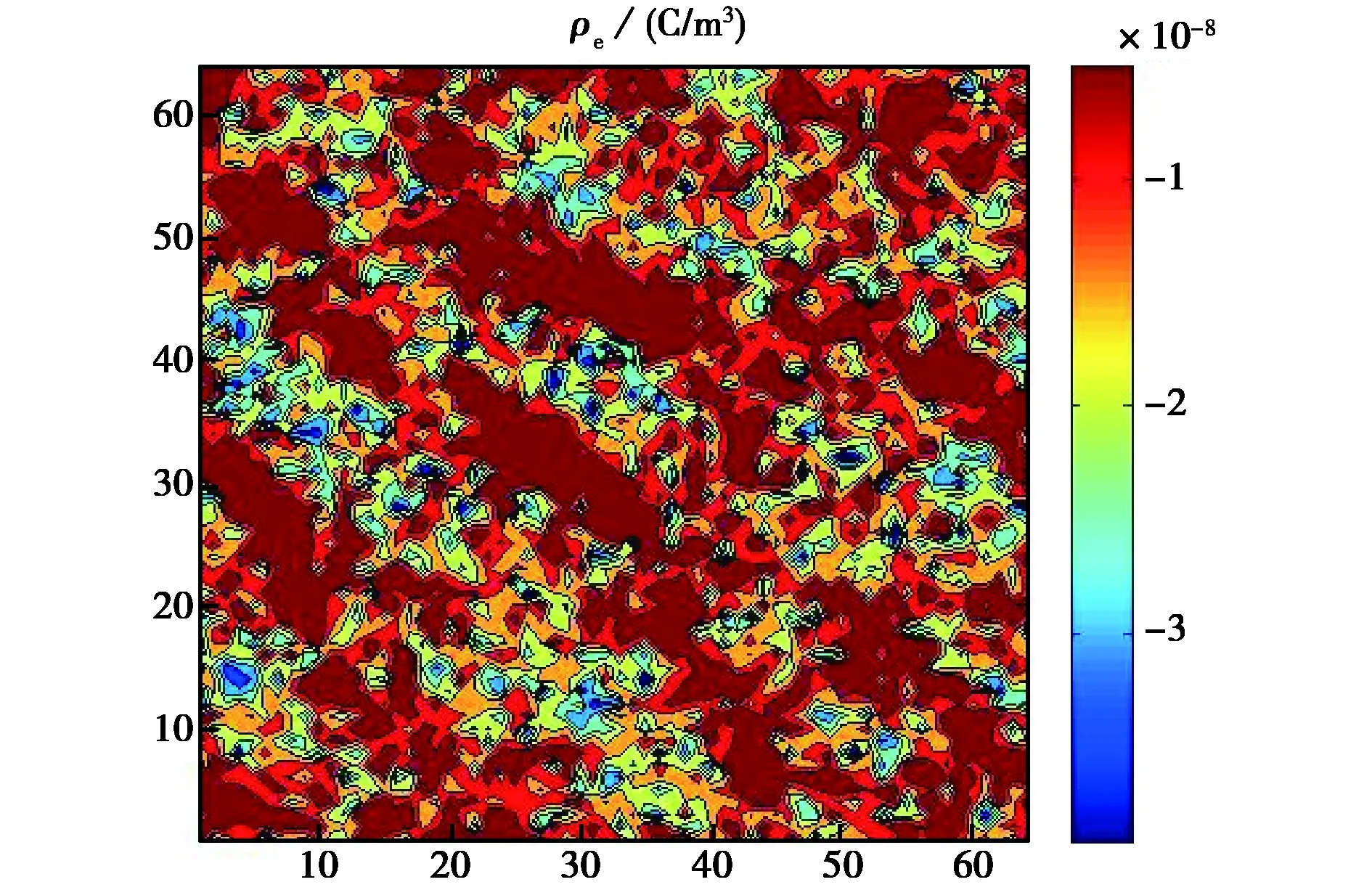
图9 平行弦法求解复杂例的电子电荷密度二维分布

3 结 论

尘埃等离子体领域工程实际问题中,经常采用混合模型处理不同的组分. 我们针对其中的一类情形研究了电荷-电势问题的求解. 具体情形为电子密度分布由波尔兹曼分布律决定,而电势场通过泊松方程由总电荷分布决定.

研究结果表明:对于简单的情况,牛顿下山法完全适用,且具有非常快的收敛速度和非常高的求解精度;而对于复杂的工程实际例子,牛顿下山法不再适用. 分析研究表明,平行弦法对此类工程实际问题具备可观的适用性. 下山因子取值在一定范围内时,迭代具备收敛性和稳定性,且收敛速度随下山因子的增大而加快. 当然,进一步的研究工作将在后续开展.

[1] TREFETHEN L N. Spectral Methods in MATLAB [M]. Philadelphia: Society for Industrial & Applied Mathematics, 2000.

[2] SHUKLA P K, MAMUN A A. Introduction to Dusty Plasma Physics[M]. London: IOP Publishing Ltd, 2002.

[3] 陈惠敏, 石雁祥, 苏金善, 等. 基于动力论的尘埃等离子体充电方程研究[J]. 电波科学学报, 2010, 25(5): 1005-1009.

CHEN Huimin, SHI Yanxiang, SU Jinshan, et al. Charging equation of dust plasmas based on kinetic theory[J]. Chinese Journal of Radio Science, 2010, 25(5): 1005-1009. (in Chinese)

[4] 石雁祥, 王 菊, 吴 健, 等. 对两种弱电离尘埃等离子体特征参量的定量估计[J]. 电波科学学报, 2008, 23(1): 95-99.

SHI Yanxiang, WANG Ju, WU Jian, et al. Characteristic parameters estimation of two weakly ionized dusty plasma[J]. Chinese Journal of Radio Science, 2008, 23(1): 95-99. (in Chinese)

[5] WINSKE D, YIN L, OMIDI N, et al. Hybrid Simulation Codes: Past, Present and Future—A Tutorial[M]. Berlin: Springer-Verlag, 2003: 136-165.

[6] CHAE G S, SCALES W A, GANGULI G, et al. Numerical model for low-frequency ion waves in magnetized dusty plasmas[J]. IEEE Trans Plasma Sci, 2000, 28(5): 1694-1705.

[7] HOLST M J. The Poisson-Boltzmann Equation-Analysis and Multilevel Numerical Solution (Monograph based on the Ph.D. Thesis: Multilevel Methods for the Poisson-Boltzmann Equation)[R]. Los Angeles: California Institute of Technology, 1994.

[8] 郑慧娆, 陈绍林, 莫忠息, 等. 数值计算方法[M]. 武汉:武汉大学出版社, 2002.