一类具有变时滞和脉冲的分层抑制细胞神经网络模型周期解的存在性

佘连兵

(六盘水师范学院数学系，贵州六盘水　530004)

一类具有变时滞和脉冲的分层抑制细胞神经网络模型周期解的存在性

佘连兵

(六盘水师范学院数学系，贵州六盘水530004)

摘要：应用不等式技巧、Mawhin迭合度理论研究了带分布连续时滞和脉冲的SICNNs模型周期解的存在性，得到系统至少存在一个ω周期解的充分条件.最后，通过一个例子验证了结论的正确性.

关键词：全局指数稳定；时滞细胞神经网络；周期解；迭合度理论

中图分类号：O 175.1

文献标志码：A

文章编号：1001-988Ⅹ(2015)03-0014-06

Existence of periodic solution for shunting inhibitory

cellular neural networks with variable delays and impulses

SHE Lian-bing

(Department of Mathematics,Liupanshui Normal College,Liupanshui 553004,Guizhou,China)

Abstract:This paper is devoted to the global existence of one periodic solution for shunting inhibitory cellular neural networks(SICNNs) with time varying and continuously distributed delays and impulses by using inequality techniques and the Mawhin’s continuation theorem，a sufficient condition that the system there has at least a ω-periodic solution is given.Finally,an example is provided to show the correctness of our analysis.

Key words:globally exponential stability;delayed cellular neural networks;periodic solution;Mawhin’s continuation theorem

0引言

近些年，许多领域对分层抑制细胞神经网络模型产生了浓厚的兴趣[1,2]，本文研究如下SICNNS模型周期解的存在性和全局指数稳定性：

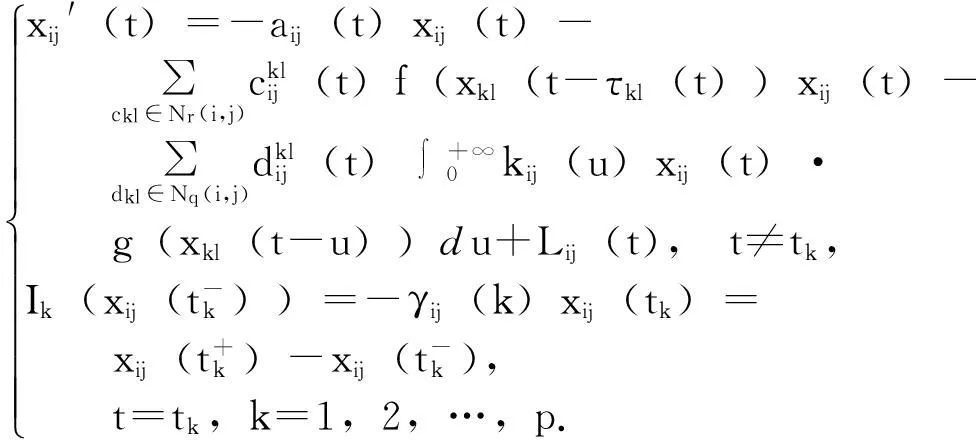
这里，i=1,2,…,n,j=1,2,…,m;aij∈C([0,+∞),R+)表示细胞活性的被动衰变；Cij表示在格子(i,j)处的细胞；xij表示神经细胞Cij的状态；远域区Nr(i,j)定义为

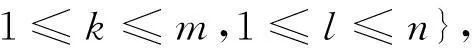
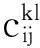
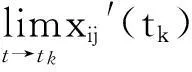
本文我们做如下假设：

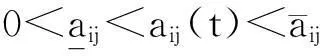
(H2)f,g∈C(R,R)满足利普希茨条件，且存在利普希茨常数Lf,Lg>0，使得

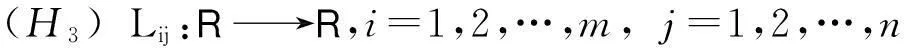
(H4)对x∈R,存在正常数Mf,Mg>0,使得

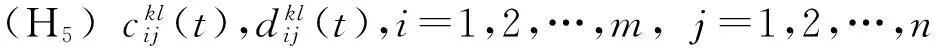
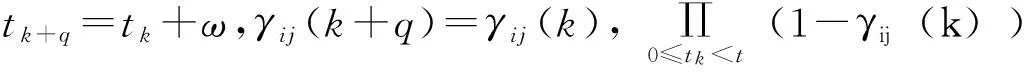
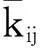
(H8) τkl(t)是以ω为周期的有界连续函数.

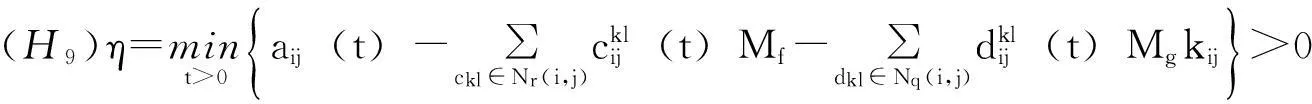
为方便起见，记

1定义和引理

首先引入一些基础知识和引理.令ω=mn,x(t)=(x11(t),…,xm1(t),…x1n(t),…xmn(t))T,用Ω表示所有周期函数构成的集合.

定义1若对∀t≥0，存在常数α>0和β>0，使得系统(1)的周期解x*满足

则称系统(1)的解x*是全局指数稳定的，其中

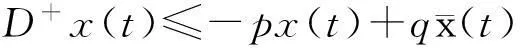
下面考虑非脉冲带时滞的微分方程

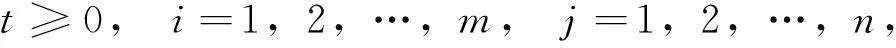
(2)

初始条件为

其中φij(t)定义如上.

引理2假设条件(H6)成立，则

( i )如果y(t)=(y11(t),…,ym1(t),…,y1n(t),…,ymm(t))是方程(2)的解，则

是系统(1)的解.

(ii)如果x(t)=(x11(t),…,xm1(t),…,x1n(t),…,xmm(t))是系统(1)的解，则

是方程(2)的解.

参考文献引理2的证明可以[6]定理2.1的证明.

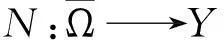
2周期解的存在性

为方便起见，记

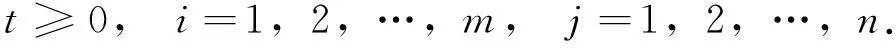
定理1假设条件(H1)～(H9)成立，则系统(1)至少有一个以ω为周期的正解.

证明根据引理2，只需证明非脉冲时滞方程(2)有一个以ω为周期的解.为了应用引理3证明方程(2)解的存在性，令

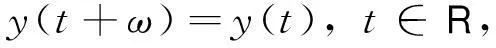
其中y的模定义为

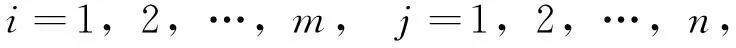
则Y和Z为Banach空间.令

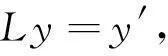
显然，

dim KerL=mn=codim ImL.

因此，ImL是闭集，L是零指标的Fredholm映射.易知，P、Q是连续映射，且满足

ImP=KerL,ImL=KerQ=Im(I-Q).

因此

KP(I-Q)Ny=

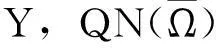
下面寻找一个合适的有界开集Ω⊂Y.对应于算子方程Lx=λNx,λ∈(0,1)，可得到

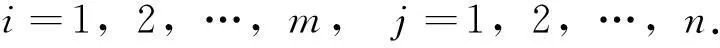
(3)

假设对某个λ∈(0,1)，y=(y11,…,ym1,…,y1n,…,ymn)T∈Y是系统(3)的解，将yij(t)yij′(t)从0到ω积分可得

因此

由假设条件(H1),(H3～(H5),(H7),(H9)可知

其中

所以

(4)

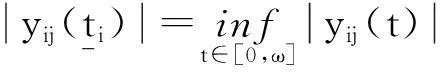
因此

(5)

(6)

另一面，由(3)式和条件(H3)～(H5),(H7)可得

结合(4)式可得

(7)

由(6)和(7)式可得

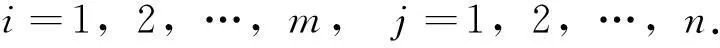
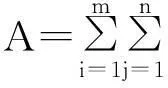
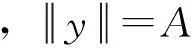
其中

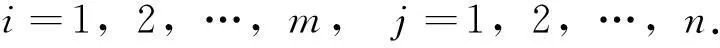
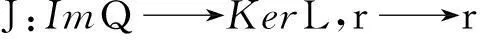
deg{JNQ,Ω∩KerL,0}=

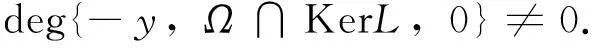
因此，引理3的条件(b)满足，从而方程(2)至少有一个以ω为周期的解，所以系统(1)至少有一个以ω为周期的解.】

3例子

下面给出一个例子验证定理1的结论.令m=n=3,f(x)=0.4sinx，g(x)=0.5[1-exp(-x)]/[1+exp(-x)]，易知，Mf=0.4,Mg=0.5,Lf=0.4,Lg=0.5,f(0)=g(0)=0.考虑脉冲微分方程

容易得到

(3.6458,4.7234,4.1303,3.9394,2.9594,

3.8399,2.9847,3.2345,3.9932)T，

(0.2548,0.1234,0.1303,0.3394,0.2594,

0.2399,0.1847,0.2345,0.3932)T,

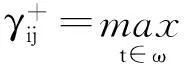
[1]LIUYi-guang,YOUZhi-sheng,CAOLi-ping.Almostperiodicsolutionofshuntinginhibitorycellularneuralnetworkwithtinevaryingandcontinuouslydistributeddelay[J].Physics LettersA,2007,364(1)：17-28.

[2]LIUBing-wen,HUANGLi-huang.Almostperiodicsolutionsofshuntinginhibitorycellularneuralnetworkwithtime-varyingdelays[J].Applied Mathematics Letters,2007,20(1):70-74.

[3]CAOJin-de.Asetofstabilitycriteriafordelaycellularneuralnetworks[J].IEEE Trans Circuits Syst Ⅰ,2001,48:494-8.

[4]LIYong-kun.GlobalexponentialstabilityofBAMneuralnetworkswithdelaysandimpulses[J].Chaos,Solitons & Fractals,2005,24(1):279-285.

[5]LIYong-kun,XINGZhi-wei.ExistenceandglobalexponentialstabilityofperiodicsolutionofCNNswithimpulses[J].Chaos,Solitons & Fractals,2007,33(5):1686-1693.

[6]LIYong-kun,XINGWen-ya,LULing-hong.Existenceandglobalexponentialstabilityofperiodicsolutionofaclassofneuralnetworkswithimpulses[J].Chaos,Solitons & Fractals,2006,27(2):437-445.

[7]GAINSRE,MAWHINJL.Coincidence Degree and Nonlinear Differential Equation[M].Berlin:Springer,1977.

[8]LIDing-shi,WANGXiao-hu,XUDao-yi.Existenceandglobalp-exponentialstabilityofperiodicsolutionforimpulsivestochasticneuralnetworkswithdelays[J].Nonlinear Anal Hybrid Syst,2012,6(3):847-858.

[9]LIYong-kun,SHUJiang-ye.Anti-periodicsolutionstoimpulsiveshuntinginhibitorycellularneuralnetworkswithdistributeddelaysontimescales[J].Commun Nonlinear Sci Numer Simul,2011,16(8):3326-3336.

[10]LIYong-kun,CHAOWang.Almostperiodicsolutionsofshuntinginhibitorycellularneuralnetworksontimescales[J]. Commun Nonlinear Sci Numer Simul,2012,17(8):3258-3266.

(责任编辑马宇鸿)

作者简介：佘连兵(1981—),男，河南信阳人,讲师,硕士.主要研究方向为微分方程定性理论.

基金项目:贵州省科学技术基金资助项目(LKZS[2011]2117,LKZS[2012]11,LKZS[2012]12,LKZS[2014]22)

收稿日期：2014-09-17;修改稿收到日期:2014-10-10

E-mail:shelianbing@163.com