基于非参数检验的商业银行资产价格多变结构点研究
姚德权+黄学军+易琳

摘 要:准确判断商业银行资产价格的变化规律是商业银行风险评估和预警的前提。以改进的多变结构点非参数检验方法为基础,实证检验2007~2013年上市商业银行资产价格的变结构点,结果表明:商业银行资产价格在样本期产生了多个均值变结构点和方差变结构点,且系统因素、行业因素和商业银行特质因素均可能会导致商业银行资产价格变结构点的出现。
关键词: 多变结构点;非参数检验;时间序列分解;商业银行资产价格
中图分类号: F830 文献标识码: A 文章编号:1003-7217(2014)06-0008-05
一、引 言
商业银行是金融市场的重要组成部分,在以间接融资为主的经济体系内,商业银行的作用更为明显,截至2013年年末,我国银行业金融资产总额达到了151.35万亿元,远远超出2013年GDP。银行业的健康发展直接影响到金融市场和实体经济的健康发展,因此,学界和业界一直都重视其运营的风险,特别是在次债危机之后,一些大型银行也陷入了金融风险的泥潭,并且银行危机加剧了金融危机的破坏程度,这使得国内外对商业银行风险的关注度进一步提升。
准确判断商业银行资产市场价值的变化,是商业银行金融风险评估和预警的基础。Gropp等[1], 苏健等[2], 以及吴恒煜[3]等分别以商业银行资产市场价值为计算基础,设计了或有权益方法(Contingent Claims Analysis, CCA)对商业银行风险进行度量,实证研究结果表明,资产市场价值的变化是商业银行经营的结果,并隐含了其资产价值未来变化信息,研究认为资产市场价值变化具有较强的前瞻性(Forword Looking),因而能有效判断商业银行的风险。与此同时,一些文献探讨了资产价值的时序变化特征,资产市场价值具有时间连续性,其资产价格收益率应具有平稳特征。Kasman等分析了银行资产市场价值的变化规律[4];梁海鸥和玄永生[5]、彭伟在连续时间金融的条件下分析了上市商业银行股票日收益风险[6];彭建刚和马亚芳从系统重要性角度,通过评价商业银行资产价值等信息分析了银行风险的变化过程[7]。
近年来,不少研究如王珏等[8]、罗长青等[9]等文献均表明资产价值并不满足平稳特征,而是会出现“突变”现象,从某一时间点开始,时间序列模型参数会发生变化,也就是资产价格出现了突变,而这类变点称之为结构变点。陈希孺给出了一般的结构变点研究方法[10],韩四儿对金融市场上常用的ARCH 过程的多变点问题进行了研究[11],Tsay在建模的过程检测结构变点的位置与跳跃度[12],郑仲民对金融资产价格跳跃行为研究[13],然而,这些方法对数据附加了一些分布假设条件或者模型假设条件,使得应用范围比较局限。而且在结构变点检测过程中,需要估计分布或模型的参数,使得计算量增大。Wu和Zhao提出了一种非参数方法检测均值变点[14],这种方法的优点是计算较快,但是Wu和Zhao的检验统计量的极限分布是在只有一个均值变点的假设条件下给出的, 它不能用于多个均值变结构点的情形,更不能用于方差变结构点的情形,特别是多个方差变结构点的情形,因此,在对时间序列变结构点进行检验时,需要对已有方法进行改进,以便能够一次性识别均值和方差多个变结构点。
受宏观宏观经济的波动,或国家重要政策、重大信息和公告(如IPO,兼并收购等)的发布等因素的影响,商业银行资产价格在近似连续的时间内很有可能会出现较大幅度的波动,这种由突发信息引起对商业银行资产价格(收益)及波动过程所造成的冲击现象即银行资产价格的“突变”。而且,在一段时间内,商业银行资产价值可能出现连续突变现象,而传统的检验方法难以一次性检出多个变结点。商业银行资产价格的突变现象直接影响金融资产收益波动率的估计和预报的准确程度,进而对商业银行风险管理产生重大影响,传统的计量模型和方法也就需要进行相应的调整。
财经理论与实践(双月刊)2014年第6期2014年第6期(总第192期)姚德权,黄学军:基于非参数检验的商业银行资产价格多变结构点研究
鉴此,本文基于Wu和Zhao的检验方法,提出商业银行资产价格均值和方差的多变结构点检验方法,并基于该方法对商业银行变结构点进行实证检验,从而进一步发现商业银行资产价格变化的规律和特征。
二、商业银行资产价格多变结构点非参数检验模型的构建
(一)商业银行资产价格变结构点检验模型的基本设定
商业银行的资产价格随时会发生变化,设定资产价格的平均值在m个时刻发生突变,变化的时刻为k1,k2,…,km,同时设定资产价格的方差在w个时刻发生突变,时刻为s1,s2,…,sw,参考Wu和Zhao的研究[14],将变结构资产价格模型设定为:
xi=μ1+rt 1≤t≤k1
μ2+rt k1+1≤t≤k2
… …
μm+1+rt km+1≤t≤n(1)
其中k1,k2,…,km为m个均值变结构点。假设rt~N(0,σ2t), 那么:
σ2t=v1 1≤t≤s1
v2 s1+1≤t≤s2
… …
vw+1 sw+1≤t≤(2)
其中s1,s2,…,sw为w个方差变结构点。进一步,可以假设数据在每两个变结构点之间服从具体的分布或模型,本文选取的模型为GARCH模型,然后对模型进行估计。对于一个给定的资产价格和给定的区间长度Ln,定义:
D=maxtn≤i≤n-tnDi
其中:
Di=1ln∑ln+it=i+1xt-1ln∑it=i-ln+1xt
(ln≤i≤n-ln)(3)
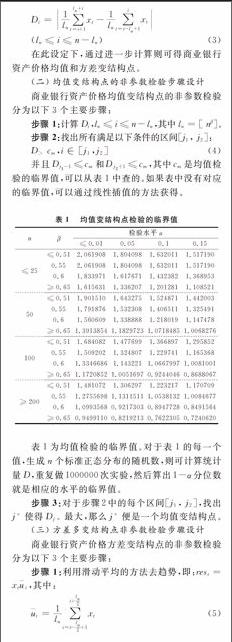
在此设定下,通过进一步计算则可得商业银行资产价格均值和方差变结构点。
(二)均值变结构点的非参数检验步骤设计
商业银行资产价格均值变结构点的非参数检验分为以下3个主要步骤:
步骤 1:计算Di,ln≤i≤n-ln,其中ln =[ nβ]。
步骤 2:找出所有满足以下条件的区间[j1, j2]:
D>cm,i∈[j1,j2](4)
并且Dj1-1≤cm和Dj2+1≤cm,其中cm是均值检验的临界值,可以从表1中查的。如果表中没有对应的临界值,可以通过线性插值的方法获得。
表1 均值变结构点检验的临界值
n
β
检验水平α
≤0.01
0.05
0.1
0.15
≤25
≤0.51
2.061908
1.804098
1.632011
1.517190
0.55
2.061908
1.804098
1.632011
1.517190
0.6
1.833971
1.617671
1.432382
1.368953
≥0.65
1.615631
1.336207
1.201281
1.108521
50
≤0.51
1.901510
1.643275
1.524871
1.442003
0.55
1.791876
1.532308
1.406511
1.325491
0.6
1.560609
1.338888
1.218019
1.147478
≥0.65
1.3913854
1.1829723
1.0718485
1.0068276
100
≤0.51
1.684082
1.477699
1.366897
1.295852
0.55
1.509202
1.324807
1.229741
1.165368
0.6
1.3346686
1.143221
1.0667997
1.0081001
≥0.65
1.1720852
1.0051697
0.9244046
0.8688067
≥200
≤0.51
1.481072
1.306297
1.223217
1.170709
0.55
1.2755698
1.1311511
1.0538132
1.0084677
0.6
1.0993568
0.9217303
0.8947728
0.8491564
≥0.65
0.9499110
0.8219213
0.7622305
0.7240620
表1为均值检验的临界值。对于表1的每一个值,生成n个标准正态分布的随机数,则可计算统计量D,重复做1000000次实验,然后算出1-α分位数就是相应的水平的临界值。
步骤 3:对于步骤2中的每个区间[j1, j2],找出j*使得Dj*最大,那么j*便是一个均值变结构点。
(三)方差多变结构点非参数检验步骤设计
商业银行资产价格方差变结构点的非参数检验分为以下3个主要步骤:
步骤 1:利用滑动平均的方法去趋势,即:rest=xti,其中:
t=1ln∑i+ln2i=t-ln2+1xt(5)
步骤 2:标准化rt ,即:rest=rest/sd(res), 其中sd(res)表示rest的标准差。
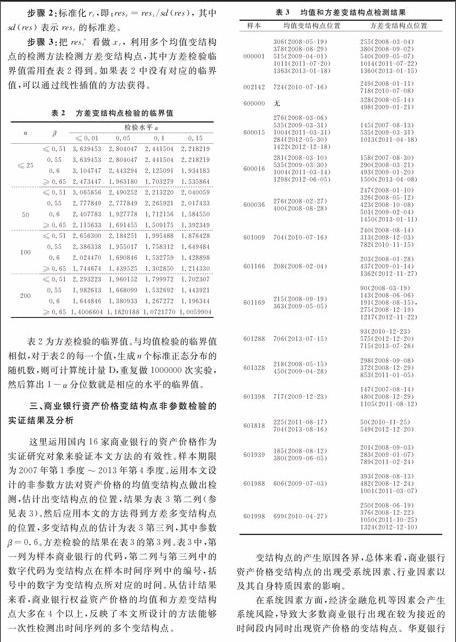
步骤 3:把res*t看做xt, 利用多个均值变结构点的检测方法检测方差变结构点,其中方差检验临界值需用查表2得到。如果表2中没有对应的临界值,可以通过线性插值的方法获得。
表2 方差变结构点检验的临界值
n
β
检验水平α
≤0.01
0.05
0.1
0.15
≤25
≤0.51
3.639453
2.804047
2.441504
2.218219
0.55
3.639453
2.804047
2.441504
2.218219
0.6
3.104747
2.443294
2.125091
1.934183
≥0.65
2.473447
1.963180
1.703279
1.535864
50
≤0.51
3.065856
2.490252
2.213220
2.040059
0.55
2.777849
2.777849
2.265921
2.017433
0.6
2.407783
1.927778
1.712156
1.584550
≥0.65
2.115633
1.691455
1.509175
1.392349
100
≤0.51
2.656300
2.184251
1.995488
1.876428
0.55
2.386338
1.955017
1.758312
1.649484
0.6
2.024470
1.690846
1.532759
1.428898
≥0.65
1.744674
1.439525
1.302850
1.214330
200
≤0.51
2.293223
1.960152
1.799972
1.702307
0.55
1.982613
1.668099
1.532692
1.443921
0.6
1.644846
1.380933
1.267272
1.196344
≥0.65
1.4006604
1.1820188
1.0721770
1.0059904
表2为方差检验的临界值。与均值检验的临界值相似,对于表2的每一个值,生成n个标准正态分布的随机数,则可计算统计量D,重复做1000000次实验,然后算出1-α分位数就是相应的水平的临界值。
三、商业银行资产价格变结构点非参数检验的实证结果及分析
这里运用国内16家商业银行的资产价格作为实证研究对象来验证本文方法的有效性。样本期限为2007年第1季度~2013年第4季度。运用本文设计的非参数方法对资产价格的均值变结构点做出检测,估计出变结构点的位置,结果为表3第二列(参见表3)。然后应用本文的方法得到方差多变结构点的位置,多变结构点的估计为表3第三列,其中参数β=0.6。方差检验的结果在表3的第3列。表3中,第一列为样本商业银行的代码,第二列与第三列中的数字代码为变结构点在样本时间序列中的编号,括号中的数字为变结构点所对应的时间。从估计结果来看,商业银行权益资产价格的均值和方差变结构点大多在4个以上,反映了本文所设计的方法能够一次性检测出时间序列的多个变结构点。
表3 均值和方差变结构点检测结果
样本
均值变结构点位置
方差变结构点位置
000001
306(20080519)
378(20080829)
515(20090401)
1011(20110720)
1363(20130118)
255(20080304)
380(20080902)
540(20090507)
1014(20110722)
1360(20130115)
002142
724(20100716)
249(20080111)
718(20100708)
600000
无
328(20080514)
498(20090121)
600015
276(20080306)
535(20090331)
1004(20110331)
284(20120530)
1422(20121218)
145(20070813)
535(20090331)
1013(20110418)
600016
281(20080310)
535(20090330)
1004(20110314)
1298(20120605)
158(20070830)
290(20080321)
493(20090120)
1500(20130408)
600036
276(20080227)
400(20080828)
247(20080110)
326(20080512)
423(20081008)
501(20090204)
1450(20130111)
601009
704(20100716)
240(20080814)
313(20081203)
782(20101115)
601166
208(20080204)
203(20080128)
437(20090114)
1362(20121127)
601169
215(20080919)
363(20090505)
90(20080319)
143(20080606)
191(20080815),
275(20081219)
1217(20121122)
601288
706(20130715)
93(20101223)
575(20121220)
715(20130726)
601328
218(20080515)
450(20090428)
298(20080908)
372(20081229)
853(20110105)
601398
717(20091223)
147(20070814)
480(20081229)
1105(20110812)
601818
225(20110817)
704(20130816)
50(20101125)
549(20121220)
601939
185(20080812)
380(20090605)
201(20080903)
283(20090107)
789(20110224)
601988
606(20090703)
393(20080813)
482(20081224)
1001(20110307)
601998
699(20100427)
250(20080619)
376(20081222)
1050(20111025)
1324(20121210)
变结构点的产生原因各异,总体来看,商业银行资产价格变结构点的出现受系统因素、行业因素以及其自身特质因素的影响。
在系统因素方面,经济金融危机等因素会产生系统风险,导致大多数商业银行出现在较为接近的时间段内同时出现资产价格的变结构点。华夏银行(600015)、民生银行(600016)等在2007年8月左右出现了权益资产价值的变结构点,在此期间,贝尔斯登、巴黎银行瑞穗银行等出现了较大的次贷投资损失。虽然国内银行参与次债投资的程度不深,但是金融危机所带来的恐慌也影响了投资者对银行的预期,并在一定程度上动摇了对银行的信心,从而导致已上市的银行权益资产价值的波动出现了变化,并导致商业银行权益资产价值变结构点的出现。2007年末~2008年初,大多数商业银行的权益资产价值均出现了均值和方差变结构点,这一时期正是次债危机愈演愈烈的阶段,2007年末~2008年初,市场流动性压力急剧增加。至2008年3月,美国第五大投资银行贝尔斯登濒临破产,而美国房利美和房地美两大放贷机构宣布亏损110亿美元,次债危机逐渐演化成全球经融危机,并导致世界主要经济体陷入衰退周期。在危机冲击和风险传染影响下,国内企业的景气指数也逐渐下降,外部环境的严重恶化,导致商业银行风险提高,并且这种风险变化反映到了其在证券市场的资产价格,样本商业银行在此期间均出现了变结构点。2012年11月8日~14日,中国共产党第十八次全国代表大会成功召开,对政治经济产生了较为深远的影响,在深化金融体制改革方面,要求进一步深化金融改革,加快推进利率和汇率市场化改革,并逐步实现资本项目可兑换和加快民间金融机构的发展。2012年12月,制造业PMI 指数为50.6%,高于50%的荣枯线,显示制造业需求在上升。规模以上工业增加值同比增长10.3%,带动全年增长10.0%,2012 年12月,全国规模以上工业企业累计利润在12月份实现转负为正。一系列经济数据表明宏观经济“最差的时候已经过去”,同时,新一轮金融改革的启动标志着银行业发展将迎来一个新的环境。
行业监管政策等行业因素也是商业银行变结构点产生的原因之一。如,2008年底~2009年年初,各商业银行资产价值均值和方差又一次先后出现系统性的变结构点。从2008年11月27日起,下调金融机构一年期人民币存贷款基准利率各1.08个百分点,其他期限档次存贷款利率作相应调整,同时下调央行再贷款再贴现利率。从2008年12月5日起,下调工商银行、农业银行、中国银行、建设银行、交通银行和邮政储蓄银行等大型存款类金融机构人民币存款准备金率1个百分点,下调中小型存款类金融机构人民币存款准备金率2个百分点。此轮降息和调准超出市场预期,行业监管政策的变化导致了大多数银行的权益资产价值出现了变结构点。从表3也可以发现,商业银行资产价格变结构点出现的时间较为接近,这反映出系统因素和行业因素等共同因素是商业银行资产价格变结构点出现的主因。
此外,商业银行特质因素也会导致其权益资产变结构点的出现。如深发展(自2012年7月27日起变更为平安银行股份有限公司,简称“平安银行”)在2009年5月7日出现资产价值的变结构点,深发展(000001)与中国平安人寿保险股份有限公司(简称“平安寿险”)于2009年6月8日停牌,并于该月12日签署了《深圳发展银行股份有限公司和中国平安人寿保险股份有限公司之股份认购协议》,公司拟向中国平安人寿保险股份有限公司非公司发行不少于3%亿股,但不超过5.85亿股人民币普通股,该重组方案实施后,中国三大保险公司之一平安集团旗下的平安人寿将成为了该行新的战略投资者,深发展也更名为平安银行,市场投资者对此次股权结构的重大变化提前做出了市场反应,导致其权益资产价值出现了变结构点。该银行在2011年7月24日出现了资产价值的变结构点,其后深发展在7月28日晚发布公告称,深发展与平安集团的重大资产重组工作已经完成,重大资产重组完成以后,中国平安及中国平安控股子公司中国平安人寿保险股份有限公司合计持有公司52.38%,成为公司的控股股东,该银行由重组期进入重组后的稳定发展期,市场对此次重大事件的反应提前了5个交易日,在24日即出现了资产价值的变结构点。
值得关注的是,对于系统因素和行业因素,商业银行的变结构点可能出现在重大事件之前或之后,而对特质因素的反应,则一般出现在商业银行重大事件公布日之前,如宁波银行(002142)在2010年7月8日出现了变结构点,而在2010年7月13日,宁波银行发布的《宁波银行中期业绩修正公告》将预计归属于上市公司股东的净利润与上年同期相比增长幅度调整至70%~80%,并称总行大厦拆迁将获得拆迁收入4.05 亿元,该事件对宁波银行权益资产价值起到了一定的提振作用。华夏银行(600015)在2011年4月18日出现了变结构点,而在4月28日,华夏银行公布实施定向增发,增发数量185919.746万股,增发金额达208亿。民生银行于2013年4月8日出现了变结构点,在同年4月24日和25日,该行分别发布第一季报和《关于公开发行有锁定期的A股可转换债券上市交易的提示性公告》等对股权价值有重要影响的信息,根据该季报和公告的时间节点,也可以发现商业银行资产价值对特质因素的反应时间一般出现在其重大事件公布之前。
四、结论及启示
基于改进后的非参数检验方法,本文对商业银行资产价格变结构特征进行了实证检验,实证研究表明,商业银行资产价格存在较为显著的变结构特征,系统因素、行业因素和商业银行特质因素均可能会导致商业银行资产价格变结构点的出现,且系统因素和行业因素在样本期内对估计出的变结构点起主导作用。通过以上实证结论带来以下启示:(1) 本文所构建的多变结构点非参数检验方法适用于检测商业银行资产价格的变结构点,此外,对于其他时间序列的变结构点检验,也可以尝试运用该非参数检验方法。(2) 基于商业银行资产价格的风险度量模型和管理模型需考虑资产价格的变结构特征,否则有可能出现模型设定偏差,从而会导致模型准确度和风险预警效能下降。(3) 商业银行在进行风险承担管理和风险预警时,尤其要注意系统因素和行业因素对商业银行资产价格的影响。
参考文献:
[1]Gropp R, Vesala J, Vulpes G. Equity and bond market signals as leading indicators of bank fragility[J]. Journal of Money, Credit and Banking, 2006, 38(2): 399-428.
[2]苏健, 姬明, 钟恩庚. 我国银行业整体风险的度量——基于CCA方法的定量测算[J]. 金融理论与实践, 2012, (10): 12-17.
[3]吴恒煜, 胡锡亮, 吕江林. 我国银行业系统性风险研究——基于拓展的未定权益分析法[J]. 国际金融研究, 2013, (7): 107-122
[4]Kasman S, Vardar G, Tun G. The impact of interest rate and exchange rate volatility on banks' stock returns and volatility: Evidence from Turkey[J]. Economic Modelling, 2011, 28(3): 1328-1334
[5]梁海鸥,玄永生. 中国银行股票价格波动的ARCH模型分析[J]. 中国证券期货, 2011, (10): 21-22.
[6]彭伟. 我国上市商业银行股票日收益风险价值研究——基于AR、HAR和MIDAS模型的分析[J]. 金融监管研究, 2013, (3): 89-103
[7]彭建刚,马亚芳. 基于系统整体性的商业银行系统重要性评估方法[J]. 财经理论与实践,2013,(6): 2-7
[8]王珏, 胡赟, 张迎新. 资产价格时间序列的BLS结构突变点检验及其对历史研究的意义[J]. 中国人民大学学报, 2012, (4): 72-79
[9]罗长青, 朱慧明, 欧阳资生. 跳跃—扩散条件下信用风险相关性度量的变结构Copula模型[J]. 中国管理科学, 2014, (3): 1-12
[10]陈希孺. 变点统计分析简介[J]. 数理统计与管理, 1991, 10(2): 52-59.
[11]韩四儿, 田铮, 武新乾. 一类股市波动性预测模型的多变检验点[J], 系统工程理论与实践2006, (3): 94-101.
[12]Tsay R S. Outliers, level shifts, and variance changes in time series[J]. Journal of Forecasting, 1988, (7): 1–20.
[13]郑仲民. 金融资产价格跳跃行为研究[D] .天津;天津大学,2011.
[14]Wu W B, Zhao Z B. Inference of trends in time series[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2007, 69(2): 391–410
(责任编辑:钟 瑶)

