Comprehensive Evaluation of Economic Indicators in Guangxi Economic Zone Based on Parallel Analysis

Guangdong ZENG，Chunxiang ZHAO

College of Science，Engineering University of CAPF，Xi'an 710086，China

1 Introduction

The assessment and prediction of economic development trend in economic zone is of important practical significance to government departments．When we conduct a comprehensive evaluation of economy in one region，it is difficult to choose evaluation indicator system and integrate the indicators．This requires a sound analysis method to determine the important comprehensive indicators．In this paper，according to Guangxi Statistical Yearbook（2013），we select 8 key indicators（land area X1；permanent population at the end of year X2；regional GDP X3；social fixed asset investment X4；public budget revenue X5；public budget expenditure X6；total retail sales of social consumer goods X7；import and export X8）to reflect economic conditions．The specific indicators are shown in Table 1．

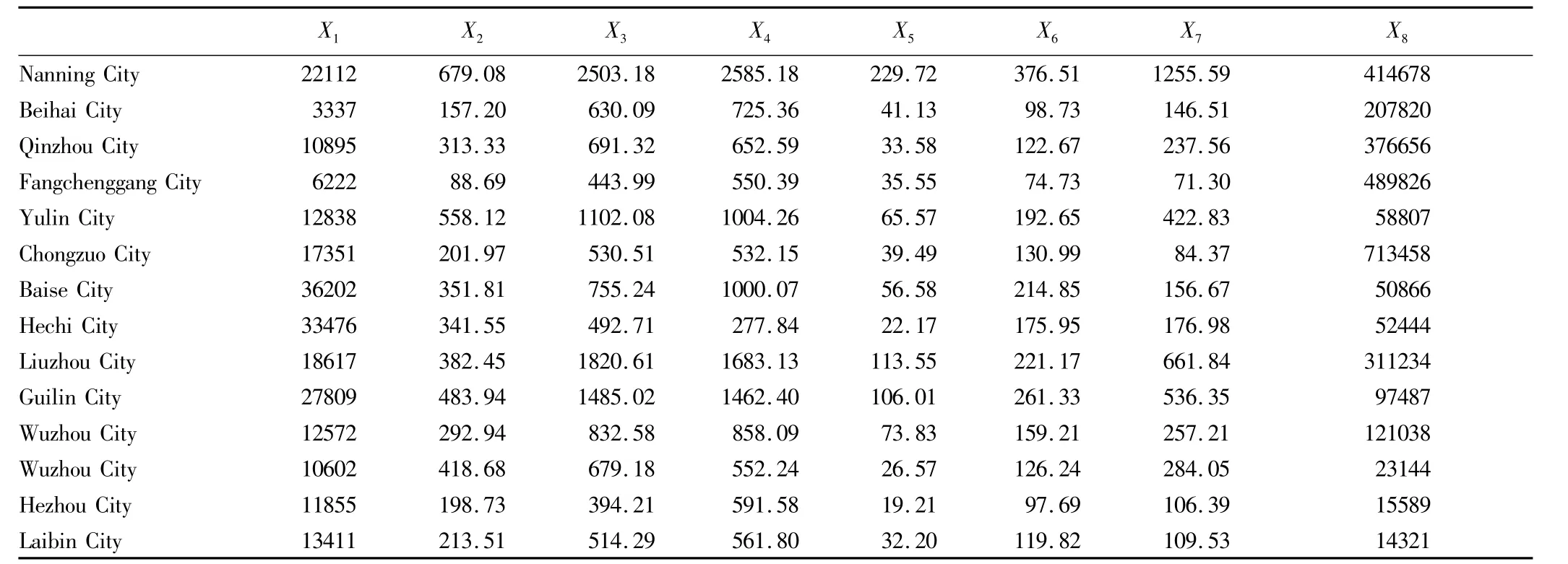
Table 1 The major economic indicators of Guangxi's economic zones in 2013

2 Basic principles of parallel analysis and principal component analysis

Principal component analysis（PCA）is a statistical procedure that uses an orthogonal transformation to convert a setofobservations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components．The information in principal component refers to the variability of the variable．The greater the variability of the variables，the greater the amount of information．In the principal component analysis，standard deviation or variance is used to represent variability．Assuming X＝（X1，…，Xp）Tis p-dimensional random variable．The composite indicator of X［Y1，…，Yk（k≤p）］is determined as follows：（i）calculating the eigenvalue of the covariance matrix of X（Σ ），denoted as：λ1≥λ2≥…≥λk＞0，λk＋1＝… ＝λp＝0；（ii）calculating the unit eigenvectorγi（i＝1，2，…，k）thatλicorresponds to，and requiring orthogonality；（iii）getting principal component i：Yi＝γiX，i＝1，2，…，K．Obviously，for any two principal components of X，it is easy to verify：

The weighted sum of principal components is calculated，and the new composite indicators are established．The weight of the principal components is determined based on the contribution rate of variance．Y1，Y2，…，Ykare k principal components calculated，and their characteristic root isλ1，λ2，…，λp，then the weighting coefficient of principal component i is：

Denoting W＝（w1，w2，…，wk）T，and establishing the composite indicator as Z＝w1Y1＋w2Y2＋…＋wkYk．

Parallel analysis is the eigenvalue method based on judging the number of principal components，and it is used to determine the number of evaluation indicators［1－2］．Firstly，a random data matrix is established，with the same size as the initial matrix，and the eigenvalues of random data matrix are extracted．Secondly，based on the comparison between eigenvalue of actual data and average eigenvalue of random data matrix，if it is greater than the average eigenvalue，then this principal component can be retained，because if the eigenvalue of original data is smaller than the average eigenvalue of the simulated random matrix，it indicates that the original eigenvalue explains few variances，and it can be ignored．

3 Principal component analysis of economic indicators［4］

According to the data provided in Table1，we use the psych package in R software to draw scree plot［3］，and the average eigenvalue（dashed line）derived by 100 random data matrices and Y＝1 horizontal line（eigenvalue greater than 1）can be shown in Fig．1．

As can be seen from Fig．1，the blue line（the lines of eigenvalues connected by the original matrix）and the red line（the average eigenvalues obtained by the parallel analysis random matrix）roughly cross under the second eigenvalue．The eigenvalues of the two principal components prior to selection are also greater than 1，and the variance contribution rate of the first two eigenvalues reaches 87．3%，which verifies the effectiveness of parallel analysis in determining the number of principal component．Using principal component analysis［5］，we extract the principal component of economic indicators，determine the weight of each principal component according to the variance contribution rate of each principal component，and establish the composite scores as comprehensive economic evaluation indicators．Using R software，the corresponding results obtained based on Table 1 are shown in Table 2 and 3．

Table 2 Correlation coefficient matrix

Table3 Eigenvalues and eigenvectors

The two principal components are expressed as follows：

Table 4 Loading matrix of principal component

It can be found that the information hidden in the indicators in the principal component loading matrix is not clear enough，so it is necessary to conduct principal component rotation．The orthogonal rotation in principal component rotation is to conduct column denoising of loading matrix，so that several limited variables can explain principal component，that is，the principal components remain irrelevant．The loading matrix treated is RC，as shown in Table 5．

Under the rotation of principal component，the cumulative variance explanation of the first two principal components after rotation does not change，and the explanation degree of each variance changes．The principal component scores are obtained by the linear combination of the original indicators，and the weight is just the load factor：

Composite score is the comprehensive evaluation function obtained by linear combination of variance contribution rate of principal components：

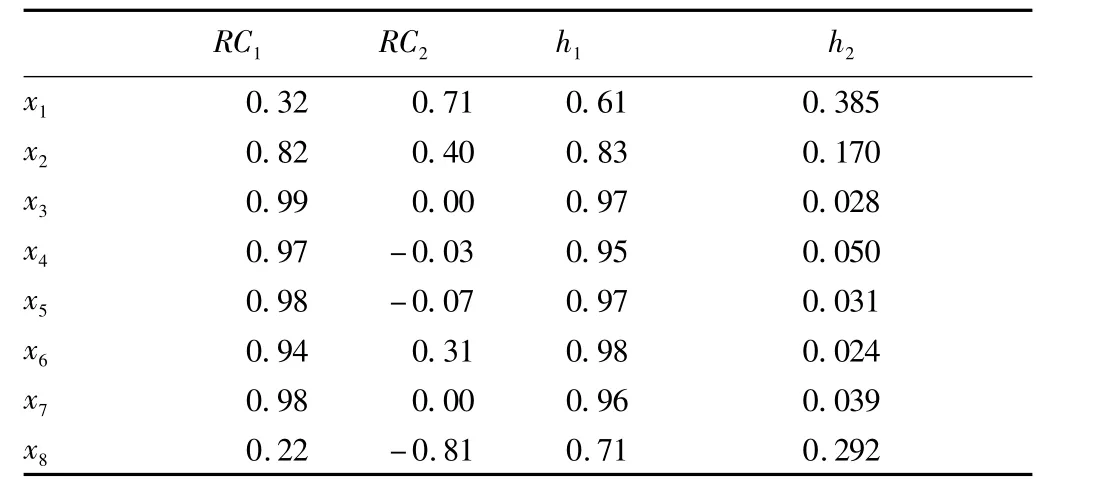
Table 5 Rotated loading matrix

Table 6 Composite score

For preliminary classification of indicators and further analysis，it is necessary to introduce clustering analysis．R clustering in clustering analysis is a method for clustering of variables．Based on R clustering，we perform the clustering on eight indicators（variables）．As can be seen from Fig．2，indicators can be divided into two categories：X1and X8as a category；X2，X3，X4，X5，X6and X7as a category．According to the loading matrix by principal component rotation，it can be found that principal component has a large load on regional GDP（X3），social fixed asset invest-ment（X4），public budget revenue（X5），public budget expenditure（X6），and total retail sales of social consumer goods（X7）．This factor mainly reflects the financial and capital flow．Principal component has a large load on land area（X1），permanent population at the end of year（X2）and import and export（X8）．This factor mainly includes hardware and import and export．The classification derived from two principal components is very similar to the classification derived from R clustering，so based on composite scores，we can evaluate the economic situation of 14 cities in Guangxi．

4 Comprehensive evaluation［5］

The cities with high scores on principal component of liquidity and financial balance（Y1）include Nanning，Liuzhou，Guilin and Fangchenggang．The absolute value of Nanning is higher than that of other cities，indicating that the regional GDP，social fixed asset investment，public budget revenue and total retail sales of social consumer goods in Nanning are much higher than in other cities，because Nanning is a provincial capital，a core city of Beibu Gulf Economic Zone，and also a financial and trading center．Similarly，Liuzhou is an industrial city and an old industrial area in Guangxi．Guilin is a tourist city and Fangchenggang is an important port city．These cities have an advantage in finance．The cities with high scores on principal component of hardware，import and export include Hechi，Baise，Fangchenggang and Chongzuo．Baise and Hechi are ranked first in terms of prefecture-level city area，and Fangchenggang is ranked first in terms of import and export．From the composite score，the top three are still Nanning，Liuzhou and Guilin．Although Hechi and Baise have high scores on the second principal component，Y1which represents economic strength still affects ranking．

［1］KONGM，BIAN R，ZHANGHC．The application of parallel analysis in exploratory factor analysis［J］．Psychological Science，2007，30（4）：924－925．（in Chinese）．

［2］MU SK，GU HG．The comparison of factor retaining methods in exploratory factor analysis［J］．Exploration of Psychology，2011，31（5），477－480．（in Chinese）．

［3］Robert I．Kabacoff．R in action：Data analysis and graphics with R［M］．Beijing：Posts＆Telecom Press，2013．

［4］JIANG Y．The economic development evaluation of the boroughs of Tianjin［J］．Application of Statistics and Management，2002，21（1）：4－9．（in Chinese）．

［5］WANG BH．Multivariate statistical analysis and modeling for R language［M］．Guangzhou：Jinan University Press，2014．（in Chinese）．