钻孔灌注桩桩侧荷载传递特性探讨
张 明,姚志龙
(湖北省地质局第八地质大队,湖北襄阳 441000)
对于桩基础的承载特性研究,国内外的学者专家已经做了大量的工作。然而在实际工程施工过程中,往往强调更多的是满足设计要求的桩承载力,而对桩承载力的要求上更多的时候表现为控制桩的沉降量。随着中国城市建设的发展,对高层建筑、桥梁建设的桩基要求也越来越高,大直径、超长灌注桩的应用也越来越广泛。本文结合湖北襄阳首信·东方墨尔本桩基础项目中的实际情况,对这一特性展开探讨。
1 桩荷载传递机理
理论研究表明桩的荷载传递机理主要包括以下两方面:地基岩土对桩的支撑作用,不同荷载下轴力沿深度的变化。地层岩土对桩的支撑由桩端阻力和桩侧摩阻力两部分组成,而且这两种阻力不是同步的[1]。竖向荷载施加于桩顶时,桩身的上部先受到压缩而发生相对于土的向下位移,于是周土在桩侧界面上产生向上的摩阻力;荷载沿桩身向下传,不断克服这种摩阻力,直至趋于稳定。而桩底的土反力作用在摩擦桩的相互作用中只占据很小的部分。
桩身轴力随着深度加深逐渐减小。在桩端处则与桩底土反力Qp平衡,同时桩端持力层土在桩底土反力Qp作用下产生压缩,使桩身下降,桩与地层土的相对位移又使摩阻力进一步发挥。随着桩顶荷载N的逐步增加,对于每级荷载,上述过程周而复始地进行,直至变形稳定为止,于是荷载传递过程结束,达到力的平衡。
如图1所示为桩身轴力的变化,随着桩顶荷载的加大,桩体产生轴力的范围也是越来越深,而且对周围土体的影响也是越来越大,影响范围越来越广,并且这种轴力的影响是不均匀的。

图1 轴力变化图Fig.1 Change maps of axial force
2 荷载传递模型
荷载传递分析法目前所使用的线弹性模型和双折线模型是常使用的用沉降侧计算摩阻的模型,但实际工程中地基条件远比这种弹性模型复杂,而指数模型和双曲线模型在实际操作过程中计算相对比较复杂,经过多重比较笔者选择使用一种三折线模型[2](图2)。
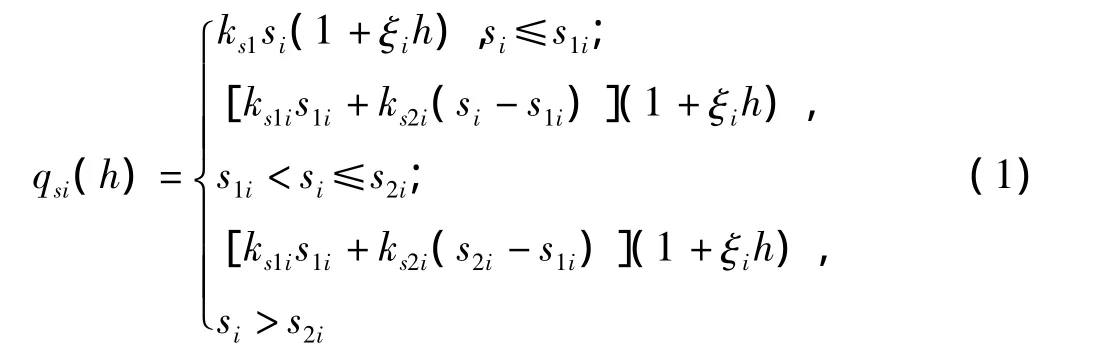
式中:qsi为第i层处桩侧摩阻力(kPa);ks1i,ks2i为桩身侧阻的刚度系数(kPa/mm);si为第i层处桩身的竖向变形量(mm);s1i,s2i为第i层处桩身土层的弹性、塑性变形临界值(mm);ξi为第i层土体的深度效应系数(m-1);h为桩身计算点离本土层中心的竖向距离(m);当桩身某点入土深度大于桩侧阻临界深度时,考虑到深度效应,取ξi=0,即不作深度修正。
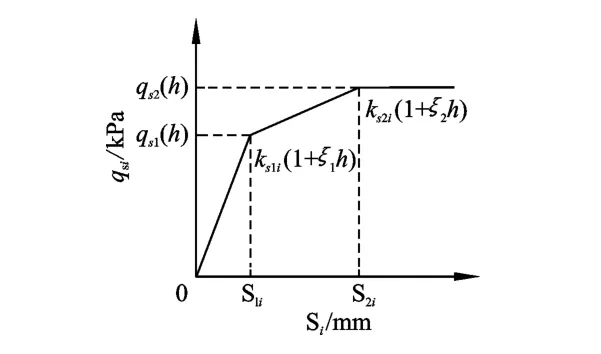
图2 侧阻三折线模型Fig.2 Model of triple line of side resistance
如图2所示,当ks2i>0,当土体达到弹性变形临界值后,开始屈服,侧阻增长变缓,开始硬化,一旦达到塑性变形之后侧阻完全发挥,将不在再增长。ks2i=0,则刚好变成双折线模型,土体屈服之后侧阻刚好完全发挥,硬化也逐渐完成。若ks2i<0,表明桩侧土体软化,土层结构被破坏,继续增压桩身将荷载传递给下面土层,桩身压缩变形最终出现沉降、桩身损坏等情况。
3 工程实例分析
该项目采用800 mm钻孔灌注桩对地基进行加固处理,单桩端入④-1卵石-6圆砾持力层,桩长在40 m左右,其地基结构如下:①杂填土(Qml),层厚4~5 m;②粉质粘土,层厚9~10 m;③粉砂,层厚1~2 m;,层厚6~8 m;④-1a粉砂层厚1~2 m;④-2圆砾,层厚7~8 m;④-3粉砂,层厚3~4 m;④-4圆砾,层厚3~4 m;④-5粉砂,层厚2~3 m;④-6圆砾为了对工程桩质量进行检验,笔者采取对三根桩进行试压,同时也提供了一个良好的检验机会。
其中在ZH-1桩试压过程中发现在桩身荷载达到4 900 kN时桩身沉降量发生明显加快的情况,但是考虑到桩身质量问题,继续加压桩体有可能产生破坏,停止静压作业。发生该情况有以下原因:①桩周围土体软化,在进行继续加压时已经到达屈服,从而直接将桩上部荷载传递到下层土体,急剧产生压缩变形,甚至是塑性变形[3]。②桩体本身存在夹泥断桩等情况,当上部荷载加压到一定值时桩体内部软弱层受到压力产生塑性位移,从而导致桩沉降急剧增加。③孔底沉渣过多,灌注桩在浇筑过程中,下部混凝土会与底部沉渣产生胶结,形成强度不高的胶结体,当上部荷载逐步传递到底层时下部强度不够的胶结体受力产生塑性变形,桩在加压过程中会产生明显沉降,如果继续加压,这种不稳定胶结体可能会逐步趋于稳定,也有可能桩体整体塑滑。
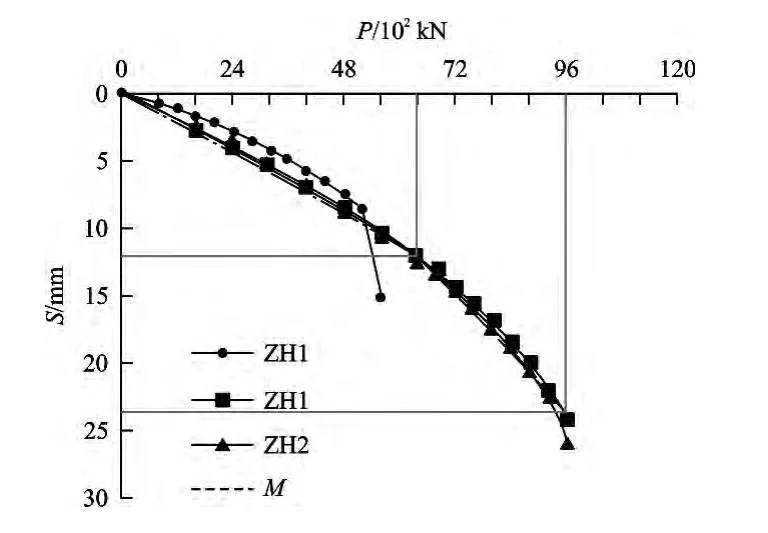
图3 静载荷试验的P-S曲线Fig.3 P-S curve of static load test
在对ZH-2和ZH-3试桩进行加压的时候,桩身产生相对速度比较均匀的沉降变形,而在荷载量达到6 000 kN左右时,沉降监测量相对之前开始有加快趋势,随着荷载进一步增加沉降迅速增加。
经过计算机模拟得出以下关于沉降与上部荷载之间的相关关系(P-S),如图3中M曲线所示。
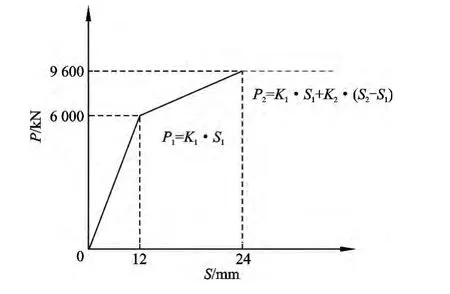
图4 P-S关系曲线模拟图Fig.4 Simulating graph of P-S relation curve
如图4所示,在整个桩体的试压过程中,笔者发现桩身的沉降与桩顶荷载关系处于一种类似上面所示的双折线模型。当上部荷载处于0~6 000 kN和6 000~9 600 kN时,桩身的沉降曲线呈两种不同斜率。
设P-S关系如下:
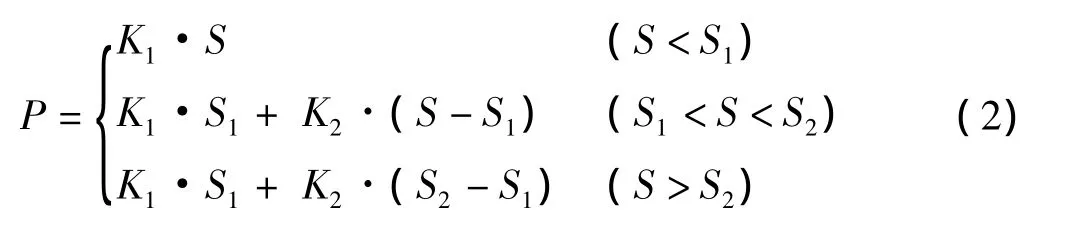
式中:P为桩体荷载量;S为桩身沉降量;S1、S2为桩身沉降速率变化时桩身沉降临界值;K1、K2为不同荷载下沉降随荷载增加产生速率,K1=500 kN/mm,K2=3 600 kN/mm。
根据式(1)和式(2)对比可知,所模拟的沉降随荷载变化的趋势吻合,从模拟和现场测试的结果来看,800 mm旋挖成孔的钻孔灌注桩,设计极限承载力在9 600 kN以内,当沉降量在0~1.2 cm时,桩的变形呈弹性形变;当沉降量在1.2~2.4 cm时,桩的变形呈塑性形变。
其中,当S>S2时的沉降量变化是根据桩身沉降规律模拟的。当桩身荷载不再增加时,随着时间的变化沉降量也会增加。
根据前面介绍的桩体沉降随荷载变化模型可知,桩身沉降变化也分为三个不同阶段,各个土层产生的沉降量都不一样。现通过数学叠加法则,对所有土层的沉降量进行叠加,即有:
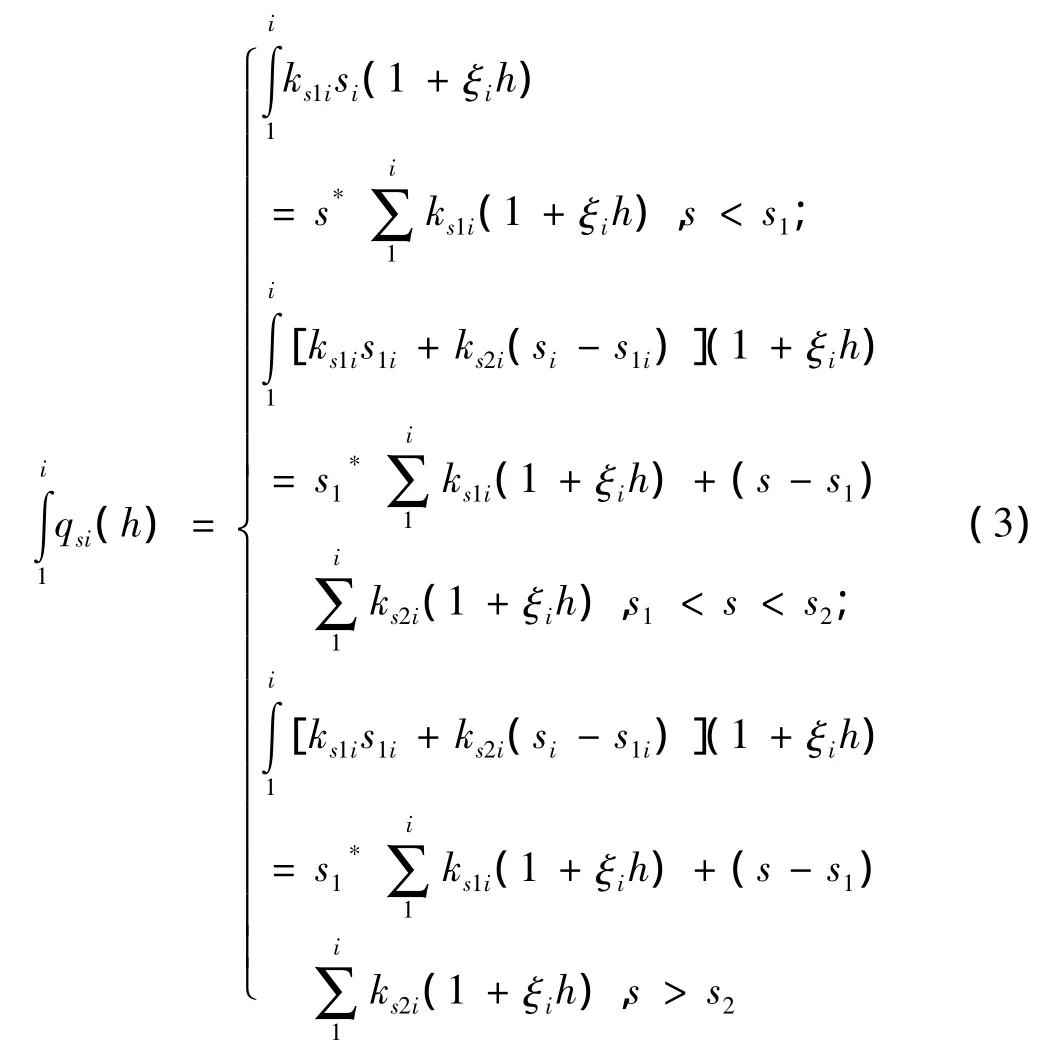
比较式(2)与式(3)可知,桩体的整体沉降与桩每一层土体中桩的沉降是有相当大的联系的。在式(3)中不妨设则有:
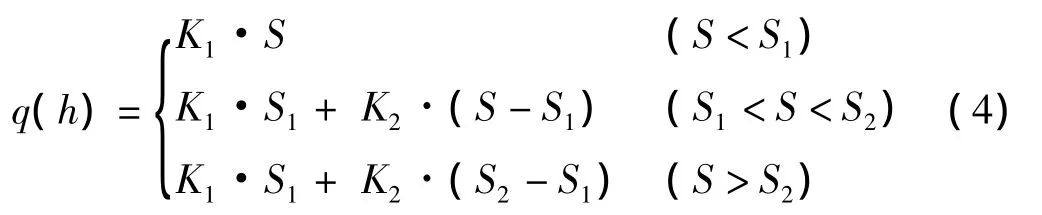
式(3)即可转换为式(4)。
式(4)是在实际沉降观察中得出的结论,而式(3)是经过理论转化得出的结论,经过比较,得出如下结论。
(1)桩基沉降速率与地层土的刚度系数成正相关。对于单层土体这种关系比较明显,但对于工程施工中所面临的多层不同地基土这种正相关则由具体的土体的相关参数综合确定。
(2)桩沉降的大小、速率与土体的弹塑性变形有直接关系[4]。桩身的沉降量与土体的压缩变形量表现极为一致,都呈现处两种不同阶段的变化。先是桩基土体达到类似于弹性形变的屈服点,然后再进行塑性形变。
(3)对比图2与图4可知,在土体弹性变形阶段,桩身沉降表现得相对较慢,而在弹性变形结束到达弹性屈服点之后桩身的沉降速度比之前快。
两者之间的转换证明,在之前采取的三折线侧阻模型能够比较好地应用到工程实际中去,这种模型能够较好地反应桩的荷载传递规律。
4 小结
本文对桩侧荷载传递特性进行了探讨,并对这一特性模型进行了验证。通过工程实例证明,该模型在实际工程操作中有一定借鉴意义,该模型一定程度上反应了灌注桩不断平衡桩侧摩阻力的过程。事实证明在地基压力的传递过程中,开始变形呈近似弹性变形,当达到近似弹性屈服极限之后,变形逐步减缓,一直到地基硬化趋于完全。这段过程中荷载是从上而下逐步向下释放的,地层土逐级压缩,直至加固完全。
[1] 黄生根,吴鹏,戴国亮.基础工程施工方法[M].武汉:中国地质大学出版社,2009.
[2] 赵明华,何俊翘.基桩竖向荷载传递模型及承载力研究[J].湖南大学学报(自然科学报),2005,32(1):37-42.
[3] 楼晓明,陈强华.工程勘察[J].1996(3):13-16.
[4] 张忠苗.基于桩顶与桩端沉降的钻孔桩受力性状研究[J].岩土工程学报,1997,19(4):88-93.

