地下连续墙“三合一结构”质量模糊综合评判研究

帅红岩

(湖北省城市地质工程院，湖北武汉 430072)

传统的地下连续墙只是作为基坑支护的一种措施，地连墙“三合一结构”是集支护挡土、防水帷幕、地下室结构外墙这三种功能合一的地下连续墙结构。地下连续墙“三合一结构”是一个多层次、多因素、多目标、多参数的系统工程，对其的评价也应是一个多层次、多指标的复杂系统工程。由于对地下连续墙“三合一结构”理论的认识不足、技术人员的专业技能差异、统计方法的局限性、指标测试方法的不可操作性，以及某些指标本身的非定量化性等原因，使得地下连续墙“三合一结构”质量评价具有层次性、模糊性、随机性［1］。从其施工工艺的单因素考量，带有极大的经验成分，不能正确反映实际情况。因此将模糊数学应用于地连墙“三合一结构”质量的综合评价中，模糊概念、模糊推理、模糊判断及模糊决策的数字化、定量化将为地连墙“三合一结构”施工质量综合评定提供理论依据［2］。本文基于模糊数学理论构建合理、科学的地下连续墙“三合一结构”质量综合评判模型，采用层次—模糊理论对地下连续墙“三合一结构”的施工质量进行综合评价。

1 模糊—层次综合评判理论

模糊—层次综合评判，即以层次分析法(AHP)［3］来确定各影响因素权重的一种模糊综合评判方法。此种方法能把复杂系统工程的决策思维与评判体系进行分层，把决策过程中定性与定量的因素、静态与动态的因素有机地结合起来。它通过把复杂的系统工程分解为不同准则层，每个准则由几个指标组成，将这些要素按照支配关系，分组形成有序的递阶层次结构，通过两两比较的方式确定层次中诸因素的相对重要性，完成判断矩阵的建立、排序计算与一致性检验等过程［4］。通过构建隶属度函数求出隶属度矩阵，将其组合形成评价指标值，利用指标值来确定评价等级，其特点是评价结果不是一个绝对的数值，而是以一个模糊集合来表示。这个评判体系适合于对多影响因素，多层次的模糊系统进行综合评价。此方法得到的最后结果比较客观、符合实际且具有说服力，与传统评定方法比较，具有明显的优越性。

2 层次结构评判模型的建立

地下连续墙“三合一结构”质量评价是一个系统工程，建立其评价指标体系是进行评价的基础工作，其科学性和合理性直接影响着评估结果的准确性。本文从支护、防水、结构三个方面建立地下连续墙“三合一结构”质量层次分析模型［5］。三合一结构质量评价体系见图1。

2．1 层次分析法确定权重向量

2．1．1 各指标判断矩阵的建立

根据地下连续墙“三合一结构”评价模糊—层次结构模型及混凝土与结构相关理论，基于层次分析法(AHP)确定影响“三合一结构”质量的各准则与每个准则下所包括指标之间的相对重要程度，建立判断矩阵表及相应判断矩阵见表1-表4。

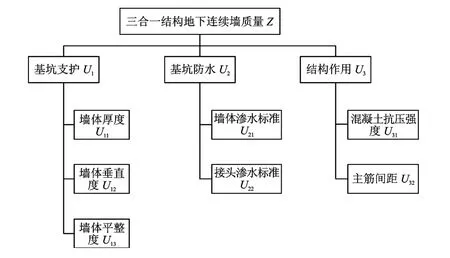
图1 三合一结构质量评价体系Fig．1 The quality evaluation system of triad structure

表1 判断矩阵表ZTable 1 Table Z of judgment matrix

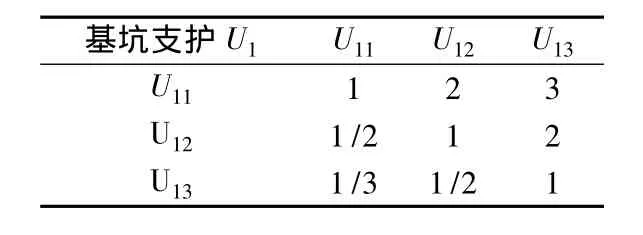
表2 判断矩阵表U1Table 2 Table U1of judgment matrix

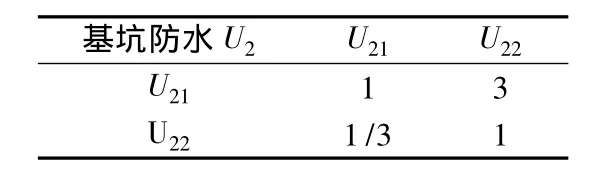
表3 判断矩阵表U2Table 1 Table U2of judgment matrix

表4 判断矩阵表U3Table 4 Table U3of judgment matrix

在每个准则层的基础上，确立其包含要素相互两两比较结果表，由以上判断矩阵表得到每一层对上一层判断矩阵，具体如下:

(1)准则层对目标层Z的判断矩阵AZ:

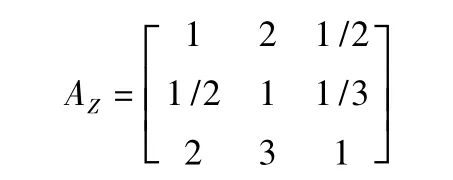
(2)指标层对准则层U1的判断矩阵AU1:

(3)指标层对准则层U2的判断矩阵AU2:

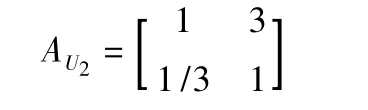
(4)指标层对准则层U3的判断矩阵AU3:

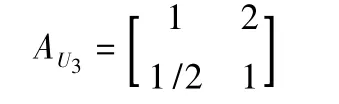
3．1．2 各指标权重的确定

(1)判断矩阵AZ的最大特征值λmax=3．009 2，对应的特征向量为:

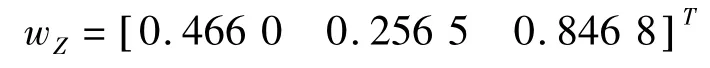
将向量wZ归一化，得到准则层对目标层Z的权重集为:

(2)判断矩阵AU1的最大特征值λmax=3．009 2，对应的特征向量为:

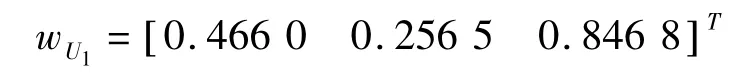
将向量wU1归一化，得到指标层对准则层U1的权重集为:

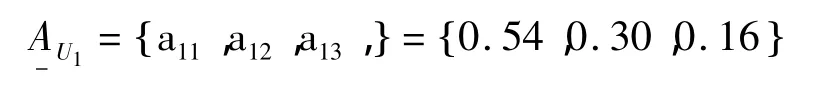
(3)判断矩阵AU2的最大特征值λmax=2，对应的特征向量为:

将向量wU2归一化，得到指标层对准则层U2的权重集为:

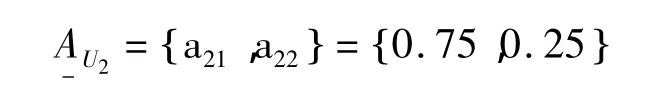
(4)判断矩阵AU3的最大特征值λmax=2，对应的特征向量为:

将向量wU3归一化，得到指标层对准则层U3的权重集为:

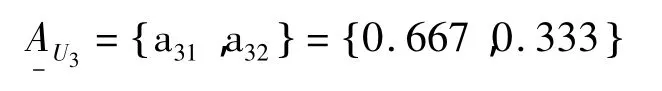
为保证每一准则下各个影响要素得到的相对权重合理，要对判断矩阵(n≥3)进行一致性检验，以观察其是否具有满意的一致性。否则，应修改判断矩阵，直到满足一致性标准为止［3］。采用Saaty推荐公式计算一致性检验指标，具体如下:

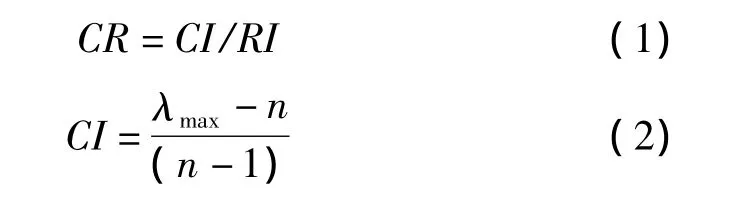
式中:CR为一致性比率;CI为一致性指标;λmax为判断矩阵最大特征值;n为判断矩阵阶数;RI为平均随机一致性指标，其值随着 n的变化而变化，具体取值见表5:

表5 RI与判断矩阵阶数n的关系［3］Table 5 Relationship between RI and order number judgment matrix

3．2 建立地下连续墙“三合一结构”质量评价集

3．2．1 地下连续墙“三合一结构“质量的评价等级

综合考虑地下连续墙“三合一结构”质量评价的要求与目的，保证质量能够满足其最基本的三项功能，建立3个等级进行评价，即m=3，构成评价集为:

V={v1，v2，v3}={优良，合格，不合格}

地下连续墙“三合一结构”各质量等级对评价因素的具体描述如下。

优良:墙体强度与规格可以很好地满足基坑支护要求，外形结构与强度可以很好地满足后期地下结构的规范与设计要求，墙体防渗效果可以很好地达到规定的后期地下结构的防水等级。“三合一结构”的三项基本功能在该等级的质量效果下完全达到设计标准。

合格:墙体强度与外形规格可以基本满足基坑支护要求，外形结构与强度可以基本满足后期地下结构的规范与设计要求，墙体防渗效果可以基本达到规定的后期地下结构的防水等级。“三合一结构“的三项基本功能在该等级的质量效果下基本达到设计标准。

不合格:墙体强度与外形规格不能满足基坑支护要求，外形结构与强度不能满足后期地下结构的规范与设计要求，墙体防渗效果不能达到规定的后期地下结构的防水等级。“三合一结构“的三项基本功能在该等级的质量效果下不能达到设计标准。

3．2．2 各项指标相对于评价集中的各个等级定义

参考湖北省《基坑工程技术规程》、《地下工程防水技术规范》以及相关规范、标准基础，对模糊—层次模型指标层中各项指标相对于评价集中的各个等级定义如表6所示。

表6 指标等级定义表［6-7］Table 6 The definition table of index grade

3．2．3 指标层各指标因素隶属度的确立

在模糊数学中，以隶属度来描述事物权重的模糊界限［8］，根据隶属的建立原则以及指标的属性原则，采用两种方式来确定指标的隶属度。当指标属于离散随机变量，其隶属度采用专家打分法;当指标属于连续型随机变量，一般采用公式法。在本模型中，墙体渗水标准、接头渗水标准属于离散型，根据其实测数据表，确定其对评价集 V中各元素的隶属度［1，9］。

本模型指标层中其余指标属于连续型随机变量，可通过公式法将实测值带入取出其隶属度，隶属函数的种类很多，这里根据各指标的随机分布特征，采用“降半梯形分布”［10］，其公式见式(3)-式(6)。

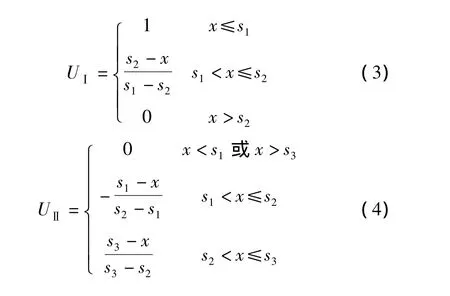
表7 某基坑指标实测值与隶属度Table 7 The measured value and membership of a foundation ditch

3．2．4 对地下连续墙“三合一结构”质量综合评判

由层次分析法得出每一个指标的权重值，组成权重向量;同时将以上7个指标对地连墙质量等级的隶属度组成单因素评价集，组成综合评判矩阵:

将权重集A视为一行模糊矩阵，则模糊综合评判关系可表示为:

对上式综合评判结果，采用最大隶属度原则，最大隶属度为0．541 5，属于评价集的优良等级，可以判断该地下连续墙“三合一结构”施工质量为优良。

4 结语

(1)根据层次分析法基本原理建立了地下连续墙“三合一结构”施工质量综合评价指标体系，确定三大准则层，7个评价指标，利用层次分析法计算各指标权重，且通过判断矩阵一致性检验确定合理的权重向量。用层次分析法和模糊数学理论建立模糊综合评判模型对工程实例进行分析，采用最大隶属度原则，最大隶属度为0．541 5，最大隶属度矩阵对应的评价等级为“优良”，因此判断该地下连续墙“三合一结构”施工质量等级为优良，与实际工程质量完全相符。

(2)地下连续墙“三合一结构”的施工质量受多种因素的影响，且众多的影响因素理论上都是随机变量，不能完全确定每一个影响因素的数学特征及其对地下连续墙“三合一结构“质量影响的相对重要性。采用层次分析法(AHP)对各影响因素分层确定其影响权重，用模糊数学理论对整个系统结构质量进行综合评分与等级划分，避免了因素过多而难于分配权重的弊端，也避免了单因素决策的片面性和人们主观认识差异所引起的决策失误，能够做出更为科学、准确、有理论依据的判断。

［1］ 赵晋乾．山岭公路隧道注浆效果评价及技术指南研究［D］．成都:成都理工大学，2006．

［2］ 王新民，赵彬，张钦礼．基于层次分析和模糊数学的采矿方法选择［J］．中南大学学报，2008，39(5):875-880．

［3］ 刘新宪，朱道立．选择与判断——AHP(层次分析法)决策［M］．上海:上海科学普及出版社，1990．

［4］ 许树伯．层次分析法原理［M］．天津:天津大学出版社，1988．

［5］ 上海市城乡建设和交通委员会．地下连续墙施工规程:DG/TJ08—2010［S］．上海:上海市城乡建设和交通委员会，2010．

［6］ 中华人民共和国住房和城乡建设部．地下工程防水技术规范:GB50108—2008［S］．北京:中国计划出版社，2011．

［7］ 湖北省住房和城乡建设厅，湖北省质量技术监督局．基坑工程技术规程:DB42/T159—2012［S］．武汉:湖北省建设工程标准定额管理总站，2012．

［8］ 张春宇，高燕希，蒋明锋，等．二级模糊综合评判在公路边坡稳定性分析中的应用［J］．公路工程，2008，33(5):109-113．

［9］ 肖盛燮，王平义，吕恩琳．模糊数学在土木与水利工程中应用［M］．北京:人民交通出版社，2004．

［10］ 秦寿康．综合评价原理与应用［M］．北京:电子工业出版社，2003．