基于模糊神经网络的RoboCup足球机器人局部路径规划方法研究

曹宇杰，邓本再，詹一佳

（长沙理工大学 电气与信息工程学院，湖南 长沙 410114）

足球机器人是目前机器人研究的热点领域之一。由于计算的复杂性、控制的实时性要求、环境的不确定因素，尤其是在包含多个障碍的复杂环境中，路径规划一直以来都是机器人运动控制中的难点[1]，国内外在机器人动态路径规划方面已经做了大量的研究工作[2-3]。路径规划就是在有障碍物的环境下找到一条由给定点到达目标点的最优路径，使机器人能够绕过障碍物，不与障碍物相碰撞[4]。常用的路径规划方法可分为传统方法，如栅格法，自由空间法和人工势场法[5]等，以及智能方法，如遗传算法，模糊逻辑和神经网络等[6-7]。针对Robocup比赛中足球机器人的碰撞情况复杂，障碍物包括本方和对方的足球机器人的情况[8]，提出了一种针对Robocup中型组比赛中处于持球状态机器人的基于模糊神经网络的局部路径规划方法。

1 路径规划算法的实现

如图1所示，机器人从给定的绝对位置PV以速度VV向给定的目标绝对位置Pr移动，而障碍物从绝对位置p(Obs)开始，以V(Obs)速度移动。不断更新机器人的直角坐标系T中机器人的位置与目标的位置，并将P(Obs)与V(Obs)转换为机器人极坐标系中的相对位置S(Obs)与相对速度U(Obs)。机器人通过模糊推断来判断其与敌方机器人之间的静态危险等级α(Obs)以及动态危险等级β(Obs)。然后机器人根据决策表中的规则来确定避障方向O(Obs)，最终导向矢量M是由矢量O与T组成的。算法的决策框图如图2所示。

图1 机器人避障模型Fig.1 Robot obstacle avoidance model

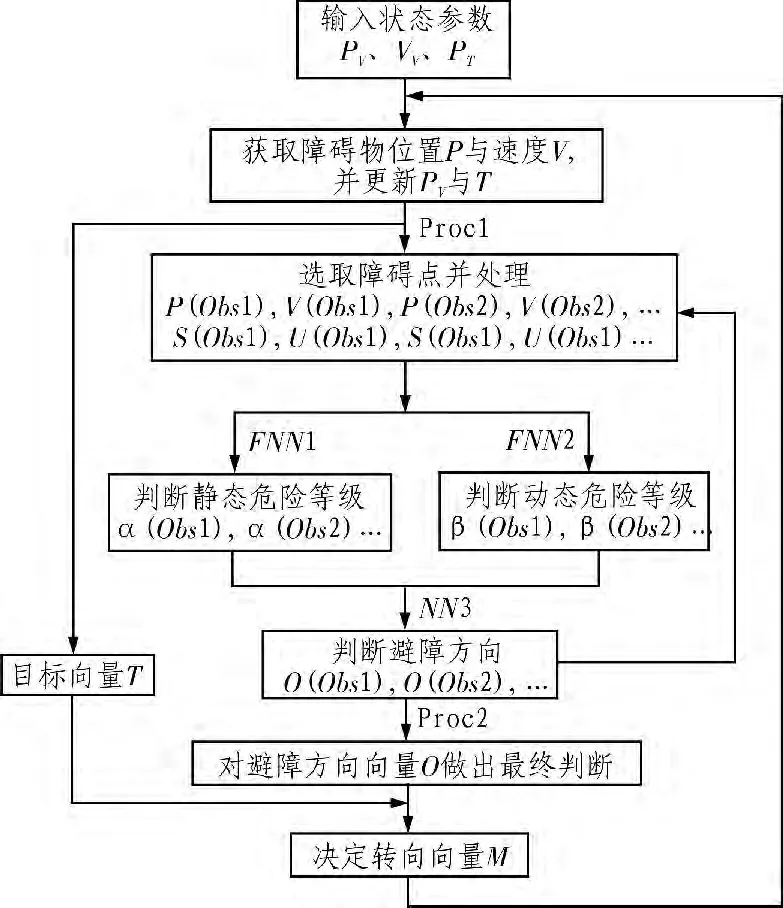
图2 程序决策框图Fig.2 The decision algorithm block diagram

1.1 判断障碍点(Proc1)

机器人通过全景摄像机获取周围环境数据，然后对图像进行识别，并将其前方范围均匀划分为11个区域。当一个敌方机器人只出现在单一区域中时，我们选择其外壳上相对本方机器人最近的点为P1,最右侧点为P2，最左侧点为P3，当某一敌方机器人出现在超过一个区域时，需要将障碍物按照区域分割，并在每个区域中都确定3个点。P1，P2，P3这3个点就构成了机器人认知中的障碍物，在进行避障时只需避免与这3个点发生碰撞。

1.2 判断静态危险等级（FNN1）

静态障碍物的危险等级取决于机器人与障碍物之间的相对位置矢量So(S(Obs)。

其中φ为机器人直角坐标系上的方向角，θS和LS分别为机器人极坐标系上的方向角与距离。将机器人正前方位置定义为0°,加值为右，减值为左。将对障碍物的探测区域限定在[-90°,+90°]内，方向角 θS的隶属度函数如图 3(a)所示，其模糊量分为 4 个等级，分别为左大（LL）,左小（LS），右小（RS），右大（RL）。

假定机器人对150 cm范围内的障碍物进行探测，距离的隶属度函数如图3(b)所示，其模糊量分为3个等级，分别为近（N），中（M）,远（F）。

静态障碍物危险等级α(Obs)的隶属度函数如图3(c)所示，其模糊量分为8个等级，分别为左侧危险性大（LDL），左侧危险性小（LDS），左侧安全性小（LSS），左侧安全性大（LSL），右侧危险性大（RDL），右侧危险性小(RDS)，右侧安全性小(RSS)，右侧安全性大(RSL)。

图3 隶属度函数Fig.3 Membership functions

FNN1采用5层结构，如图4所示，其输入矢量为XS=。

根据经验和大量的实验对的判定设定了以下模糊规则：

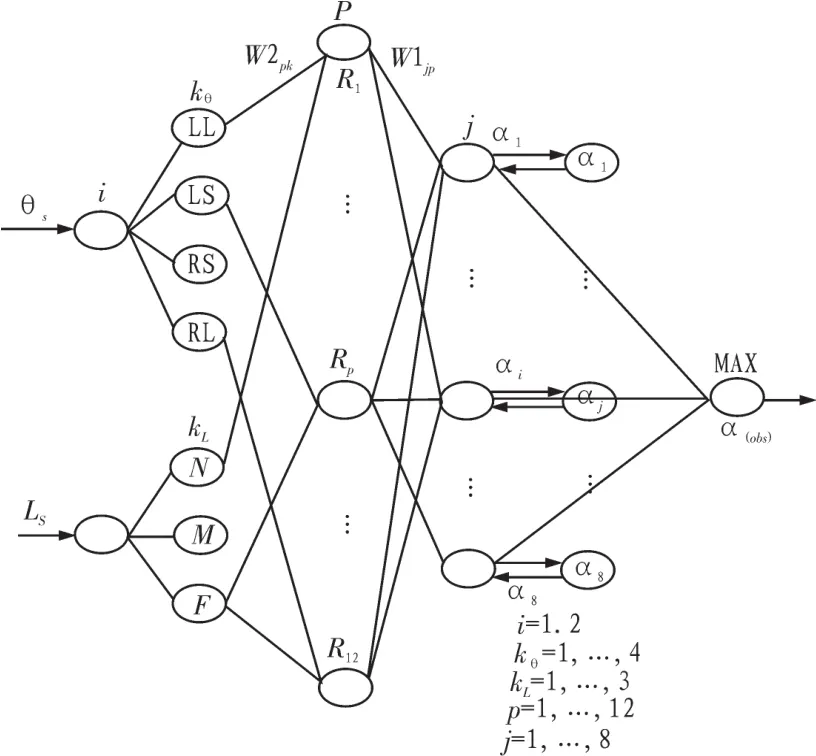
图4 FNN1结构图Fig.4 FNN1 structure diagram

第4层具有8个与输出函数对应的节点，用于执行加操作，其输出函数 f如式（7）所示，α1，α2，α3，α4，α5，α6，α7分别与LDL，LDS，LSS，LSL，RSL，RSS，RDS，RDL 对应。

第1层为输入层，有两个节点，其将对应的隶属度函数输入给下一层。

第2层为隶属度函数层，实现输入变量的模糊化，节点的个数是各个输入变量的模糊子集的和，每个节点代表一个语言变量值，其作用是计算各输入分量属于各语言变量模糊集合的隶属度函数值，节点数为7个。

第3层为模糊推理层，具有12个节点，每个节点代表一条模糊规则，它是用来匹配模糊规则的前件，计算每条规则的适用度。节点由MIN操作激活，输出函数f如式（6）所示。

第5层为输出层，通过MAX操作实现去模糊化得到α(Obs)，输出权重为1。

在FNN1的训练过程中，W1jp和W2pk的随机初始权重范围为[-1,+1]，学习效率η1=0.40，在经过K1=75次训练后能够收敛到公差Eα1=0.01。

1.3 判断动态危险等级（FNN2）

障碍物的动态危险等级β(Obs)取决于通过式（3）的R矩阵转换得到的机器人与障碍物之间的相对速度矢量UO：

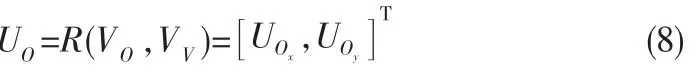
当Y轴方向与障碍物方向相同时，将变换为机器人直角坐标系上的相对速度矢量。

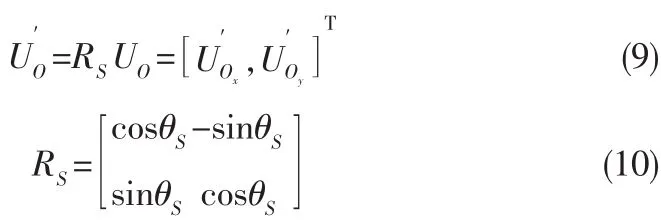
将机器人极坐标系中的速度方向和速度分别定义为ΦU和WU，将障碍物的方向定义为0°，向右加值，向左减值。

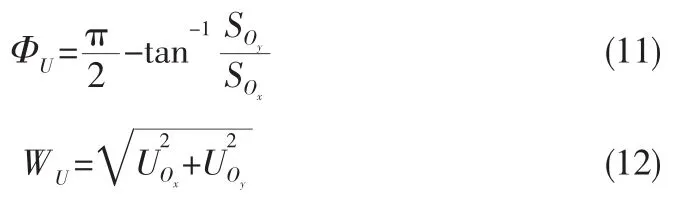
ΦU的值域为[-180°，+180°]，其隶属度函数如图 4(d)所示。ΦU的模糊量分 6个等级，分别为左大（LL），左中（LM），左小（LS），右小（RS），右中（RM），右大（RL）。的值域为，其隶属度函数如图4(e)所示。WU的模糊量分为慢（S）与快（F）2个等级。

根据经验和大量的实验对的判定设定了以下模糊规则：

FNN2的5层结构与FNN1类似,如图5所示，其中输入向量为。在FNN2的训练过程中，W1jp和W2pk的随机初始权重范围为 [-1，+1]，学习效率η2=0.30，在经过K2=55次训练后能够收敛到公差Eα2=0.01。

图5 FNN2结构图Fig.5 FNN2 structure diagram

1.4 判断避障方向（NN3）

将机器人正前方位置定义为0，对应0°，右侧依次为+1,+2,+3,+4,+5，分别对应 15°,30°,45°,60°,75°，左侧依次为-1,-2,-3,-4,-5，分别对应-15°，-30°，-45°，-60°，-75°。控制器根据决策表图6通过NN3来确定避障方向O(obs)。

图6 O(0bs)决策表Fig.6 O(0bs)decision table

将输入α(Obs)和β(Obs)分别编码为7位二进制代码α和β：

X0=[Xα1，…，Xα7，Xβ1，…，Xβ7]T

NN3的结构如图7所示。

图7 NN3结构图Fig.7 NN3 structure diagram

第1层为输入层，具有14个节点 ，用于将输入值传递到下一层。

第2层为隐藏层，具有7个节点，输出函数如式(13)所示：

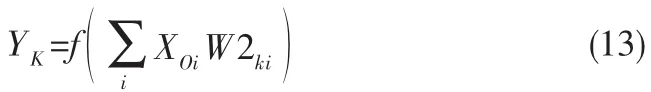
第3层为输出层，具有11个节点，输出函数如式（14）所示：

Oj的极值即 O(Obs)。

在NN3的训练过程中，W1jp和W2pk的随机初始权重范围为[-1,+1]，学习效率η3=0.40，经过K3=100次训练能够收敛到公差 Eα3=0.01。

1.5 最终决策（Proc2）

机器人的避障方向需要排除有障碍物的方向，最终机器人的避障方向取决于通过NN3获得的基于机器人直角坐标系的单位向量O。而避障动作完成后机器人的目标点T和转向向量M分别如式（15）和（16）所示：

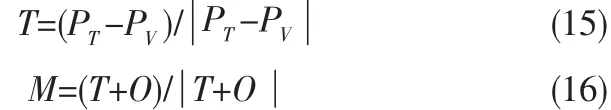
2 仿真结果

用MATLAB对本文所述的路径规划算法进行了仿真，通过MATLAB的Anfis工具和genfis()函数对实验测得的样本数据进行计算产生隶属度函数的初值。设定机器人初始坐标为（0,0），目标点坐标为(15,13),障碍物 1、2、3 的初始坐标分别为(4.5,7)、(11,6)、(9,12)，初始速度分别为（-0.3，-0.6）、(-0.7,-0.3)、(0.5,-0.5)，仿真结果如图8所示,粗实线为机器人的运动轨迹，细实线分别为障碍物1、2、3的运动轨迹，黑色圆点为目标点。

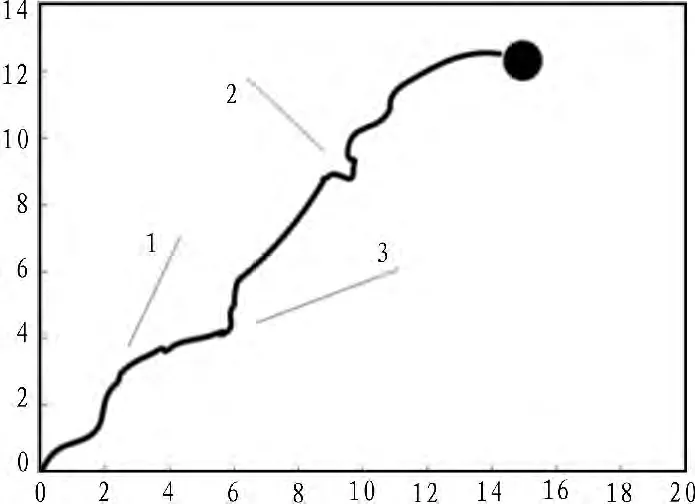
图8 仿真结果Fig.8 Emulation result

3 结论

本方法的主要特点是定义了障碍物的动态与静态危险等级，并应用模糊神经网络对其进行判断，并以此来确定避障方向。实验结果显示使用本方法在面对多个不同方向、速度的障碍物的情况下，能够根据障碍物的不同状态，做出较为准确的判断，并且具有较好的实时性，能够实现较为合理的局部路径规划。

[1]陈波，杨宜民.关于足球机器人避障控制的研究[J].机器人，2004,26(2)：111-113.

[2]Li H,Yang,Siomon X,Biletskiy Y.Neural network based path planning for a multi-robot system with moving obstacles(J).IEEE Transcation on Automation Science and Enginerring,1991,40(3):654-662.

[3]Fierro R,Lewis F L.Control of a nonholonomic mobile robot using neural networks[J].IEEE Tracsation on Neural Networks,1998,9(4):589-600.

[4]霍迎辉，张连明.一种移动机器人的路径规划算法[J].自动化技术与应用，2003,22(5)：8-10.

[5]李 实，徐旭明，叶榛.国际机器人足球比赛及其相关技术[J].机器人，2000,9(22):420-426.

[6]徐秀娜，赖汝.移动机器人路径规划技术的现状与发展[J].计算机仿真，2006,23(10):1-4.

[7]孟 蕊，苏维均，连晓峰.基于动态模糊人工势场法的移动机器人路径规划[J].计算机工程与设计，2010,31(7):1558-1561.

[8]常健，吴成东，李 斌.移动机器人避障方法综述[J].仪器仪表学报，2010,31(8)：439-442.