基于链路预测的LEO卫星稀疏自组织网络异步路由算法
戴永珊 , 姜兴龙 , 刘会杰
(1.中国科学院 上海微系统与信息技术研究所,上海 200050;2.上海微小卫星工程中心 上海 201210)
卫星星座与卫星编队飞行技术是现阶段两种主流卫星集群实现方式[1]。卫星星座系统是面向特定需求而设计的通信系统,在最初设计阶段限定了网络的规模和容量,在业务需求超过原有系统的承载能力时,需要进行网络扩容;而卫星编队飞行中以美国的F6计划[2]最为典型,以“快速响应需求、灵活采办、快速研制、快速部署、分散目标、灵活重构、适于攻防对抗”为设计目标,需要具备自发现、自动配置、故障自愈功能;此外,复杂的空间环境使卫星及星间链路存在故障风险。因此,航天任务对空间网络提出了新的技术要求——具有可快速兼容平稳扩展、自主故障发现并修复的特性,自组织网络技术正好可以解决这个技术难题。随着空间技术的发展,未来航天任务的发展正向灵活的分布式动态星座、成型空间移动平台组成的自组织空间网络[2]方向靠拢。另一方面,星座系统往往受到成本及风险的制约,在分阶段扩展部署过程中,稀疏空间网络的路由问题将是其面对的首要问题。
在Ad Hoc网络中,移动节点通过无线多跳实现相互通信,开发一种能有效找到节点间路由的动态路由算法是网络设计的关键。常用的自组织路由算法[4]主要有DSDV、WRP、AODV、DSR等,但应用于空间自组织网的路由算法研究较少。文献[2]研究了空间自组织网络的拓扑结构、消息传递机制、路由算法,其路由算法通过对空间网络中每一个节点进行特殊的多层次命名,根据节点名称的可识别性进行路由路径选择。该方法在空间系统庞大情况下,具有较高效率,而在单个卫星系统中效率极低。文献[5]提出了在LEO/MEO卫星网络中运用自组网思想,将整个网络划分成簇,将一张大网规划成子网,降低系统信令开销,该方案适用于网络节点密集,且星间结构变化不频繁的情况。
鉴于对稀疏空间网络路由算法研究的不足,以LEO卫星稀疏自组织网络为研究对象,针对缺乏持续连接(缺乏稳定的端到端路径)、高延时、网络资源有限的特点,提出一种基于链路预测的异步路由算法,并从时延最优和跳数最少两个方面对算法进行了仿真比较。
1 基于链路预测的LEO卫星稀疏自组织网络异步路由
LEO卫星稀疏自组织网络缺乏稳定连接,传统的同步路由算法通常无效,但这不表示卫星间不能传输数据。随着卫星的运动,链路在网络中不同的位置不断连接或断开。如果将单位时间内的网络看成一个静态网络,用静态的无向图描述,将多个这样的无向图按时间序列重叠,则必然存在一条或多条“基于时间推移的端到端路径”[6]。基于这种思想,通过链路预测预估卫星间的连接关系,将卫星网络通过时间-空间图描述,然后基于最少跳数、最短时延准则,运用三维的Bellman-Ford算法,得到最优路由表。
1.1 研究模型与度量标准
Walker星座具有很好的对称性,在星座系统中有广泛的应用,例如Globalstar,GPS,北斗。研究模型选择Walker倾斜轨道星座[5],由N颗卫星在P个相同倾斜卫星轨道平面组成、能够全球覆盖的卫星星座。Walker星座通常采用符号N/P/F表示,参数描述:
1)S=N/P表示每个轨道面卫星的个数,F表示 Walker星座的相位因子(F=1,2,…,P-1),F 确定了相邻轨道平面上卫星之间的偏离角度Δwf=2πF/N;
2)倾斜轨道平面的上升节点沿着赤道等间隔排列;
3)倾斜轨道平面之间具有固定的平面偏移ΔΩ=2π/P;
4)每个倾斜轨道平面内卫星以Δω=2π/S间隔均匀分布。
文中Walker星座模型为应用场景,研究LEO卫星稀疏异步自组织网络的路由算法,从而实现星上最优路径路由表生成。
根据稀疏Ad Hoc网络的结构特点[7],可归纳主要的性能度量准则如下:
1)跳数:描述了源到目的节点的组成路径的链路数量,跳数少则整体功耗低。
2)端到端时延:端到端时延指的是数据包从目的到源节点所经历的时间,包括路由等待时间和接口时延等。
3)生存时间:路由生存时间指的是路由建立开始到下一次更新所能够正常使用的时间。
4)路由容量:路由容量用来描述源到目标节点在生存时间内能够传输的最大数据量。
本算法为异步路由算法,只要前一个节点的数据成功传输到下一个节点,以前的链路不再影响后续路由,路由生存时间只与数据当前到达时间、时间窗结束时间相关,故算法选择最少跳数、最短端到端时延为最优路由路径的衡量准则。
1.2 路由算法描述
Walker星座是一个具有延迟拓扑结构[8]的LEO卫星稀疏自组织网络,不同节点对应不同卫星,节点间的连接关系代表星间链路,如图1所示(以Walker6/2/1为例)。卫星随时间不断运动,网络拓扑结构也在不断变化。传统静态图不能表示出这种变化过程,需要一系列的静态图来建立随时间变化的延迟拓扑网络结构模型。如图1所示,每一张静态图都是网络中所有节点的快照,记录当前时刻各节点间的连接关系。在T0时刻,该星座存在三条星间链路,整个网络是不连通的,不能实现从sat11至sat13的数据传送。本文描述的链路预测,是指通过STK软件实时预报的轨道信息,计算出卫星间的连通关系,得到任意时刻的网络连接图。通过约束星间的可见条件,可以模拟卫星网络的变化。
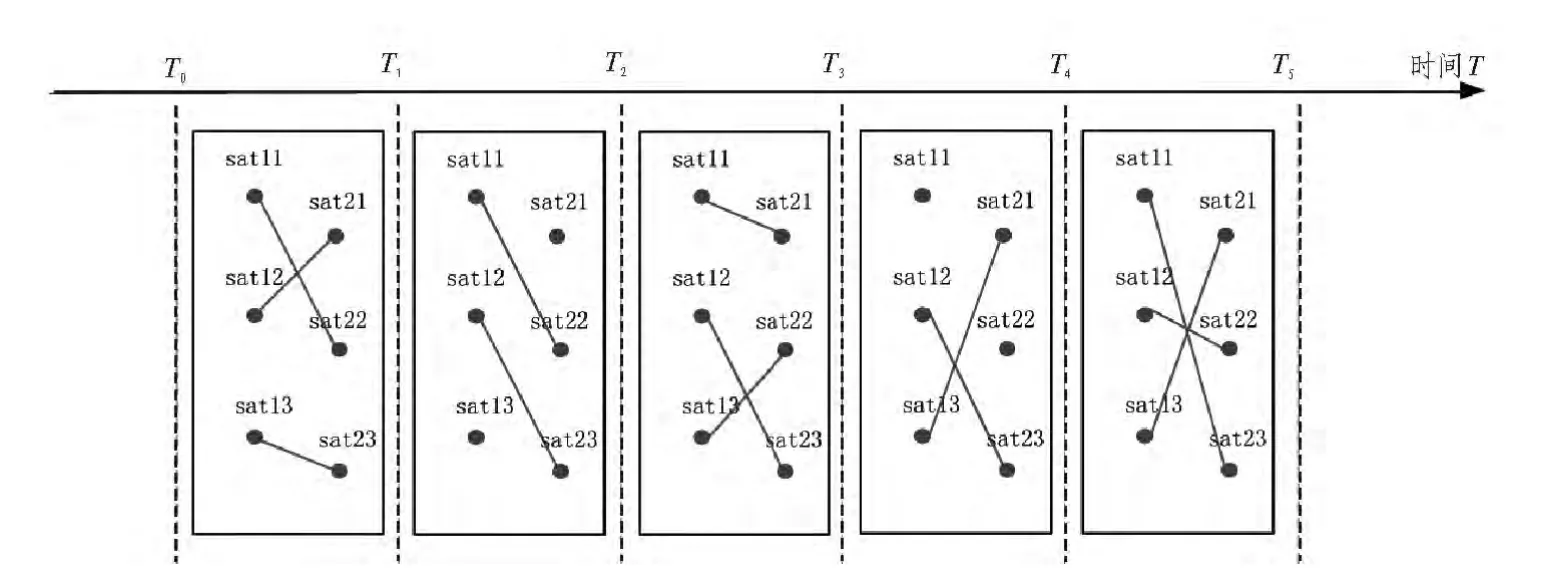
图1 卫星网络的随时间变化的连接关系Fig.1 A time-evolving topologies of a satellite network
为方便下文算法的描述,进一步分析上述模型,并转化为图论问题。将连续的时间分成离散时间序列{1,2,…,T},该星座有 6 个节点,分别为 sat11、sat12、sat13、sat21、sat22、sat23,以 S={s1,s2,…,s6}表示,而 Gt=(St,Et)表示网络在时刻 t的网络快照,其中∈Et表示节点si和节点sj在时刻t存在一条互相连通的信道,因此该网络可以表示为{Gt|t=1,2,…,T}。图2描述了在时刻t处的星座网络对应的快照示意图,这种表示法包含了空间和时间上的所有信息,与大多数现有的延迟拓扑网络路由算法适用的如图3所示的连接模型不同(在时刻t每个节点都连接着多个其余节点,有多条可选择路径,整个网络中任意两个节点互相可达,但该模型忽略了网络中的时间、顺序信息,没有反映出同一时刻链路的部分有效性),为此,本文条件下,需针对图2所示模型进行深入分析。

图2 卫星网络的网络快照示意图Fig.2 A sequence of snapshots of the satellite network at each time slot satellite network

图3 卫星网络的网络连接示意图Fig.3 The aggregated graph modelofthe
将图2的静态图转化为图4的时间-空间关系图G=(υ,ε)。由图知,该时间-空间关系图G中有T+1组节点,每组含6 个节点,其中 υ={|j=1,…,6 and t=0,…,T},是所有节点的集合,因此网络总共含6(T+1)个节点。图中所示有两种类型的链路,分别为时间链路和空间链路,组与组之间的空白部分代表的是时间的流逝,在一块空白中数据保存在本节点则向右平传,否则在该时间段内传送到下一个时间节点。因此,表示在第(t-1)秒至第t秒间,数据保存在j节点,相当于时间链路;表示在第(t-1)秒至第t秒间,数据从节点i传送到j节点,相当于空间链路。通过上述定义,时间-空间关系图中的任意一条链路都能用数学模型抽象表示,如图4所示,路径sat110sat133表示一条路由路径从节点sat11出发,在节点sat11处存储了1个单位时间间隔,在第二个单位时间间隔传送至节点sat22,在第3个单位时间间隔传送至节点sat13。

图4 卫星网络的时间-空间连接关系表Fig.4 The time-space graph of the satellite network
至此,问题转化为通过图4表示的连接关系,选择一条最优路径,由起始点至终点。即:假定链路都是可靠的,基于最少跳数、最短端到端时延原则,利用三维的Bellman-Ford算法求取最优路径。
Bellman-Ford算法基本思想是通过迭代确定最优路径。假定我们寻找一条从源节点s1到目的节点s3的最短端到端时延路径,以迭代方程表示如下:

其中,dij由每一时刻的邻接矩阵给出,若卫星i和卫星j之间存在星间链路,则设定其链路重量dij为1,否则为无穷大(Inf)。
在s1→s3最短端到端时延路径求解中,目的节点为s3,距离符号Di表示在一定限制条件下,从i节点到目的节点s3的最优路径的代价(其中i为任意中间节点),每次迭代过程中,所有节点的距离标号都是临时标号,当迭代终止时,限制条件被完全消除,因此所有节点的临时标号同时被转为永久标号,j是最优路径的中间节点。即D是第h次迭代得到的节点i的临时标号,表示经h步可到达的路径中最短径的长度。最后得到的Di=D是最终的最短路径的时延。
2 算法仿真
为了对算法的性能进行仿真验证,搭建基于STK和OPNET的仿真平台,选取典型的仿真场景进行系统建模和仿真。
2.1 仿真场景设置
仿真目的主要包括:1)验证基于链路预测的低轨卫星自组织网络异步路由算法,因此仅包含卫星交换网络,不包括地面站、终端等设备;2)分析其扩展性,比较该算法在不同规模网络结构中的整体网络性能;3)比较以不同性能度量为设计目标的系统性能,性能度量选取典型的平均时延和平均跳数。
网络规模分别选取常见的6/2/1Walker星座、12/3/1Walker星座、24/4/1Walker星座、48/8/1 Walker星座。卫星轨道选择轨道高度为1 400 km,轨道倾角为52°的圆轨道(参照Globalstar)。仿真中假设卫星天线为全向天线,限定最远通信距离为该轨道高度视距可见最大距离8 800 km,仿真周期设为2个轨道周期(轨道周期为6 600 s)。在时延统计上,假设星间链路带宽足够大,不存在拥塞,时延主要来自等待时延和传播时延。
2.2 仿真结果
根据上述设置,分别以最少跳数和最短时延为设计准则,仿真分析基于链路预测的LEO卫星稀疏自组织网络异步路由算法的可行性,得到了以平均时延、平均跳数为衡量准则的网络性能随星座规模的变化规律。
如图5所示,网络传输平均时延与Walker星座规模的变化关系,由结果分析可知:卫星的平均传输时延随着卫星规模的增加而减小。1)在网络规模较小,即LEO卫星分布很稀疏的情况下(15颗星以下),星座网络是非连通的,时延以等待时延为主(等待时延远大于传播时延),两种准则得到的平均时延普遍偏高;2)随着网络规模逐渐扩大,即LEO卫星分布相对密集情况下,以最短时延实现路由路径寻找效果更好。在卫星规模大于24颗时,星座网络是全连通的,平均时延以传播时延为主,由于系统仿真的时延统计设置最小分辨率为分钟,故该值恒为1。

图5 以最少跳数和最短时延为设计准则的平均时延Fig.5 The average cost time of the network based on minimumhops and minimum delay

图6 以最少跳数和最短时延为设计准则的平均跳数Fig.6 The average hops of the network based on minimumhops and minimum delay
如图6所示,网络传输平均跳数与Walker星座规模的变化关系,由结论分析可知:以最少时延实现最优路由路径寻找,所耗费的网络平均跳数大于以最少跳数准则,且随着网络规模的扩大,差距越明显;为实现最少跳数,网络平均最小跳数长期保持接近于1(却总是保持大于1,有一些节点不能通过一跳传输直接到达目的节点)。
综上所述,平均时延最小准则可以得到时延性能突出的路由表,但随着网络规模的扩大将带来平均路由跳数的增加,也将大大提高星间链路的传输负荷,这对稀缺的星间链路传输带宽资源提出了挑战;而平均跳数最小准则随着卫星规模的扩大,平均跳数变化相对平稳,对星间链路传输带宽要求较低,但时延性能相比平均时延最小准则大幅增加。
3 结束语
基于现有卫星集群方式,分析其组网的技术特点,考虑移动自组织网络技术,提出一种基于链路预测的稀疏LEO自组织网络异步路由算法,并通过仿真验证了算法的可行性。该算法具有扩展性、抗毁性,适用范围广的优点。
但该算法也有不足之处,算法描述模型中一个单位时间只允许一跳传输,若需要在一个单位时间间隔内进行多跳,则需要在算法中添加虚拟的路径,将多跳起始点与终点相连接,这可作为稀疏自组织网络的下一步研究问题。同时,可进一步研究考虑星间链路带宽较小并存在拥塞的情况下算法采用自适应的机制去调整路由优化的准则。
[1]董云峰,王兴龙.卫星集群概念研究[J].航天器工程,2012(4):83-88.DONG Yun-feng,WANG Xing-long.Research on conception of satellite cluster[J].Spacecraft Engineering,2012(4):83-88.
[2]吴勤.美国F6计划概况[J].国际太空,2008(5):1-5.WU Qing.The general situation of the F6 plan[J].Space International,2008(5):1-5.
[3]Chien-Chung Shen, SundaramRajagopalan, GirishBorkar.A exible routing architecture for ad hoc space networks[J].Computer Networks,2004(46):389-410.
[4]曹英烈.移动ad hoc网络路由算法研究[D].广州:华南理工大学,2006.
[5]李喆,李冬妮,王光兴.LEO/MEO卫星网络中运用自组网思想的动态路由算法[J].通信学报,2005,26(5):50-56.LI Zhe,LI Dong-ni,WANG Guang-xing.New dynamic routing algorithm based on MANET technologyin the LEO/MEO satellite network[J].Journal on Communications,2005,26(5):50-56.
[6]王欣.容迟/容断移动自组织网络路由技术研究[D].天津:天津大学,2010.
[7]Cruz-Sa'nchez H,Franck L,Beylot A L.Routing metrics for store and forward[J].The Institution of Engineering and Technology,2010,4(13):1563-1572.
[8]Huang M,Chen S,Li F,et al.Topology design in time-evolving delay-tolerant networks with unreliable links[C]//Global Communications Conference(GLOBECOM),2012IEEE.IEEE,2012:5296-5301.

