利用MATLAB软件对转向梯形进行分析验证的案例

北汽福田汽车股份有限公司诸城奥铃汽车厂 高新路

引言

转向梯形参数设计是转向系统开发中的一项重要开发指标，如果转向梯形设计不合理，则车辆转向时会导致轮胎异常磨损，甚至提前报废，对行驶安全性也有较大影响。

1 转向时理论上对转向梯形的要求

转向时理论上要求四个轮子的回转中心重合，避免轮胎的滑动。则存在下面的关系式（阿克曼原理）：

其中：K'为两主销延长线与地面交点间的距离；L为轴距；

从上式可以看出，内轮转角α1是外轮转角α0的函数。

几何分析图如图1所示。

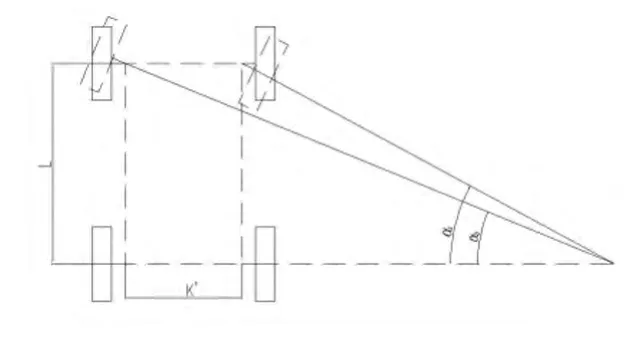
图1 几何分析图

2 对目标前桥实际转向梯形的分析

何转向梯形仅能尽量逼近），则内轮按转向梯形各杆系的运动要求转向后，内轮轮胎发生滑动或弹性变形，用于抵消内轮转角无法满足阿克曼原理导致的转角差。鉴于上面的分析，我们得出下面关系，即外轮转角α0为自变量，内轮转角α1为因变量。

转向梯形如图2所示。

现有一款本公司批量使用的前桥，目前适用于不同轴距车型。现针对此前桥进行理论分析。

定性分析可知，转向时，由于轮荷的转移，外轮轮荷增加，内轮轮荷减小，导致的结果为外轮的地面摩擦力增加，内轮的地面摩擦力减小。由于转向梯形的设计不能完全符合转向时每个车轮转角的变换（即不能完全满足阿克曼原理，设计的任

利用余弦定理等三角函数，可以推导出内轮转角α1、外轮转角α2、梯形底角γ、梯形臂长度m及两转向梯形臂球头销中心到主销的垂足点间的距离K（即图2中AB长度）的函数关系：α1=γ-arcsin

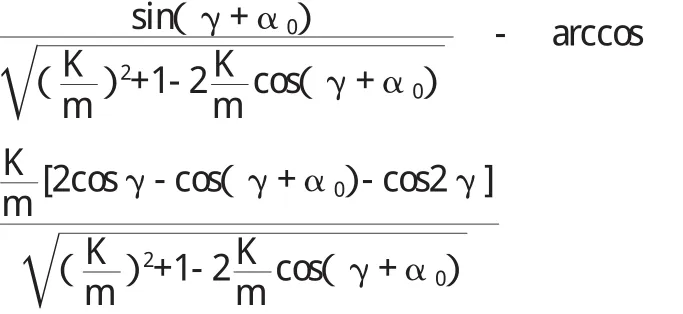
现开发车型的前桥使用轴距跨度较大，如某前桥同时安装在3800、4200、4560轴距上，对确定的前桥，转向梯形已经确定，即上式中的K、m、γ都已经确定，则很容易分析哪种轴距下最符合阿克曼原理。

对本次验证的前桥中，K为1513毫米，m为175.5毫米，γ为75度，L为三种轴距，K＇为1696毫米，将上述参数代入公式后，利用MATLAB软件，绘制得到符合阿克曼原理的曲线y和y1、y2、y3三种不同轴距的曲线，曲线如图3所示。

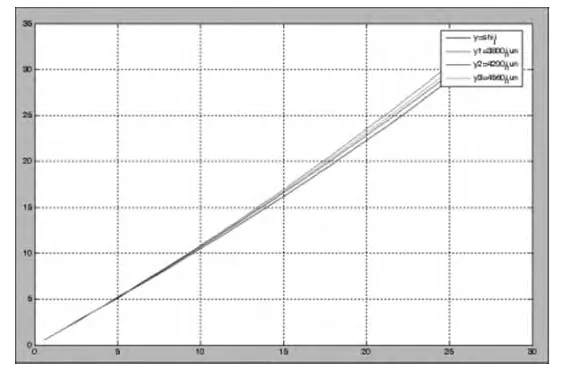
图3 曲线

图3中，横向坐标为外轮转角α0，纵向坐标为内轮转角α1。其中，y曲线为前桥实际的内外转角关系，y1曲线为3800轴距车型符合阿克曼原理的内外转角关系，y2曲线为4200轴距车型符合阿克曼原理的内外转角关系，y3曲线为4560轴距车型符合阿克曼原理的内外转角关系。由软件分析可以知道，此前桥的转向梯形最适用于4200轴距的车型。而3800轴距车型偏差较大，转向时轮胎的磨损会较其他两种轴距严重。

从上面的分析可知，设计每款车型时需对转向梯形对于每个轴距的适应性进行理性分析。如果与阿克曼原理相差较大，应重新设计转向梯形，而不应该用一种转向梯形对应于轴距跨度较大的不同车型上。

3 结论

利用MATLAB软件可以方便地对转向梯形与阿克曼原理符合性进行对比分析，合理设计转向梯形臂长度及梯形底角，可以得到足够符合工程应用的转向梯形，避免车辆使用过程中轮胎的异常磨损现象。

[1]王望予.汽车设计[M].北京：机械工业出版社,2011.