室内环境温控系统建模研究

吴 豪 ，方潜生 ，杨亚龙

（1.安徽建筑大学 电子与信息工程学院，合肥 230022；2.安徽省智能建筑重点实验室，合肥 230022）

热舒适是人对周围热环境所做的主观满意度评价[1]。影响人体热舒适的因素主要有环境因素（空气温度、平均辐射温度、相对湿度、气流速度）和个人因素（人体活动量、衣着情况），其中空气温度是最为主要的可控因素[2]。

随着我国经济发展以及人民生活水平的提高，人们对室内环境舒适性要求日益增高与能源愈发紧张的矛盾越来越严重，这就迫使寻找最佳热舒适方案。空调是改善室内环境热舒适状况不可或缺的一部分，近年来出现的地板送风、工位送风等新的空调形式，在一定程度上缓解了上述矛盾。然而空调控制系统比较复杂，运行过程中受各种不确定因素（人员流动、门窗启闭、生产工艺、设备散热等）影响，精确的数学模型很难确定，经典控制方法难以兼顾节能与舒适的要求。因此建立室内环境温度的精确数学模型并研究室内环境的温控特性具有非常重要的意义。

目前，许多学者对此做了相应的研究，文献[3]用一阶惯性环节加纯滞后环节表示室内环境温度的模型，但是每个特性参数所代表的意义及如何确定均没有明确给出；文献[4]用国内常用的估算公式确定特性参数，然而实际建筑结构多呈现不规则性和不对称性，由估算公式建立的模型精度不高；文献[5]没有考虑干扰因素的影响。本文在已有研究的基础上，结合机理分析和系统辨识2种建模方法，确定室内环境温度的数学模型，并对建立的模型进行分析研究。在原有控制系统的基础上加入模糊控制的思想，考察改进控制系统的控制效果。

1 室内环境温度数学模型的建立

通常系统数学建模的方法有2种：机理分析法和系统辨识法。本文将这2种方法结合起来，建立室内环境温度的数学模型。

首先，通过机理分析，了解空调房间温度变化机理，根据空调房间的热平衡方程，获得所需数学模型的基本形式，利用估算公式得到房间的估算模型；接着进行阶跃响应辨识，对获得的空调出风口温度和室内温度进行处理，采用最小二乘法拟合曲线，获取模型的各个参数，对建立的模型进行研究，考察本文方法所建模型的合理性。

1.1 室内环境的机理分析

本文选取安徽省智能建筑重点实验室的人体热舒适度研究室为研究对象，室内配有一台下送风方式的恒温恒湿空调。该空调房间作为被控对象，具有多容、大热容量、大时延等特性，由此建立的动态数学模型应是高阶微分方程。然而为了便于实际研究而又不失真实性，通常需要合理的简化，例如：把整个房间视为一个单容的系统，忽略房间内部气体流动，假定房间内部温度分布均匀，忽略太阳辐射的影响等。

根据上述假设并结合实际，该空调房间的示意图如图1所示。

图1 空调房间示意图Fig.1 Schematic of the air conditioning room

整个空调房间遵循能量守恒定律，即：单位时间内房间的蓄热量=（单位时间内进入室内空气的热量+单位时间内室外向室内传入的热量+单位时间内设备、照明和人体产生的散热量）—（单位时间室内向室外排出空气的热量）

列出上述关系的数学表达式，并参考文献[6]，用带有滞后的一阶惯性环节来描述该空调房间的温度对象，其传递函数为

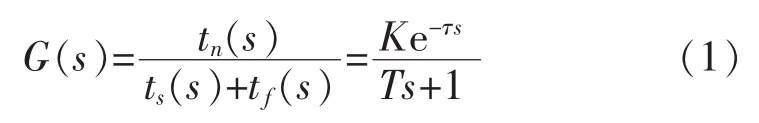
其中：tf为室内外干扰量换算成送风温度的变化量，℃；放大系数K为房间温度每降低1℃所需加入的冷量；时间常数T反应房间受到干扰后，室内温度达到新的稳定值的快慢程度；房间受到干扰后，调节参数不能立即发生变化，需要过一段时间才开始变化，这段时间成为滞后时间τ。在ts和tf共同作用下，空调房间模型结构图如图2所示。

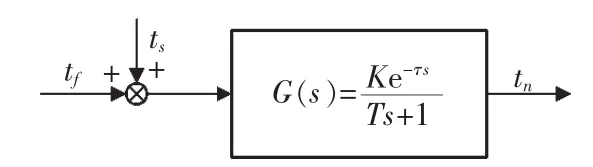
图2 空调房间模型结构图Fig.2 Structure chart of the air conditioning room model

测量实验所用房间获得如下参数：

1）房间围护结构尺寸

房间长L=8.4 m，宽W=6.1 m，净高H=2.5 m，窗户1个，窗户的长、宽、厚为1.2 m×1.2 m×0.3 m，有2面墙（6 m×2.5 m）与其它房间相邻，其余2面墙和屋顶均与室外相邻。

2）房间围护结构的材料

内、外墙均采用二四墙，屋顶设有防水层、保温层，窗户采用双层玻璃、钢质框架。

3）房间围护结构参数

计算并查阅文献[7]，确定房间维护结构参数如表1所示。

表1 房间围护结构的参数Tab.1 Room envelope parameters

4）恒温恒湿空调参数

恒温恒湿空调的送风量Gs=5200 m3/h，则空调的换气次数N=Gs/LWH=40次/h

[8]中的估算公式，通过计算得到特性参数 K=0.411、T=270 s、τ=27 s， 所以空调房间温度的估算传递函数为

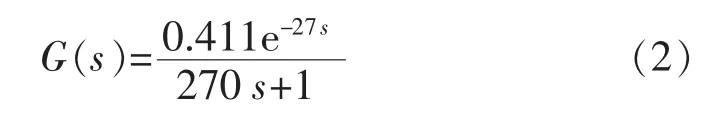
1.2 阶跃响应辨识

获取阶跃响应的基本步骤：1）保持系统工作在初始稳态一段时间；2）快速改变系统的输入量；3）记录过程系统输入输出的变化曲线直至进入新的稳态。

1.2.1 内温度数据采集平台设计

选择带有SHT11温湿度传感器的TelosB节点采集室内环境的温度数据。节点带有一个基于IEEE 802.15.4/ZigBee协议、工作在2.4 GHz频段的收发芯片CC2420。

基于ZigBee无线通信技术，搭建室内温度数据采集平台，建立了一个星型的无线网络，如图3所示。该网络中，有1个协调器节点和6个终端节点。其中，协调器节点通过USB与上位机相连，主要作用是向终端节点发送温湿度数据采集命令；然后协调器节点接收终端节点发送回来的温湿度数据，并将此数据通过串口传给上位机软件，显示并存入数据库中。

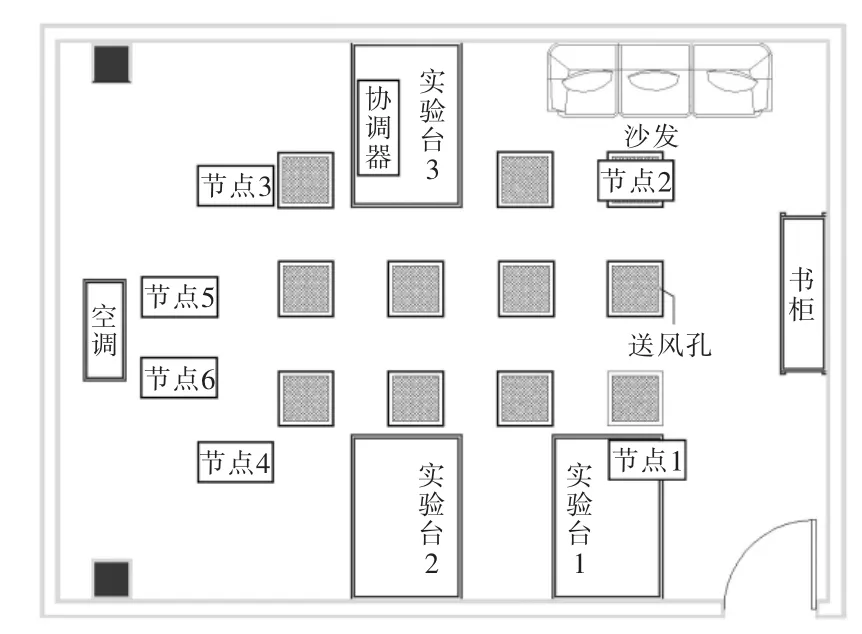
图3 温湿度测量节点分布示意图Fig.3 Distribution schematic of the temperature and humidity measure-nodes

节点 1、2、3、4 的测量高度根据 ASHRAE 62-1989规定为1.8 m以下，又因为实验研究的对象主要为坐姿，一般人坐姿高度在1.0～1.1 m，所有以离地1.1 m为监测高度，出风口处节点5、6距离出风口0.1 m，高度与出风口齐平。分别记录，空调出风口温度和空调房间的温度。

1.2.2 实验数据预处理

在曲线拟合之前必须对阶跃响应获得的实验数据进行预处理，去除有明显偏差的点以减少人为误差，提高拟合的精度。

1）节点 1、2、3、4 数据的平均值为室内温度，取节点5、6数据的平均值为空调送风口温度。

2）i时刻室内温度变化量ΔTi=Ti-T0

1.2.3 特性参数的获取

保存处理好的实验数据，并列出出风口温度的阶跃给定幅值与空调房间温度的稳态值，如表2、表3所示。

表2 出风口温度阶跃给定幅值Tab.2 Given step value of air outlet （℃）

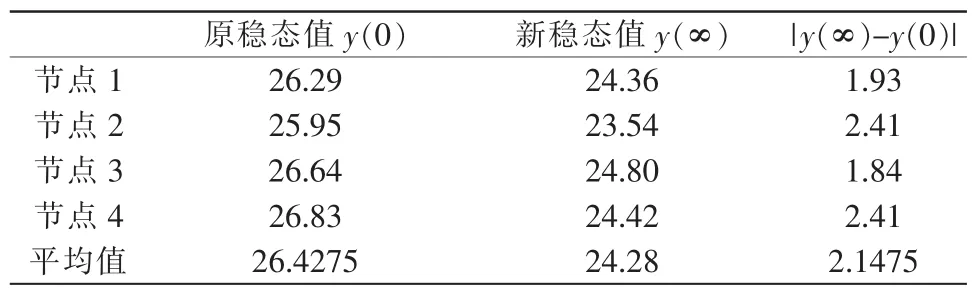
表3 空调房间温度稳态值Tab.3 Stable value of air-conditioned room temperature（℃）

放大系数K按输入输出的稳态计算：K=［y（∞）-y（0）］/r=0.505。 对式（1）进行拉氏变换，得到系统的阶跃响应：

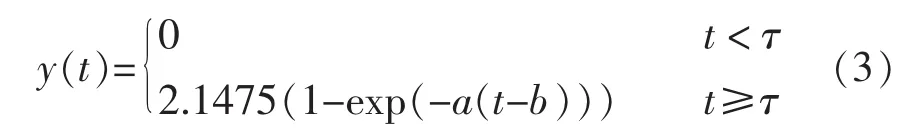
在MATLAB中利用最小二乘法进行曲线拟合，得：a=0.007777，b=28.94，sse：0.3323，rsquare：0.9799，adjrsquare：0.9796，rmse：0.0675

其中误差平方和sse越接近0拟合效果越好，判定系数rquare（主要评价标准）越接近1越好，调整自由度后的判定系数adjrsquare越接近1越好，根的均方误差rmse越接近0效果越好。由上述评价指标，可以看出拟合的效果很理想。

时间常数T=1/a、延时τ=b，根据拟合的结果，分别取T=129s，τ=29s，所以空调房间温度的传递函数：

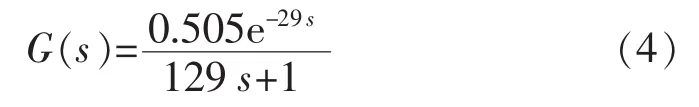
比较式（2）与式（4），可以发现本文方法与估算方法得到的模型并不相同。实际上该房间的送风方式不仅存在孔板下送风还有栅格侧送风。时间常数T与经验公式中的侧面送风和散流器送风方式得到的时间常数T较为接近，但滞后时间τ与孔板送风方式得到的较为接近。

2 系统的仿真实现

由于单独的PID控制不能在线修改参数Kp、Ki、Kd，难以满足控制要求。简单的模糊控制不具备积分环节，难以消除系统的稳态误差。因此，本文综合常规PID控制和模糊控制的优点，将2种控制结合起来构成模糊自适应PID控制。

在Simulink中建立系统的模块化仿真模型，如图4所示。其中，模块“空调房间1”采用的是估算方法建立的模型，模块“空调房间”采用的是本文方法建立的模型。

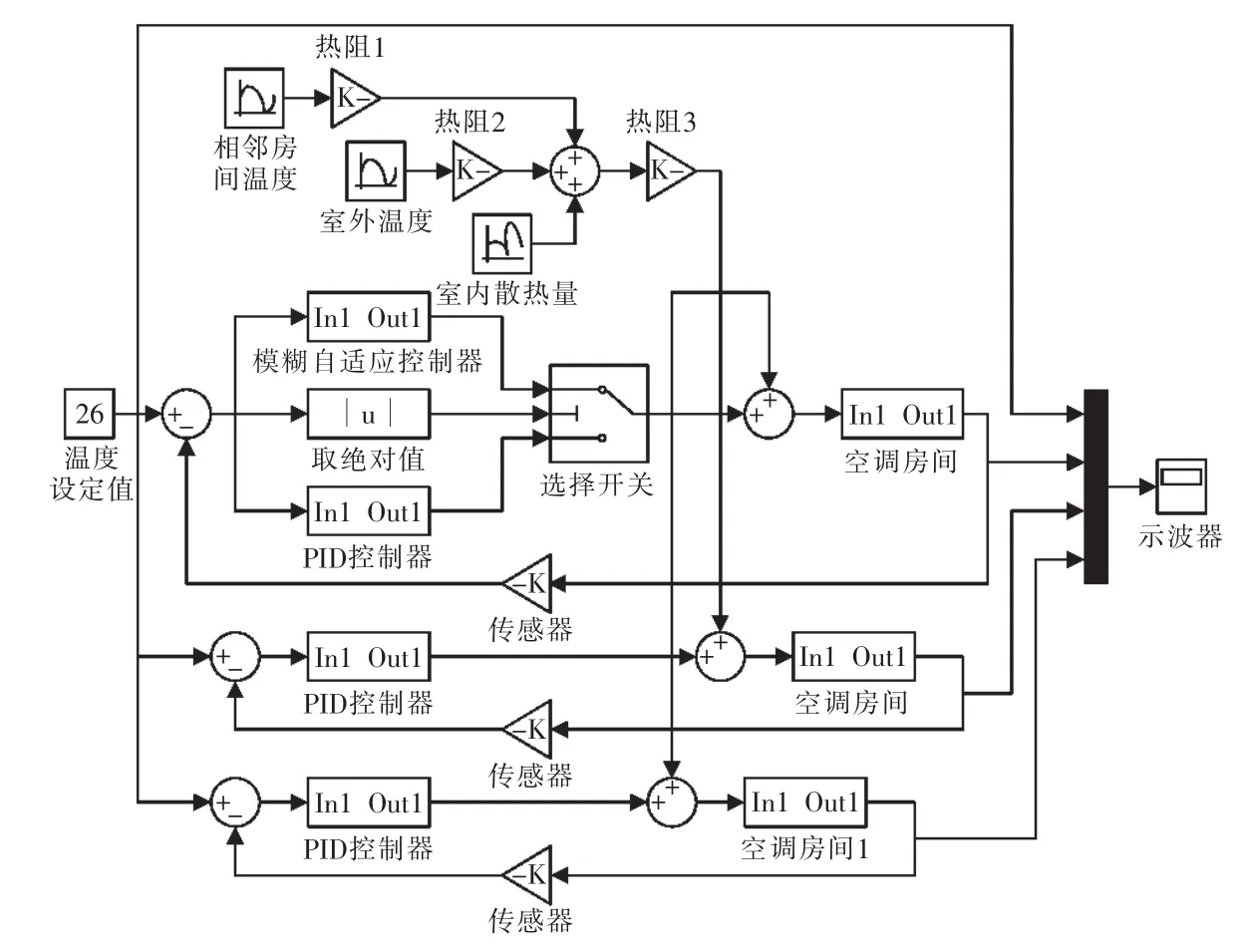
图4 温控系统仿真模型图Fig.4 Schematic of temperature control system simulation model

对2种模型都进行常规PID控制仿真，仿真时间均取2500 s，温度的设定初值为26℃，考察本文所建模型的优势。

控制器选择开关值取∣e∣=0.5℃，当∣e∣≥0.5℃时采用模糊控制；当∣e∣<0.5℃时采用常规PID控制。分别考察2种控制算法的响应时间、超调量与抗干扰能力等特性。

3 结果与分析

从图4可以看出，空调房间的输入由2部分组成：送风温度以及室内外的干扰。热阻1、热阻2、热阻3可由式（1）、（2）和表 1确定。 计算可知热阻 1，热阻2，热阻 3 分别为 0.206W/℃，0.35W/℃，0.58 W/℃。 以合肥夏季气候参数为例，相邻房间温度与室外温度，分别取正弦函数[9]。随机的室内干扰热量参照人员、照明和设备的产热指标分别为0.1 W/m2，20 W/m2，20 W/m2，实验所用房间大约50m2，计算可得Q=230W。

系统的仿真曲线如图5所示。

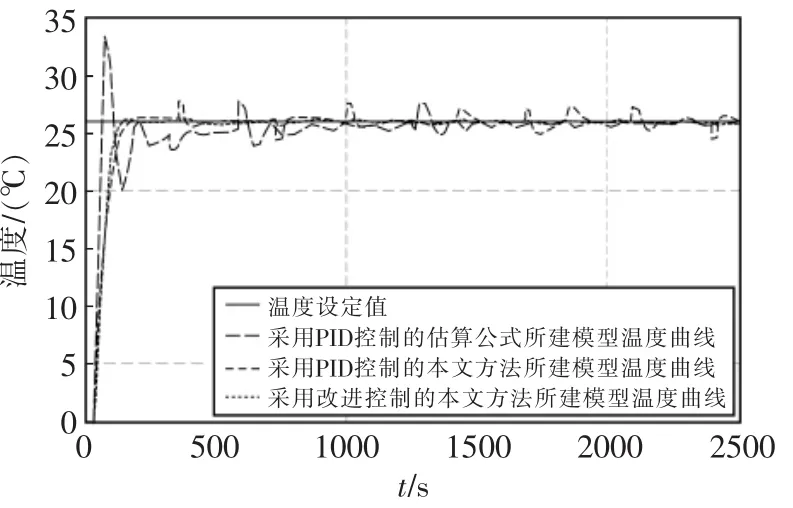
图5 系统仿真曲线Fig.5 System simulation curve

仿真结果表明，采用估算公式所建模型的PID控制系统，从0℃上升到26℃的调节时间很长，系统很难保持在稳定状态，过渡过程中存在较大的振荡，抗干扰能力很差；采用本文方法所建模型的PID控制系统，从0℃上升到26℃的过渡时间约为353 s，尽管在控制过程中仍存在着超调，但幅度较小，最大超调只有1.8℃，此外，抗干扰能力也有一定的提高；采用本文方法所建模型的改进控制系统，从0℃上升到26℃的过渡时间仅用了194 s，在较短的时间内即可达到房间温度设定值，系统的抗干扰能力很强，控制过程中，几乎没有出现超调，最大超调只有0.3℃。控制器能根据模糊规则库在线调节，在快速性、稳定性、抗干扰等方面都优于常规的PID控制。

4 结语

上述分析表明，利用机理分析熟悉空调系统的工作机理和控制过程，模型具体参数通过阶跃响应辨识获取的方法是可取的。估算方法在建模研究时有很大的局限性，该方法不适用于复杂建筑结构；本文的建模方法具有普遍适用性，建模研究时不局限于规则建筑结构，也能适应于复杂建筑结构。此外，通过辨识获取特性参数比直接用经验公式计算更准确，更能反映实际。

采用常规控制的空调系统调节时间长、超调量大、稳定性差，控制过程中存在震荡现象，这种现象不仅会缩短设备的使用寿命，同时也会消耗大量电能，造成浪费。此外，实际系统工作状况复杂，被控对象的模型往往没有仿真那样理想，这种情况下，更需要对常规控制系统进行改进。改进后的控制系统根据模糊规则库进行在线调节，实时修正参数Kp、Ki、Kd，缩短了系统的调节时间，减少了输出超调量，增强了抗干扰能力。短时间内即可使室内温度维持在设定值，避免了控制过程中大幅度震荡，提高了设备的使用寿命，节约了电能的消耗，满足了房间使用者的舒适性要求。

参考文献：

[1]ISO-7730.Moderate Thermal Environment Determination of the PMV and PPD Indices and Specification of the Condition for Thermal Comfort[S].Geneva：International Standard Organization，1984.

[2]陈翠萍.一种基于PMV指标的空调节能方法研究[D].上海：东华大学，2011.

[3]段英宏.空调房间温度预估模糊PID控制器的研究[J].系统仿真学报，2011，20（3）：620-622，626.

[4]张日楠，张九根，魏少翀.基于动态矩阵模糊PID算法的空调房间温度控制[J].计算机测量与控制，2014，22（4）：1073-1075，1086.

[5]王亚峰.空调房间温度模糊分数阶PID控制器设计及其性能分析[D].兰州：兰州理工大学，2014.

[6]G Cherem-Pereira，N Mendes.Empirical modeling of room air conditioners for building energy analysis[J].Energy and Buildings，2012，47（5）：19-26.

[7]尉迟斌，卢士勋，周祖毅.实用制冷与空调工程手册[M].北京：机械工业出版社，2011.

[8]施俊良.室温自动调节原理和应用[M].北京：中国建筑工业出版社，1983.

[9]罗妤，吴坚，徐鑫晶.合肥市平均气温动态变化的非平稳时序分析[J].安徽农业大学学报，2013，40（6）：1059-1062.