基于DELTA机器人的动力学逆解算法设计及应用
徐 恒,李梦姣,阴雷鸣
(1.四川航天职业技术学院 四川 成都 610100;2.广州数控设备有限公司 广东 广州 510165)
闭环的机构结构允许并联机器人被基座上或附近的驱动部件驱动[1]。相反,串联机器人通常由沿机构链上各个关节驱动。安装在机构链上各个关节的驱动器会对机器人本身产生巨大的负重。然而并联机器人的连杆通常没有必要承受驱动器的重量。这使得并联机器人的连杆重量比串联机器人的连杆重量要轻许多。因此并联机器人的轻重量带来了许多有潜力的价值,并联机器人的最大的缺点是它的工作空间比串联机器人要小得多[2]。
1 机构简介
DELTA机器人由静平台(上平台)、动平台(下平台)、3根主动杆、3个平行四边形从动支链组成(结构如图1所示)。基座平台的三边通过3条相同的运动链分别连接到运动平台的三条边上。每条运动链中有一个由4个球铰与杆件组成的平行四边形闭环,此闭环再与一个带转动关节的驱动臂相串联,驱动臂的一端固定在静平台上,在电动机的驱动下作一定角度的反复摆动。这3条运动链决定了运动平台的运动特性[3]。运动平台不能绕任何轴线旋转,但可以在直角坐标空间沿x,y,z 3个方向平移运动,即具有3个自由度。

图1 DELTA机器人机构图Fig.1 DELTA robot mechanism map
2 DELTA机器人运动学逆解算法
机器人运动学研究是在连杆几何约束下的机器人运动。机构学分析在不考虑引起机器人运动的力或力矩的情况下进行。机器人逆运动学问题涉及把已知的机器人输出连杆的位姿映射到能够使机器人输出连杆到达该位姿的输入关节变量的集[4]。根据DELTA机器人的机械结构,DELTA机器人运动学逆解问题是:已知DELTA机器人的动平台中心点在基坐标系中的位置,求解DELTA机器人3根主动杆和固定平台之间的角度[5]。

图2 DELTA机器人的机械结构示意图Fig.2 DELTA robot mechanical structure schematic
给定运动平台中心点P在基座坐标系中的坐标Rxyz,如图2所示,要求各驱动臂对基座平台的张角。定义坐标Ruvw系其 W 轴和Z轴重合,U 轴指向点 Ai(i=1,2,3)。由基座坐标系Rxyz到坐标系Ruvw的坐标变换矩阵为
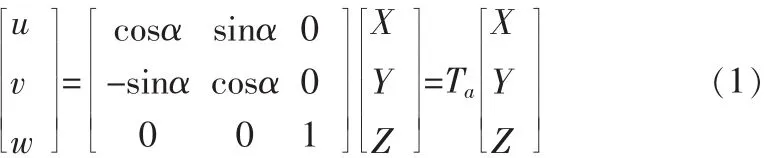
则点P,Ai及Ci在坐标系Ruvw中的坐标为:
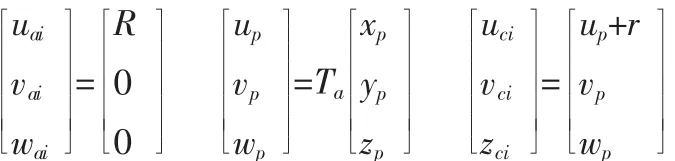
点Bi的运动轨迹应当在以Ci为中心,半径为从动杆m的球面上,于是得:
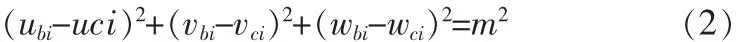
点Bi的运动轨迹也应当在以Ai为圆心,半径为n,且位于u-w平面内的一个圆上,则有:
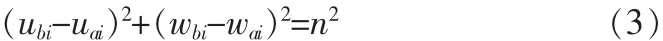
连立求解方程,一般可得到园和球面的两个交点,其坐标为
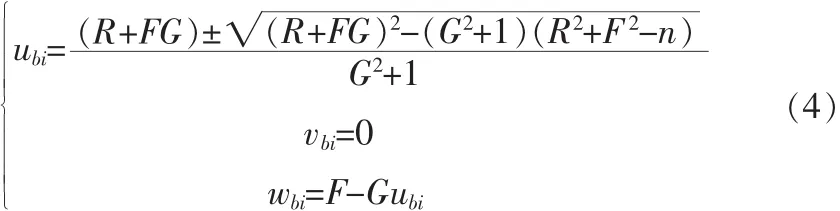
3 工作空间分析
工作空间运用空间几何来描述机器人的性能。机器人正常运行时,机器人末端执行器的坐标系原点能够到达的所有点的集合构成了机器人的工作空间。机器人的工作空间包括两个基本问题的求解:机器人的工作空间分析和机器人工作空间的综合[6]。本文运用解析几何的方法计算DELTA机器人的工作空间:

图3 DELTA机器人坐标图Fig.3 DELTA robot plot

将上式化简为:aisinθi+bicosθi-ki=0
因此可以得到不等式:
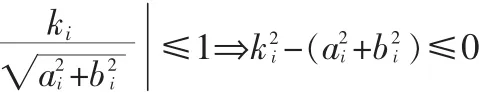
即为:

上面这个不等式即表示一个空间范围,该空间边界为Qi(x,y,z)=0 (i=1,2,3)。 以上的等式都是建立在固定坐标系R(,,中,在此定义一个新的旋转坐标系 T(,),其中:
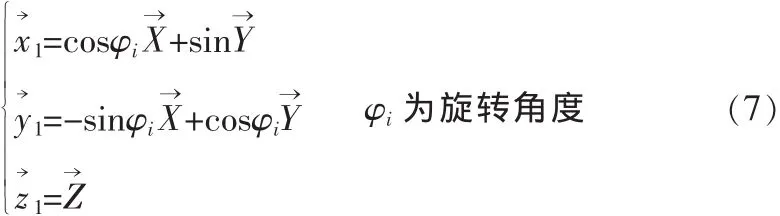
所移动平台中点O′在旋转坐标系T中的位置矢量为:
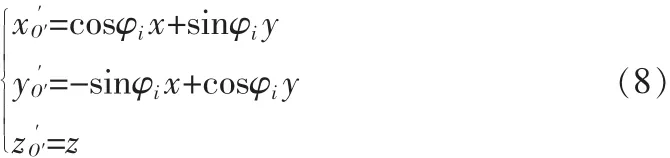
将空间边界 Qi(x,y,z)=0 经过简化后在旋转坐标系中表达式为:
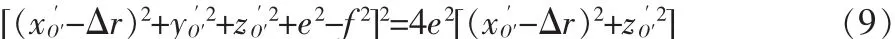
上面的形式与圆环的标准方程一致,其中:
圆环中心为(Δr,0)T=(Δr cosφi,Δr cosφi,0)R
4 结束语
DELTA机构具有并联机器人机构的诸多优点,在不少领域有潜在的用途。研究其在大负载情况下的应用,是一个重要的方面。本文提出了一种DELTA型并联机器人运动学逆解的几何解法,充分利用DELTA机构的特殊几何特性及运动约束条件,求解过程简单、直观,推导过程的每一步都有明确的几何意义。
[1]马香峰.工业机器人的操作机设计[M].北京:冶金工业出版社,1996:99-106.MA Xiang-feng.Industrial robot manipulator design[M].Beijing:Metallurgical Industry Press,1996:99-106.
[2]George P.Moustris,Spyros G.Tzafestas.Switching fuzzy tracking control for mobile robots under curvature constraints[J].Control Engineering Practice,2011(9):45-53.
[3]黄真.并联机器人机构学基础理论的研究[J].机器人技术与应用,2005(6):11-14.HUANG Zhen.Study of the basic theory of?parallel robotic mechanism[J].Robot Technology and Application,2005(6):11-14.
[4]YANG Chi-fu,ZHENG Shu-tao,LAN Xin-jie,et al.Adaptive robust control for spatial hydraulic parallel industrial robot[J].Procedia Engineering,2011(15):331-335.
[5]Fernando Castanos,Leonid Fridman.Dynamic switching surfaces for output sliding mode control:An H approach[J].Automatica Volume 47,2011(9):1957-1961.
[6]刘辛军,汪劲松.一种空间3自由度并联机器人的工作空间和转动能力分析[J].自然科学进展,2005(2):100-103.LIU Xin-jun,WANG Jin-song.A space workspace and 3-DOF parallel robot rotation capacity analysis[J].Progress in Natural Science,2005(2):100-103.

