无人车的巡航控制系统的设计与仿真
刘智平,薛晋强
(西安工业大学 计算机学院,陕西 西安 710021)
无人车是在有人车的基础上的继承和发展,主要借助了自动控制技术、计算机技术、数学、信息处理技术上的研究成果。随着电子技术、传感器技术、计算机技术、自动控制技术的飞速发展,汽车行业已在如下领域取得了显著的进展:辅助驾驶系统;主动稳定控制系统;车辆的驱动性能;交通管理;燃料的经济性。但是,即使有人驾驶的小汽车,自适应巡航控制系统的拥有率仍低于64%。众所周知,无人车由于可以完成危险环境下的作业、狭小且不适合人生存的环境下的作业,而且这一优势正在不断拓展到许多新型领域。因此,智能化的无人车早已被美国列为高技术研究项目之一,现在为世人所熟知的无人车有美国的火星探测车、中国的月球探测车、欧盟的彗星着陆器等。但有一个不争的事实,那就是无人车的技术基本上来自有人车的技术。
针对国内汽车所面临的竞争形势,文献[6]从汽车的动力总成系统、动力安全系统和新能源汽车中的关键技术等方面展开了详细的论述,指出了汽车控制系统中的共性问题。文献[7]给出了一款无人操纵的电瓶车的路径跟踪控制器的软硬件设计,文献[8]结合汽车模型的非线性、路面参数和行驶状态参数随时间的变化特性之间的耦合特性,指出了这些参数估计的困难所在。文献[9]给出了汽车巡航控制的分层设计思路,此思路可推广到其它车辆的控制系统的设计上。文献[10]给出了月面上行驶的无人车的牵引控制策略,可供复杂地面路况行驶的无人车的控制系统的设计借鉴。随着任务难度的增加,单一无人车完成不了的任务需要多个无人车协调完成,这就是无人车的编队控制,无人车的编队控制朝着自主化、网络化的方向发展。
综上所述,无人车的设计与制造、动力学建模、控制系统的设计、路径规划、避障等方面都存在着亟待解决的技术问题。本文是在前人的研究工作的基础上,针对现在电力驱动的无人车的巡航控制问题展开研究,考虑了车辆之间相对的安全距离的限制、传感器信息的延迟、作动器的时间延迟对巡航性能的影响,针对仿真结果中出现的现象,提出了后续研究的新内容。
1 无人车的动力学模型和运动学模型

图1 汽车转弯时的运动学关系图Fig.1 Kinematics diagram of vehicle during turning
我们考虑的是两个后轮驱动的四轮车,其左转弯过程示意在图1中。关于建立车体模型所需要的坐标系的定义,见文献[1]。图1所示的转弯过程只是用于推动车辆的动力学模型和运动学模型,发动机的模型、悬挂系统的模型、轮胎的模型在此略去。在后续的控制律设计与仿真中,以简化的形式给出轮胎的相关力学参数、发动机的扭矩和速度之间的函数关系。图1中相应的符号的含义解释如下。R为车体质心处的转弯半径,RRi,i=L,R表示左后轮和右后轮的转弯半径,RRi,i=L,R表示左前轮和右前轮的转弯半径。bF、bR为前轮距和后轮距,ψ是车体的航向角,β是车体的侧滑角,lF、lR分别表示车体的质心距离前轮轴和后轮轴的长度,δW是轮子的调整角度,VG是车体质心处的速度,αFi,i=L,R 是前轮的侧滑角,αRi,i=L,R 是后轮的侧滑角,UWFi,i=L,R 表示前轮的速度,UWRi,i=L,R 表示后轮的速度。
为了模型推导和简化之便,做如下假设:
1)车体和轮子的侧滑角较小;
2)前轮的调整角相等,后轮的调整角相等;
3)车体的转弯只持续较短的时间;
4)前轮和后轮与地面的摩擦系数是相等的;
5)汽车的速度处于一个相对稳定的范围内。
在上述假设的基础上,基于图1推导得出的平面上运动的汽车的动力学模型和运动学模型可以简化。
简化后车辆的运动学模型为

汽油发动机的驱动力输出和车体速度之间的关系为:

其中,Tm是发动机的最大输出扭矩,ωm是发动机的最大转速,αn是和档位、车轮半径有关的参数,u是油门量,λ是功率参数。
车体简化后的动力学模型为:

方程(3)中的cR、cF为后轮轮胎和前轮轮胎的侧滑刚度系数,lR和lF分别是车体的质心与后轴和前轴的距离,δw是前轮的调整角,JZ是车体的航向转动惯量,其余变量的含义后续解释。由(1)~(3)描述的汽车模型,针对水平路面上的巡航、跟踪等问题的研究是足够了。有时会根据需要再次进行简化,以便于控制系统的结构和参数的初步筛选。
2 无人车的巡航控制器的设计
针对简化的车体模型,我们考虑了相对距离和相对速度的限制。具体的巡航控制逻辑简述如下,在巡航控制过程中,首先利用车载传感器车辆车体和前方车辆的相对距离,如果该相对距离大于预定的最小安全距离,则立即刹车。如果相对距离介于最小预定值和最大预定值之间,车体的指令速度按照巡航逻辑计算得出。如果该相对距离大于最大的预定值,则车体可以自身的最大速度行驶。在巡航速度逻辑里,如果车体的速度低于前方车辆的速度,则可以较高的速度行驶,若车体的速度高于前方车辆的速度,则需以前方车辆的速度行驶。
具体的巡航逻辑函数如下。

其中,VL是前方车辆的速度,Vmax是无人车的最大速度,V是无人车的即时速度,hst为最小的安全距离,hgo为最大的安全距离。
为了简化仿真模型,除了采用方程(1)~(3)外,先采用一个更为简单的模型[2],这个模型为点质量模型完全忽略了车体的惯性矩,如方程(5)所示。

其中,θ是路面的倾角,u是油门量,αn是传动系统的系数,T(v)是扭矩,Cr是滚动磨擦系数,ρ是空气的密度,Cd是气动阻力系数,A是车体的迎风面积。由于发动机的输出扭矩和发动机的转速之间是非线性关系,而发动机的转速和车速是线性惯性,不考虑瞬态响应过程,拟合出来的扭矩和车速之间的关系为

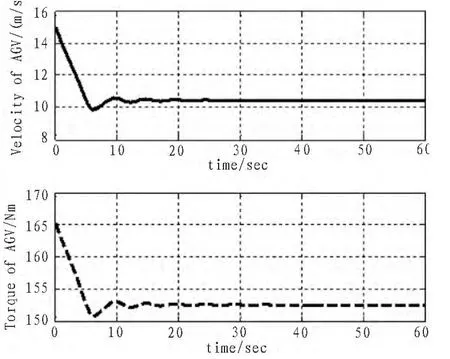
由于式(6)中的a2< 为了更准确地仿真巡航控制的效果,假设车体的速度恒定,车辆沿直线轨迹行驶,则控制量只有油门量一个物理量。基于式(3)的简化模型为 针对式(7)所描述的线性系统,即可应用线性反馈控制方法实现镇定和跟踪。具体的控制律的形式为 虽然从理论上说,控制律的设计不存在问题。但从现实的角度看,基于方程(6)和 (7)的闭环系统的性能显而易见地和车辆的速度、轮胎的参数、车体的参数有关,同时和道路的坡度有关。因此,即使假设的极点配置位置是固定的,由于道路参数的变化、车体的速度的变化、轮胎参数的变化,也会导致反馈系数的改变。 至于传感器的延迟、作动器的延迟带来的影响的理论分析在此略去,在仿真部分,只给出时间延迟的影响结果。 本文仿真时,选取的汽车的参数如下。 选取的最大安全距离为35 m,最小安全距离为5 m,最大的跟踪速度为35 m/s。如果不考虑传感器的时延、作动器的时延,选择如方程(5)所示的简化模型,选择如方程(4)所示的巡航逻辑函数,则仿真结果如图2~4所示。 由仿真结果可知,巡航控制系统的效果是理想的。如果考虑了传感器的时延、作动器的时延,可以预计得到,此时的系统响应会出现滞后,性能会下降。具体的仿真结果见图4~5。在图4和图5中,时间延迟设定为0.5 s,滞后的效果已经比较明显。如果时间延迟较大,而且每个子系统的时延还不一致的话,可以肯定地说,仿真的效果会更加恶化。 需要说明的是,1)上述仿真结果是在车体的爬坡角度小于5度、车体的行驶速度不大于35 m/s的条件范围内给出的其中的一组,控制律的设计是基于线性化后的系统模型得出的。2)从仿真结果看,坡度的出现对线性反馈控制律的设计是有影响的,但这个影响通过控制律适当的修正是可以改进的,这和文献[1-2]中提到的结论是一致的。 图2 发动机的输出力矩和车体的速度Fig.2 Torque and velocity 图3 油门量和输出力Fig.3 Throttle and driving force 图4 具有时延时的速度和扭矩Fig.4 Velocity and torque with time delay 时延对系统的性能的影响、对控制系统设计的影响是一个由来已久却没有很好地解决的问题,时延不仅降低了系统的整体性能,有时甚至导致闭环系统失稳。 图5 具有时延时的油门量和驱动力Fig.5 Throttle and driving force with time delay 文中针对无人车辆的巡航控制问题进行了研究,提出了简化的数学模型,考虑了相对安全距离、车速、时间延迟等因素的影响。基于线性化的车辆运动模型,给出了控制律的设计及其数学仿真验证,同时考虑了时间延迟的影响。仿真结果表明,基于线性化的模型和线性反馈控制律可以实现车辆的巡航控制,只是需要满足道路的坡度、时间延迟满足一定的要求。后续的研究宜将重点集中在非线性模型和非线性控制律的设计与仿真、时间延迟对闭环系统性能影响的理论分析方面。 [1]Rajamani R.Vehicle dynamics and control[M].Springer,2012. [2]Astrom K J,Murray R M.Feedback Systems-An introduction for scientists and engineers[M].Princeton University Press,2008. [3]Weyer J,Fink R D,Adelt F.Human-machine-cooperation in small cars[J].Safety Science,2015(72):199-208. [4]Marino R,Scalzi S,Netto M.Integrated driver and active steering control for vision-based lane keeping[J].European Jpurnal of Control,2012(5):473-484. [5]Andrzejewski R,Awaejcewicz J.Nonlinear dynamics of a wheeled vehicle[M].Springer,2005. [6]陈虹,宫洵,胡云峰,等.汽车控制的研究现状与展望[J].自动化学报,2013,39(4):322-346.CHEN Hong,GONG Xun,HU Yun-feng,et al.Automotive control:the state of the art and perspective[J].Acta Automatica Sinica,2013,39(4):322-346. [7]张立广,谭宝成,马天力.无人机驾驶车辆路径跟踪控制器的设计与实现[J].西安工业大学学报,2013,33(8):680-684.ZHANG Li-guang,TAN Bao-cheng,MA Tian-li.Path Tracking’s design and research of unmanned vehicle[J].Journal of Xi’an Technological University,2013,33(8):680-684. [8]郭洪艳,陈虹,赵海艳,等.汽车行驶状态参数估计研究进展与展望[J].控制理论与应用,2013,30(6):661-672.GUO Hong-yan,CHEN Hong,ZHAO Hai-yan,et al.State and parameter estimation for running vehicle:recent developments and perspective[J].Control Theory&Application,2013,30(6):661-672. [9]裴晓飞,刘昭度,马国成,等.一种汽车巡航控制的分层控制算法[J].北京理工大学学报,2012,32(5):479-483.PEI Xiao-fei,LIU Guo-du,MA Guo-cheng,et al.A hierarchical control algorithm of automobile cruise system[J].Transactionsof Beiing Instituteof Technology,2012,32(5):479-483. [10]彭兴文,崔平远,居鹤华.基于动力学模型的月球车的闭环牵引控制[J].宇航学报,2009,30(2):560-565.PENG Xing-wen,CUI Ping-yuan,JU He-hua.Closed-loop traction control of lunar rover based on dynamic model[J].Journal of Astronautics,2009,30(2):560-565.

3 仿真与分析



4 结 论


