基于GA-SVM 的带钢表面缺陷模式识别
陈 功, 苗 瑞, 张 洁
(上海交通大学 机械与动力工程学院, 上海 200240)
模式识别即模式分类,旨在研究在原始样本数据中寻找一种区分不同种类对象的客观规律,依据规律构建一个分类器,实现对新的样本不同种类对象的自动归类。 随着社会的高速发展,我国对带钢的需求量不断增大,然而由于加工环境,加工工艺,设备等原因,带钢表面在生产工程中容易出现诸如擦伤,辊印,锈斑,麻点等各种缺陷[1]。 对上述不同种类的缺陷进行模式识别,有助于分析各类缺陷成因,改进生产参数,所以是十分必要的。
对于带钢缺陷的模式识别主要包括图像采集, 特征提取,图像分类识别几个步骤。 其中图像分类识别作为其中一个关键技术,长久以来没得到良好的解决。 图像分类识别是对图像信息,如灰度,纹理等特征参数建立机器规则,使得机器可以自动快速地对缺陷进行归类。 图像识别的常用方法包括统计模式识别方法、人工神经网络以及基于核机器学习的方法等。 其中以支持向量机(SVM)作为模式识别的工具被广泛采用,SVM 对于小样本、非线性、高维模式的识别中具有很大优势,广泛用于文本识别[2],DNA 分析[3],面部识别[4]等领域。
传统的支持向量机或者针对某类样本进行优化的支持向量机如果直接用于带钢表面缺陷分类时,往往会出现泛化性能差,过度学习,识别率低等问题。 本文采用了遗传算法(Genetic Algorithm,GA)对SVM 进行优化,系统研究了将遗传算法与SVM 方法结合起来用于带钢表面缺陷分类的过程,采用加州大学欧文分校(UCI)标准数据库提供的真实生产数据进行方法验证, 并且与传统SVM 以及BP、LVQ 神经网络、ID3 决策树进行比较研究,从而对带钢表面分类问题中GA-SVM 方法的应用进行科学评价。
1 算法原理
1.1 支持向量机(SVM)
支持向量机的原理是找到一个分类超平面作为决策曲面,最大化正例和反例的隔离边缘。 支持向量机基于结构风险最小化的原则,不利用领域内部问题,在分类问题上具有良好的泛化性能。 支持向量机有着通用性强,鲁棒性高,计算简单等优点。 具体形式如下:
其中为核函数,对于径向基核函数(RBF):
构造决策函数:
以上模型是二分类器,本文通过一对一法实现将二分类器构造为多分类器,即对于样本中任意两种类别均构造一个两分类器,这样共有个两分类器,对某个样本分类时选取所有二分类器分类结果最多那个类别作为该样本的类别。
1.2 遗传算法(GA)
遗传算法(Genetic Algorithm,GA)[5-6]是模仿自然界生物遗传进化过程中“物竞天泽,适者生存”的原理,开发出的一种全局优化随机搜索算法。 该算法由J.Holland 教授于1975年提出,具有应用广泛,使用简单,鲁棒性强等特点。 它借用了生物遗传学的观点,通过自然选择、交叉、变异等遗传操作,实现各个体适应性的提高。 算法拥有一群个体组成的种群每个体在种群演化过程中都被评价优劣并得到其适应值,个体在选择、交叉以及变异算子的作用下向更高的适应度进化以达到寻求问题最优解的目标。
2 建立GA-SVM 仿真模型
2.1 GA-SVM 模型的确定
传统的SVM 也可用作分类器, 然而由于无法确定相关参数的最优取值,所以分类效果不理想。 利用GA 对SVM 进行优化,主要优化式(2)中的惩罚参数C 和式(3)中的核函数参数,确定这两个参数的取值,从而使SVM 分类器具有较高准确率。 传统的网格搜索优化法运行时间长,搜索效果不好,本文利用GA 算法对这两个参数进行优化,采用10 折交叉验证法下的SVM 分类准确率作为遗传算法函数适应度值,这样可以有效地避免过度学习和欠学习的发生,结果具有说服性。在GA-SVM 模型中,每个粒子对应一组C、g 的取值,算法的基本步骤如下:
1)读取样本数据并进行预处理,采用10 折交叉验证法将样本分组,初始化种群;
2)对于当前取值的C、g,利用训练集进行模型训练,并记录该C、g 下的适应度函数;
3)进行组合交叉,变异操作,进一步搜寻更佳的C、g 取值;
4)重复步骤2、3,直到满足最大进化代数。
2.2 GA-SVM 模型优化仿真
本文采用UCI 数据库提供的带钢表面缺陷数据,该数据集来自实际生产, 将带钢表面缺陷分为7 类典型的缺陷,分别为斑点,气刀纵痕,气刀斜痕,亮点,粗渣粒和凸起以及其他缺陷。该数据集共有1 941 组样本,对缺陷图像提取了包括灰度直方图,纹理特征,投影量,图形状4 类共27 种特征。
模型仿真利用林智仁教授开发的LibSVM 工具箱, 使用Matlab 软件进行遗传算法优化支持向量机模型的建立和训练。 遗传算法的参数设置如下:种群数量为20,交叉概率为0.7,交换表一概率为0.8,反转变异概率为0.3,新增概率为0.3,最大进化600 代,核函数选择径向基(RBF),得到SVM最优惩罚参数C=3.73419,最优核函数参数g=0.3657。 将此参数用于数据集的训练和分类, 采用10 折交叉验证法下的分类的结果如表1 所示。
从表1 中可以看到,GA 优化SVM 分类器的分类准确性大多维持在80%以上,第7 个缺陷类别由于代表了其他缺陷类别因而分类准确率较低。
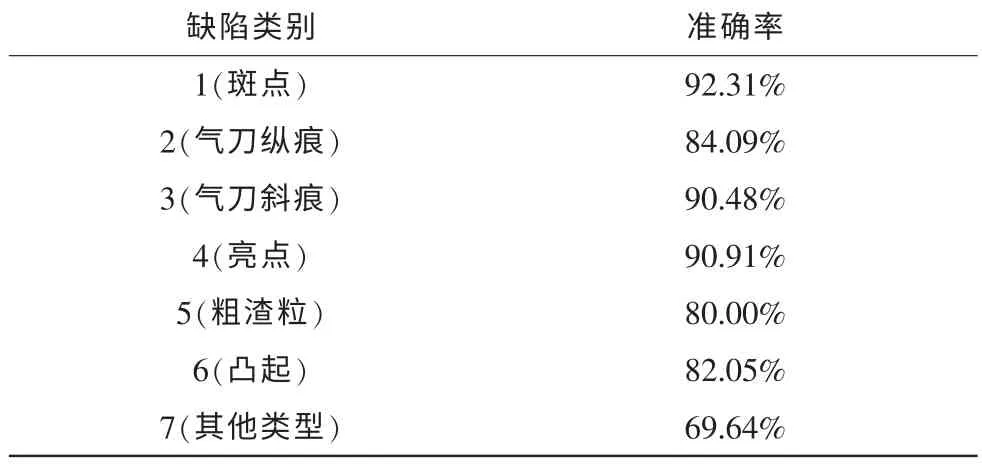
表1 分类准确率表Tab. 1 Classification accuracy rate
3 结果分析
为了进一步验证遗传算法优化支持向量机的优越性,将GA-SVM 方法与传统SVM 分类器进行对比, 分析GA-SVM方法的优越性。 传统SVM 分类器采用在[0,100]的范围内随机生成的参数C、g,对比结果见图1。

图1 随机参数与GA-SVM 优化参数准确率对比图Fig. 1 Classification accuracy rate of PSO-SVM and SVM with random parameters
图1 中黑色折现代表经过遗传算法优化的支持向量机分类器对于每一类缺陷的分类准确率,方块,圆形,三角符号代表的数据分别表示三组随机生成参数的SVM 分类准确率,随机得到的参数分别为第一组:C=70.6046,第二组:g=3.1833;C=19.2837,g=2.0756; 第三组:C=54.7216,g=13.8624。所有仿真实验数据均采用10 折交叉验证法得出分类准确率。 可以明显看出, 虽然有个别随机参数的缺陷准确率比GA-SVM 高,但是这些个别的高准确率实际上是由于判别样本少造成的。整体来看GA-SVM 的准确率大都保持在80%以上,可见本文采用遗传算法对支持向量机分类器进行优化是有效的。
图2 所示为GA-SVM 与其他三种常用算法的分类准确率比较。 比较的对象分别为BP 神经网络,LVQ 神经网络和ID3 决策树算法, 对比各算法对于每一缺陷类别的分类准确率, 依旧采用10 折交叉验证法下的分类准确率。 图2 中可见,经过遗传算法优化的支持向量机分类器的分类准确率相较其他三种算法更高, 平均分类准确率达到83.62%, 而BP神经网络,LVQ,ID3 的平均分类准确率分别为63.09%、74.90%、70.36%。由此可见,GA-SVM 模型能够更准确地对缺陷类型进行分类预测,对于带钢表面缺陷分类问题,GA-SVM方法相较其他方法具有一定的优越性。

图2 4 种算法分类准确率对比Fig. 2 Classification accuracy rate of four kinds of algorithms
4 结束语
带钢表面缺陷的准确分类,是带钢在线检测技术的重要环节。 传统分类方法在处理多分类问题时有一定局限性。SVM 算法具有很强的非线性建模能力,主要根据所提供的生产数据,通过学习和训练找到输入数据与输出数据之间的潜在关联,从而对新样本进行预测。 本文将遗传算法与支持向量机相结合, 采用10 折交叉验证法下的分类准确率作为遗传算法适应度,充分发挥了SVM 方法的非线性建模能力,同时规避了随机设定SVM 参数的盲目性, 提高了模型的泛化能力。 通过与传统SVM 分类器以及其他分类算法的比较,GA-SVM 对于带钢表面缺陷多分类问题效果更优。
[1] 魏 烈 省. 冷轧钢带表面缺陷分析[J]. 钢铁,2006,41(2):386-388.
WEI Lie-sheng. Analysis of surface defects of cold rolled steel strip[J]. Iron and Steel,2006,41(2):386-388.
[2] 高学,金连文.一种基于支持向量机的手写汉字识别方法[J].电子学报,2002,30(5):484-487.
GAO Yue,JIN Lian-wen. A handwritten Chinese character recognition method based on support vector machine [J].Electronic Journal,2002,30(5):484-487.
[3] A Zien,G Ratsch,S Mika,et al. Engineering supportvector machine kernels that recognize translation initiation sites[C]//Bioinformatics,2000,16(9):799.
[4] Y Li,S Gong,J Sherrah,et al. Support vector machine based multi-view facedetection and recognition[J]. Image and Vision Computing,2004,22(5):413-427.
[5] JHHolland. Ada Ptationin Natural Artifieial Systems [M].MITPress,1975:1-17.
[6] 黄少荣. 遗传算法及其应用[J]. 电脑知识与技术,2008,4(7):1874-1875.
HUANG Sao-rong. Genetic algorithm and its application[J].Computer Knowledge and Technology,2008,4(7):1874-1875.

