傅里叶变换在人眼轮廓拟合和人眼几何参数计算中的应用

魏 博，李战明

（兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050）

在数字图像处理和模式识别中，经常需要对图像的轮廓进行分析。在分析过程中，需要预先对图像做一些必要的分析和处理，从而得到图像的轮廓，此时得到的图像轮廓其实是一些孤立的像素点，要对图像的轮廓进行分析和描述就要建立这些像素点的数学模型。针对于某些具有特定的形状的图像例如圆形、直线等可以用最小二乘法拟合这些图像轮廓的方程，进而分析它的某些几何特性，例如长度、面积等。文献[1]中介绍了一种用最小二乘法拟合椭圆方程的方法。然而，对于某些不具有明显几何特征的轮廓，可以采用链式编码[2]描述图像轮廓，但这种方法不能直接计算图像中的几何特征。本文介绍的基于傅里叶变换的图像轮廓描述方法可以将图像的轮廓用傅里叶系数表示，这种方法可以描述任意图像的轮廓，对于具有平滑边缘的轮廓用很少的参数就可以达到很好的描述效果。由于人眼边缘通常是光滑的，而且人眼轮廓具有明显的几何外形，因此这种方法可以很好地用来拟合人眼。而且用一次谐波拟合的人眼，其傅里叶系数具有明显的几何意义。因此可以用这些系数来计算人眼的几何参数。由于傅里叶变换的各种算法在计算机程序设计中得到了广泛的使用，因此，这种方法的计算效率也较其他方法高。

1 原 理

在傅里叶变换描述图像轮廓的方法[3]中，一般将图像定义在复平面内，那么图像中的每一个像素都可以用一个复数来表示。像素的第一个坐标表示复数的实部，第二个坐标表示复数的虚部。因此，轮廓可以表示为下面的形式

图1给出了用复数表示图像轮廓的实例

图1图象轮廓在复平面的表示及其分解Fig.1 The representation of image contour in complex plane and its decomposition

图中用两个周期分别描述了复数实部和虚部的变化函数。通常周期T=2π，导出角频率ω=1。但需要注意的是这种方法只能描述闭合的图像轮廓。

实部函数和虚部函数可以分别展成傅里叶级数

为了获得图像轮廓的傅里叶描述，我们需要求出实部函数和虚部函数的傅里叶系数，其复平面的傅里叶系数可以表示为

为了便于计算机求解，傅里叶系数还可以表示成三角函数的形式，设

由（4），（5）和欧拉公式[4]可得

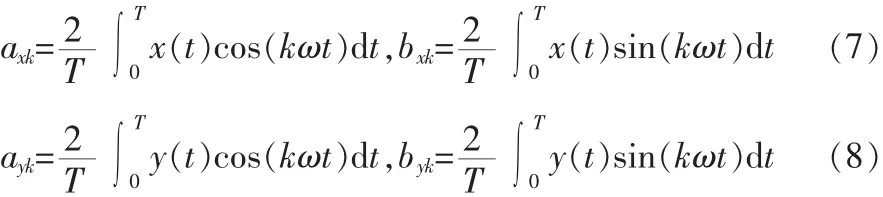
综合式（1）~（8），可以将图像的轮廓表示为傅里叶级数的形式

也可将（9）表示为矩阵形式

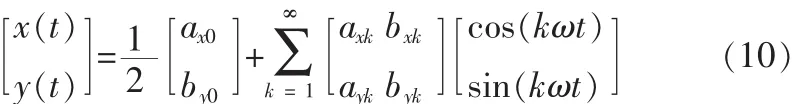
如果仅取傅里叶级数的一次谐波，（10）变为

设任意椭圆的参数方程为

由（11）和（12）可得到以下关系式

小曲（13）-（14）的三角函数项，可得

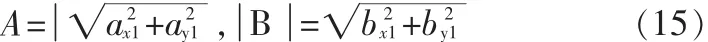
图2一次谐波拟合轮廓的几何图形Fig.2 Shape represented by the first harmonic

图2中显示了上述参数的几何意义

从图中可以看出，由一次谐波的4个傅里叶系数ax1，ay1，bx1，by1可以分别求出椭圆的长轴和短轴的距离。将一次谐波的情形推广到k此谐波，会得出同样的结论。所以，图形轮廓可一描述为一系列椭圆的叠加。通常，低频谐波描述出图像轮廓的整体特征，而高频谐波描述细节特征。人眼轮廓具有明显的整体特征，而且轮廓的边缘很光滑。因此，可以判断用很少次数的谐波就可以准确地描述出人眼轮廓。此外，由于傅里叶变换的系数具有旋转不变和平移不变的性质[5]，所以轮廓的几何参数不受坐标平移和坐标旋转的影响。

2 方法与实验

2.1 人眼轮廓的几何模型与几何参数

由于人眼的轮廓通常是光滑，所以可已将人眼的轮廓近似为椭圆如图3。在某些应用中常要求出人眼的几何特征，如人眼长度（2A）以及人眼宽度（2A），有时还会计算人眼的面积，在人眼疲劳检测[6]中还会用到人眼的长短轴之比S=A/B。但是无论用到哪种几何参数，人眼长度和人眼宽度是两个最基本的参数，其他参数均可由这两个参数导出。

图3人眼的几何模型及其参数Fig.3 The geometric model and parameter of human eyes

2.2 实验与结果

在用傅里叶变换描述人眼轮廓时，首先要用到一些方法提取人眼轮廓，本实验先用Candy算子[7]的方法得到了人眼图像的边缘，然后用数学形态学的方法[8]处理此前得到的图像，最终获得了人眼的轮廓图。得到的人眼的轮廓可以看成一个有限点集，表示为 A={（x，y）|（x，y）{人眼边界}}。图 4（a）中显示原始的人眼灰度图，图4（b）是经过处理的人眼的轮廓图。

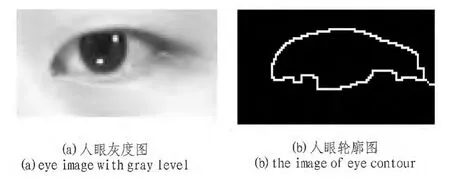
图4人眼的预处理Fig.4 The preprocessing of eye

得到人眼轮廓的集合A后，可以将这些点集描绘到复平面内。如图5，图中的坐标系采用了图像坐标系，即x轴的正方向同笛卡尔坐标系一样是从左到右的，y轴的正方向则与笛卡尔坐标系相反是从上到下的。图中的圆圈表示绕图像轮廓旋转的起点，旋转方向是逆时针。由于噪声和光照等因素的影响，从图中可以看出同人眼灰度图相比，这里得到的轮廓中，人眼的下边缘不太光滑，出现了一些明显的波动。

图5复平面内的人眼轮廓Fig.5 Eye contour placed in a complex plane

由方程（1）可知，可以将人眼轮廓的二维坐标（x，y）分别分解到实轴和虚轴上，得到图6所示的两条曲线。第一条曲线纵坐标x（t）表示在轮廓上旋转两周，人眼轮廓在实轴上的投影，横坐标表示旋转的弧度。同样的，第二条曲线y（t）的表示旋转时在虚轴上的投影，横坐标表示旋转弧度。此处旋转的角速率ω=1。

图6人眼轮廓在复平面的投影曲线Fig.6 The projected curves of human eyes in a complex plane

从图中可以看出x（t）曲线的形状与三角函数的形状很接近，而y（t）曲线在后半个个周期内出现了小范围的高频波动，而在前半个周期内与三角函数也非常接近。比较两幅图发现，实轴投影图（a）的幅值范围要比要比虚轴投影图（b）的范围大得多，这与在图5中观察到的情形是一致的。

在得到实轴和虚轴上各自的函数后，可以根据（7）~（8）计算出各自的傅里叶系数，图7绘出前十次谐波的傅里叶系数的直方图，其中k={1，2，...，10}表示谐波次数。比较四幅图可以看出在五次谐波以后，傅里叶系数出现了明显的衰减。也就是说，五次以后的傅里叶系数对图象轮廓的贡献率已经很小，可以忽略不计。 从图中还可以看出，ax（k），ay（k）和by（k）的一次谐波幅值的绝对值明显比其他次谐波的幅值的绝对值大得多，这说明一次谐波的傅里叶系数在描绘人眼轮廓时占据主导地位。但是在傅里叶系数ay（k）中，二次谐波系数的数值最大，其他谐波系数出现了很大程度的衰减。这表明在虚轴上的投影有明显的的二次余弦谐波分量。

求出各次谐波的傅里叶系数后，既可以用它来合成人眼的轮廓也可以计算人眼的几何参数。在图8中，虚线表示用一次谐波拟合成的人眼轮廓，实线是用前五次谐波你合成的人眼轮廓。从中可以看出用一次谐波就可以拟合成出人眼的大体轮廓，根据图2的几何关系，一次谐波系数可以近似计算出人眼的长度和宽度，也可以导出其他几何参数。在实际应用中，如果是计算人眼的几何参数，可以用一次谐波拟合的曲线做近似计算。如果是恢复人眼轮廓，可用更高次的谐波拟合。除此之外，用傅里叶变换拟合轮廓还可以除去轮廓边缘的噪声。同图5相比，用前5次谐波拟合的人眼轮廓的边缘明显变得光滑了。在提取人眼轮廓是，人眼轮廓是否精确也影响着人眼的拟合效果。图8中用五次谐波拟合的人眼轮廓与图4a中相比还是有明显的误差，这说明这种方法可以有效的去除图像轮廓的高频噪声，如边缘的局部抖动以及毛刺等，但对于引起图像轮廓变形的低频噪声却无能无力。因此，前期轮廓提取的准确性是很关键的，尤其注意要避免低频噪声。

图7傅里叶系数的直方图Fig.7 The bars of Fourier coefficient

图8傅里叶系数拟合的人眼轮廓Fig.8 Fitting the eye contour using Fourier coefficients

3 结束语

通过上述分析可知，在已知人眼轮廓点集时，傅里叶变换可以用来拟合人眼以及分析人眼轮廓的几何参数。由于人眼轮廓通常是平滑的，傅里叶变换也可以对人眼轮廓起到平滑和去噪的作用。同其他轮廓拟合和几何参数分析方法相比，此种方法的算法跟容易实现，而且算法效率更高。因此，可以得到广泛的应用。

[1]Anandaroop Ray，Srivastava DC.Non-linear leastsquaresellipse fitting using the genetic algorithm with applications to strain analysis[J].Journal of Structural Geology，2008，30（6）:1593-1602.

[2]Walid Shahab，Hazem Al-Otum，Farouq Al-Ghoul.A modified 2D chain code algorithm for object segmentation and contour tracing[J].The International Arab Journal of Information Technology，2007，6（3）:250-257.

[3]Mark S.Nixon，Alberto S.Aguado.Feature Extraction and Image Processing[M].Second Edition.London:Elsevier，2008

[4]苏变萍，陈东立.复变函数与积分变换[M].北京：高等教育出版社，2003.

[5]胡广书.数字信号处理-理论与、算法与实现[M].2版.北京：清华大学出版社，2003.

[6]Robinson Jimenez，Flavio Prieto，Victor H.Grisales.Detection of the tiredness level of drivers using machine vision techniques.Electronics，Robotics and Automotive Mechanics Conference[C].Cuernavaca:Mexico，2011.

[7]John Canny.A computational approach to edge detection[J].Transactions on Pattern Analysis and Machine Intelligence，1986，8（6）：679-698.

[8]Dr.Pierre Soille.Morphological Image Analysis:Principles and Applications[M].Second Edition.Berlin:Springer，2004.