促进数学课堂生成 提高教学有效性
邱祥成

生成是新课程教学的一个亮点,它体现了课堂教学的丰富性、开放性、多变性和复杂性,激发了师生的创造性和智慧潜能,使课堂教学焕发出了生命力.[1]笔者结合自己的教学经验,从捕捉有价值“错误”、抓住意外的“契机”、留给学生思考的空间以及有效追问四个方面来论述如何促进数学课堂生成,因势利导提高教学有效性.
一、捕捉有价值的“错误”
教师要正确面对学生的错误,因为错误也是一种教学资源.正因为出错,才会有点拨、引导、解惑,才会有教育的敏感、机智和智慧,才会有对学生乐观的期待,以及真正的爱护和保护.[2]只有出了错,课堂才能生成.在“出错”和“改错”的探究过程中,课堂才是最活的,教学才是最有魅力的,学生的生命才是最有价值的,所以教师在课堂上要及时捕捉有价值的“错误”.
案例1 在一元二次方程的复习课中,有这么一道题:已知关于x的一元二次方程(1-2k)x2-2 x
-1=0有实数根,求k的取值范围.
教师出示这道题后,好多同学都流露出欲欲跃试的表情,最后老师请了生1到黑板演示解题的过程.
解:∵一元二次方程有实数根,∴b2-4ac≥0.
∴(2 )2-4×(1-2k)×(-1)≥0,得
∴k≤1.
教师待生1演示完后,并没有立刻评价生1的答案,而是转向全班同学说:同意生1的答案的同学请举手,结果有一些同学举起手来.教师没有责怪学生做得不对,相反觉得这是一个很好的纠错机会,这时下面已经有学生叫起来说黑板的答案不对,教师因势请生2来发表自己的看法.
生2:由题意可知,此方程是一元二次方程,所以要求二次项系数不等于零,(1-2k)≠0,即k≠ ,所以正确的答案是k≤1且k≠ .
这时有好些学生都给生2投以赞许的目光,教师也适时给以肯定,但就在这时候生3把手举得极高,说生2的还是不对,这时很多学生都流露出极其疑惑的表情,教师又趁机请生3来发表自己的看法.
生3:我觉得二次根号被开方数要大于等于零,一次项系数2 中的k要满足k≥0 ,所以正确的答案是:0≤k≤1且k≠ .
这时教室响起一阵热烈的掌声,教师也立刻给肯定,表扬了生3考虑问题考虑得很全面. 经过这“一波三折”,全班学生都认识到出错的原因,成功纠错.
由这个案例可以看到,学生出现的错误,具有一定的典型性、代表性. 因此教师要用敏锐的目光捕捉学生错误中的生成资源,并且充分地利用这种资源,让学生积极参与到教学中去. 通过对错误地修正、探究,使学生掌握知识,同时也培养了学生勇于探索的精神,从而使课堂的作用得到最大的发挥.
二、抓住意外的“契机”
在课堂上,教师面对的是一群有着不同生活经历、在很多方面存在着差异的个体. 也正是因为有这些差异,课堂才是充满变化的,有着各种“意外”的出现. 这些“意外”可以激发学生热情和挑战的情绪,只要抓住这个意外的“契机”,促进课堂新的生成,将会收到意想不到的教学效果,课堂教学也因此变得更加精彩、更加有效.
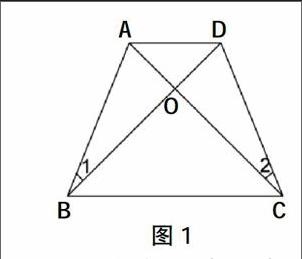
案例2 在学习梯形的性质的时候,在课堂上出现了这样一道题:如图1,在等腰梯形ABCD中,AD∥BC, AC⊥BD,若AD=3 cm,BC=5 cm,求这个梯形的面积.
教师设计这道题的本意是让学生熟悉梯形的面积公式:S梯形= (上底+下底)×高,出示这道题五分钟后,教师对全班同学说:“这道题做完的同学请举手.”令教师吃惊的是,居然没有人举手.这时教师心里充满疑惑,但是他并没有立刻责怪学生,而是看了一下自己出示的题目,发现原来是自己出示这道题的时候漏掉了“AB=CD= ”这个条件.此刻教师心里暗喜,但并没有给学生补上这一条件,而是故意说:“其实这道题我也还没解出来.”这时班上已经有学生叫起来了:“老师都不会做.” 然后教师说:“你们要不要试试.”学生大声说“要.”教师知道这时已经激起他们的挑战心理,有些学生肯定在想:“老师不会做的题目,我如果能做出来,多牛啊.”全班都很认真在思考,寻找解题的方法,大概又过了十分钟,有个学生举手说他解出来了,这时全班一阵雀跃. 教师趁机说:“那么我们请这位同学来讲解他的解题思路.”以下是这位学生的解题思路:
第一步:证△ABD≌△DCA 得∠1=∠2;
第二步:证△AOB≌△DOC得OA=OD,OB=OC;
第三步:在Rt△AOD和Rt△BOC中利用勾股定理求得OA=OD=3,OB=OC=5,因而AC=BD=8;
第四步:S梯形=S△ACD+S△ABC= AC·OD+ AC·OB= AC(OD+OB)= AC·BD.
待这位学生讲解完后,全班学生都惊呼:太厉害了!此时班里响起更热烈的掌声,教师觉得这个意外的效果收到了(此时教师让学生自己写一遍解题过程),接着教师引导学生继续总结:
师:这个同学有没有使用梯形的面积公式进行计算啊?
生4:没有.
师:那他是用了什么样方法来求梯形的面积?
生4:把梯形ABCD分成两个三角形△ACD和△ABC来求.
师:那从这道题看来,我们在求梯形的面积可以有哪些方法?
生4:可以用梯形的面积公式,或是把梯形分割成几个三角形.
师:由此看来,求图形面积时,如果不能直接用公式求的话,可以采用什么方法进行求解?
生4:可以把图形进行合理的分割.
师:我给大家做这道题时,不小心写少了AC=BD= .
生4:啊?太简单了,只要把高求出来,就可以直接用梯形的面积公式了.endprint
师:我今天对大家的表现非常满意.
可见,教师抓住有价值的“意外”,适时调整课堂的教学行为,教师放下“面子”,极大地刺激了学生的挑战心理,通过学生独立思考,挖掘自己的潜能,终于挑战成功,极大地满足了学生的自信心.也因此由学生发挥主体的能力,促成了新的生成点,造就精彩的课堂.
三、留给学生思考的空间
在传统教学中,经常出现满堂灌的情况,教师经常牵着学生的鼻子走,学生基本没有自己独立思考的时间. 往往教师把问题抛出来,在很短的时间内就要求学生回答,更有甚者就是自问自答. 这样造成的结果就是教师是课堂的主体,教师可以顺利完成他自己的预设,而学生只是被动地接受.这不符合课程标准要求的把课堂还给学生,实际上只有把学生当作课堂的主体,给以学生思考的空间,才会有因学生认知水平而产生有价值的生成,这样的课堂才更加有效.
案例3 “三角形全等的条件”的教学片段
师:我们已经知道用“边角边”可以判定两个三角形全等,那么当这里的角不是两边的夹角,而是其中一边的对角时,两个三角形还全等吗?
学生开始在练习本上画图、尝试、并和同桌交流.很快大家纷纷表示这种方法不能判定两个三角形全等.
突然,生5大声道:“是全等的!”
师:请你说说自己的想法.
生5:我是用直角三角板来画的(如图2),先画出∠C=∠F,然后截取AC=DF,AB=DE,这样画了几次都是全等的.
师:很好!现在请大家也用直角三角板来画一画,看看是否全等.
学生纷纷用直角三角板画三角形进行验证,结果所画的两个三角形确实是全等的,从而与前面得出的结论产生了矛盾,学生开始思考、讨论.
生6:我觉得这样画不是很好,画出来的都是直角三角形,这只能说明在直角三角形中是成立的.
师:不错!这样画出的三角形确实都是直角三角形,这至少说明在直角三角形中,两边和其中一边的对角相等的两个三角形是全等的.那么对于任意三角形,能不能用“边边角”来判定全等?
学生又开始讨论探究,结论是“边边角”不能判定三角形全等(如图3),∠B=∠E,AB=CD,AC=DE.
师:如果不指明是哪类三角形,“边边角”能判定全等吗?
生7:不能!
在此案例中,教师原本只想让学生通过动手操作得到“边边角”不能判定三角形全等,但是学生的一次特殊操作(利用直角三角板来画)得到了全等三角形,改变了教师的预设,教师抓住这个宝贵的生成,及时调整预设,自然地让学生探索“边边角”在什么情况下是成立的,在什么情况下是不成立的,使学生的探索有了深度,从而对三角形全等的判定有了更深的认识. 从此案例也发现只要留充足的时间和空间给学生思考,就可以让你的预设得到很好的生成,同时也培养了学生积极思考探索的能力,让你的课堂处处体现学生的主体性,整个课堂充斥着学生思维的光芒.
四、有效追问
课堂教学是师生、生生之间有效互动的生成过程,强调课堂教学的生成性.[3] 课堂教学活动是师生生命活动的展现. 教师在有效追问的观念指导下,课堂教学中教师要对学生的反应保持敏感,及时进行有效的“追问”.
案例4 在复习“相似三角形”时,教师出示题目:如图4,在直角梯形ABCD中,AD∥BC,∠A=∠B=90°,∠DEC=90°,试说明AD,AE,BE,BC之间的关系.
因为对图形很熟悉,学生很快就说出这四条线段的关系:由△ADE∽△BEC得 = .
追问1:若去掉AD∥BC这条件,把这个图中的三个90°改成60°(如图5),这四条线段有什么关系?
学生试着用解原题时找相等角的方法,证得△ADE∽△BEC,从而得到四条线段成比例的关系: = .
追问2:如果再把60°改成110°(如图6),是否有相同的结论呢?
学生经过片刻思考,马上得到肯定的回答:四条线段有相同的关系.
追问3:现在你们有什么发现?
学生经过思考,最后得到当∠DEC=∠A=∠B时,都能证得△ADE∽△BEC,从而得到 = .
在上述案例中,教师通过有效的变式追问使学生掌握了方法,熟悉了图形特征,拓宽了思考问题的思路.正因为教师的有效追问,引发学生的思考,不断促进课堂新的生成,体现了课堂中师生有生命力的互动,从而提高了教学的有效性.
新课程要凸显教学的生成性,因而教师应在关注学情的前提下精心预设,在互动对话中善于去捕捉、发现和重组课堂教学中从学生那涌出来的各种各样的信息,而且要对这些信息进行梳理,然后把有价值的信息和问题转化为教学问题,纳入教学内容,成为教学的闪光点,并把它转化为学生智慧发展的“火种”,以达到努力追求富有活力的课堂生成,构建真正意义上的有效课堂之目的.
参考文献:
[1] 余文森. 有效教学十讲[M]. 上海:华东师范大学出版社,2009:25.
[2] 陈新芸.实施有效追问,构建生命课堂[J].初中数学教与学,2010(9):23.
[3] 朱生权.初中数学课堂提问有效性探索[J].初中数学教与学,2010(12):12-13.endprint

