整体叶盘电解加工组合式阴极结构优化及试验研究
邓守成,刘 嘉,朱 栋,朱 荻
(南京航空航天大学机电学院,江苏南京210016)
整体叶盘是为了提升航空发动机性能而设计的一种新型结构件[1]。它将叶片和轮盘做成一体,替代了榫头与榫槽通过锁片连接的方式,使其结构简化、重量减轻、可靠性增强。整体叶盘结构复杂,叶片超薄、扭曲,叶间通道狭窄,通常选用钛合金、高温合金等难切削材料,加工精度要求苛刻,制造十分困难。电解加工是基于电化学阳极溶解原理去除材料的一种工艺方法,具有工具无损耗、加工不受金属材料本身力学性能的限制、加工效率高等特点,被广泛应用于航空航天、兵器、模具等领域[2-3],是整体叶盘等难切削复杂零件理想的制造加工工艺[1]。美、英、俄、德等航空制造强国都将电解加工作为航空发动机整体叶盘制造的主要方法,包括中国在内的专家学者都对整体叶盘电解加工技术开展了大量研究,如:群电极多通道加工、径向进给通道加工、数控展成电解加工、W型流场型面电解加工及三维复合流场型面电解加工等[4-10]。
在电解加工中,工件型面的成形是由阴极形状保证的,阴极变形是影响加工精度与重复性的重要因素。由于整体叶盘结构复杂,叶间通道狭窄,容纳阴极的加工区空间非常狭小,工具阴极受空间限制较为单薄,阴极整体刚性不高。同时,整体叶盘阴极结构复杂,薄片状的工具阴极通过咬合结构将叶盆、叶背阴极组合在一起[11],组合式的阴极结构使两个阴极刚性相互影响与制约,若两个阴极刚性分布不均,刚性较弱的一方在电解液压力条件下会产生较大变形,使叶片型面的加工精度和重复精度受到严重影响。因此,有必要在有限的阴极整体刚性条件下针对组合式阴极刚性分布进行优化,均衡叶盆、叶背阴极变形量,使两个阴极的刚性同时满足加工需求。
本文以整体叶盘加工组合式工具阴极为研究对象,提出了一种组合式阴极结构刚性优化方法。以叶盆、叶背阴极变形量差值为优化目标函数,求解目标函数的最小值,利用单向流固耦合有限元分析方法分析阴极变形量,采用黄金分割法求解目标函数最小值,最终确定最优的组合式阴极结构。还开展了优化工具阴极的工艺试验,验证优化结果的有效性。
1 组合式阴极变形分析
在整体叶盘电解加工过程中,叶盆、叶背阴极伸入预加工好的叶间通道中,相互面向进给,同时加工叶片毛坯的叶盆、叶背型面。加工方式见图1。
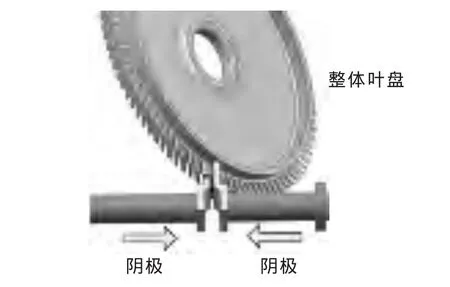
图1 整体叶盘加工示意图
由于整体叶盘结构复杂,叶间通道狭窄扭曲,工具阴极通常设计成薄片状组合式阴极结构[3-4]。由于加工区空间非常有限,无法通过增加阴极厚度来提升刚性,所以组合式阴极整体刚性不强。同时,组合式阴极结构特殊,叶盆、叶背阴极上具有互相交叉咬合的矩形滑块,该结构直接决定叶盆、叶背阴极的支撑端面积,影响叶盆阴极和叶背阴极的受力变形。组合式阴极结构见图2。若咬合结构设计得不合理,极易出现两个阴极刚性分布不均,而刚性较弱的一方在电解液压力条件下会发生较大变形,严重影响电解加工精度和稳定性。因此,为避免上述情况,有必要针对组合式阴极的组合结构进行分析与研究,通过优化组合结构尺寸关系,均衡两个阴极的变形量,在有限的阴极整体刚性条件下减小组合式阴极的变形量。
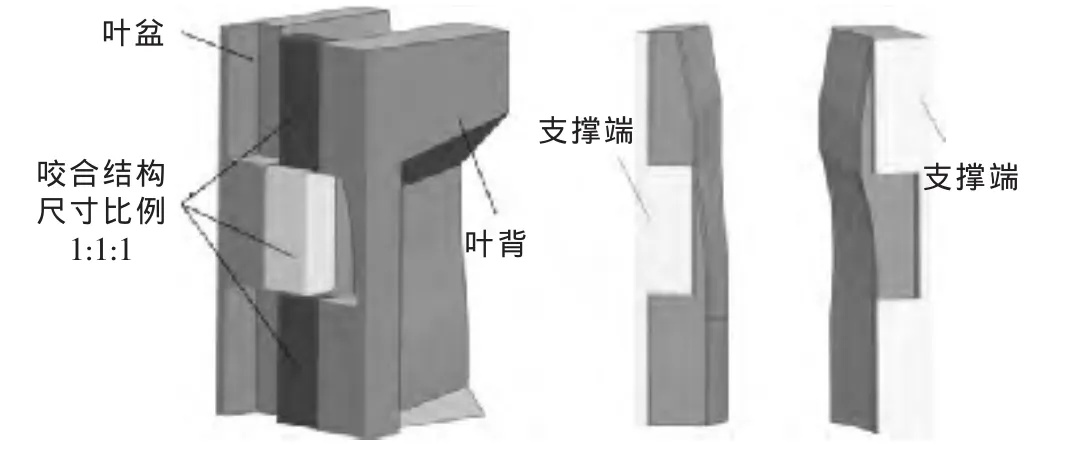
图2 组合式阴极结构
整体叶盘组合式工具阴极,其咬合结构的矩形滑块通常采用等尺寸设计(图2)。为了分析该组合式阴极的刚性,采用单向流固耦合的有限元方法进行分析。在叶盆、叶背工具阴极表面的电解液流体压力分析过程中,基于整体叶盘加工中常用的三维复合流场模式[12]。在有限元流场仿真分析中,为简化计算且不失分析精度,作以下假设:
(1)电解液为理想状态液体,不含气泡、固体颗粒等杂质,电解液的流动特性不受温度等因素的影响;
(2)电解加工处于平衡加工状态,各项参数不随时间变化而只是几何位置的函数,阳极溶解速度与阴极进给速度相等,加工间隙已达到平衡间隙,不再随时间而变化。
有限元流场仿真分析的流道模型见图3a。A为主进液口,压力为0.9 MPa;B为辅进液口,压力为0.5 MPa;C为出液口,压力为0.1 MPa。对流道模型进行网格划分,并对加工间隙处的网格进行细化(图 3b)。
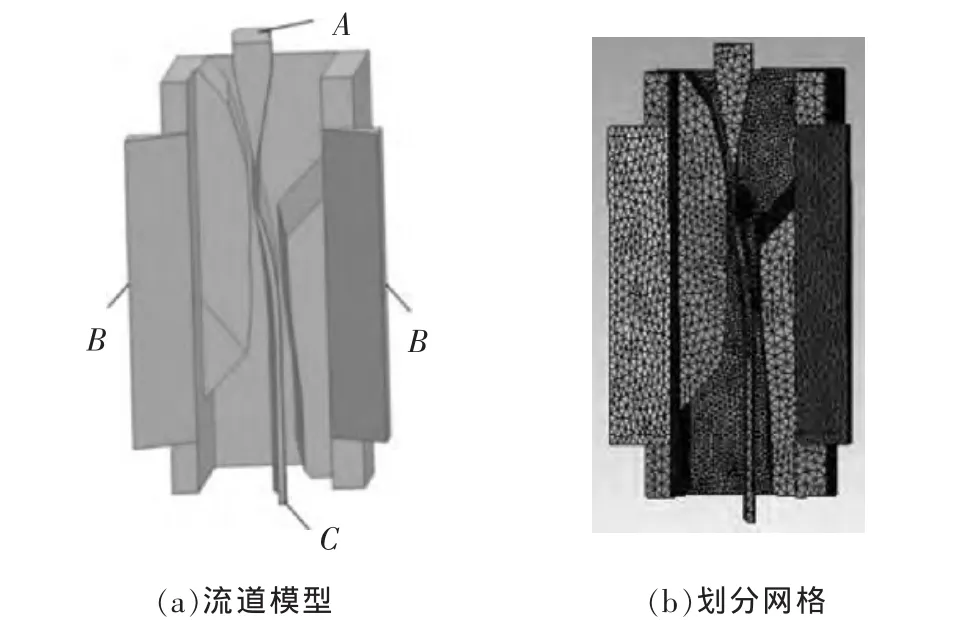
图3 三维复合流场模型
在计算分析中,液体流动的湍流模型选择标准k-ε模型,其对应的输运方程为:
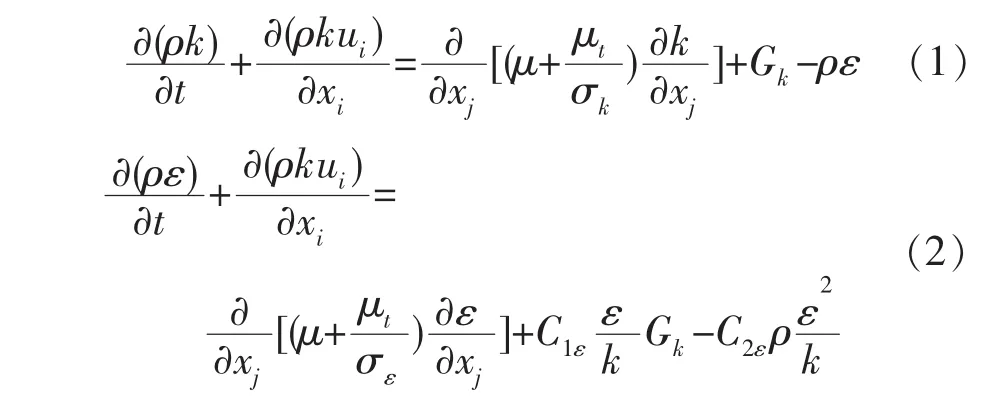
式中:Gk为平均速度梯度引起的湍流动能产生项,按计算;μt为湍动粘度,按 μt=计算; 模型常数 C1ε取 1.44,C2ε取 1.92;σk取1,σε取 1.3。
利用有限元分析方法对图3所示的模型进行求解,得到三维复合电解液流动方式下叶背阴极与叶盆阴极表面的流体压力投影分布(图4)。其中,图4b、图4d分别是电解液在叶背阴极、叶盆阴极非加工面上的压力值,其值较平均,约0.3 MPa。图4a、图4c分别是电解液在叶背阴极、叶盆阴极加工面上的压力分布图,在主液作用下,电解液压力从电解液入口至电解液出口呈逐渐递减趋势。
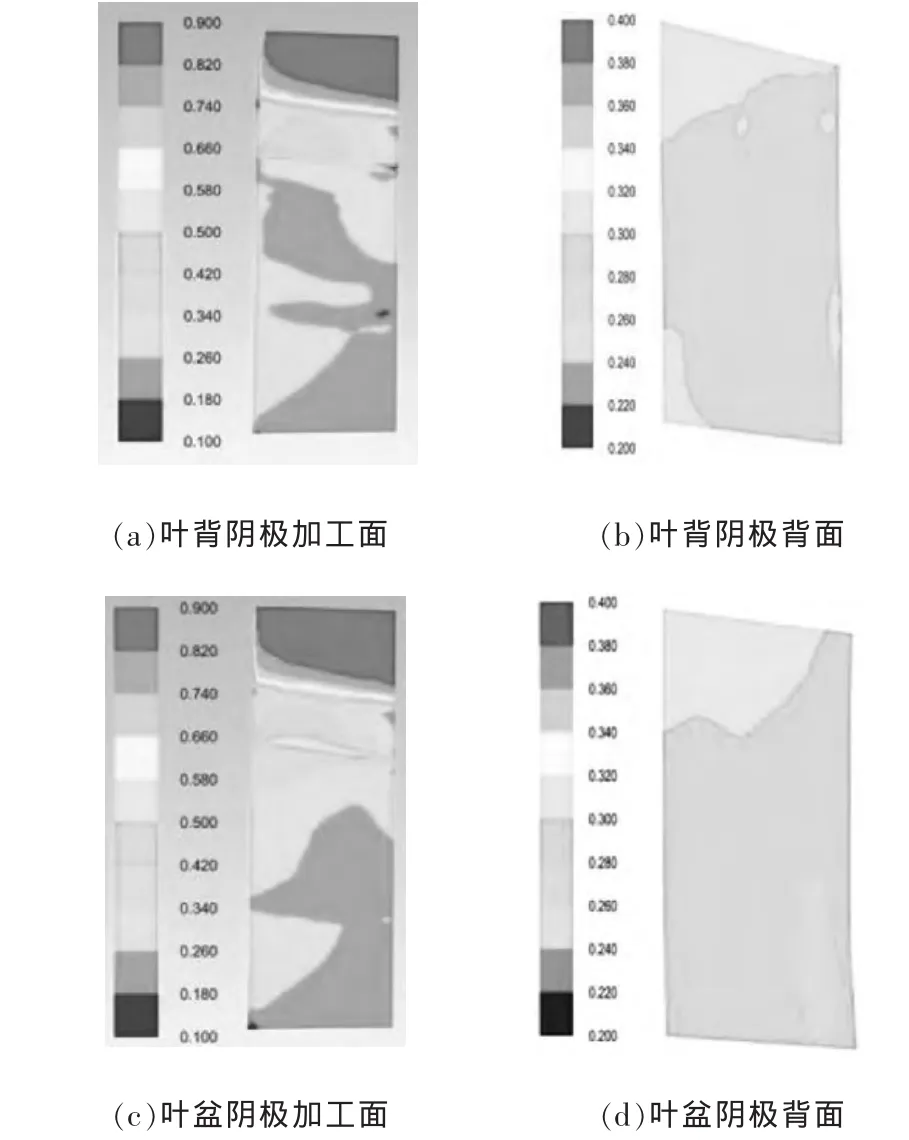
图4 阴极型面上电解液压力分布
依据上述流场仿真获得的工具阴极表面液压力分布结果,采用有限元方法开展固体阴极变形分析,求解出的工具阴极变形结果见图5。从有限元仿真分析结果可知,叶背最大变形量约为0.0054 mm,叶盆最大变形量约为0.0685 mm,叶盆变形量远大于叶背变形量。由此可见,组合式阴极通常采用的咬合等尺寸设计并不合理,会造成叶盆、叶背阴极变形量一方较大、一方较小,叶盆的变形量会对叶片加工型面精度造成严重影响,因此,必须对咬合结构进行优化设计,均衡叶盆、叶背阴极的刚性。

图5 阴极加工面变形量
2 组合式阴极结构优化设计
为解决上述问题,对组合式阴极结构进行优化设计。其中,叶背阴极采用等尺寸双滑块设计,叶盆阴极采用单滑块设计,其结构见图6。不难发现,增大叶盆阴极单滑块的宽度,叶背阴极双滑块的宽度会相应减小,这会使叶盆阴极刚性提升,叶背阴极刚性下降;反之,减小叶盆阴极单滑块的宽度,叶背阴极双滑块的宽度会相应增大,这会使叶盆阴极刚性下降,叶背阴极刚性提升。由此可见,在工具阴极无法通过增大尺寸以增加刚性的情况下,若能找到合适的滑块比例,通过一方刚性增大、一方刚性减小,来改变叶盆、叶背阴极变形量差值较大的情况。均匀化两个阴极的变形量,使组合式阴极整体刚性达到最优。
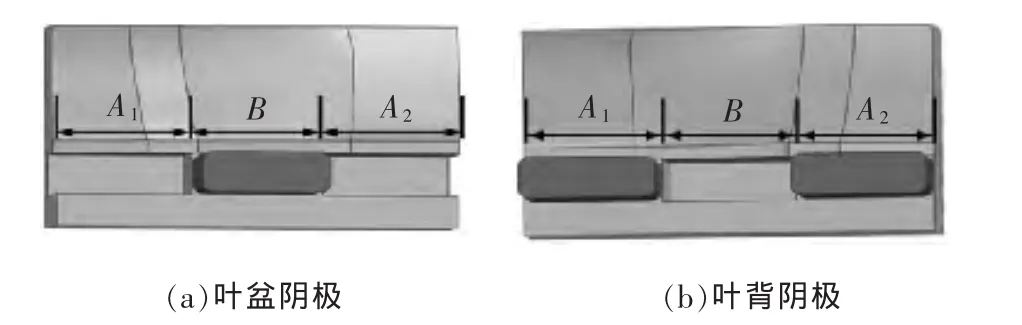
图6 组合式阴极结构
基于上述设想,本文提出了一种组合式阴极刚性优化方法,该方法以叶盆、叶背阴极变形量的差值作为目标函数,其最小值即为最优解。如图6所示,设叶背阴极等尺寸的两滑块宽度为A1、A2,并满足A1=A2,叶盆阴极单滑块宽度为B,阴极总宽度为L,则可知:A1=A2=(L-B)/2,A1与 A2可由 B 表示。 因此,本文设叶背阴极上的单滑块占总阴极宽度的比例(B/L)为目标函数自变量x,函数m(x)为叶盆阴极在该滑块比例下的变形量绝对值,函数n(x)为叶背阴极在该滑块比例下的变形量绝对值,则目标函数为 f(x)=|m(x)-n(x)|。
优化中,函数m(x)与n(x)的值采用有限元单向流固耦合方法求解。目标函数f(x)是单峰函数,采用黄金分割法进行搜索。开始优化前,首先需确定自变量x=B/L的搜索范围。
由于f(x)是连续函数,任意选取两个自变量值a与 b,若 m(a)-n(a)>0,m(b)-n(b)<0,则使 m(x)-n(x)=0的x必定存在于a与b的区间内。本文选择a=1/4、b=3/4,求解得:
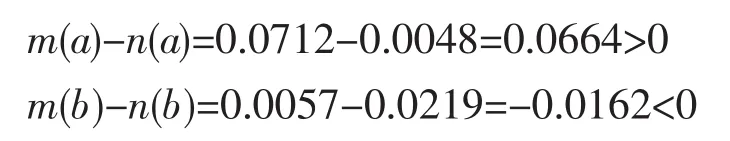
因此,搜索范围[1/4,3/4]有效。采用黄金分割法在该区间内进行搜索,搜索结束判断指标ε取值0.015。其搜索流程见图7,具体计算结果见表1。
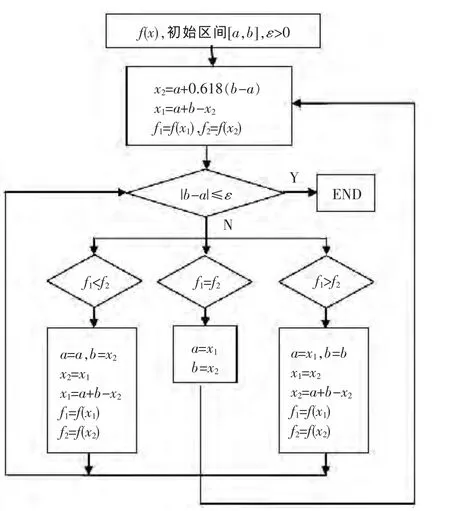
图7 搜索流程
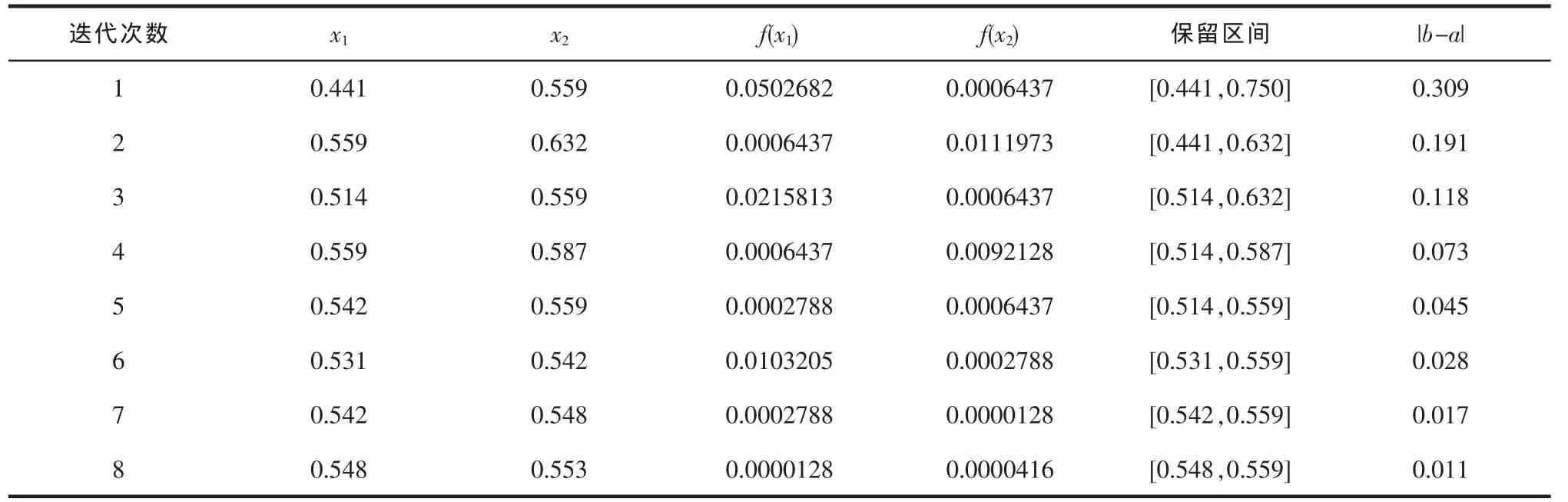
表1 计算结果
当迭代次数为 8 时,|b-a|=0.011<ε, 取最优点x=(x1+x2)/2=0.55,可求解得到最优解 B=44.04 mm,A=35.96 mm。仿真x=0.55时的工具阴极变形量见图8。叶背阴极最大变形量约为n(x)=0.0079 mm,叶盆阴极最大变形量约为m(x)=0.0080 mm,变形量差值 f=|m(x)-n(x)|=0.0001 mm,叶盆与叶背阴极的刚性近似相等,且两个阴极的变形量均<0.01 mm,组合式阴极的整体刚性已能满足加工需求。优化后的组合阴极尺寸见图9。
为进一步验证优化结果的有效性,采用优化获得的最优组合式阴极结构比例开展工艺试验。
3 实验验证
依据优化结果设计的组合式阴极见图10a。工具阴极总宽度L=80 mm,因此可求得叶背滑块宽度B=44 mm,叶盆等尺寸双滑块宽度A1=A2=18 mm。组合式阴极材料为不锈钢1Cr18Ni9Ti,电解加工夹具(图10b)材料为玻璃钢。加工采用三维复合流场方式,流场参数与流固耦合仿真分析中的参数保持一致,主进液口压力为0.9 MPa,2个辅液进液口压力为0.5 MPa,出液口背压为0.1 MPa。电解加工的扇段试件见图11,连续加工了9片叶片。

图8 阴极变形

图9 优化后的组合阴极结构

图10 电解加工阴极和夹具

图11 电解加工扇段
加工时,若工具阴极因刚性不佳发生变形,受其影响最显著的是型面的重复加工精度。为便于分析,在每片叶片的叶盆、叶背型面上,从叶尖至叶根各选取3条截面线,采用三坐标测量机测量每一片叶片的上述6条截面线,9片叶片的截面线重复精度见图12。叶盆型面的加工重复精度为0.04 mm,叶背型面的加工重复精度为0.03 mm。试验样件获得了较好的加工重复精度,说明组合式阴极在加工中具有较好的刚性。试验结果验证了组合式阴极结构优化结果的有效性,证明了优化方法的可行性。
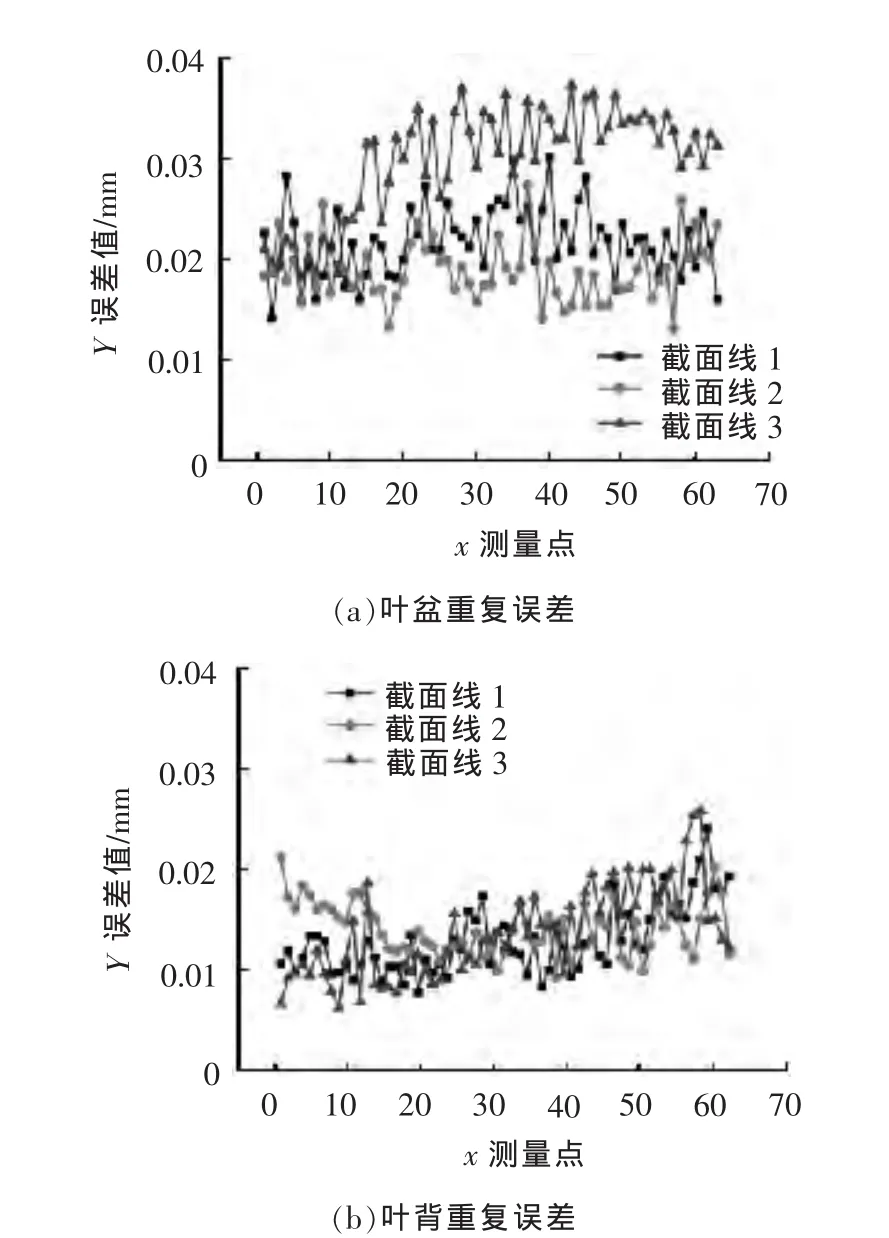
图12 叶片检测误差
4 结论
(1)在整体叶盘电解加工中,受加工区空间限制,组合式阴极的整体刚性不强,且存在叶盆、叶背阴极刚性分布不均,刚性较弱的一侧易发生变形,影响加工精度。
(2)组合式阴极刚性优化方法是以叶盆、叶背阴极变形量的差值为目标函数,其最小值即为最优解。采用有限元流固耦合变形分析与黄金分割法获得了某组合式阴极的最优结构。
(3)采用优化后的组合式阴极开展了多叶片扇段样件加工实验,并获得了具有较好重复精度的样件,试验结果验证了优化结果的有效性,证明了优化方法的可行性。
[1] 史耀耀,段继豪,张军锋,等.整体叶盘制造工艺技术综述[J].航空制造技术,2012(3):26-31.
[2] 朱荻.国外电解加工的研究进展 [J].电加工与模具,2000(1):11-16.
[3] 徐正扬,朱荻,王蕾,等.三头进给电解加工叶片流场特性[J].机械工程学报,2008,44(4):189-194.
[4] Zhu Dong,Zhu Di,Xu Zhengyang,et al.Investigation on the flow field of W-shape electrolyte flow mode in electrochemical machining [J].Journal of Applied Electrochemistry,2010,40(3):525-532.
[5] Zhu Dong,Zhu Di,Xu Zhengyang.Optimal design of the sheet cathode using W-shaped electrolyte flow mode in ECM [J].The InternationalJournal ofAdvanced Manufacturing Technology,2012,62(1-4):147-156.
[6] Hinman E R.ECM machine with skewed workpart and pocketed cathodes:US 4657649[P].1985.
[7] 韦树辉,徐正扬,孙伦业,等.整体叶盘叶栅通道电解加工工具电极进给方向优化设计[J].电加工与模具,2012(4):21-25.
[8] Lamphere M S,Robertson R S,Graham J S.Tandem lisk electrochemical machining:US 2006272957[P].2006.
[9] 朱永伟,徐家文,赵建社.大扭曲度整体涡轮叶片展成电解加工成形规律及试验研究 [J].中国机械工程,2006,17(17):1778-1783.
[10]刘嘉,徐正扬,万龙凯,等.整体叶盘电解加工移动密封阴极设计及试验 [J].中国机械工程,2014,25(14):1847-1851.
[11]徐庆,朱荻,徐正扬,等.整体叶盘通道电解加工电极多维运动轨迹优化[J].航空学报,2011,32(8):1548-1554.
[12]刘嘉,徐正扬,万龙凯,等.整体叶盘叶型电解加工流场设计及实验[J].航空学报,2014,35(1):259-267.

