工程项目任务扰动的综合度量与方案优选

蒋红妍，宗海龙，周 博

(西安建筑科技大学土木工程学院，陕西 西安 710055）

现实生活中，外部环境时时刻刻都在变化，存在着许多不确定性因素.这些因素会干扰事物的发展方向，使其偏离原计划.Yu Gang 等人[1]首次对这一问题进行全面系统定义，提出了干扰管理的概念并给出了研究思路，即需要及时调整计划方案来减小或消除干扰所造成的影响，使干扰产生的副作用最小.Zhu等人[2]从成本最小角度对这类问题进行了研究，利用干扰管理对项目干扰事件迅速响应，实时进行优化调整，并尽可能做到新方案相比原计划扰动成本最小.现代工程项目具有规模大、投资大、周期长、技术复杂等特点，因此在实施过程中也存在着诸多不确定的干扰因素，这将直接或间接地影响项目的顺利进行.

工程项目在实施过程中受到的干扰，主要有项目网络扰动、任务扰动、资源扰动和里程碑扰动等[3].实践中，遇到最多的是任务扰动，识别此类扰动并量化是对其进行管理的基础工作.

1 任务扰动的识别

任务扰动是指工程项目中使实际情况与原计划不符合的各类干扰事件，其在实施过程中最终将导致工期和费用实际值与计划值的偏差.任务扰动对项目的影响，在业主方面主要表现为业主对项目完成的满意度，涉及项目工期、工程质量、工程成本等目标，尤为关注工程成本这一目标，因此主要分析任务扰动对业主成本满意度的影响；在承包商方面，主要表现为项目工期、项目施工成本等目标.

1.1 业主成本满意度扰动

业主满意度指业主对其明示的、通常隐含的或必须履行的需求或期望已被满足程度的感受，是对承包商的建筑产品或者服务的评价.每一个业主都希望承包商的建筑产品质量优、工期短、成本低并且其服务态度好[4].对此，业主有一个期望值，项目实际情况与业主的期望值偏差越小，则业主的满意度越高；反之，则满意度越低.考虑工程实际，研究业主对工程成本偏差的满意度以简化工作.

业主与承包商在合同中约定成本变动幅度后，即产生了可接受的最低成本和最高成本.通常业主都允许工程成本有一定的偏差，只要偏差在容许范围之内，则业主的满意度不受影响；否则可给予承包商一定惩罚.为使业主成本满意度不受影响或影响最小，成本偏差必须在业主的容许范围之内.

1.2 项目工期扰动

工程项目在实施前都会制定进度计划；当受到干扰后，其实际进度与计划进度会存在偏差；这种偏差将影响项目是否能够按原计划进行，因而需要对原进度计划进行调整.干扰管理就是将项目进度调整后的新方案与原方案相比，确保项目工期偏差最小，以期项目继续顺利进行.

1.3 项目扰动成本

当项目受到干扰时，为了减小扰动影响，需要采取相应措施；这将产生一定的成本，包括工期扰动成本、资源扰动成本、执行模式扰动成本等.工期扰动成本，是在工期扰动出现后，采用增加资源投入的方式来进行调整所付出的成本[5]；资源扰动成本，是由于项目在执行过程中，对资源使用不合理或资源本身受到扰动时，采取新调度措施而产生的扰动成本；执行模式扰动成本，即项目受扰动后，需要重新选择执行模式，继而产生一定的成本[3].

2 任务扰动的度量

考虑如下项目对象：由 n项活动构成，活动i(i=1,2, …, n)以m模式执行，所有可执行模式集合为 M；合同中约定，成本最大偏差为±a%，超出偏差范围后业主最大容忍值为Δci，其奖励系数、惩罚系数分别为θ1、θ2，且θ1、θ2∈(0,1)；各项活动i的计划作业时间为Ti0，延期惩罚系数为λi；各项活动所需综合资源的单价为νi，活动i受到扰动时的综合资源变动量为δi.

2.1 业主成本满意度的度量

在对业主满意度进行量化时，可借鉴顾客满意度指数(Customer Satisfaction Index)[6].顾客满意度指数(CSI)是由设在密歇根大学商学院的美国国家质量研究中心和质量协会提出的一个经济类指数；CSI越大，则顾客满意度越高.要测量顾客满意度，需要考虑对隐变量(满意度影响因素)及其权重进行估量[7].模型具体如下

式中：Y为顾客满意的隐变量；kx为顾客满意隐变量的第k个测量变量；E{Y}为隐变量Y的期望值；min{Y}为隐变量 Y的最小值；max{Y}为隐变量 Y的最大值；kω为第k个测量变量的权重.

对工程成本偏差进行度量时，由于调整方案优选关注于“扰动最小化”的目标，采用将“业主成本满意度最大化”问题转化为“业主成本不满意度最小化”问题的处理，有利于保持建模过程中的目标一致性.

项目计划阶段，拟定各项活动i计划成本为0iC ；根据合同约定，成本最大偏差为±a%，则业主可接受的最低成本和最高成本分别为ilC=0iC (1-a%)、Cih= Ci0(1+a%)，据此可建立活动i的业主成本不满意度目标函数ηi：

式中：ic为活动i的实际成本；icΔ为活动i的业主成本最大容忍值；如果第i个活动以m模式执行，xim=1，否则，xim=0.

进一步，可得项目的业主成本不满意度目标函数 ()U x

2.2 项目工期扰动的度量

干扰发生时，调整后方案与原计划方案活动 i的持续时间会存在差异.扰动管理的目标，是要使调整前后方案间的工期差异最小，以确保新调度方案对工程项目工期影响最小.据此建立工期偏差目标函数 ()T x

2.3 项目扰动成本的度量

项目扰动成本包括工期扰动成本、资源扰动成本和执行模式成本.对于工期扰动成本，如果活动i在新调度方案中的持续时间比原计划方案中的长，将产生惩罚成本，可采用工期偏差乘以惩罚系数来表示；反之，业主可对承包商进行适当奖励，考虑实际可略去不计.对于资源扰动成本，度量时可将其简化为活动i综合资源的单价iν乘以受扰动综合资源的变动量iδ.对于执行模式扰动成本的度量，即为所选用的新模式成本.据此，可分别建立目标函数工期扰动成本1()F x、资源扰动成本2()F x、执行模式扰动成本3()F x

据此可得项目扰动成本 ()F x为

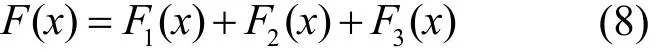
2.4 综合扰动度量

由于业主成本不满意度、项目工期扰动、扰动成本等三个目标值，具有不同的单位；因此在进行综合度量时，需进行无量纲化处理，即用数值大小来体现原始指标的优劣[8].

采用“Min-Max标准化”法来进行上述目标值无量纲化处理，是将属性 A的原始数据AiX 通过Min-Max标准化映射为区间[0，1]中的新数据AiX ，计算公式为

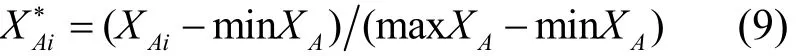
式中：minXA、maxXA为属性A的最小值和最大值.

计算项目的业主成本不满意度、工期扰动、扰动成本等三个目标值的平均值，将其作为一个原始数据，并找出构成每个目标值各分项值中的最大值、最小值代入公式(9)，即可得到对应的无量纲新数值.具体处理方式如下：

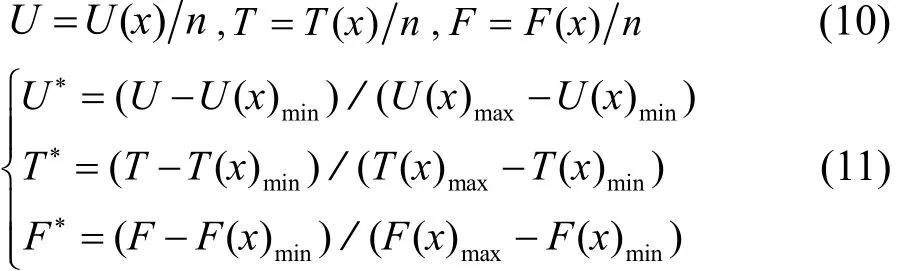
项目执行过程中发生干扰时，由于对业主成本不满意度、项目工期扰动、扰动成本等三个目标各有侧重，可通过对其设定不同权重系数1Z、2Z、3Z(1Z+2Z+3Z=1)来予以反映，据此得到调整方案的综合扰动度量值Z，即：

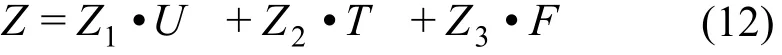
针对干扰发生后提出的所有可行调整方案，综合扰动值Z最小的方案，既保证了业主成本不满意度最小，又能兼顾项目工期偏差扰动和扰动成本，应作为最优方案予以采纳并实施.

3 算例

某项目共包含9项活动a、b、c、d、e、f、g、h、i，网络计划见图1所示.图中箭线上方注写值为活动代号；箭线下方注写的第一个数值表示该活动的持续时间，第二个数值表示该活动所需的综合资源量；经网络计算知，该项目关键线路是○1→○2→○3→○8→○9→⑩，工期为21 d；项目中各项活动的执行模式、持续时间、资源需求量、成本等信息见表1所示.

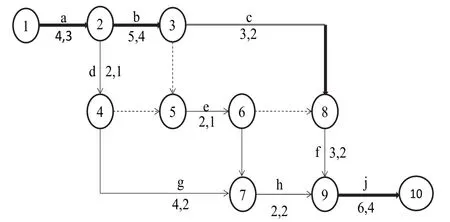
图1 项目网络图Fig.1 The project network

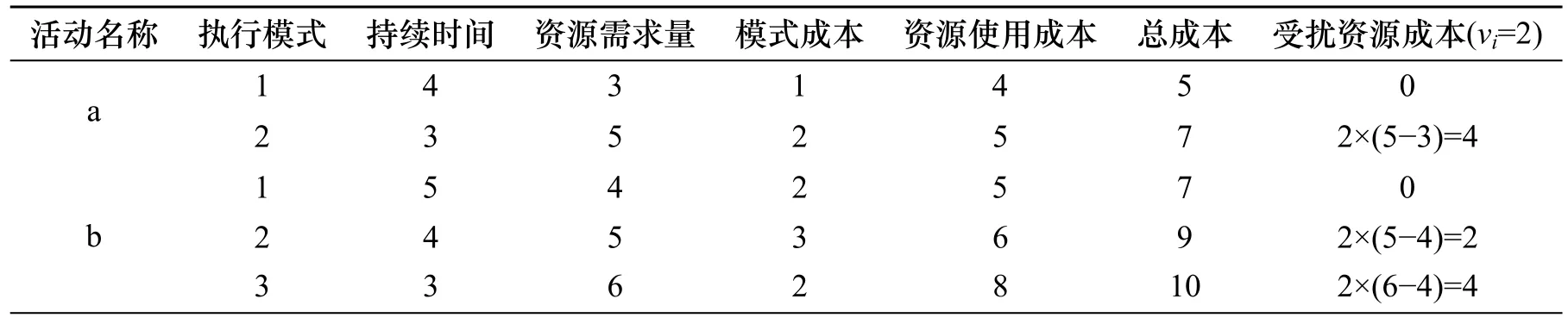
表1 项目活动的执行模式、持续时间、资源需求、成本等信息表Tab.1 Activity execution mode, duration, resou rce requirements and cost information

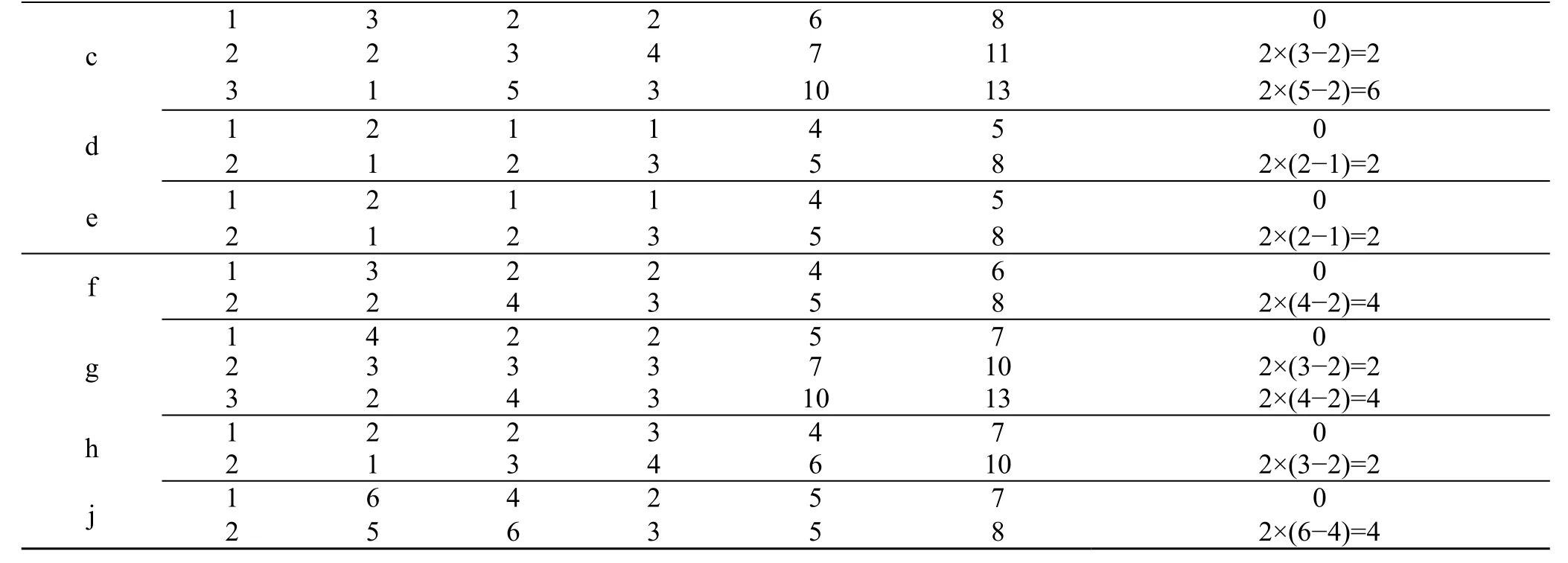
续表

考虑如下情景：原计划方案在执行到活动b时受到干扰，活动b由于受到干扰导致作业时间由5 d延长为7 d；由于活动b为关键工作，导致项目总工期将变为23 d.该扰动如果不进行调整，将引起后续工作的延迟、且造成资源扰动.

针对该项扰动，在制定新调整方案时，首先考虑关键工作；设定原进度方案中各工作执行模式默认为模式1.

为了说明模型计算过程，综合考虑分析后本文选取了如下4种备选调整方案，总工期均为21 d.各活动的新执行模式见表2所示，未调整的仍为模式1(由于活动a和b现已完成,故不予考虑) 按照上述4种调度方案，根据已建立的扰动模型计算其综合扰动值.根据公式(5)，本例iλ统一取值为2，则根据上文计算出的工期扰动偏差，计算出4个方案的工期扰动成本依次为1()F x =4、2()F x =4、3()F x =10、4()F x =4.

受扰资源成本2()F x度量，根据公式(6)，计算这里不再赘述；执行模式扰动成本3()F x度量，根据公式(7)，新方案各活动的执行模式成本在表1中已给出，亦不再赘述.

将扰动成本1()F x、2()F x、3()F x的结果进行汇总，计算综合扰动成本 ()F x，结果见表4.

(4)综合扰动度量：计算出业主成本不满意度、项目工期偏差扰动、扰动成本后，根据公式(10)、(11)进行无量纲化处理，最后根据公式(12)计算各方案的综合扰动值.本例中取 3个目标权重为：1Z=0.35，2Z=0.25，3Z=0.4，计算结果见表5.

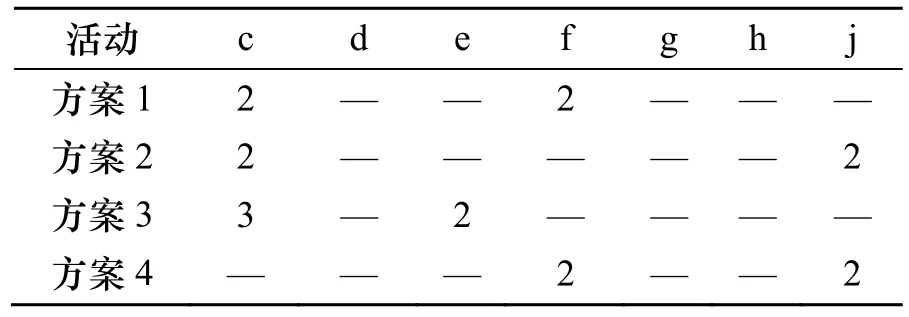
表2 新方案的各活动执行模式Tab.2 Activity execution mode of new program

(1)业主成本不满意度：约定成本允许偏差的幅度±a%，本例取±30%，则业主可接受的最低成本和最高成本分别为 Cil= Ci0(1-30%)、 Cih= Ci0(1+30%)，Δci统一设定为1；另外，本例取θ1=0.3、θ2=0.5，根据公式(2)，业主成本不满意度ηi的计算结果见表3.

(2)工期扰动偏差度量：根据公式(4)，将调整前后方案中各活动的持续时间进行比较计算，得到 4个方案的工期扰动偏差依次为 T ( x)1=2、 T ( x)2=2、T( x )3=5、 T ( x)4=2.

(3)扰动成本的度量：工期扰动成本 F1( x)度量，

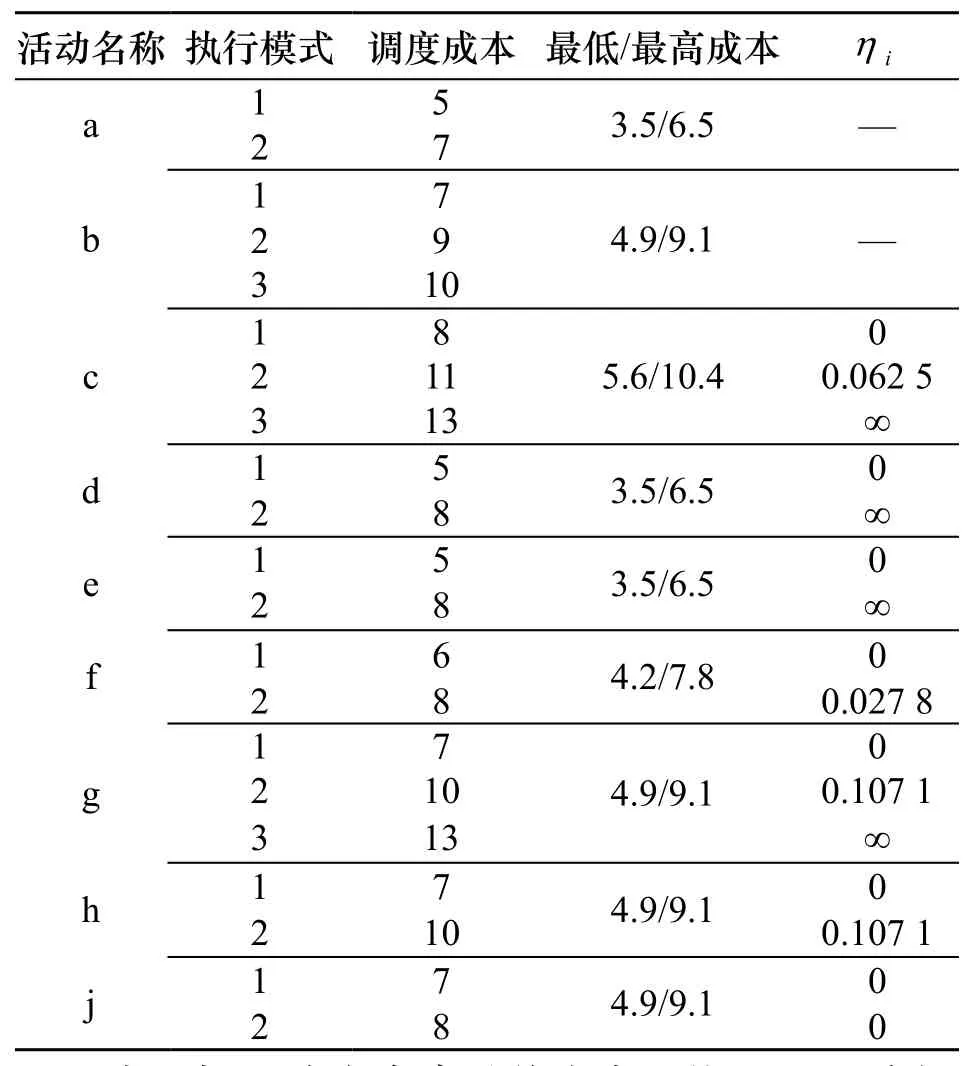
表3 业主成本不满意度计算表Tab.3 Calculation results of owner dissatisfaction of cost

对比表 5中各方案的综合度量值，可以看出，方案2对系统扰动最小；方案4较之方案2，虽然业主成本不满意度较小，但扰动成本较高；方案 1较之方案2，业主成本不满意度偏高；方案3由于业主成本不满意度为∞，且扰动成本较高，故应予淘汰.因此，应选中方案2作为新的调整方案予以实施.

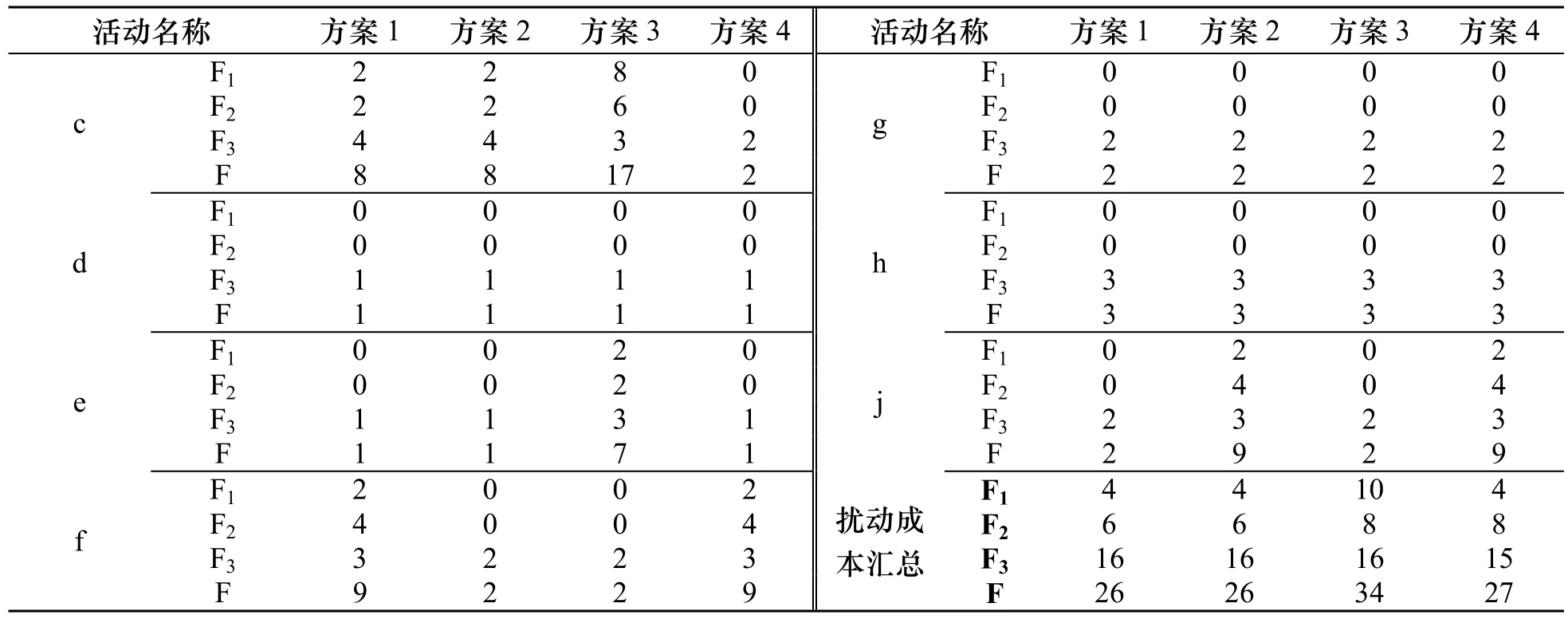
表4 扰动成本汇总表Tab.4 Summary of disturbance cost

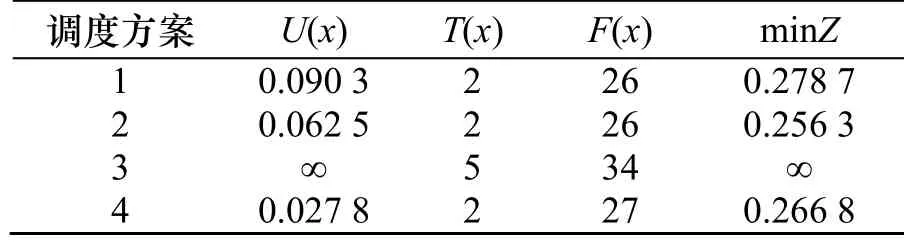
表5 各方案的结果对比Tab.5 The comparison between results of each scheme

4 结语

以项目实施中常见的任务扰动为研究对象，从干扰管理视角对其进行了分析，采用主观性的业主成本不满意度衡量方法与客观性的工期扰动、扰动成本衡量方法相结合的思路，比较全面地描述了任务扰动对项目执行的影响；文中建立的任务扰动综合度量方法，在干扰发生后项目调整方案的优选中，能综合考虑扰动对成本、工期的影响，并突出强调了“扰动最小”的原则，可保证能够以最小偏差使项目继续执行下去；及时并准确进行任务扰动管理是干扰管理实践的重要工作，未来可进一步开展关于项目工期和工程质量的业主满意度相关研究.

References

[1] Y Gang, Q Xiangtong. Disruption management:framework, models and applications[M]. Singapore:World Scientific Publishing Co.Pte.Ltd, 2004.

[2] ZHU G, BARD J F, YU G. Disruption management for resource-constrained project scheduling[J].Journal of the Operational Research Society,2005,56(4):365-381.

[3] 刘志霞.资源受限项目调度问题及其任务扰动的干扰管理研究[D]. 沈阳: 沈阳工业大学, 2011:40-51.LIU Zhixia. Research on the resource-constrained project scheduling problem and disruption management for activity disruption [D]. Shenyang:Shenyang University of Technology, 2011:40-51.

[4] 朱宾梅, 刘晓君, 王智辉. 基于精益建造下工程项目质量、成本、工期三要素管理的新思维[J].建筑经济.2007, (11): 13-15.ZHU Binmei, LIU Xiaojun, WANG Zhihui. New management thinking of the three elements of project quality, cost and time limit based on lean construction[J]. Construction Economy. 2007,(11): 13-15.

[5] 乌日娜, 徐方舟, 陆惠民. 项目资源约束下工期最短-资源均衡优化算法[J].项目管理技术. 2013,11(7):103-107.WU rina, XU fangzhou, LU huimin. Under the project resource constrained shortest duration-resource leveling optimization algorithm[J]. Project Management Technology. 2013,11(7): 103-107.

[6] 杨耀红, 张俊华, 曹继辉.工程项目建设监理的业主满意度分析[J].华北水利水电学院学报.2003,24(2):70-71.YANG Yaohong, ZHANG Junhua, CAO Jihui.Analysis on employer satisfaction with construction supervision for engineering project[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power. 2003,24(2): 70-71.

[7] 梁燕.关于顾客满意度指数的若干问题研究[J]. 统计研究.2003, 11(11): 52-56.LIANG Yan. Research on several problems about the customer satisfaction index[J]. Statistical Research.2003, 11(11): 52-56.

[8] 郭亚军, 易平涛. 线性无量纲化方法的性质分析[J].统计研究.2008,25(2): 93-100.GUO Yajun, YI Pingtao. Character analysis of linear dimensionless methods[J].Statistical Research. 2008,25(2): 93-100.