在ABAQUS中开 发实现Mortara界面循环本构模型

任 宇，陈仁朋，陈云敏

(1.中国电力工程顾问集团华东电力设计院，上海 200063; 2. 浙江大学建筑工程学院，浙江 杭州 310058)

ABAQUS由美国的HKS公司研制开发，是目前世界公认的最为先进的大型通用非线性有限元分析软件，在几何、材料非线性和复杂接触问题等方面的分析能力居世界领先水平，特别适用于岩土工程这种包含高度材料非线性及复杂界面接触问题的求解．

在岩土工程数值分析中，结构-土界面特性的模拟一直是其中的重点及难点．特别对于桩、锚杆和土钉等这些主要通过界面将荷载传递至周围土中的土工结构来说，界面的力学特性往往决定了整个土工结构的承载及变形性状[1]．

ABAQUS中自带的界面模型包括切向摩擦模型和法向接触模型两类，其中摩擦模型用以模拟接触面间的剪应力传递规律，一般为库伦摩擦模型；法向接触模型则用来模拟接触面间法向应力传递规律，包括“硬接触”（hard contact）和“软接触”(softened contact)两种模型[2]．目前ABAQUS中的界面模型在使用时是相互独立的，较少考虑了切向和法向间的耦合作用，如现有界面模型中就没有考虑剪切作用对于法向应力-应变关系的影响等．然而这与界面剪切试验中所观察到的现象并不吻合：剪切通常会引起界面土体体积的改变，进而会影响到法向应力的大小[1-3]．更为重要的是，现有模型仅是针对于静载下的界面性状的，软件中还没有能够用于模拟界面循环加载性状的本构模型．这一缺憾无疑极大限制了 ABAQUS在土工结构循环加载性状数值分析中的应用范围．

为了弥补自带界面模型的不足，ABAQUS基于其子程序扩展平台，提供了允许用户自定义所需界面特性的用户界面子程序UINTER(User subroutine to define surface interaction behavior for contact surfaces)．UINTER 能够让用户定义并使用ABAQUS中所没有的界面本构模型．这一功能极大地拓展了软件在土与结构相互作用分析中的应用范围．

基于ABAQUS提供的UINTER子程序，完成了 Mortara界面循环模型(Mortara cyclic interface model)的开发工作．对界面循环剪切试验进行了建模分析，将 ABAQUS有限元分析结果与文献给出的数值解结果进行了对比．结果表明，UINTER的求解效率和精度令人满意，有望成为 ABAQUS中模拟结构-土界面循环加载性状的强有力分析工具．

1 Mortara界面循环模型

1.1 Mortara界面循环模型

Ghionna 和 Mortara[4]基于经典弹塑性理论建立了一个模拟界面静载性状的二维弹塑性本构模型．模型的屈服面方程借鉴了Vermeer[5]的偏应力屈服面的概念，在 τ－σn空间内体现为是一条原点出发微弯的曲线．模型采用非关联流动法则，模型势函数则与传统剑桥模型的相类似．

与传统弹塑性模型类似，在上述界面静力模型中，卸载及再加载过程中的应力路径一直处于屈服面内，此时界面的应力-应变关系均表现为弹性，并不能反映出循环加载下界面土颗粒重排导致塑性变形累积的特征．为此，Mortara等[6]对上述界面静力本构模型进行了发展，在原有屈服面内引入了一个小的运动屈服面；当应力点落在运动屈服面内时，界面仅产生弹性变形，如若应力试图穿过运动屈服面，就会引发弹塑性变形，同时会拖移运动屈服面在外边界面内发生移动．该模型可以较好地表征出界面在卸载及再加载下的塑性变形产生过程．

1.2 本构模型的数学表达式

1.2.1 屈服函数

Mortara界面循环模型包含有外边界面和内部运动屈服面（简称内面）两个屈服面．模型的外边界面和内部屈服面的方程分别为

式中：α为硬化-软化参数，它的取值决定了外边界面的大小及位置；α0为移动屈服面的边线与中心轴线间的夹角；为以局部参考坐标系中的应力值，该坐标是将原坐标的τ=0轴旋转θ得到的．

图1 界面循环模型的屈服面Fig. 1 Yield surfaces of the interface model

1.2.2 映射法则

当应力点在边界面内移动时，需要建立映射法则来确定塑性模量随屈服面移动的变化情况． 外边界面内的塑性模量由下式计算：

上式与 Dafalias和 Popov[7]所提出的映射函数形式相类似．其中:rθ为内外屈服面对应边界线间的角度；0rθ则为应力路径发生折返穿过弹性区再次达到内屈服面上时的rθ．Hα为加载至外边界面时所对应的塑性模量．h则由下式计算

式中: n和hχ为模型参数；0s为一任意参考位移，用于将hχ无量纲化；max[]p u 为最大法向累积塑性变形；inh 则由下式计算

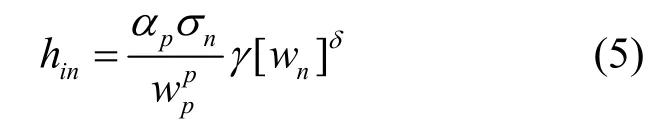
其中，γ和δ为模型参数．式(4)中Rαθ则由下式定义

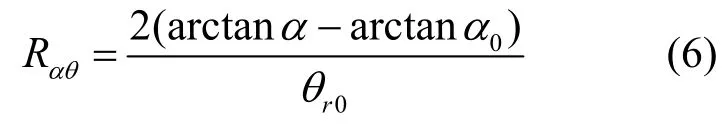
1.2.3 循环流动法则

界面模型在第i周循环下流动法通过下式表示

式中：η为应力比，η =τ/ σn；d为剪胀率．可以看出，模型采用的流动法则在η−d平面内表现为线性，为第i周循环中流动法则在η轴上的截距．模型中通过与法向塑性累积变形的关系来考虑循环对于流动法则的影响

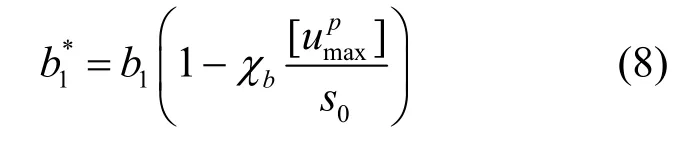
式中：bχ为模型参数．

Mortara界面循环模型是一种高度非线性的界面弹塑性模型，能够较为精确地对循环加载下结构-土界面的复杂力学行为进行描述，特别是能够很好地对循环下界面土体的剪缩性状进行模拟．该模型是一个非常有应用价值和发展前途的岩土本构模型．

2 界面子程序开发

2.1 UINTER子程序

为了方便及鼓励用户自行定义符合特定问题的模型及单元，ABAQUS提供了大量的用户自定义子程序（user subroutine），UINTER是其中支持用户自定义界面特性的子程序．UINTER功能非常强大，不但可用于定义接触面间的力学行为，也可对界面间的热力学性状进行定义．用户可以将所需的界面本构关系编写入UINTER，并在有限元分析中进行调用．

ABAQUS默认采用Newton-Raphson迭代法求解非线性方程组，当每一个增量步开始时，ABAQUS主程序都会在界面每个积分点上调用UINTER，传入当前状态应力、应变及状态变量等相关参数；UINTER则根据传入参数，求解出主程序给出应变增量下所相应的应力增量，并更新应力及相关其他参数，并向主程序提高更新后的雅克比矩阵；主程序根据应力增量计算出残余荷载，并根据残余荷载求得相应误差，如果不满足指定误差条件，ABAQUS将进行迭代，直至达到收敛准则，然后进入下一增量步的计算[2]．

2.2 带误差控制的显式积分算法

Newton-Raphson法中的关键步骤是确定每次迭代中的残余荷载，为此必须计算本次迭代结束时的总应力．通过对本构方程积分得到应力增量的方法叫做应力积分法，包括显式积分算法和隐式积分算法两种．

传统显式欧拉积分法的计算精度较低，预测应力往往会偏离实际屈服面，易于产生屈服面漂移．Potts等[8]提出了旨在消除屈服面偏移的修正算法，极大地提高了显示积分算法的精度．Potts等[9]将带误差控制的显式欧拉积分算法与隐式积分法进行了比较，指出两种算法均能得到令人满意的积分结果，但是相较于隐式算法，显式算法对于复杂本构模型的适用性更好．对于一些复杂的本构模型，往往难以推导出适合于隐式回归计算的公式．因此，本文选取 Potts等提出的带误差控制的修正欧拉显式积分法对本构方程进行积分计算．

显式积分计算步骤主要包括两步：①弹性预测；②弹塑性应变积分．弹性预测过程中假设变形增量为纯弹性，按照弹性本构关系计算相应的应力增量，如果增量结束时的应力仍在屈服面内，则说明弹性预测得到的应力增量是准确的；如果超过屈服面，则说明应变不全是弹性的，应该对弹塑性部分进行积分以获得正确的应力增量．由于循环模型中存在内外两个屈服面，包含了两种势函数及硬化法则，因此还需要判断显式积分过程中的应力状态是否超过了外边界面，如果超过则需要采用外边界面所对应的势函数及硬化法则计算相应的弹塑性方程矩阵．

每个次阶计算结束时，需要对应力及硬化参数计算结果进行检查，判断其是否满足屈服准则，如果不满足即可以转入屈服面偏移修正计算流程中，只有满足了屈服准则后才转入下一次阶计算流程．详细的积分步骤在文献[10]中给出．

2.3 子程序结构

基于本构模型公式和应力积分算法，参照ABAQUS用户界面子程序的接口规范，进行了UINTER的程序设计及代码编写．代码由 Fortran语言编写．图2中给UINTER的计算流程．文献[10]中给出了具体的程序代码．

图2.UINTER计算流程图Fig 2. Flow chart for UINTER calculation

3 数值验证

为了对所开发的UINTER子程序进行验证，笔者将自定义 UINTER程序接入 ABAQUS/Standard中，对界面循环剪切试验进行了数值模拟，并将计算结果与文献[6]提供数值计算结果进行了对比．用于验证的有限元模型如图3所示．模型由两部分组成，一个尺寸为1.0 m×1.0 m×1.0 m的三维弹性正方体，压在一尺寸为3.0 m×3.0 m×1.0 m的刚体上．弹性体与刚体间设置接触面对，接触面间力学特性由自定义UINTER子程序定义．弹性体划分为1个单元，刚体划分为9个单元．弹性体的弹性模量设为10GPa．为保证剪切过程中弹性体水平方向的尺寸保持恒定，弹性体的泊松比ν=0．

图3.界面循环剪切试验有限元分析模型Fig. 3 FE model for cyclic interface shear test

Mortara界面循环模型的计算参数取自文献[6]，见表1．在所对应界面循环剪切试验中，试验土体为Toyouta砂，界面为铝板，粗糙度为30 μm，相对密实度DR=85%，法向初始应力0nδ=150 kPa．分析中选取常法向刚度条件下的剪切试验进行分析，法向刚度K=500 kPa/mm，w△=0.8mm，[wmean]=0.4 mm．计算开始时首先在弹性体的法向施加初始法向应力0nδ，剪切过程采用位移控制方式施加，对弹性体施加水平x向的位移，以模拟土与结构间的剪切过程．

表1.算例的Mortara模型参数Tab. 1 Parameters of the model

数值计算与解析解计算结果对比情况如图 4-6所示．图 4-6中分别给出了循环剪切下的剪应力 τ与剪切位移w、法向应力σn与剪切位移w、剪应力τ与法向应力σn间的变化规律．从图中可以看出，本文数值模拟结果与文献解析解间有着很好的一致性，验证了本子程序对界面循环加载性状的模拟能力，说明本文UINTER成功实现了Mortara界面循环模型的开发．

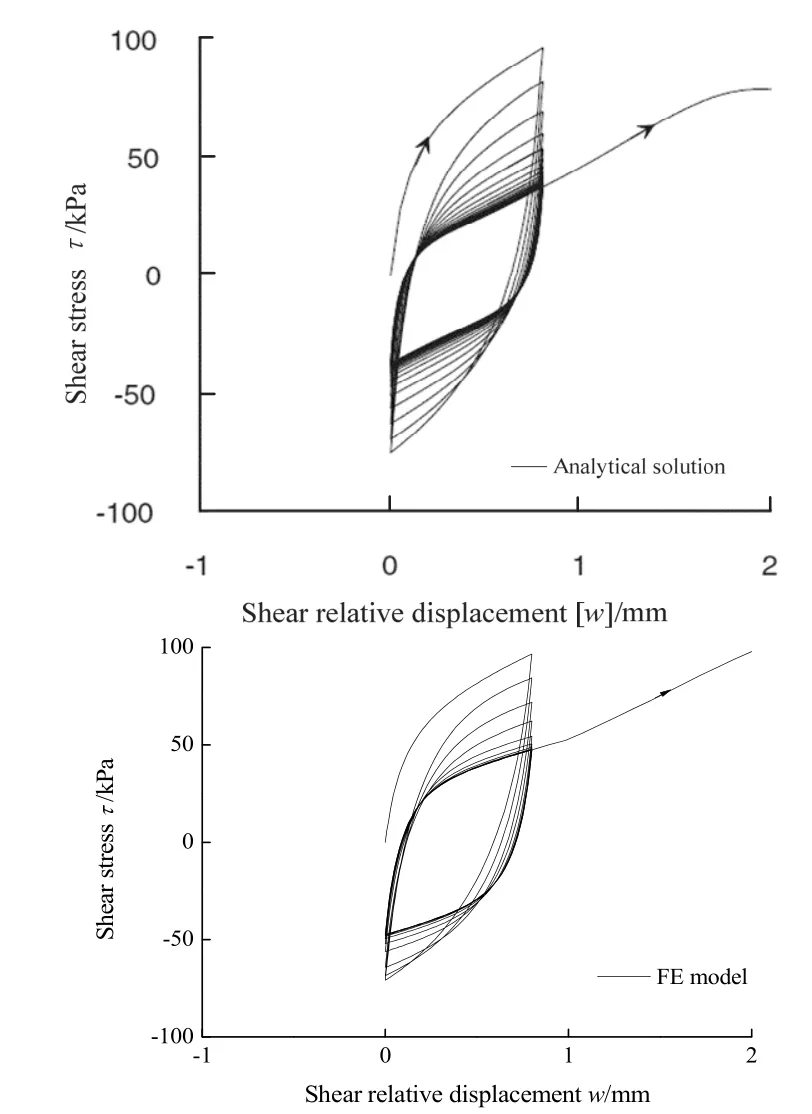
图4.循环剪切试验中～wτ关系的解析解与数值解对比Fig. 4 Comparison between relationships of ～wτ obtained from analytical and numerical solution

图5.循环剪切试验中 σ n ～ w关系的解析解与数值解对比Fig. 5 Comparison between relationships of σ n ～w obtained from analytical and numerical solution

从图4及图5中的模拟结果可以清晰看出，循环剪切下的界面将会产生明显的滞回特性，同时循环剪切下的界面土体会随循环产生剪缩，由此导致界面法向减小，剪应力弱化．随着循环次数的增加，剪应力及法向应力会逐渐趋于稳定，并在τ～σn呈现出典型的“蝶型”变化规律（图6）．这些与界面循环剪切试验中所观测到的现象是一致的．这不但证明了Mortara界面循环模型对于复杂循环特性的精确描述能力，也验证了本子程序运算的正确性．

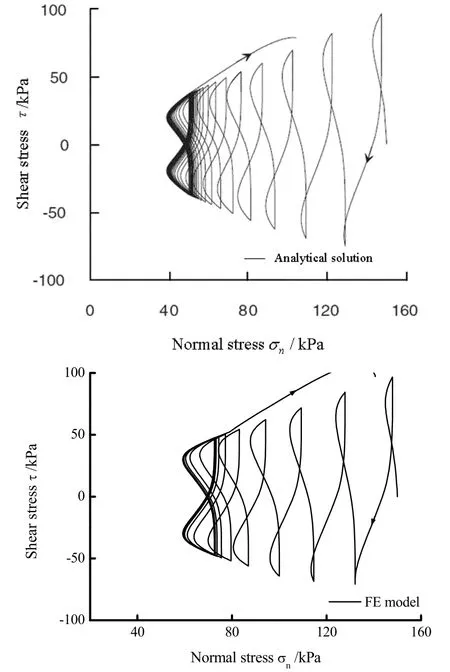
图6.循环剪切试验中 τ ～ σ n关系的解析解与数值解对比Fig. 6 Comparison between relationships of τ～σn obtained from analytical and numerical solution

4 结 语

Mortara界面循环模型是一个优秀的界面本构模型，能够很好地对循环荷载作用下土-结构界面复杂的力学特性进行描述，包括应力-应变滞回特性、法向体积剪缩、剪切强度弱化等．通过本文研究，得到以下结论：

基于ABAQUS用户子程序开发平台UINTER，实现了对Mortara界面循环模型的二次开发．算例结果显示，自开发的UINTER子程序具有很好的运算稳定性及精度，能够模拟出土-结构界面的循环加载性状．

利用 ABAQUS强大的非线性有限求解能力及优秀的前后处理界面，结合本文所开发的 Mortara界面循环模型的UINTER子程序，有望实现对循环荷载作用下土与结构相互作用问题数值分析．

子程序的成功开发极大扩展了该界面本构模型在岩土研究及设计中的应用，同时也为其他界面本构模型在ABAQUS中的开发提供了借鉴和参考．

References

[1] MORTARA G, MANGIOLA A, GHIONNA V N. Cyclic shear stress degradation and post-cyclic behavior from sand -steel interface direct shear tests[J]. Canadian Geotechnical Engineeing Journal, 2007, 44(7): 739-752.

[2] ABAQUS user’s and theory manuals[M]. Rhode Island,Hibbitt: Karlsson & Sorensen Inc., 2004.

[3] FAKHARIAN K, EVGIN E. Cyclic simple-shear behaviour of sand-steel interfaces under constant normal stiffness condition[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1997, 123(12):1096-1105.

[4] GHIONNA V N, MORTARA G. An elastoplastic model for sand-structure interface behavior[J]. Géotechnique,2002, 52(1): 41-50.

[5] VERMEER P A. A double hardening model for sand[J].Géotechnique, 1978, 28(4): 413-433.

[6] MORTARA G, BOULON M, GHIONNA V N. A 2-D constitutive model for cyclic interface behavior[J].International Journal for Numerical Analytical Methods in Geomechanics, 2002, 26(11): 1071-1096.

[7] DAFALIAS Y F, POPOV E P. Plastic internal variables formalism of cyclic plasticity[J]. ASME, Journal of Applied Mechanics, 1976, 43(4): 645-651.

[8] POTTS D M, GENS A. A critical assessment of methods of correcting for drift from yield surface in elasto-plastic finite element analysis[J]. International Journal for Numerical and Analytical Method in Geomechanics,1985, 9: 149-159.

[9] POTTS D M, GANENDRA D. An evaluation of substepping and implicit stress point algorithms[J].Computer Method In Applied Mechanics Engineering,1994, 119(3/4): 341-354.

[10] 任宇. 长期竖向循环荷载作用下桩的累积变形特性试验及理论研究[D]. 杭州: 浙江大学, 2013.REN Yu. Model test and theoretical study on the long-term deformation of single pile to cyclic axial loading [D]. Hangzhou: Zhejiang University, 2013.