高层建筑斜交网格筒结构侧向位移角研究

史庆轩，任 浩，戎 翀，桑 丹

（西安建筑科技大学土木工程学院，陕西 西安 710055）

斜交网格筒结构体系是一种新型的结构体系，具有抗侧刚度大的优点[1-3]，目前该类型结构体系已在国内外有多例成功实践[4-5]．在我国斜交网格筒结构多处在抗震设防烈度较低的区域．作为一种新型结构体系，与常规的结构体系相比，外筒结构形式、传力路径、受力机理等存在较大差异[6]．该结构体系的工程经验超前于理论研究．掌握该结构的基本力学性能是将其应用于设防烈度较高区域的前提．

目前该新型结构体系既没有经受过大震检验，也没有丰富的工程经验，国内外对其力学性能的研究较少[7]，斜交网格筒结构在多遇地震作用下的弹性位移角限值也没有明确的规定．建立斜交网格筒结构变形转角的计算方法，探讨斜交网格筒结构的弹性位移角限值，分析斜交网格筒结构在侧向荷载作用下子模块的变形转角和角部斜柱轴向应变之间的关系，对确保该结构体系的抗震设防，以及进行合理抗震设计具有重要意义．

本文推导了斜交网格筒结构子模块的侧向刚度的简化计算式．通过子模块的剪切刚度和弯曲刚度的简化计算式得出了结构子模块的剪切转角和弯曲转角的计算式．通过结构角部斜柱的轴向应变与子模块变形转角之间的关系，建立了子模块变形转角的计算方法，并通过SAP2000软件进行了验证．提出根据斜交网格筒结构各子模块的变形转角，来控制结构在弹性阶段时的侧向刚度及变形能力．建议根据结构具体的几何参数，不同斜柱角度的结构应采取不同的弹性位移角限值．

1 侧向刚度的简化计算

1.1 子模块剪切刚度的简化计算式

高层斜交网格筒结构子模块的腹板由n(n为主环梁跨数)个交叉斜柱单元组成，交叉单元如图1所示，在剪力作用下，腹板平面每个交叉单元沿水平方向上的顶点位移是相同的．所以，首先推导出一个交叉单元的抗剪刚度，然后乘以主环梁跨数n即为子模块腹板的抗剪刚度．

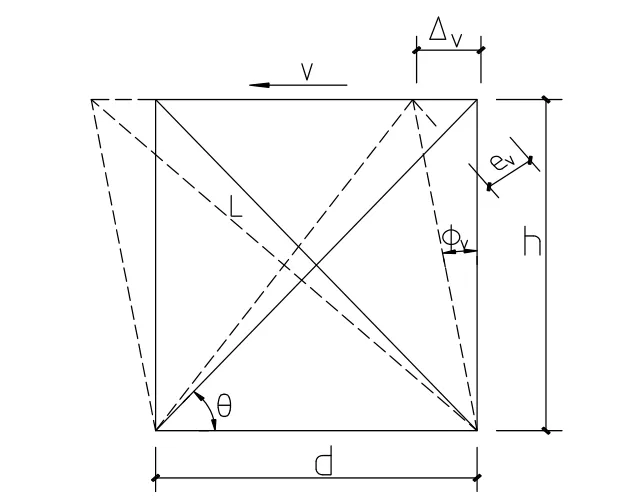
图1 交叉斜柱单元变形简图Fig.1 Cross diagonal column element deformation diagram

子模块所受的剪力和斜柱轴力之间的关系为

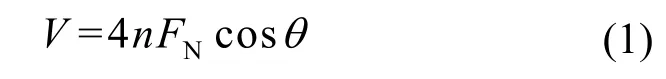
式中：V是子模块承受的剪力；FN是腹板斜柱的轴力；n是主环梁跨数；θ是斜柱和水平方向的夹角．

腹板斜柱轴力和斜柱应变之间的关系为

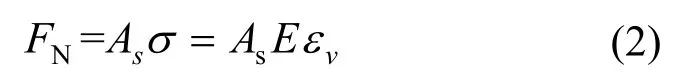
式中：As是斜柱的横截面积；σ是腹板斜柱的应力；εv是腹板斜柱的应变；E是斜柱材料的弹性模量．

在剪力作用下，子模块的剪切变形和腹板斜柱应变之间的关系如下式所示：

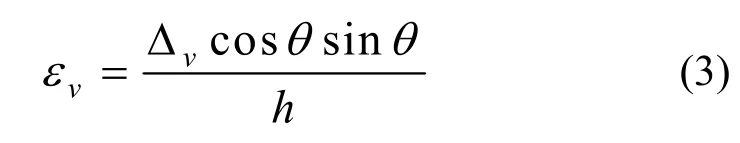
式中：△v是剪力作用下子模块的剪切变形；h为子模块的高度．

由式(1)～(3)可得子模块的剪力和剪切转角之间的关系式为

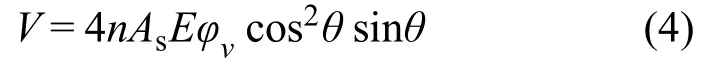
由式(4)可得子模块剪切刚度的计算式为

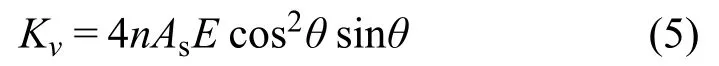
1.2 子模块弯曲刚度的简化计算式

子模块在弯矩M的作用下，主环梁上相交于同一节点的两根斜柱产生的轴向变形相等．离中轴线(在M作用下高度不发生变化的竖轴)越远，斜柱产生的轴向变形越大，且相交节点位于中轴线上的两根斜柱不产生轴向变形．本文以主环梁跨数n=6的斜交网格筒结构模型为例，推导子模块弯曲转角的简化计算式．子模块在弯矩M作用下腹板的变形图如图2所示.

假设在弯矩M作用下，子模块的端部产生的竖向位移为△M，腹板从边柱向中轴，主环梁上相交于同一节点的各斜柱产生的轴向变形依次为(上角标表示的是节点的编号，从两边向中间依次为1，2，3如图2所示)，则腹板的边柱产生的轴向变形为在弯矩M的作用下节点2产生的竖向位移为相交于节点2的两根斜柱的轴向变形为，节点3的竖向位移为13△M，相交于节点3的两根斜柱的轴向变形为

图2 在弯矩M下子模块腹板的变形图Fig.2 The deformation diagram of sub modules under bending

子模块在弯矩M作用下，斜柱轴力和斜柱应变之间的关系为

式中：As是斜柱的横截面积；iσ是斜柱应力；iε是弯矩M作用下斜柱的应变；E是斜柱材料的弹性模量．

在弯矩M作用下，斜柱的轴向变形和斜柱应变之间的关系如下式所示：

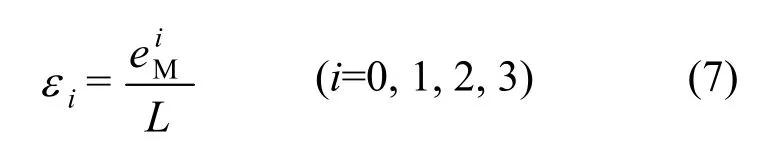
其中L为斜柱的长度.

由式(6)和(7)可得子模块在弯矩M作用下，斜柱的轴力和轴向变形之间的关系式：

子模块承受的弯矩M和斜柱轴力的关系式为

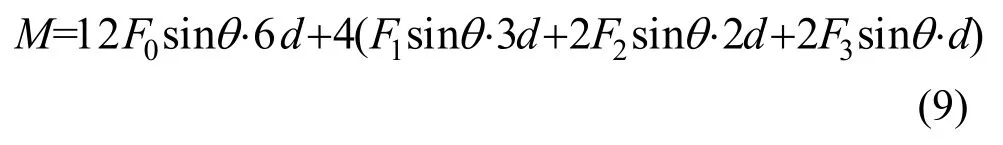
式中：F0表示翼缘斜柱的轴力F0=AsE△Msinθ/L；F1，F2，F3分别表示腹板相交于节点1，2，3的斜柱轴力，△Msinθ / 3L．

弯曲转角Mφ和子模块的端部产生的竖向位移△M之间的关系为

由式(9)和(10)可得子模块承受的弯矩M和弯曲转角之间的关系式为

由式(11)可得子模块的弯曲刚度的计算式为

由式(5)和(12)可以得出剪切刚度和弯曲刚度随斜柱角度的变化情况如图3所示，从图3中可以得出，剪切刚度和弯曲刚度均随着斜柱角度的增大而减小，剪切刚度受斜柱角度的影响更加明显．结构的侧向刚度由剪切刚度和弯曲刚度组成，由此可以推断出斜交网格筒结构的侧向刚度随着斜柱角度的增大而减小．

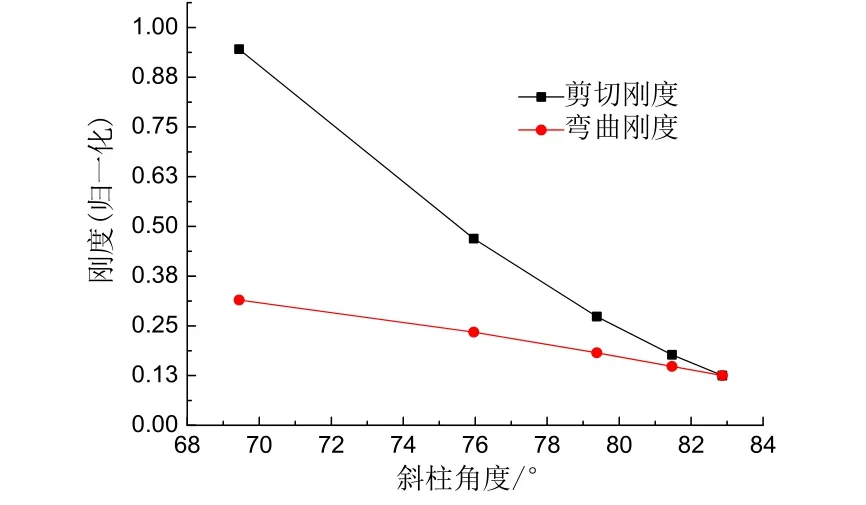
图3 剪切刚度和弯曲刚度随斜柱角度的变化Fig.3 Shear stiffness and bending stiffness variation with the angle of the inclined column

2 变形转角的计算

2.1 计算方法

斜交网格筒结构在侧向荷载作用下子模块的变形转角由剪切转角和弯曲转角组成．由上节可知，斜交网格筒子模块上承受的剪力和弯矩对子模块的剪切转角和弯曲转角的大小有影响，而结构的侧向荷载的分布形式决定了结构子模块上所承受的剪力和弯矩的大小．所以，斜交网格筒结构的侧向荷载的分布形式，对子模块的剪切转角和弯曲转角的大小有明显的影响．对于高层建筑结构而言，一般有三种典型的侧向荷载分布形式，其中包括顶点集中荷载、侧向均布荷载和侧向倒三角形分布荷载．斜交网格筒结构在三种不同的侧向荷载作用下，将结构承受的侧向荷载简化为结构子模块上的弯矩M和剪力V，利用上节推导出来的公式便可得出剪切转角和弯曲转角的大小以及它们之间的比例关系．

2.2 计算模型

参考国内外已有的工程实例，建立不同斜柱角度的斜交网格筒结构模型．所有的模型层高均为4 m，共32层，结构平面尺寸为36 m×36 m；各模型主环梁跨数均为6跨．斜柱和斜柱以及斜柱和环梁均采用刚性连接．各模型立面如图4所示．斜交网格筒结构的斜柱均采用圆钢管，并且以子模块为单位调整截面尺寸，材料均采用Q345．环梁均采用工字型钢400 mm×300 mm×10 mm×16 mm．在用钢量相等的原则下建立不同斜柱角度的斜交网格筒结构模型各模型均满足强度和稳定性要求．

图4 不同斜柱角度的斜交网格筒模型立面Fig.4 The elevation chart of diagrid tube

2.3 剪切转角的计算

由式(4)可得剪切转角的计算式为

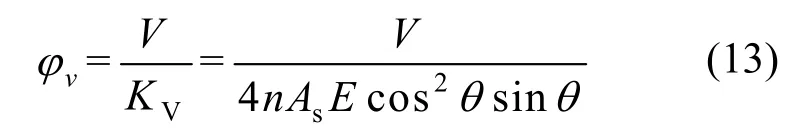
斜交网格筒结构在三种不同的侧向荷载作用下，将结构承受的侧向荷载简化为结构底部子模块上的剪力V．将不同斜柱角度的斜交网格筒结构模型的几何参数以及底部子模块斜柱截面的参数代入式(13)中，得出斜交网格筒结构在三种不同的侧向荷载作用下的剪切转角随着斜柱角度的变化情况如图5所示．从图5中可以得出，在相同的侧向荷载作用下，随着斜柱角度的增大，剪切转角逐渐增大，其中顶点集中荷载作用下剪切转角增加的最快，侧向均布荷载作用下剪切转角增加的最慢．

图5 剪切转角随着斜柱角度的变化Fig.5 The change of shear angle with the angle of inclined column

2.4 弯曲转角的计算

由式(11)、(12)可得弯曲转角的计算式为

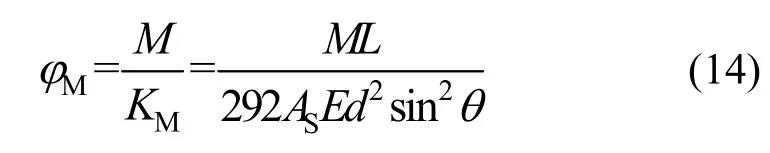
斜交网格筒结构在三种不同的侧向荷载作用下，将结构承受的侧向荷载简化为结构底部子模块上的弯矩M．将不同斜柱角度的斜交网格筒结构模型的几何参数以及底部子模块斜柱截面的参数代入式(14)中，得出斜交网格筒结构在三种不同的侧向荷载作用下的弯曲转角随着斜柱角度的变化情况如图6所示．

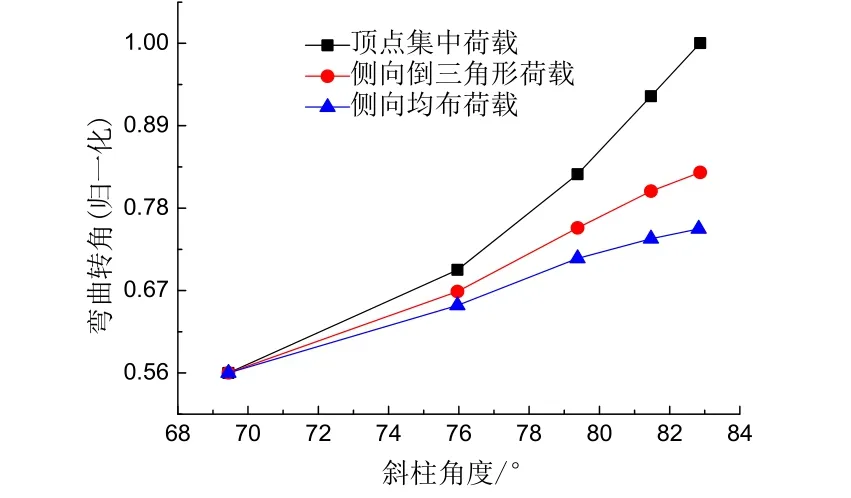
图6 弯曲转角随着斜柱角度的变化Fig.6 The change of bending angle with the angle of inclined column

从图6中可以得出，在相同的侧向荷载作用下，随着斜柱角度的增大，弯曲转角逐渐增大，其中顶点集中荷载作用下弯曲转角增加的最快，侧向均布荷载作用下弯曲转角增加的最慢．

2.5 剪切转角和弯曲转角之间的比值

由式(13)、(14)得剪切转角和弯曲转角比值的计算式为

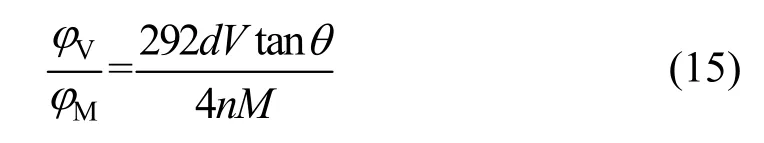
式中：n为主环梁跨数，d为主环梁跨长．

斜交网格筒结构在三种不同的侧向荷载作用下，将结构承受的侧向荷载简化为结构底部子模块上的弯矩M和剪力V．将不同斜柱角度的斜交网格筒结构模型的几何参数代入式(15)中，得出斜交网格筒结构在三种不同的侧向荷载作用下的剪切转角与弯曲转角的比值随着斜柱角度的变化情况如图7所示．

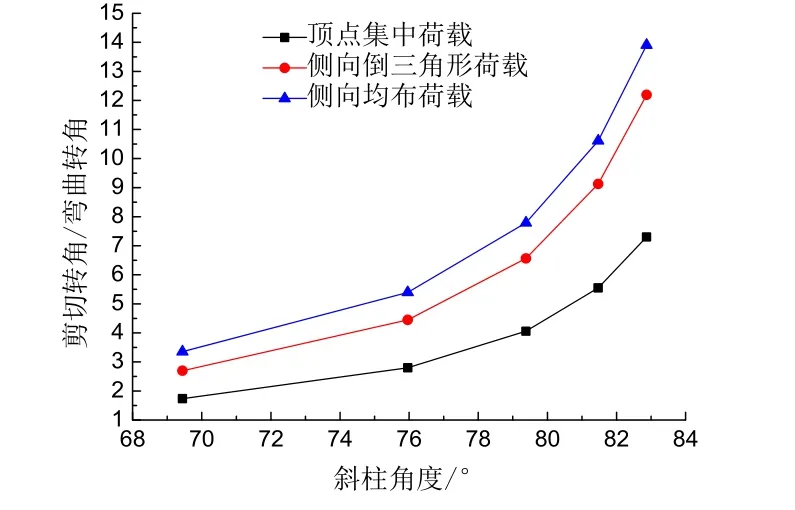
图7 剪切转角/弯曲转角随斜柱角度的变化Fig.7 The change of ratio of shear angle and bending angle with the angle of inclined column

从图7中可以得出，在相同的侧向荷载作用下，随着斜柱角度的增大，剪切转角与弯曲转角的比值逐渐增大．斜柱角度相同时，侧向均布荷载作用下剪切转角和弯曲转角的比值最大，顶点集中荷载作用下剪切转角和弯曲转角的比值最小．

2.6 变形转角的计算

斜交网格筒结构具有强大的抗侧刚度，斜柱作为其主要的抗侧力构件，在侧向荷载作用下主要表现为轴向的拉压屈服机制．已有研究表明，在侧向荷载作用下斜交网格筒结构的塑性铰首先出现在结构腹板角部的斜柱上[8]．本节基于结构腹板角部斜柱的轴向变形与子模块变形转角之间的关系来建立斜交网格筒结构子模块变形转角的计算式．其中变形转角由剪切转角和弯曲转角组成；斜柱的轴向变形分别是由子模块的剪切变形、弯曲变形和结构在竖向荷载作用下的变形引起的．

子模块变形转角与腹板角部斜柱的轴向应变之间的关系式为

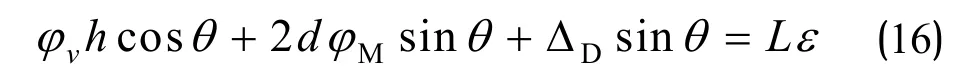
式中：斜交网格筒子模块剪切转角和子模块角部斜柱轴向应变之间的关系为φv=εv/cosθsinθ；弯曲转角和子模块角部斜柱轴向应变之间的关系为φM=εM/2sinθcosθ； △D=FDh/8nASEsin3θ 为子模块在竖向荷载作用下的竖向位移，可根据结构上相应的竖向荷载和子模块的竖向刚度计算得出；ε为斜交网筒结构在侧向和竖向荷载作用下子模块角部斜柱产生的应变，设斜柱进入塑性状态时的应变为εa，可根据斜柱材料的属性和截面的参数得出．

由式(15)､(16)可得变形转角的计算式为

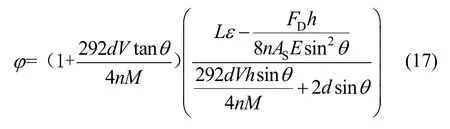
在侧向倒三角形荷载作用下，子模块角部斜柱达到不同的轴向应变时，子模块的变形转角如图8所示(其他荷载分布情况与之相同，故省略)．

图8 侧向倒三角形荷载下各模型变形转角随角部斜柱应变的变化Fig.8 The harmful angle of each model under the lateral inverted triangle load

从图8可以得出，在相同的斜柱应变下，变形转角随着斜柱角度的增大而增大．结构在侧向荷载作用下子模块的变形转角受斜柱角度变化的影响比较明显．当ε=0.3εa时，子模块能够保持在弹性阶段并且具有良好的侧向刚度及变形能力．同理可得其他子模块的变形转角．

3 侧移角限值的讨论

结构的层间位移角是衡量结构的刚度和变形能力的重要指标[9]．我国规范对斜交网格筒结构的层间位移角限值没有明确规定。本节提出通过斜交网格筒结构各子模块的变形转角，来控制结构在弹性阶段时的侧向刚度及变形能力．基于斜交网格筒结构子模块腹板角部斜柱的轴向应变，得出结构在不同的侧向荷载作用下子模块的变形转角，通过斜交网格筒结构各子模块的变形转角，来控制结构在弹性阶段时的侧向刚度及变形能力。

由图8可得，不同斜柱角度的斜交网格筒结构在侧向荷载作用下，子模块角部的斜柱产生相同的轴向应变时，变形转角随着斜柱角度的增大而增大，斜柱角度对变形转角的影响比较明显．对不同斜柱角度的斜交网格筒结构子模块给出一个相同的弹性位移角限值显然是不合理的．本文建议根据结构具体的几何参数，不同斜柱角度的结构子模块应采取不同的弹性位移角限值．

以模型二(75.96°)为例，当底部子模块角部斜柱的应变ε=0.3εa时，由式(17)可得出变形转角分别为φ=1/1136(倒三角形荷载)、φ=1/1214(侧向均布荷载)、φ=1/1220(顶点集中荷载)，在三种不同的侧向分布荷载作用下变形转角均不超过1/1100．所以，可以通过限制该子模块的变形转角小于1/1100，来控制其在弹性阶段时的侧向刚度及变形能力．同理可得该结构其他子模块的变形转角限值．取所有子模块变形转角限值中的最小值，来控制斜交网格筒结构在弹性阶段时的侧向刚度及变形能力．

4 有限元验证

以模型二为例，采用SAP2000结构分析软件对其分别在顶点集中荷载、侧向倒三角形荷载、侧向均布荷载作用下进行静力弹性分析．当结构底部子模块腹板角部斜柱的轴向应变ε=0.3εa时，斜交网格筒结构在三种不同侧向荷载作用下的层间位移角分布如图9所示．

从图9可以得出，结构底部子模块最大层间位移角分别为1/1100(倒三角形荷载)、1/1161(侧向均荷载)、1/1185(顶点集中荷载)，与通过式(17)得到的变形转角φ=1/1136(倒三角形荷载)、φ=1/1214 (侧向均布荷载)、φ=1/1220 (顶点集中荷载)比较吻合，结构底部子模块的层间位移角均小于1/1100，从而验证了本文基于斜交网格筒结构子模块腹板角部斜柱的轴向应变，得出结构在不同的侧向荷载作用下子模块的变形转角的计算方法是比较合理的．随着楼层高度的增大，由于无害层间位移角的积累，所以结构的中上部的层间位移角逐渐增大甚至超出了1/1100．

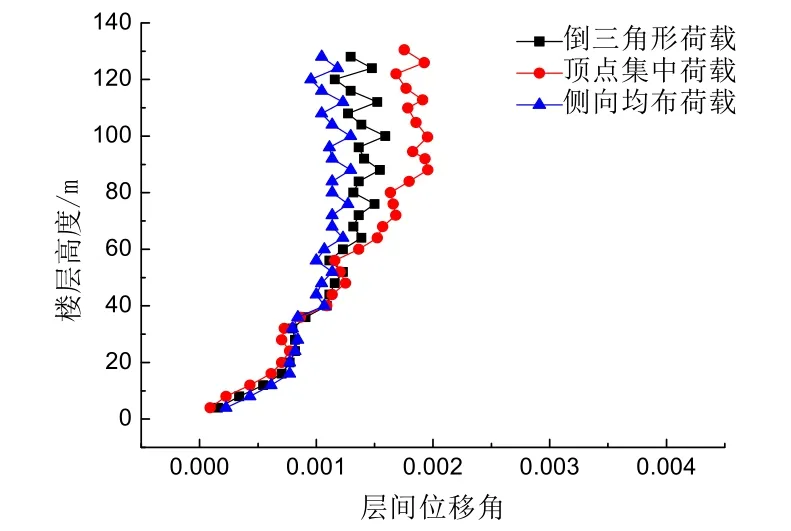
图9 斜交网格筒结构的层间位移角Fig.9 Inter story drift angle of the diagrid tube structure

5 结论

(1) 斜交网格筒结构子模块的剪切刚度和弯曲刚度均随着斜柱角度的增大而减小，剪切刚度受斜柱角度的影响更加明显．斜交网格筒结构的侧向刚度随着斜柱角度的增大而减小．

(2) 推导了斜交网格筒子模块的剪切转角和弯曲转角的计算式以及剪切转角和弯曲转角之间的比例关系，并得出在相同的侧向荷载作用下，随着斜柱角度的增大，剪切转角和弯曲转角逐渐增大，剪切转角与弯曲转角的比值逐渐增大．

(3) 提出了通过斜交网格筒结构各子模块的变形转角，来控制结构在弹性阶段时的侧向刚度及变形能力．通过子模块角部斜柱的轴向应变与子模块变形转角之间的关系，建立了子模块变形转角的计算式．得出在相同的斜柱应变下，变形转角随着斜柱角度的增大而增大．结构在侧向荷载作用下子模块的变形转角受斜柱角度变化的影响比较明显，建议根据结构具体的几何参数，不同斜柱角度的结构应采取不同的弹性位移角限值．

References

[1]周健,汪大绥. 高层斜交网格结构体系的性能研究[J].建筑结构, 2007, 37(5): 87-91.ZHOU JIAN, WANG DASUI. Performance research on high-rise diagonal frame structure〔J〕. Building Structure,2007, 37(5): 87-91.

[2] MOON K S, CONNOR J, FERNANDEZ, et al. Diagrid structural systems for tall buildings: characteristics and methodology for preliminary design[J]. The Structural Design of Tall and Special Buildings, 2007, 16(2):205-230.

[3] 韩小雷, 唐剑秋, 黄艺燕, 等. 钢管混凝土巨型斜交网格筒体结构非线性分析[J]. 地震工程与工程振动,2009, 29(4): 77-84.HAN Xiaolei, TANG Jianqiu, HUANG Yiyan, et al. Nonlinear analysis of huge oblique crossing lattice structure with concrete filled steel tube[J]. Earthquake Engineering and Engineering Vibration, 2009, 29(4): 77-84.

[4] 甄伟, 盛平, 王轶, 等. 北京保利国际广场主塔楼结构设计[J]. 建筑结构, 2013, 43(17): 75-80.ZHEN Wei, SHENG Ping, WANG Yi, et al. Structure design of main tower building of Beijing Poly Plaza[J].Building Structure, 2013, 43(17): 75-80.

[5] 曹正罡, 严佳川, 周威, 等. 中石油大厦斜交网格X型节点试验研究[J]. 土木工程学报, 2012, 45(3): 42-48.CAO Zhenggang, YAN Jiachuan, ZHOU Wei, et a1. Experimental Study on the X-shaped Joints in the Oblique Crossing Lattice of the China Petroleum Building[J].China Civil Engineering Journal, 2012, 45( 3): 42-48.

[6] JINKOOKIM, YOUNG-HO LEE. Seismic performance evaluation of diagrid system buildings[J]. The Structural Design of Tall and Special Buildings, 2012, 21(10).

[7] 赵丰. 高层斜交网筒结构体系基本力学性能研究[D].北京: 清华大学土木工程系, 2012.ZHAO Feng. The basic study of mechanical properties on diagrid tube structural system for high-rise buildings[D].Beijing: Department of civil engineering, Tsinghua University, 2012.

[8] 郭伟亮, 滕军, 容柏生, 等. 高层斜交网格筒-核心筒结构抗震性能分析[J]. 振动与冲击, 2011, 30(4):150-155.GUO Weiliang, TENG Jun, RONG Baisheng, et a1. A seismic behaviour of a diagrid tubecore tube structure[J].Journal of Vibration And Shock, 2011, 30(4): 150-155.

[9] 翁泽松. 高层建筑结构层间位移角限值控制探讨[D].广州: 华南理工大学土木与交通学院, 2014.WENG Zesong. Discussion on the control of the displacement angle between the high rise building structure[D]. Guangzhou: School of civil and transportation engineering, South China University of Technology,2014.