某类铅芯橡胶支座的端部水平动静比研究
吴忠铁,范萍萍, 杜永峰, 王晓琴
(1. 西北民族大学土木工程学院,甘肃 兰州 730050;2. 兰州工业学院土木工程学院,甘肃 兰州 730050;3. 兰州理工大学防震减灾研究所,甘肃 兰州 730050)
橡胶支座作为隔震支座中重要的隔震元件,在隔震结构的动力计算中,铅芯橡胶支座主要选用微分型恢复力模型和双线型模型两类模型,对于这两种模型的研究也相对比较充分[1-6].金建敏等人[7]对铅芯橡胶支座微分型恢复力模型屈服前刚度进行了研究,在理论和试验方面进行了对比分析,建议了相对较为合理的参数.在以往的研究中对于橡胶支座的地震荷载作用下端部剪力(动剪力)和静力荷载作用下端部剪力(静剪力)之间的关系研究的比较少.本文选用橡胶剪切模量为0.6 MPa的一类橡胶支座,以建筑抗震规范[8]的标准为基础,采用铅芯橡胶支座的非线性模型,以铅芯橡胶支座的端部动剪力和静剪力之间的比值(动静比)为衡量指标,研究铅芯橡胶支座的直径、屈服后刚度与屈服前刚度比及其竖向设计荷载等参数对铅芯橡胶支座的动静比的分布范围和变化趋势的影响,初步探讨其动静比与剪切变形之间的关系,给出动剪力简化计算的一般公式,并对剪切变形为 250%时简化计算结果和数值计算结果进行了验算.
1 理论分析
在分析的过程中主要以单个铅芯橡胶支座为研究对象,铅芯橡胶支座的上部质量为m,铅芯橡胶支座模型如图1(a)所示.计算分析模型选用单质点模型.如图1(b)所示,分析过程中非线性模型如1(c)所示.
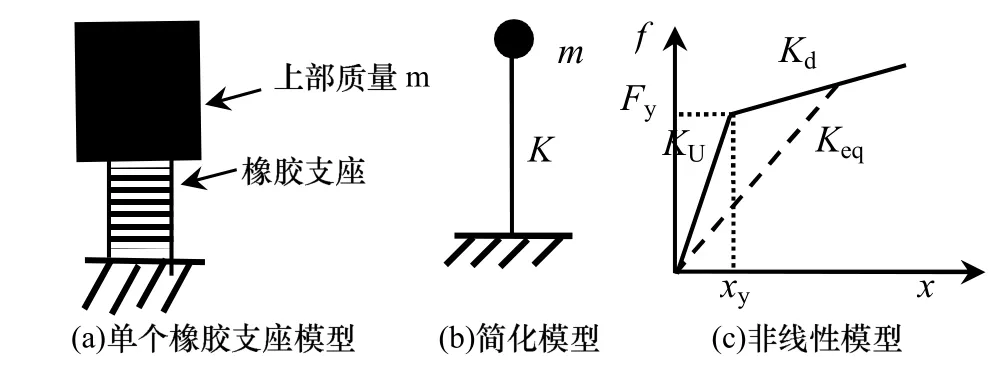
图1 橡胶支座分析模型Fig.1 Analysis model of rubber bearing
铅芯橡胶支座的单质点运动方程:
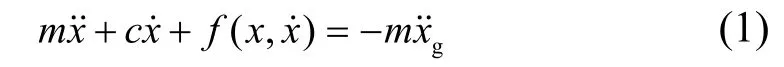
式中:m为铅芯橡胶支座的上部质量.c为铅芯橡胶支座的阻尼系数.f( x, x˙)为铅芯橡胶支座的抗侧力.x、x˙、˙x分别为橡胶支座顶部的相对地面的位移、速度、加速度.˙xg为地震作用时地面加速度.
式(1)中恢复力f( x, x˙),其表达式为
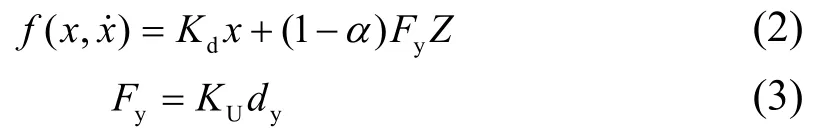
式中:α为LRB屈服后与屈服前的刚度比,KU为LRB的屈服前刚度,Kd为LRB的屈服后刚度,dy为 LRB的屈服位移,Z为考虑材料滞回特性的无量纲分量,其表达式为
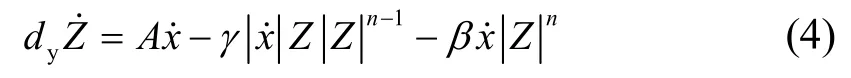
式中:A、γ、β、n为滞回环的无量纲参数.
将方程(2)带入方程(1)可以得到
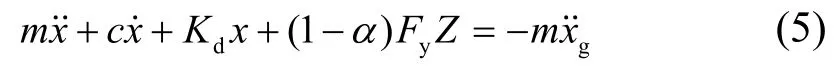
将方程(4)和(5)联立可得求解在地震作用下橡胶支座的动力响应.
为了分析橡胶支座端部动剪力与静剪力的变化关系,将含阻尼项的端部荷载视为橡胶支座的端部动剪力,可表示为
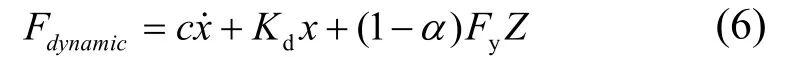
将不含阻尼项的端部荷载视为橡胶支座的端部静剪力,可表示为
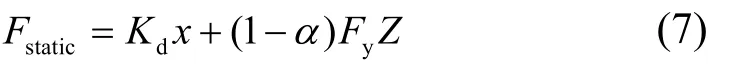
为了表述方便定义在橡胶支座上端部变形相同时橡胶支座的动剪力和静剪力的比值为动静比,用符号λ表示,计算公式可以表示为
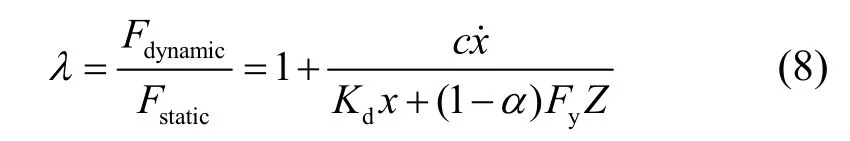
2 参数与地震波
2.1 模型参数的确定与选取
从文献[9]中选取常用的铅芯橡胶支座类型,参数见表 1.在进行地震作用分析时,依据规范[8]的相关规定,其上部质量根据建筑类别确定,甲,乙,丙三类分别对应的竖向设计荷载为10 MPa,12 MPa和15 MPa,其对应的上部质量的计算公式

式中,p为规范[8]中铅芯橡胶支座的竖向设计荷载.DR为铅芯橡胶支座的直径,依据表1中参数选取.g取9.8 N/kg.依据公式(9)计算所得质量,详见表2.
2.2 地震动的确定与选取
本文采用Matlab软件进行动力时程响应分析,并对数据分析结果进行处理.在进行动力时程响应分析时参考美国ATC-40中给出的地震动记录建议,采用了 CHICHI地震中 CHY028 、TCU075 和TCU102三个台站,6条地震波.地震波具体参数如下表3所示.为了研究变形相同时橡胶支座端部动剪力与静剪力的动静比变化关系,充分考虑橡胶支座的非线性行为,依据规范[8]所用地震波幅值均按照罕遇地震下8度加速度峰值510 cm/s2进行调幅.
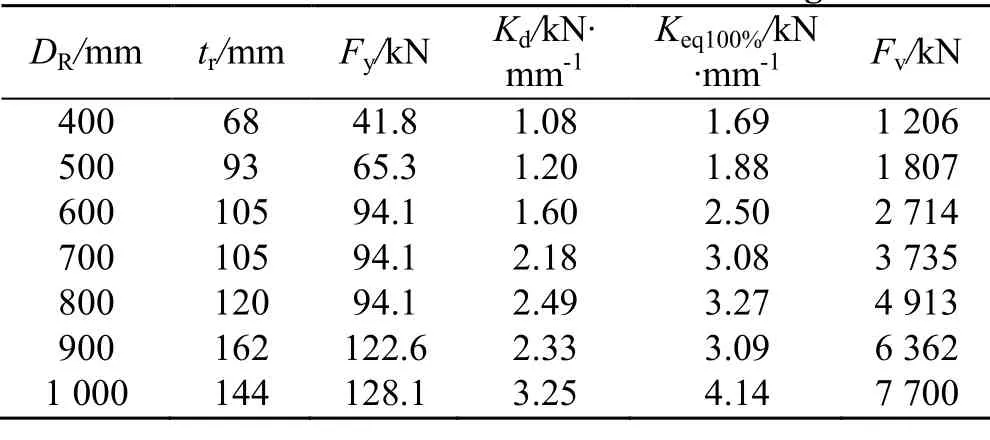
表1 铅芯橡胶支座参数G=0.6 MPaTab.1 Parameters of lead rubber bearing

表2 铅芯橡胶支座上部设计质量/kgTab.2 Mass of the top of lead rubber bearing
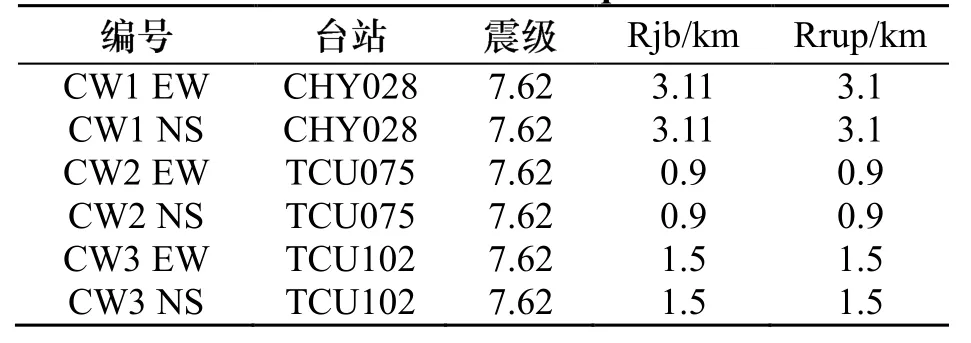
表3 地震波参数Tab.3 Parameters of earthquake waves
3 数值分析与讨论
选用表1中铅芯橡胶支座的参数,以铅芯橡胶支座参数中的直径 DR和屈服后刚度和屈服前刚度比α及竖向设计荷载p为变量,地震波依据选用表3 进行选用,计算公式(4)中系数 A=1、γ=0.5、β=0.5、n=2.上部质量 m选取与建筑类别对应的上部质量.式(1)中的阻尼系数选用质量阻尼c=2mξwn,阻尼比ζ按照普通橡胶支座的阻尼比取0.04.
3.1 不同直径下铅芯橡胶支座的端部水平动静比
图2为不同直径的铅芯橡胶支座在地震作用下水平动静比的分布变化状态.
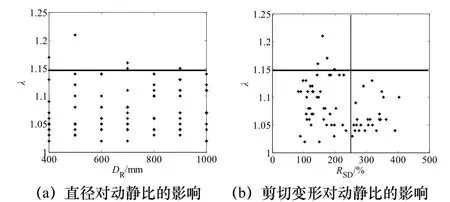
图2 不同直径DR下对铅芯橡胶支座的水平动静比分布(α=0.1,p=12 MPa)Fig.2 Distribution of RHDS under the different diameter DR of lead rubber bearings
从图2(a)中可以看出,铅芯橡胶支座的静动比分布状态受橡胶支座的直径影响不明显.除直径400 mm和500 mm及700 mm的三个点以外,其它动静比数值均在1.15以下,且分布比较均匀.从图2(b)中为不同橡胶支座的剪切变形与其动静比的变化关系.从所有动静比总体变化趋势来看,随着橡胶支座的剪切变形的增大,动静比总体在降低.按照建筑抗震规范规定,当铅芯橡胶支座的剪切变形到250%以后其动静比均在1.15以下.结合图2(a)和图2(b),可知动静比超出1.15时,橡胶支座的剪切变形在150%左右,距大剪切变形250%还有一定的变形空间.且随着剪切变形的增大,同一直径橡胶支座的端部剪力是持续增大,直至支座破坏.
4.2 不同屈服后刚度与屈服前刚度比下铅芯橡胶支座的端部水平动静比
图3为不同的屈服后刚度与屈服前刚度比α对铅芯橡胶支座的端部水平动静比的影响,主要从 α和剪切变形两个方面来反映动静比的变化趋势和分布状态.
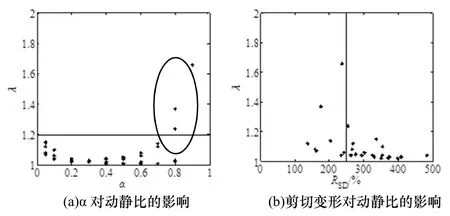
图3 不同屈服后刚度与屈服前刚度比α下铅芯橡胶支座的水平动静比分布(DR=600 mm,p=12 MPa)Fig.3 Distribution of RHDS under the different ratio α between non yield stiffness and post yield stiffness of lead rubber bearings
从图3(a)中可以看出,铅芯橡胶支座的动静比呈一个抛物线的趋势,在 α=0.3时动静比基本在1.02附近.在α=0.9时动静比在1.7附近.在α从0.05到0.9整个分布区间上,除了圆圈中的三个点,铅芯橡胶支座的动静比基本分布在1.2以下.根据铅芯橡胶支座的屈服后刚度与屈服前刚度比的特点,较理想的数值基本在α=0.1附近[7],此时动静比基本在1.15附近.从图3(b)中可以看出,在不同的铅芯橡胶支座的屈服后刚度与屈服前刚度比α下随着剪切变形的增大铅芯橡胶支座的动静比降低.当铅芯橡胶支座的剪切变形达到 250%以后,其动静比在1.25以下.
4.4 不同竖向设计荷载下铅芯橡胶支座端部动静比
图4为不同的竖向荷载p下铅芯橡胶支座的水平动静比的变化趋势和分布状态.
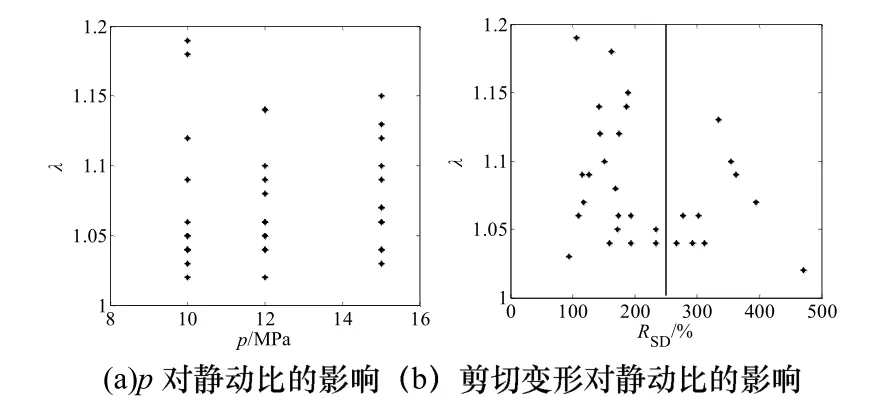
图4 不同竖向荷载p下铅芯橡胶支座的水平动静比分布(DR=600 mm,α=0.1)Fig.4 Distribution of RHDS under the vertical load p of lead rubber bearings
图4(a)分别是竖向设计荷载为 p=10 MPa,12 MPa,15 MPa下铅芯橡胶支座的动静比的变化与分布形式,从动静比的数值上来看,当p=10 MPa时,铅芯橡胶支座的动静比最大值为1.19,当p=12 MPa时,铅芯橡胶支座的动静比最大值为1.14,当p=12 MPa时,铅芯橡胶支座的动静比最大值为1.15.图4(b)为不同的竖向荷载下铅芯橡胶支座的动静比随剪切变形的变化趋势和分布状态.总体来看,随着剪切变形的增大铅芯橡胶支座的动静比降低.当剪切变形到 250%以后,铅芯橡胶支座的静动比在1.135以下.
4.5 铅芯橡胶支座端部的动剪力简化计算一般公式
为了简化铅芯橡胶支座端部水平动剪力的计算过程,依据公式(8)给出铅芯橡胶支座的动剪力简化计算公式:

式中:Fds为简化计算的铅芯橡胶支座的水平动剪力,Fs为橡胶支座的水平静剪力,λ为不同状态时铅芯橡胶支座的动静比.为了分析公式(10)的合理性,给出铅芯橡胶支座剪切变形为 250%时简化计算公式(10)与实际分析端部水平动剪力数值之间的关系,依据上述分析结果建议动静比λ250%取值为1.25.计算结果如图5所示.
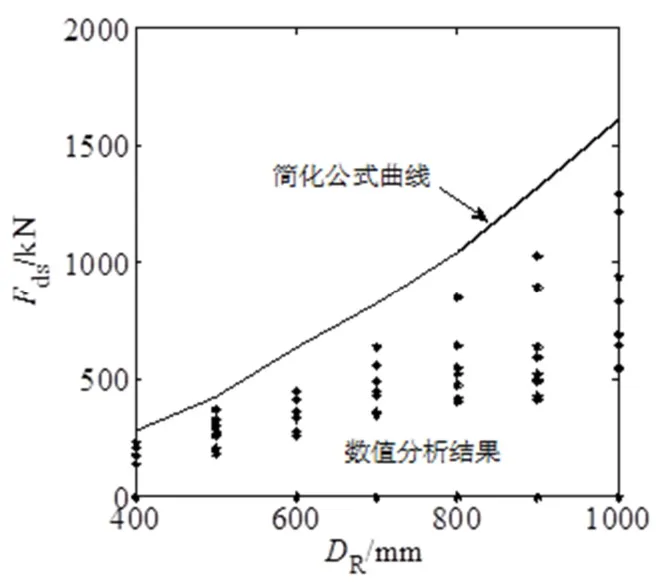
图5 简化公式与数值分析结果对比(λ250%=1.25)Fig.5 Comparison of simplified formula curve and numerical analysis result
从图5中可以看出,简化公式计算结果曲线能将剪切变形 250%时所有的数值分析结果很好的包含在内,且曲线的变化趋势与数据点的变化趋势基本一致.从曲线的变化情况来看,简化公式的计算结果具有一定的安全储备.简化公式(10)可以作为估算某种状态下铅芯橡胶支座的端部动剪力的参考依据.
5 结论
通过上述理论与数值分析可以得到以下结论:
(1) 铅芯橡胶支座的参数对其端部水平动静比均有影响,其中,屈服后刚度与屈服前刚度比对其动静比影响比较明显;
(2) 在不同的参数下铅芯橡胶支座的端部水平动静比随着剪切变形的增大而降低,当铅芯橡胶支座的剪切变形为250%时动静比均在1.25以下;
(3) 通过剪切变形在250%时的数据分析,验证了简化计算一般公式的可靠性,简化计算公式可以作为通过静力状态下端部剪力估算地震作用下端部剪力的参考依据.
References
[1] 党育, 杜永峰, 李慧. 隔震支座连接处的设计[C]//天津:天津大学, 第十三届全国结构工程学术会议, 2004:23-27.DANG Yu, DU Yong feng, LI Hui. A practical design method of isolated bearing joint[C]//Tianjin: Tianjin University, Proceeding of 13th national conference on structure engineering, 2004: 23-27.
[2] BOUC R. Forced vibration of mechanical system with hysteresis, Abstrcat [C]//Proceeding of 4th conference on nonlinear oscillation, Prague, Czechoslovakia, 1967.
[3] WEN Yikwei. Method for random vibration of hysteretic system [J]. Journal of the Engineering Mechanics Division, ASCE, 1976, 102, 249-263.
[4] PARK Y J, WEN Y K, ANG A H-S. Random vibration of hysteretic systems under bi-directional ground motions[J]. Earthquake Engineering and Structural Dynamics,1986, 14: 543-557.
[5] 唐家祥, 刘再华. 建筑结构基础隔震[M]. 武汉: 华中理工大学出版社, 1993.TANG Jiaxiang, LIU Zaihua. Base isolation building structure[M].Wuhan: Huazhong University of Science and Technology Press,1993.
[6] 王斌, 蒋东红, 刘之洋. 减震结构中橡胶垫水平刚度的变化对动力分析的影响[J]. 工业建筑, 1999, 29(6):13-16.WANG Bin, JANG Donghong, LIU Zhiyang. Influence from change of the rubber bearing level stiffness in dynamic analysis of isolation structure[J].industrial construction, 1999, 29(6): 13-16.
[7] 金建敏, 周福霖, 谭平. 铅芯橡胶支座微分型恢复力模型屈服前刚度的研究[J]. 工程力学, 2010, 27(9): 7-13.JIN Jianmin, ZHOU Fulin, TAN Ping. Study on preyield shear stiffness of differential restoring force model of lead rubber bearing [J].Engineering Mechanics, 2010,27(9): 7-13.
[8] GB50011-2010建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.GB50011-2010 Code for seismic design of buildings [S].Beijing:Building Industry Press of China, 2010.
[9] 党育, 杜永峰, 李慧. 基础隔震结构设计及施工指南[M]. 北京: 中国水利水电出版社, 2007: 242-255.DANG Yu, DU Yongfeng, LI Hui. Base isolation structure design and construction guide [M].Beijing: China Water &Power Press, 2007:242-255.

