平面阵列米波雷达超分辨测高技术研究∗

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

由于米波雷达波长较长,因此具有良好的反隐身和抗反辐射导弹的优势频段[1],对雨、雾和云的穿透能力也较强,对于在视线以下或遮蔽物(树木等)后方处于电波阴影区的目标[2],仍有一定的探测能力,因此越来越受到世界各国的重视。但由于其波束较宽,通常会波束“打地”,产生多径干涉效应,发生波瓣分裂,因此会降低雷达的测高精度。

随着阵列超分辨技术的发展,对于规则的平面阵列,与阵列几何模型匹配的最大似然阵列超分辨算法可以有效地解决米波雷达低仰角测高的难题[3],但对于不规则的平面阵列,由于每一行的天线阵元数不同,天线阵面变为不规则的形状,使其在进行测高处理时,如果直接应用这种方法,会得到很差的测高效果。本文通过对最大似然超分辨算法进行改进,使其对不规则阵面的测高精度有了大幅度的提高。

本文首先给出了雷达的阵列回波信号模型,然后提出了基于不规则阵面的与阵列几何模型匹配的最大似然超分辨改进方法,最后给出了理论仿真结果,验证改进方法的有效性。

1 信号模型

针对N个天线阵元组成的垂直均匀线阵(ULA),阵元间距为d,有K个远场窄带信号源,波长为λ,阵列接收到的回波信号包括直达波信号和地面反射波信号,第k(k=1,2,…,K)个信号源入射阵列的直达和反射俯仰角分别为θdk和θsk,平面几何模型[4]如图1所示。

图1 平面反射几何模型示意图

阵列在第l个采样时刻接收的N×1维回波信号矢量[5]为

式中,sdk(t l)和ssk(t l)分别为第k个信号源直达波和反射波的复包络;ρk为第k个信号源对应反射面的反射系数;e(t l)为与回波信号不相关的复高斯白噪声矢量;a(θdk)为阵列对第k个信号源的N×1维直达波导向矢量,且

a(θsk)为阵列对第k个信号源的N×1维反射波导向矢量,且

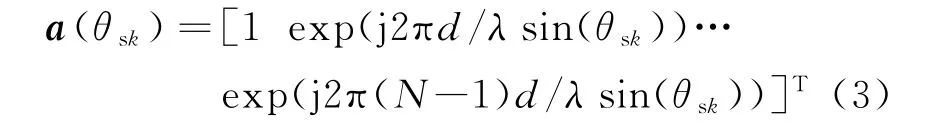
则L个快拍的阵列接收数据矩阵为

2 平面阵列米波雷达测高方法

根据最大似然超分辨测高算法准则[6],对信号源直达入射角θdk的最大似然估计为

式中,P A(θ)是投影到A(θ)的列矢量所展成的信号子空间的投影算子;^R是阵列接收信号自相关矩阵的极大似然估计,它们分别为

式中,A(θ)为N×K维阵列导向矢量矩阵,L为阵列的快拍数。

文献[3]指出,多径信号入射角θsk可以通过直达波入射角θdk、目标的斜距Rd及天线架高hr进行解算,即

然后根据信号模型重新构建阵列导向矢量,进行最大似然超分辨测高。

但对于不规则的平面阵列,如果直接应用上述方法构建阵列导向矢量,进行最大似然超分辨测高,会得到比较大的测高误差,完全不能应用于工程实现当中。

在进行超分辨测高前,需要对天线阵面的每一行天线接收到的回波信号进行行合成,由于每一个天线阵元接收的回波信号幅度是相近的,且每一行天线的阵元数是不同的,因此对每一行天线接收到的回波信号进行行合成后,其对应的行合成信号幅度会有很大的差别。对于方位维左右不对称的阵面,每一行天线接收到的回波信号在进行行合成时,需要以任一垂直线与每一行的交点为对应行的参考点进行行合成,使各行回波信号进行行合成后在一条垂直线上。

对于不规则平面阵列行合成后信号幅度差别比较大,进而导致测高精度比较差的问题,可以通过在行合成时对每一行合成的信号幅度进行归一化来解决,而对阵列信号的导向矢量进行行幅度归一化也可以达到相同的效果。

假设对于上面的信号模型,从下往上每一行天线的阵元数分别为(M1,M2,…,M N),且M=max(M1,M2,…,M N),则每一行天线的幅度归一化导向矢量系数为

则直达波和反射波导向矢量分别为

以上这种改进方法,不仅对不规则的平面阵列适用,而且对于规则平面阵列依然适用,因此其可以应用于所有的平面阵列进行高度估计。

基于平面阵列的米波雷达测高改进方法可以归纳为如下几个步骤:

第一步 对各行回波信号进行行合成,使其合成后在一条垂直线上。

第二步 根据各行天线阵元数,按照式(8)～(11)计算各行天线的幅度归一化导向矢量系数,并重新构建阵列导向矢量。

第三步 按照式(5)进行最大似然超分辨测高。

3 计算机仿真

为了验证基于平面阵列的米波雷达测高改进方法的有效性,给出了计算机仿真结果。仿真所使用的阵列为22行且各行天线阵元数不同的平面阵列,行间距d=0.7λ,λ=1.0 m,平坦地面的反射系数ρ=-0.95,回波快拍数为10,采样率为1 MHz,地形起伏为-1.5～1.5 m。

实验1 相同距离、不同仰角条件下,算法的统计性能分析

目标距离固定为300 km,高度在7～16 km(仰角在0.32°～2.1°)之间变化,进行200次 Monte-Carlo实验。图2给出了目标测角和测高均方根误差随着目标高度的变化曲线。从图中可以看出,目标高度在1.14 km(仰角1.16°)以上,改进前后的测高均方根误差相近,且均在600 m以内;目标高度在8.6～11.4 km(仰角在0.63°～1.16°)之间,改进后的测高均方根误差减小了200 m左右;目标高度在8.6 km(仰角0.63°)以下,改进后的测高均方根误差有了大幅度的降低。

实验2 相同高度、不同距离条件下,算法的统计性能分析

目标高度固定为8 km,距离在100～300 km(仰角在4.3°～0.5°)之间变化,进行 200次Monte-Carlo实验。图3给出了目标测角和测高均方根误差随着目标距离的变化曲线。从图中可以看出,目标距离在220 km以内(仰角1.34°以上),改进前后的测高均方根误差相近,且均在400 m以内;目标距离在220 km以外,改进后的测高均方根误差有了大幅度的降低。

4 结束语

针对不规则的平面阵列米波雷达直接应用最大似然超分辨算法测高误差比较大的问题,本文提出了一种增加各天线的幅度归一化导向矢量系数的方法,来降低雷达的测高误差,进而推广到所有的平面阵列,并给出了计算机仿真结果,验证了改进方法的有效性,可以有效地解决不规则平面阵列米波雷达低仰角测高的难题。

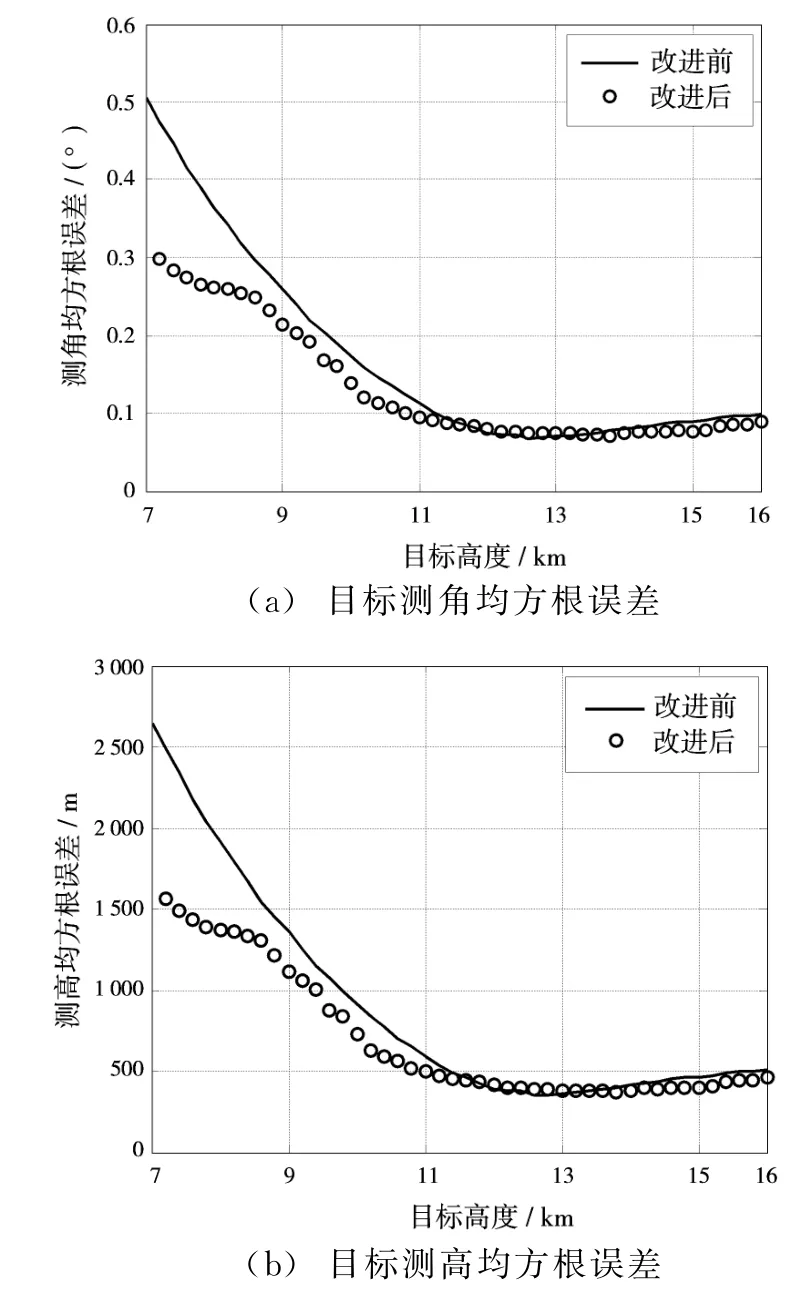
图2 固定距离仿真数据处理结果

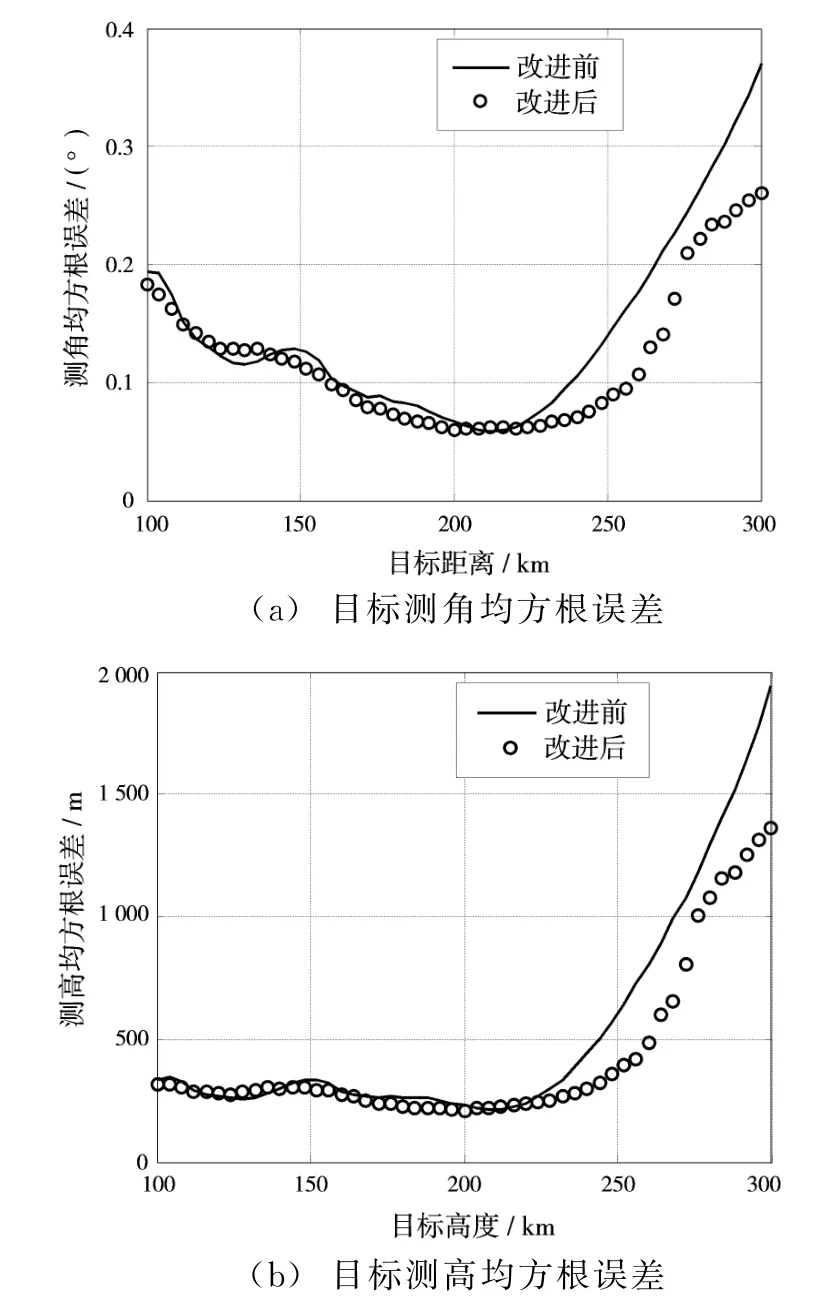
图3 固定高度仿真数据处理结果

[1]KUSCHEL H.VHF/UHF Radar Part1:Characteristics[J].Electronics&Communication Engineering Journal,2002(4):61-72.

[2]谭怀英,郭建明.VHF/UHF雷达特性及其应用[C]∥中国雷达技术论坛,南京:[出版者不详],2006:83-87.

[3]刘张林,陈伯孝,杨雪亚,等.米波雷达最大似然超分辨测高技术研究[J].雷达科学与技术,2011,9(4):308-310.

[4]BARTON D K.雷达系统分析与建模[M].南京电子技术研究所,译.北京:电子工业出版社,2007:204-206.

[5]杨雪亚,杨广玉.基于稀疏解的米波雷达测高方法[J].雷达科学与技术,2012,10(6):629-632.

[6]刘德树,罗景青,张剑云.空间谱估计及其应用[M].合肥:中国科学技术大学出版社,1997:21-23.