基于斑马图的天基雷达PRF设计

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

天基雷达突破了机载战场监视雷达的空间限制,可以不受作战实际控制空域和国界的约束,具备大范围、全天候的监视能力,极大改善对远程低空、超低空甚至地/海运动目标的探测性能,目前受到军用和民用的广泛关注[1-2]。

脉冲重复频率(PRF)是天基雷达总体设计中一个重要的参数,而PRF设计受到很多因素的制约,例如距离模糊度、多普勒模糊度、星下点的回波和发射脉冲的遮挡等。一般天基雷达PRF设计是诸多约束相互制约的一个折中选择[3]。文献[4]指出,天基雷达采用中PRF能够获得较好的探测性能,并给出了相应算法解距离模糊和速度模糊。但是只是定性分析了设计中所考虑的因素,没有进行理论推导和仿真验证。文献[5]主要从空时自适应(STAP)杂波抑制的角度提出了天基雷达PRF设计准则。

天基雷达PRF设计中星下回波和脉冲遮挡应为首要考虑的限制因素。本文主要借助机载雷达和SAR系统中利用斑马图进行PRF设计的方法[6-7],合理地选择PRF,使得星下点回波约束在发射脉冲与有用回波信号录取窗口之间,并且观测区域有用回波信号录取窗口位于发射脉冲重复周期之间,为天基雷达PRF设计提供参考。

1 天基雷达星-地模型

在天基雷达轨道计算和覆盖区域计算中,地球要作为椭球体处理,这里为了说明其原理,假设地球为均匀球体,其半径为R,其几何关系如图1所示,O为地心,A为卫星,B为星下点,C为观测近地点,D为观测远地点。H表示天基雷达的高度,Rn,Rf分别表示观测区域的最近和最远斜距,对应的回波时间分别为Tn,Tf;αn,αf分别表示最近最远对应的最小和最大视角;相应的最小和最大入射角分别为θn,θf;对应的地心角分别为βn,βf;τ为脉宽,τg为保护时间带,c为光速。

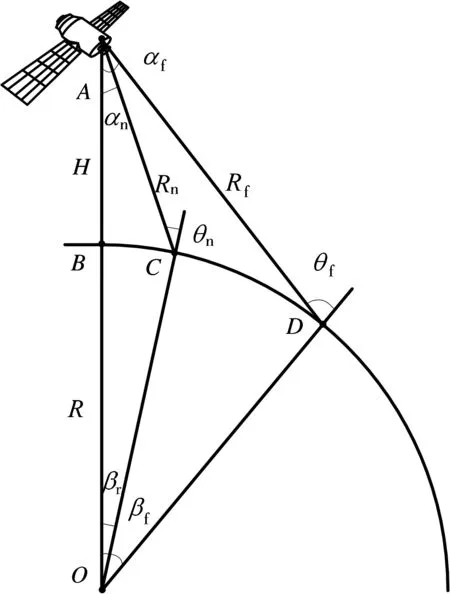
图1 天基雷达星地模型示意图

由图1中的几何关系,我们容易得到以下几个结论:

则最近和最远距离对应的回波时间可以表示为

星下点回波时间可以表示为

2 天基雷达回波模型及PRF约束

对于发射和接收共用一套天线的天基雷达系统,由于在任何时刻空中同时有发射脉冲、星下点脉冲和回波,必须对PRF加以限制,使发射脉冲、星下点脉冲不落在回波窗之中。图2给出了天基雷达时序图。

图2 天基雷达回波时序图

为此,发射脉冲对PRF的约束可表示为

式(8)、(9)、(10)中fr表示脉冲重复频率,函数Frac(·)和Int(·)分别表示取小数和整数部分。

星下点回波的约束为

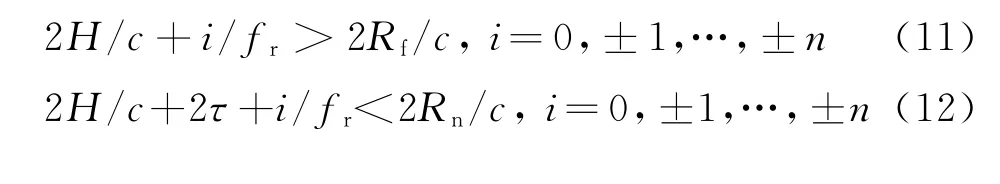
式(11)和式(12)中n为发射脉冲数。

为了给出入射角与PRF关系的曲线,需要给出一定的PRF范围,frn和frr分别表示所选择的最小和最大的可能脉冲重复频率。下面计算发射信号的前后沿时间,分别用T1和T2表示:

式中:Tr表示脉冲重复周期;i=imin,imin+1,…,imax,imin=Int(Tn·frn),imax=Int(Tf·frf)。

计算星下点信号前后沿回波时间,分别用Tnad1和Tnad2表示:

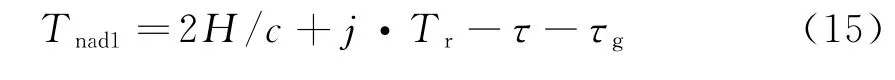
式中,j=jmin,jmin+1,…,jmax,jmin=imin-Int[(Tnad+τ+2tg)·frn],jmax=imax-Int(Tnad·frf)。

综合式(5)至式(16)可得在PRF与入射角θ所确定的二维平面上给出星下点回波和被发射脉冲遮挡区的位置,而这些位置不能落在观测区域内。星下点回波与发射脉冲遮挡区在PRF-θ二维平面上表现为相互交错的条带,因交错的条带与斑马条纹相似,故称为“斑马图”。

3 修正的斑马图

上节分析了斑马图的基本原理,但是在实际应用中,上述几点假设需要进行修正。由于地球是椭球体,并且卫星运行的轨道也一般为椭圆,轨道上每个星下点的高度也是不同的。由于斑马图取决于卫星高度,因此在不同纬度上,斑马图是不同的,PRF的选择相应地需要进行变化。下面对卫星轨道进行分析,给出卫星高度的变化规律,得到修正的斑马图。

卫星运动的轨道方程可以表示为

可见卫星轨道是一个以地心为其一焦点的椭圆。f为真近点角,大小为自极轴正方向(近地点方向)转至动径r方向所转动的角度。因此。轨道要素如图3所示:O为地心,S为卫星所处位置,N为近地点,A为升交点,升交点方向和近地点方向的夹角ω为近地点幅角,它确定了轨道椭圆在轨道平面内的位置。而卫星轨道中的具体位置由真近点角f来确定,通常也用轨道时间参数t来描述。

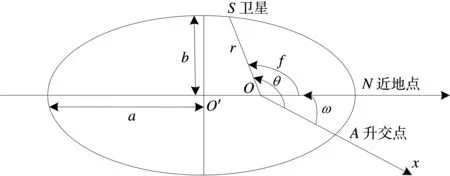
图3 卫星椭圆轨道参数

根据开普勒积分,可得

式中:E为偏近地角为卫星运动的平均角速度,a为椭圆轨道长半轴,G为万有引力常数,M为地球质量;t a为卫星运动时间的起点。

用牛顿迭代法可确定任意时刻t所对应的E(t)。真近点角f(t)和偏近点角E(t)的关系为

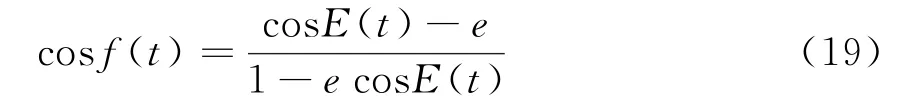
再利用式(17)可以得到轨道半径r(t),则任意时刻轨道高度可表示为

式中,R(t)为对应时刻卫星星下点的地球半径。这样可以得到任意时刻星下点的高度,由此确定相应的斑马图。

4 仿真分析

设天基雷达其轨道平均高度H=500 km,轨道离心率e=0.003,计算出轨道长半轴长a=6 878 km,近地点高度hn=479.37 km,远地点高度hf=520.63 km。另外设所选择的最小和最大可能的脉冲重复频率frf=4 500 Hz,frn=1500 Hz,感兴趣观测带对应的最小、最大入射角分别为θn=15°,θf=55°;脉冲宽度τ=33μs,保护时间带分别为τg=0.1τ和τg=0.5τ。根据这些参数,得到仿真斑马图如图4所示,其中图4(a)对应为保护时间带τg=0.1τ,图4(b)对应为保护时间带τg=0.5τ。图4中,粗线对应为星下点回波,细线对应为发射脉冲遮挡。对比两图可知:在卫星高度和发射脉冲宽度不变的情况下,脉冲保护带越宽,星下点回波宽度越宽和发射脉冲遮挡越严重,重频可选区域越小;但同时也可以看出,条纹的相对位置没有发生变化。图中菱形区域为可选区域,如图所示给出一些可以选择的重频区域,用黑线进行了标记;当然,重频最终选择还应根据距离、方位模糊度等指标加以选择。

图4 不同保护时间带τg条件下斑马图

图5给出了当卫星分别处于近、远地点时的斑马图,其中图5(a)为近地点斑马图,图5(b)为远地点斑马图。对比图4(a)、图5(a)和图5(b)比较可知,随着高度h(t)的增加,星下点回波在斑马图中向左平移,而发射脉冲遮挡条纹向右上方平移,这样PRF选择空间也不相同。因此在卫星运行的一个周期内,斑马图会随着卫星高度变化而发生缓慢的变化,重频选择相应需要进行改变。根据本文所列出的公式,可自适应地形成斑马图,从而为不同波位的重频选择提供参考。

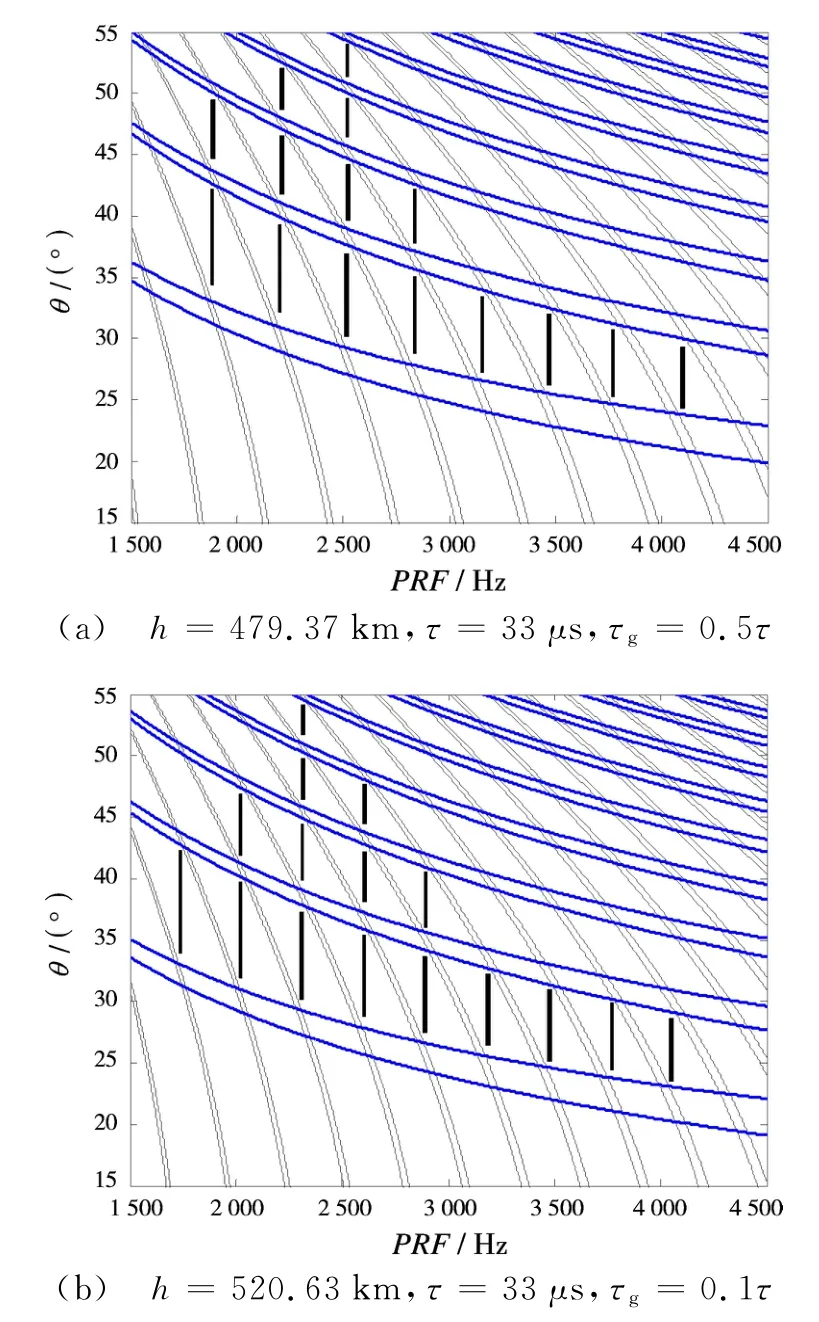
图5 不同时刻条件下斑马图

5 结束语

在天基雷达的总体设计中,脉冲重复频率的选择对于雷达工作非常重要。本文将机载雷达和SAR系统中的基于斑马图的脉冲重复频率设计引入天基雷达系统,并且对传统的斑马图进行了修正以适用于天基雷达系统。对脉宽保护时间和星下点高度等因素对斑马图的影响进行了仿真分析。仿真结果表明,修正的算法能够为天基雷达提供自适应斑马图,为天基雷达PRF选择提供参考。

[1]LANE S A,MURPHEY T W,ZATMAN M.Overview of the Innovative Space-Based Radar Antenna Technology Program[J].Journal of Spacecraft and Rockets,2011,48(1):135-145.

[2]朱庆明,金术玲,孟祥玲.国外天基预警雷达系统发展现状及关键技术[J].电讯技术,2012,52(6):1054-1058.

[3]汤春林.天基AMTI雷达信号处理若干关键技术研究[D].成都:电子科技大学,2012.

[4]罗倩,闫鸿慧.天基雷达的PRF设计[J].舰船电子对抗,2009,32(1):89-91.

[5]张乔,汤俊,彭应宁.基于STAP杂波抑制的天基雷达PRF设计[J].雷达科学与技术,2011,9(5):441-446.

[6]刘永坦.雷达成像技术[M].哈尔滨:哈尔滨工业大学出版社,1999.

[7]ALABASTER C M,HUGHES E J,MATTHEW J H.Medium PRF Radar PRF Selection Using Evolutionary Algorithms[J].IEEE Trans on Aerospace and Electronic Systems,2003,39(3):990-1001.