基于随机阵列的相控阵T/R组件排布方法∗

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室,湖南长沙410073)

0 引言

对于有源相控阵雷达而言,考虑到系统的造价成本,往往利用较少的T/R单元填充阵面,而剩余的位置由R组件填充,在这种条件下有必要研究T/R单元的稀布问题,使得发射方向图在抑制栅瓣、降低副瓣方面获得“最优”性能。

对于阵元稀布问题,Skolnik等人[1]提出了密度加权阵方案,以一个幅度加权阵列为基础控制阵元排布。另一种解决办法是随机阵列,其阵元位置满足某一概率分布。文献[2]分别从一维随机阵列的方向图形成、平均方向图和方向图的平均功率研究随机阵列方向图形成的特点。文献[3-4]以随机阵列为基础,使用遗传算法分别对阵元的位置和权值进行了优化,达到抑制旁瓣的效果,但并没有对随机阵列本身进行研究。文献[5]中研究了随机平面阵的副瓣水平并通过仿真和实际实验验证了结果。文献[6]中提到副瓣水平会影响雷达的作用距离和探测精度,所以需要在副瓣水平方面对稀布阵进行优化。

本文基于随机阵列理论,首先基于文献[2]中的一维随机阵列推导了二维随机阵列方向图形成,说明通过阵元位置的随机分布可以控制方向图。再考虑阵元间的最小间隔,提出了一种最短距离排布方法,这种排布方法可以保证随机阵列方向图的性能,相比于密度加权阵也有一定的性能提升。

1 二维随机阵列波束形成

考虑一般性二维阵列,如图1所示,圆圈代表阵元,共N个。第n个阵元的坐标为(xn,yn),向俯仰角为φ、方位角为θ的方向发射电磁波,假设各阵元方向图无方向性,则阵列方向图可以写成:

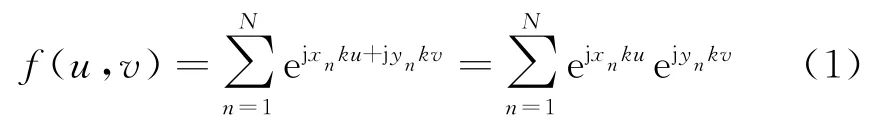
式中,u=sinθcosϕ,v=sinθsinϕ,k=2π/λ。

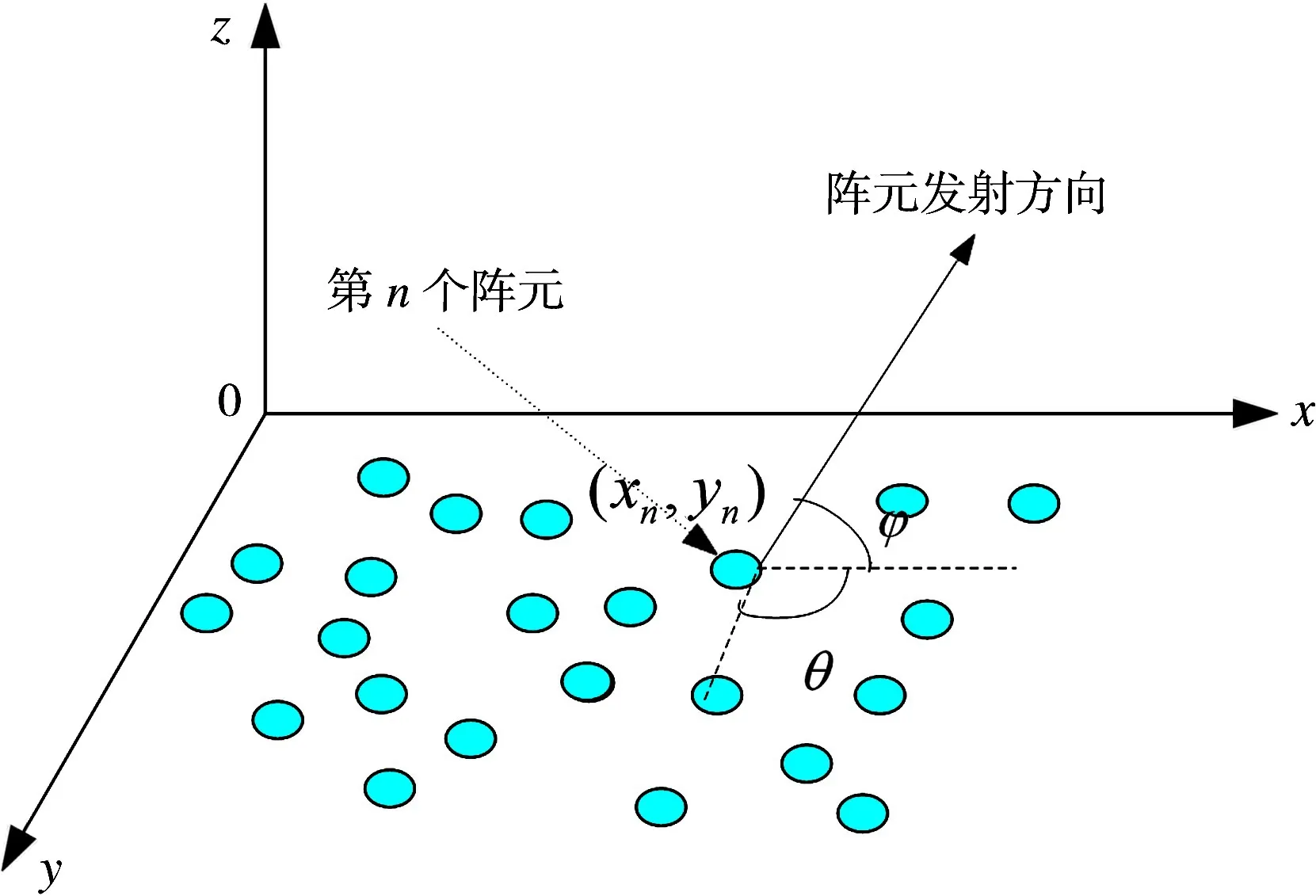
图1 二维阵列

若阵元的坐标为随机变量(Xn,Yn),则此阵列为二维随机阵列,方向图可以写成:

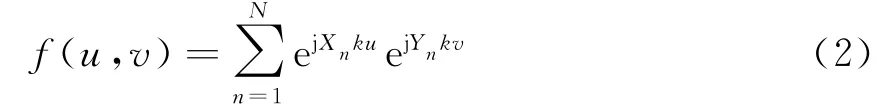
由式(2)可知,二维随机阵列的方向图是N个矢量的叠加,当阵元数一定时,主瓣的峰值高度确定。由于阵元位置的随机性,各角度副瓣的平均高度相同,并以此高度随机变化,所以实际方向图是在平均方向图的基础上变化。写出阵列的平均方向图:

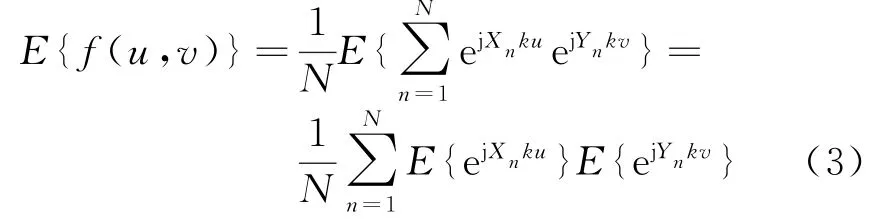
二维随机阵列的平均方向图是由多个随机量ejXnku和ejYnkv取平均叠加得到的。设各个阵元位置的横坐标和纵坐标都是独立同分布,那么就有

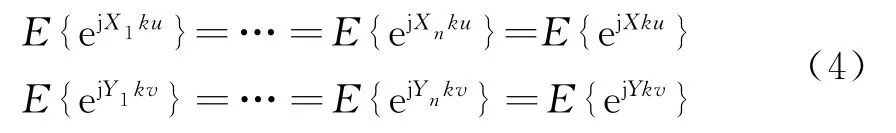
所以,平均方向图可以写成:

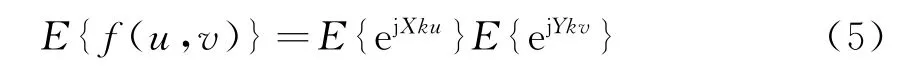
根据概率公式可以得到

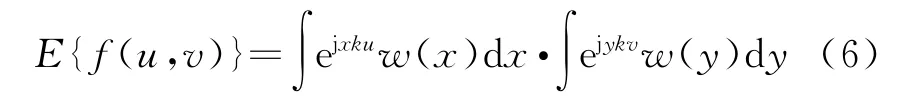
式(6)说明:二维随机阵列的平均方向图只与阵元所服从的随机分布有关。而方向图在其基础上随机变化,如果随机分布给定,随机阵列的平均方向图就确定,则阵元的位置分布会影响实际方向图,所以可找到相对较好的概率分布优化方向图。然而,在随机阵排布时,需要将阵元排布在满足最小间隔的栅格内,会出现两个问题:一是阵元的随机位置在阵面范围之外,二是阵元生成的位置距离很近使得同一个栅格需要排布多个阵元。需要一种排布方法,解决两个问题的同时保证阵元的随机性。

2 二维阵列阵元排布方法

2.1 密度加权阵阵元排布方法

常见的阵元稀布方法是密度加权阵[7-10],其核心思想是:用一个稀布阵来实现一个幅度加权阵的效果。密度加权阵最为常见的一种方法是独立采样法[11]:假设阵元的位置函数为P(x,y),幅度加权阵的幅度分布为A(x,y),则P(x,y)可以表示为

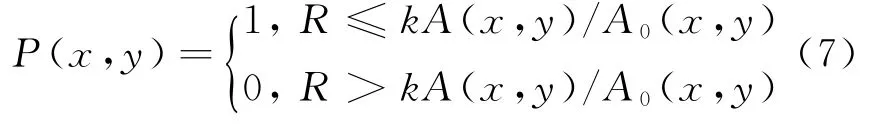
式中,R为在[0,1]间服从均匀分布的随机数, A0(x,y)是A(x,y)中的最大值,k为常系数,与预期的阵元数有关。P(x,y)=1表示在(x,y)处排布阵元。由式(7)可知,密度加权阵实现需要幅度加权阵为基础,排布的阵元数依赖于k。

2.2 随机阵列阵元排布方法

针对随机阵列中阵元排布存在的两个问题,有以下解决办法。

对于阵元落在阵面外的问题,最直接的办法就是调节随机分布的参数使得落在阵面外的阵元尽量少,然后舍去落在阵面外的阵元。但舍去阵元必定会影响方向图,不具有适应性。

对于第二个问题,一种可行的解决办法是用一个阵元通过多倍激励达到多个阵元排布在同一个栅格内的效果。但此方法需要幅度加权,而实际中幅度加权是通过功率衰减来实现,这样减少了雷达作用距离,并且阵面T/R组件的性能也不一致,更换维修也更加困难。

本文基于随机阵列理论,针对两个问题提出一种最短距离排布的方法:当生成一个随机位置时,将阵元排布至与此位置距离最近的栅格内,如果此栅格已经排布了阵元,则搜索阵面中所有未排布阵元的栅格,找出其中与随机位置距离最近的栅格,将阵元排布至栅格内。此处栅格与随机位置的距离指的是栅格中心点与随机位置点之间的距离。最短距离排布在排布阵元时保证了阵元的随机性,同时全部阵元在阵面内。

阵元的排布方法可以分为以下几步:

第一步,设定需要排布的阵元数N。

第二步,将阵面栅格化,得到所有栅格的中心点坐标(x,y)。

第三步,标记每个栅格内有无阵元,根据概率分布随机生成单个阵元位置(x0,y0)。

第四步,根据最短距离式排布的方法搜索距离其最近且未排布阵元的栅格位置(x,y),将阵元排至此栅格内。

第五步,判断阵面内排布的阵元数是否达到N。如果达到,则完成排布;如果不足,则从第三步继续进行排布。

排布方法流程图如图2所示,排布方法示意图如图3所示。

最短距离排布可以用于任何随机分布的阵元排布,即使阵元位置不是随机分布,此方法也有一定的适用性。并且相比于密度加权阵,最短距离排布可以精确控制阵元数。

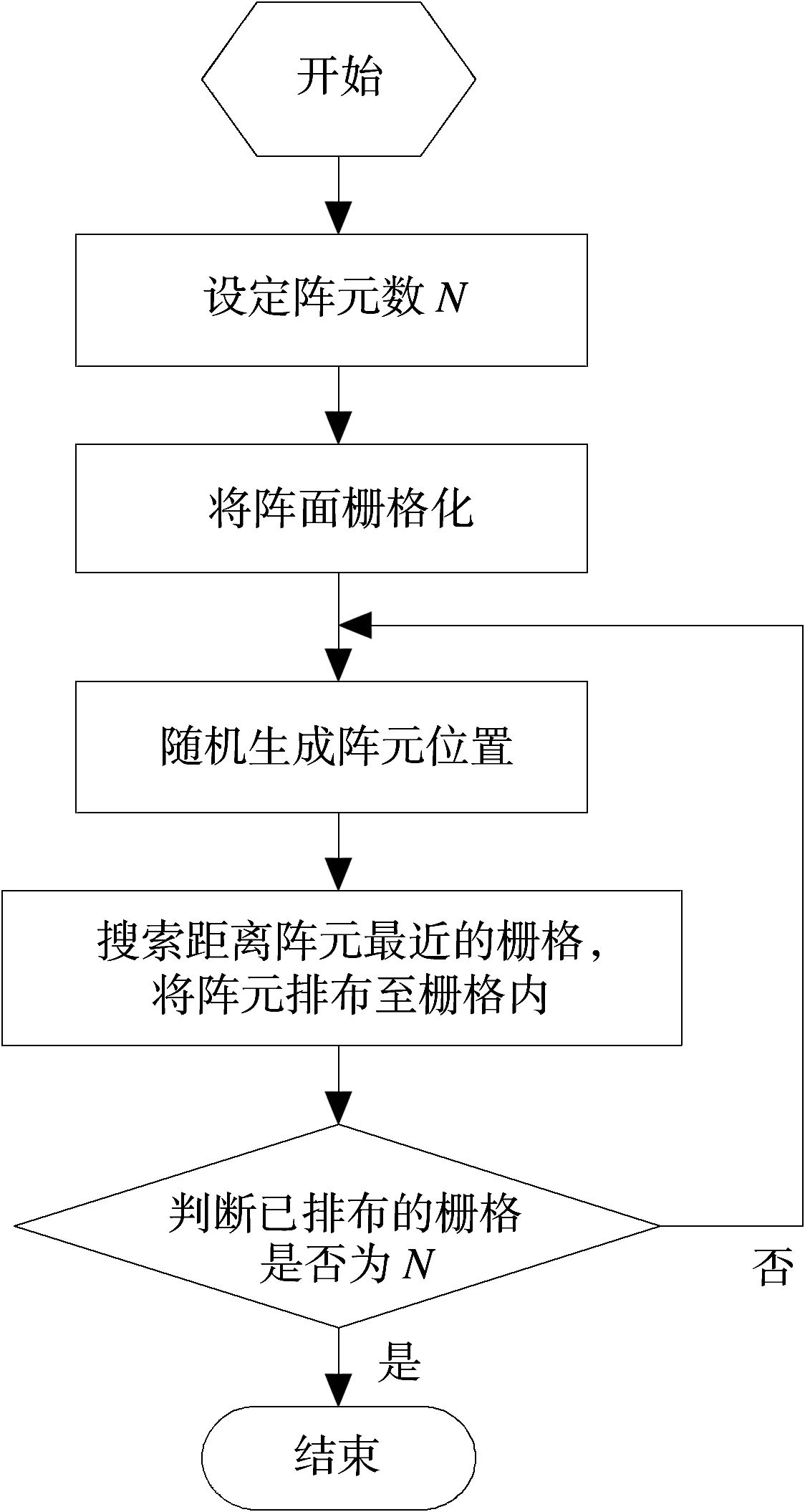
图2 排布方法流程框图

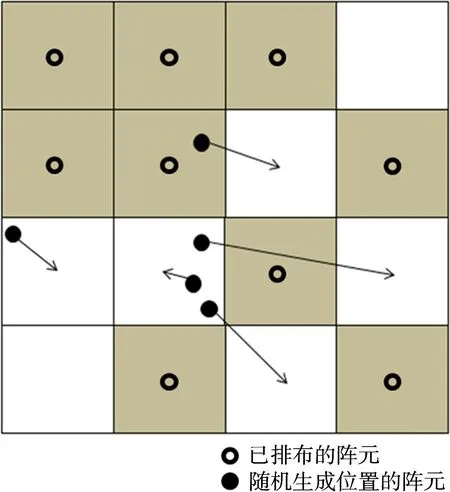
图3 阵元排布示意图

3 仿真验证

选择一个圆口径天线阵列进行分析,仿真验证的设计参数为:

天线口径:圆口径D=1.2 m

波长:λ=0.075 m

阵元最小间距:d=0.5λ

满阵阵元数:M=681

排布阵元数:N=256

阵面填充率:r=N/M=0.375

阵元位置的概率分布:高斯分布X～N(0, 64λ2/9),Y～N(0,64λ2/9)

密度加权阵所需的馈电幅度分布:A(x,y)为-30 dB的Taylor[6]分布。

3.1 天线阵面

因为高斯分布的阵元更加集中在阵面中心,有利于抑制旁瓣,所以阵元位置分布选择高斯分布。按照以上设计参数得到的天线阵面如图4所示,图中栅格代表可排布有源阵元的位置,共有681个。

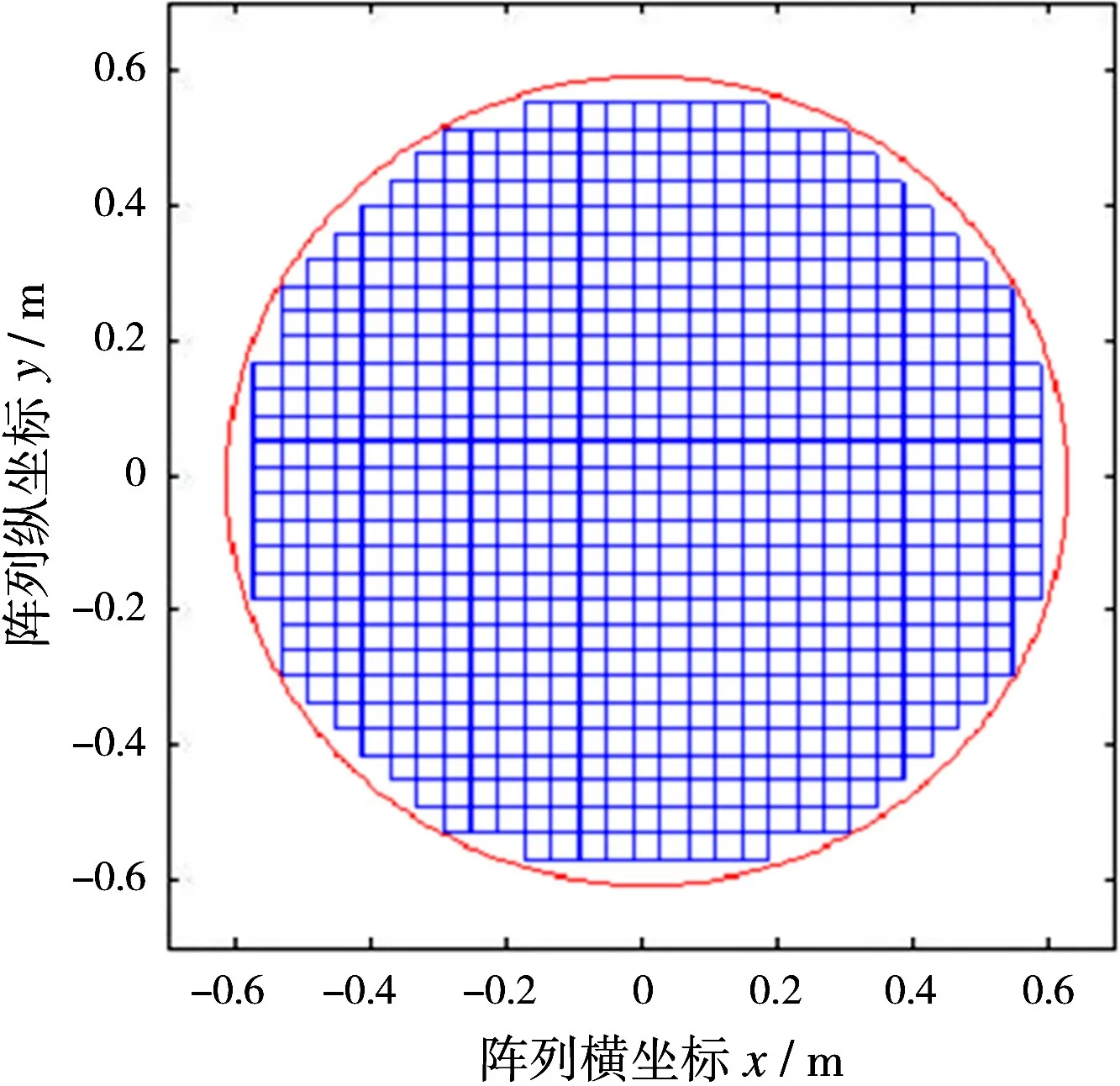
图4 天线阵面

3.2 阵元排布

根据上文分析的密度加权阵独立采样法和最短距离排布,得到两种排布方法的阵面,如图5、图6所示,图中“∗”代表排布的有源阵元。

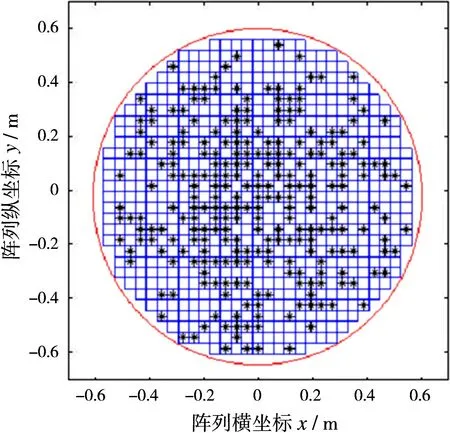
图5 密度加权阵

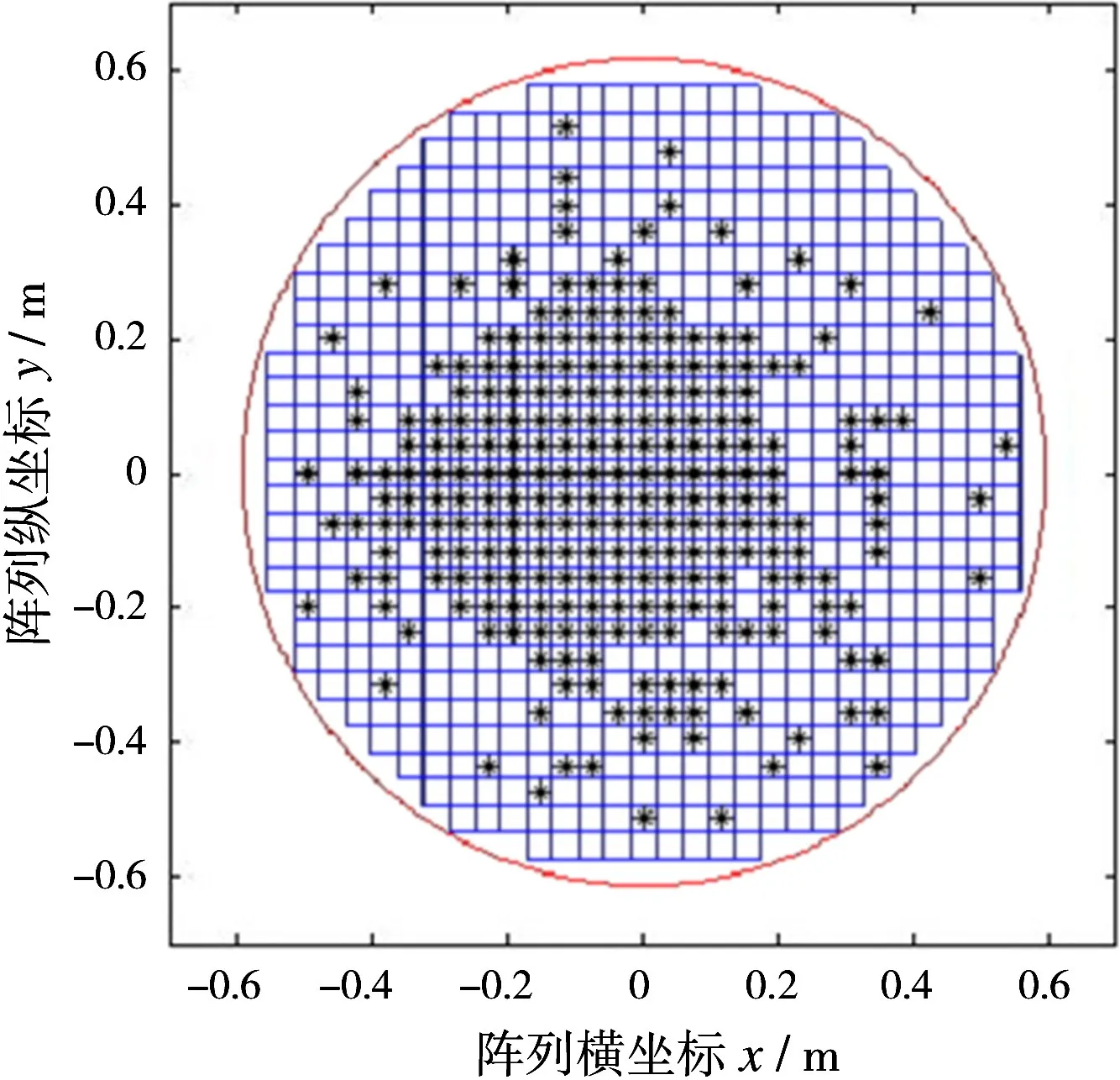
图6 随机圆口径阵(最短距离排布)

图中密度加权阵排布了259个阵元,最短距离排布的随机圆口径阵排布了256个阵元。从图5、图6中也可以看出,在高斯随机分布的基础上,最短距离排布的阵元在中心区域更加密集,有利于抑制旁瓣。

3.3 阵列的方向图

两种圆口径阵形成的方向图如图7、图8所示。

两种阵列方向图的最大旁瓣高度分别为-16.9 dB,-19.6 dB。

对于密度加权阵和随机阵,其阵元分布都不是唯一确定,即方向图是按照一定规律的随机。为了确定阵列方向图的性能,需要通过多次试验选出相对最优。通过50次试验得到各个阵列最大

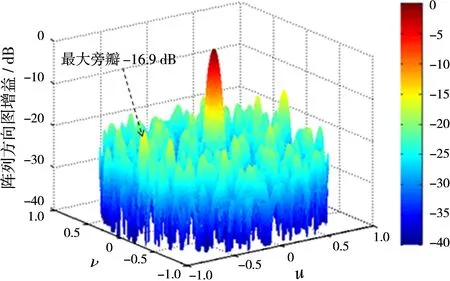
图7 密度加权阵方向图

图8 随机圆口径阵方向图(最短距离排布)

旁瓣高度最低的阵元排布,其方向图性能参数如表1所示。

表1 阵列主要性能参数对比

由表1可以看出,在抑制旁瓣方面,本文提出的最短距离排布具有更好的抑制旁瓣作用。在稀布256个阵元的条件下,填充率约为37.5%,其最大旁瓣高度能降低至-21 d B以下,相比密度加权阵有3 dB左右的改善。并且其增益更大,平均旁瓣更低。

表2给出了不同扫描角度下两种排布的阵列最大旁瓣高度,可以看出,在[-45°,+45°]扫描区间内,最短距离排布得到的随机圆口径阵在抑制旁瓣上优于密度加权阵。

表2 不同扫描角度方向图最大旁瓣高度

3.4 最大旁瓣高度与阵元数的关系

为了分析排布方法在不同稀疏程度下的抑制旁瓣效果,需要测量不同阵元数下的最大旁瓣高度。最大旁瓣高度随阵元填充率r变化如图9所示。其中最大旁瓣高度是30次试验中得到的最小值。

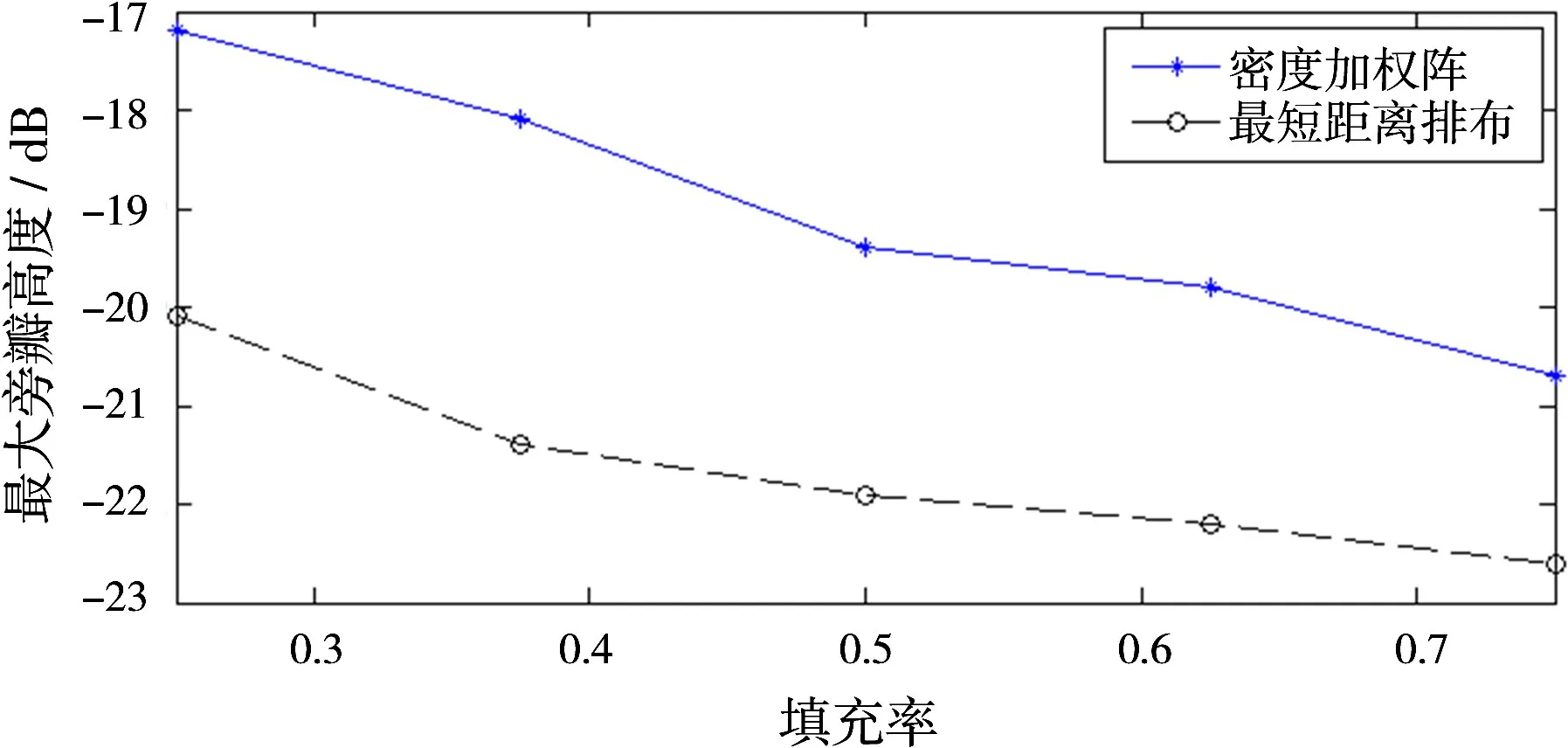
图9 不同填充率下的最大旁瓣高度

从图9可以看出,在不同的填充率下最短距离排布在降低旁瓣方面都优于密度加权阵,尤其是在低填充率下,最短距离排布的随机阵列优势更加明显。

3.5 小结

密度加权阵和随机阵都是阵元稀布的方法。密度加权阵的基础是幅度加权阵,先用幅度加权来控制方向图再用密度加权来实现阵元排布。虽然通过密度加权可以逼近幅度加权阵方向图,但此方法不能直接控制方向图。随机阵列则是基于方向图本身,通过概率密度函数和排布方法优化方向图,本文中在确定概率密度函数的基础上优化排布方法,提出的最短距离排布性能更好。由图9可知,最短距离排布的随机阵列在低填充率下抑制旁瓣具有明显的优势。另外,在控制阵元个数方面,密度加权阵只能根据预期的阵元数目来调节参数,最后得到的阵元数具有随机性,而本文中的最短距离排布能精确地控制阵元数量。

4 结束语

随机阵列中阵元位置的随机性使得在阵列稀布的情况下所形成的方向图不会存在栅瓣,但是传统的随机阵列理论只是对于随机阵列的各方面特性进行了研究,关于阵元排布等实际应用问题并没有过多考虑。

本文针对随机阵列的实际应用,考虑阵元在随机阵列理论基础上的排布问题,提出了一种随机阵列的最短距离排布方法。用这样的方法形成的随机阵列可以保证方向图的性能,同时减少了天线阵面中有源发射组件的使用,大大降低了成本。而相比于传统的独立采样密度加权阵列具有更好的抑制旁瓣效果,尤其关键的是这种方法更加简单易行,可以很好地应用到实际天线阵列当中。

[1]SKOLNIK M I,SHERMAN J III,OGG F Jr.Statistically Designed Density-Tapered Arrays[J].IEEE Trans on Antennas and Propagation,1964,12(4): 408-417.

[2]STEINBERG B D.Principles of Aperture and Array System Design:Including Random and Adaptive Arrays[M].New York:Wiley-Interscience,1976.

[3]JAYAPRAKASAM S,RAHIM S K A,LEOW C Y,et al.Genetic Algorithm Based Weight Optimization for Minimizing Sidelobes in Distributed Random Array Beamforming[C]∥International Conference on Parallel and Distributed Systems,Seoul:IEEE,2013:623-627.

[4]王华.基于统计相关理论和遗传算法的密度加权阵列天线改进设计和实践[D].南京:南京理工大学, 2008:11.

[5]BUCHANAN K,HUFF G H.Analysis and Experiments on Peaking Sidelobe and Scanning Behavior in Planar Random Arrays[C]∥Antennas and Propagation Society International Symposium,Memphis, TN:IEEE,2014:1369-1370.

[6]董鹏曙,金加根,谢幼才,等.天线副瓣对雷达探测的影响研究[J].雷达科学与技术,2014,12(1):112-115.

DONG Peng-shu,JIN Jia-gen,XIE You-cai,et al. Study on Influnce of Antenna Sidelobes on Radar Detection[J].Radar Science and Technology,2014,12 (1):112-115.(in Chinese)

[7]MAILLOUX R J.相控阵天线手册[M].南京电子技术研究所,译.北京:电子工业出版社,2007:39.

[8]钟顺平.天线理论与技术[M].北京:电子工业出版社,2011:56.

[9]蒋毅.天线阵列阵元位置优化方法研究[D].哈尔滨:哈尔滨工程大学,2013:3.

[10]黄飞,盛卫星,马晓峰.随机错位子阵阵列天线及其优化设计[J].电波科学学报,2008,23(5):917-921.

[11]李贺,赵飞,洪家财,等.密度加权的稀疏天线阵列研究[C]∥第十三届全国青年通信学术会议,烟台:中国通信学会,2008:706-709.