基于匹配傅里叶变换的相位解污染算法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

天波雷达向空中发射信号,信号经过电离层传播,电离层的不稳定性会对信号造成污染[1-4],其相位污染可以看作对回波信号的一个乘性调制。相位污染导致回波信号频谱展宽,在长相干积累下展宽更加严重,海杂波频谱扩展之后容易掩盖低速目标频谱[5-7],这对慢速舰船等低速目标的检测非常不利。因此电离层相位解污染是提高天波雷达目标检测能力的一个关键因素[8]。

关于天波雷达电离层相位解污染国内外有许多研究。

最大熵谱估计法(MESA)[9]将相位污染看作线性变换,采用MESA估计每段信号频率,然后通过内插估计污染函数,估计准确度不好。伪维格纳分布法(PWVD)[10]通过Wigner-Ville分布估计每个采样点的瞬时频率,在Bragg峰与相邻海杂波相互交叠引入交叉项的情况下,估计的瞬时频率效果不好。相位梯度法(PGA)[11]求取相邻采样点之间的相位梯度,累加得到相位污染函数。在噪声干扰比较严重时,扩展的Bragg峰在循环频移至零频时误差较大,且噪声相位也会产生较大的累积误差。多项式相位信号(PPS)[12-15]法直接估计污染函数相位,通过低阶多项式拟合回波信号,采用高阶模糊函数估计多项式各阶系数,该方法在存在交叉项时非常敏感,有待进一步改进。

为了避免交叉项的影响,Hankel降秩(HRR)[16]算法不需要滤出Bragg峰,利用回波信号进行污染估计,通过将回波信号折叠,构造一个Hankel矩阵,其本质是对信号进行分段,然后通过奇异值分解(SVD)估计回波瞬时频率,能获得较好的估计效果。该方法需要预先设定Hankel矩阵的列数和秩,即需要对回波中的信号成分有准确的先验知识,然而实际回波信号往往比较复杂,无法准确获得该先验知识,先验信息不足时估计效果不好。

基于上述考虑,本文提出一种基于匹配傅里叶变换的相位污染估计算法。该算法不需要已知回波的信号成分,采用三次相位函数分段拟合回波信号,再利用匹配傅里叶变换估计污染函数,结合各段污染函数即可进行解污染处理。由于实际回波中杂噪比高,算法受噪声相位扰动的影响小,该算法能够获得很好的估计效果。仿真结果表明,相比传统的HRR算法,本文算法不需要已知回波信号成分,而且具有更好的电离层相位解污染效果。

1 天波雷达回波信号模型

未受电离层相位污染的天波雷达回波信号可以表示为

式中,s(t)表示接收回波信号,其中包含海杂波c(t)、目标信号x(t)和噪声n(t)。回波中海杂波能量主要集中在±fb频率处,fb为海面被高频信号照射时形成的Bragg峰对应的频率值,fb的大小可以通过式(2)得到,式中g为重力加速度,f0为雷达工作频率,c为光速。

海杂波可以表示为式(3),式中B为海杂波幅度,fb为Bragg峰对应的频率值。

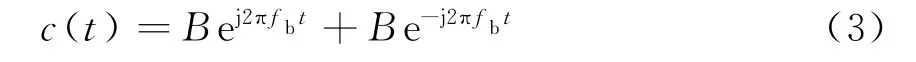
回波中匀速目标对应的回波信号可以表示为

式中,A为目标信号幅度,fa为匀速目标对应的多普勒频率,如式(5),f0为雷达工作频率,v为目标径向运动速度,c为光速。

根据上述海杂波和目标信号的表达式,接收回波可以进一步表示为

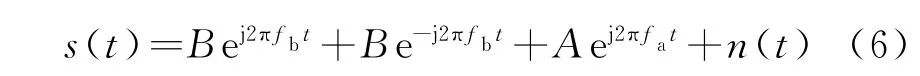
式(6)中未考虑电离层相位污染。由于天波雷达信号经过电离层反射传播,电离层的不稳定性会造成回波多普勒频率扩展。在信号处理中,电离层对回波造成的相位扰动可以建模为乘性干扰,不同的物理机制对应不同的污染函数。本文采用文献[16]中的相位污染函数,为一正弦污染函数,如式(7),式中M为相位污染的幅值,fm为相位污染的调制频率。

根据污染函数,将式(6)回波信号乘以相位扰动,即得到相位污染后的回波信号表达式:

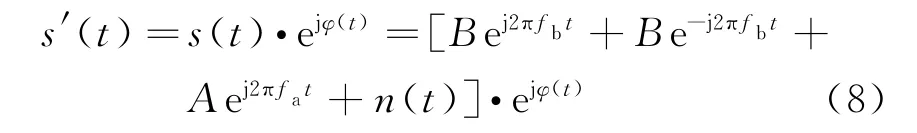
经过电离层相位污染的回波,信号频谱扩展,当目标多普勒频率与强大的Bragg峰频谱非常接近时,扩展后的海杂波信号将掩盖目标,导致低速目标的检测失效。在相干积累之前需要进行电离层相位解污染处理,抑制回波频谱扩展,减小电离层相位扰动的影响,下节详细介绍本文所提电离层相位解污染算法。

2 基于匹配傅里叶变换的电离层相位解污染算法

文献[16]中的HRR相位解污染算法需要已知回波中的信号成分,根据信号成分设定Hankel矩阵的列数和秩,而实际工程中很难准确获得该先验信息。本文提出一种新的电离层相位污染估计算法,不需要已知该先验信息。本文算法采用三次相位函数对回波信号分段拟合,然后基于匹配傅里叶变换估计污染函数。由于回波中海杂波能量很强,杂噪比高,该算法受噪声相位扰动影响小,估计精度高,污染校正效果好。

在估计污染函数前,在频域上滤出单个Bragg峰,然后进行IFFT转化为时域信号,这里采用负Bragg峰,分析可知该信号表达式如式(9):

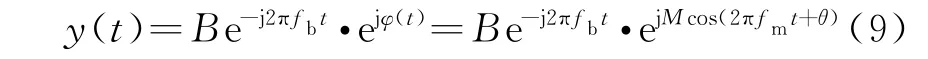
信号y(t)的瞬时频率如式(10)所示:

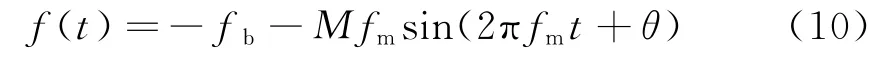
在回波信号受到相位污染较严重的情况下,回波信号相位波动较大。为了提高估计精度,本文将回波信号分成若干段,采用三次相位函数拟合每小段回波信号,假设任意段信号y(t)的离散表达式为

式中,Y为信号幅度,a0,a1,a2,a3为对应各阶相位系数。对回波信号y(n)定义如下运算算子:

为了保证运算算子中n+l和n-l均有意义,需满足1≤n+l且n-l≤N这一条件,N为信号的长度。

回波信号经过上述运算算子处理之后,若将n看作定值,l看作变量,则运算后将三次相位函数转化为二次相位函数。然后对该二次相位函数进行匹配傅里叶变换,如式(13):

根据式(13)可知,匹配傅里叶变换之后得到一个关于α的函数,该函数在α=2a2+6na3时取最大值。分别取两点n1和n2,求出函数MFT(α,n)的最大值,然后求取其对应的α,假设分别为α1和α2,如式(14)、(15):

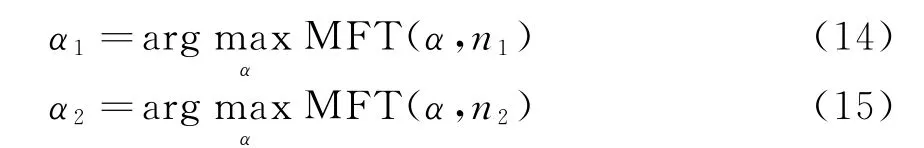
通过式(14)、(15)和式(13)得到α1和α2。同时根据理论推导,α1和α2分别满足式(16)和式(17):

将上式写成方程组,如式(18):

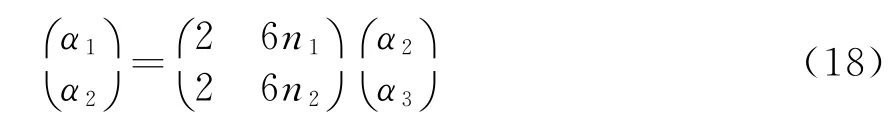
通过a2和a3的估计值,构建频率补偿因子,将回波信号乘以该补偿因子,对回波信号进行相位补偿,如式(20):

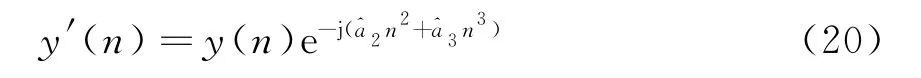
补偿后的回波信号y′(n)为一单频信号,FFT将信号转化为频率域,取最大值对应的频率值,估计a1,如式(21):

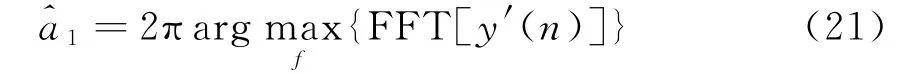
吃早点时，一直打听，早年间，吉和街那家著名锅贴饺的去处，早已不知所踪，唯有天主教堂犹在，雁青色的细砖外围，哥特式尖顶，高高耸立于吉和街。弟弟妹妹上学的吉和街小学也不见了。

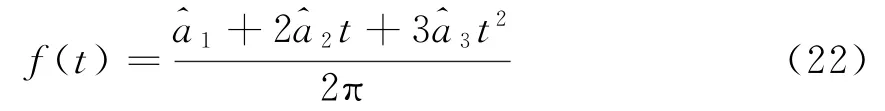
将估计的瞬时频率值f(t)减去理论的Bragg峰频率fb,则得到估计的污染函数瞬时频率。

将污染函数的频率值积分,变换成污染相位,然后进行电离层相位解污染。将受电离层污染的回波信号s′(t)乘以估计的相位污染函数的共轭,即可完成电离层相位解污染,如式(23)所示:

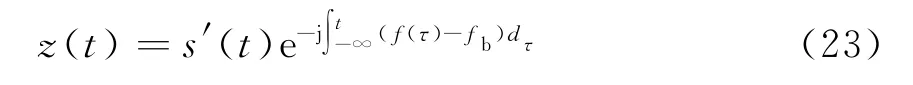
式中,z(t)为解相位污染之后的回波信号,s′(t)为原始的受电离层污染的回波信号,f(τ)-fb为估计的污染函数瞬时频率值。

3 仿真结果及分析

本文利用三次相位函数对回波信号进行分段拟合,然后基于匹配傅里叶变换估计污染函数。由于回波中海杂波能量很强,回波杂噪比高,本文算法能够准确地估计污染函数,并且不需要已知回波信号成分。

由于实际回波的复杂性,本文算法应用于实际回波处理还需要进一步研究。目标处于Bragg峰的位置会导致估计不准确,因为该算法需要提取单个Rragg峰。本文算法估计相位污染函数时不需要目标信号信息,在目标为非匀速的情况下仍然试用。以下仿真中的匀速目标位置不在Bragg峰内。

图1是相位污染前的回波频谱。在频率轴上存在对称的正负Bragg峰,回波中海杂波能量最大,因此Bragg峰的幅值在回波频谱中最高。在正Bragg峰右边存在一个较强的小尖峰,代表一匀速目标。由于未受电离层相位污染,回波频谱没有扩展,海杂波Bragg峰与低速目标频谱是分开的,可以检测出目标。工程实际中,由于存在电离层相位污染,回波频谱存在扩展,如图2所示。

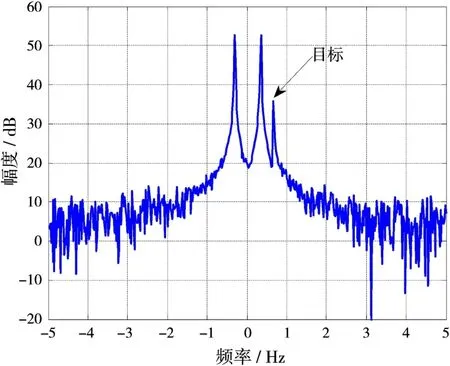
图1 相位污染前的回波信号频谱图

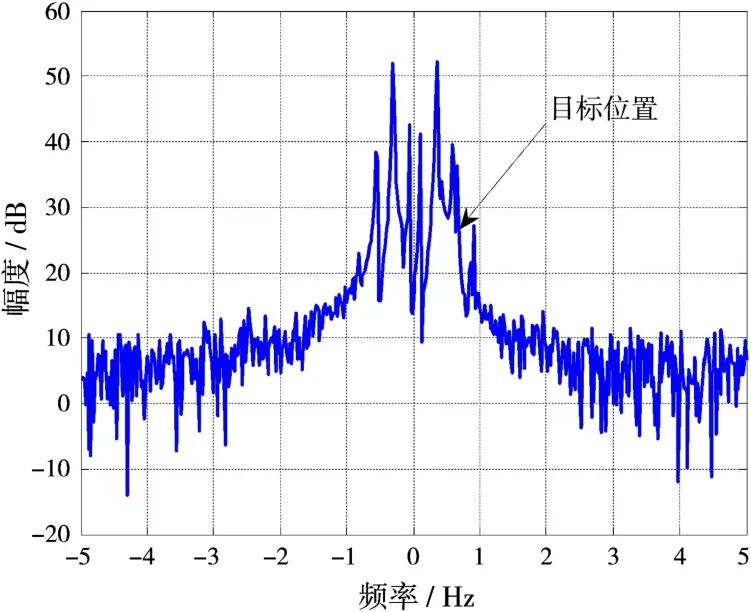
图2 相位污染后的回波信号频谱图

图2是受电离层相位污染之后的回波频谱,电离层的相位污染相当于对回波进行相位调制,导致回波多普勒频谱展宽,其中海杂波强大的Bragg峰扩展后,掩盖靠近海杂波频谱的低速目标,导致无法检测低速目标。在目标检测之前需进行电离层相位解污染,抑制回波的频谱扩展。

图3和图4为相位解污染之后的回波频谱图,图3是本文算法解相位污染之后的回波频谱。相比解污染之前,海杂波Bragg峰和目标频谱均得到极大的锐化,解污染后,回波频谱扩展得到抑制,将掩盖在Bragg峰中的目标分离出来,可以清楚地检测出目标。为了对比分析,图4为在相同条件下传统HRR算法解相位污染结果,在回波信号成分这一先验信息不足时,相比解污染之前,海杂波Bragg峰得到了一定的锐化,但是目标信号仍然无法与海杂波Bragg峰分离,无法检测目标。对比图3和图4可以得出,本文算法不需要已知回波信号成分这一先验信息,而且能够得到更准确的污染函数,具有更好的解污染效果。

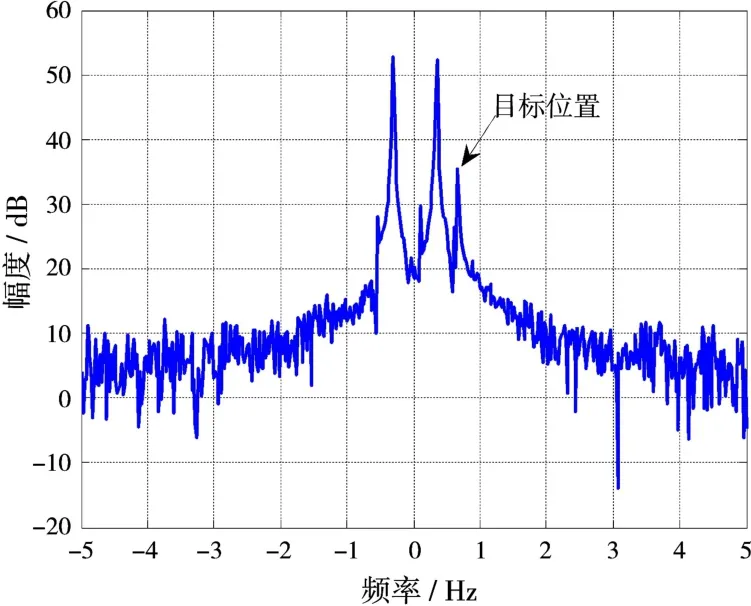
图3 本文算法解污染后回波频谱图

图4 HRR算法解污染后回波频谱图

4 结束语

本文注意到回波中杂噪比高,利用三次相位函数分段拟合回波信号,采用基于匹配傅里叶变换的方法估计污染函数,能够得到准确的污染函数。为了提高估计准确度,采用数据重用方法,利用估计出的相位污染函数对原始回波进行相位解污染处理。解相位污染之前强大的海杂波Bragg峰扩展严重,掩盖了靠近海杂波并且能量相对较弱的低速目标。解相位污染之后,海杂波频谱得到锐化,将目标从海杂波中提取出来。仿真结果表明,相比已提出的HRR算法,本文算法不需要已知回波信号成分,能够得到更准确的污染函数,具有更好的解相位污染效果。

[1]周万幸.天波超视距雷达发展综述[J].电子学报,2011,39(6):1373-1378.

[2]罗欢,陈建文.天波超视距雷达电离层相位污染典型校正方法综合性能评估[J].宇航学报,2013,34(2):262-269.

[3]戴文娟,胡进峰,肖赛军,等.基于遗传算法的OTHR机动弱目标检测[J].雷达科学与技术,2013,11(1):59-64.

DAI Wen-juan,HU Jin-feng,XIAO Sai-jun,et al.Maneuvering Weak Target Detection Based on Genetic Algorithm for OTH Radar[J].Radar Science and Technology,2013,11(1):59-64.(in Chinese)

[4]赵晓燕,于长军,陈磊.基于改进的小波-矩阵法实现雷电干扰抑制[J].雷达科学与技术,2013,11(4):401-408.

ZHAO Xiao-yan,YU Chang-jun,CHEN Lei.Lightning Interference Suppression Based on Improved Wavelet-Matrix Combined Algorithm[J].Radar Science and Technology,2013,11(4):401-408.(in Chinese)

[5]韩卫国,徐晋,付启众.分数阶包络补偿在稀布阵雷达中的应用[J].雷达科学与技术,2012,10(3):267-271.

HAN Wei-guo,XU Jin,FU Qi-zhong.Application of Fractional Order Motion Compensation in Synthetic Impulse and Aperture Radar[J].Radar Science and Technology,2012,10(3):267-271.(in Chinese)

[6]杨雪亚,杨广玉.基于稀疏解的米波雷达测高方法[J].雷达科学与技术,2012,10(6):629-632.

YANG Xue-ya,YANG Guang-yu.Method of Height Measuring Based on Sparse Solution in Meter Wave Radar[J].Radar Science and Technology,2012,10(6):629-632.(in Chinese)

[7]陈文涛,马子龙,周必全.高频地波雷达系统优化控制的研究与建模[J].雷达科学与技术,2014,12(1):13-19.

CHEN Wen-tao,MA Zi-long,ZHOU Bi-quan.Research and Modeling of Performance Evaluation and Optimizing Control in High Frequency Surface Wave Radar[J].Radar Science and Technology,2014,12(1):13-19.(in Chinese)

[8]薛峰,谢谠,陈辉.天波超视距雷达窄带干扰抑制技术研究[J].雷达科学与技术,2009,7(3):163-168.

XUE Feng,XIE Dang,CHEN Hui.Study on Narrowband Interference Suppression in Sky Wave OTHR[J].Radar Science and Technology,2009,7(3):163-168.(in Chinese)

[9]BOURDILLON A,GAUTHIER F,PARENT J.Use of Maximum Entropy Spectral Analysis to Improve Ship Detection by Over-the-Horizon Radar[J].Radio Science,1987,22(2):313-320.

[10]HOWLAND P E,COOPER D C.Use of the Wigner-Ville Distribution to Compensate for Ionospheric Layer Movement in High-Frequency Sky-Wave Radar Systems[J].IEE Proceedings,Part F:Radar and Signal Processing,1993,140(1):29-36.

[11]邢孟道,保铮.电离层电波传播相位污染校正[J].电波科学学报,2002,17(2):129-133.

[12]LU K,WANG J,LIU X Z.A Piecewise Parametric Method Based on Polynomial Phase Model to Compensate Ionospheric Phase Contamination[C]∥2003 IEEE International Conference on Acoustics,Speech,and Signal Processing,Hongkong:IEEE,2003:405-408.

[13]姜维,邓维波.分段多项式建模校正电离层相位污染算法研究[J].电波科学学报,2011,26(5):855-863.

[14]游伟,何子述,陈绪元,等.基于三次相位建模的天波雷达污染校正[J].电波科学学报,2012,27(5):875-879.

[15]刘颜回,聂在平,赵志钦.改进的分段多项式建模的电离层相位去污染新方法[J].电波科学学报,2008,23(3):476-483.

[16]LU K,LIU X Z,LIU Y T.Ionospheric Decontamination and Sea Clutter Suppression for HF Skywave Radars[J].IEEE Journal of Oceanic Engineering,2005,30(2):455-462.