采用拟静力法的新型桶式基础防波堤结构稳定性分析
杨立功
(1.同济大学 地下建筑与工程系,上海 200092;2.南京水利科学研究院,江苏 南京 210029)
采用拟静力法的新型桶式基础防波堤结构稳定性分析
杨立功1,2
(1.同济大学 地下建筑与工程系,上海 200092;2.南京水利科学研究院,江苏 南京 210029)
三维情况下,桶体稳定性是一个复杂的空间结构与土相互作用的问题。结合工程实例,建立了三维新型桶式基础防波堤有限元模型,对其稳定性进行分析。从而,动力作用下桶体结构位移与目前静力计算的结果相差较大,针对这个问题,分析提出等效拟静力法,通过与动力作用后相等的孔压等效成与之对应的静荷载,然后计算桶体位移。该方法的关键是找出桶体前端底部土体孔压与静荷载之间的关系,同时找出此处土体孔压与动荷载之间的关系,从而建立静荷载与动荷载之间的关系。经数值模拟与试验对比,结果证明所提的等效拟静力法比较合理。在模拟与分析原型桶体基础上,进一步分析了不同尺度及不同荷载作用点高度时,桶体前端底部土体孔压与静荷载之间的近似直线关系。
新型桶式基础防波堤;稳定性;静荷载;动荷载;等效拟静力法
杨立功.采用拟静力法的新型桶式基础防波堤结构稳定性分析[J].水利水运工程学报,2015(5):96-102.(YANG Li⁃gong. Stability analysis of new bucket foundation breakwater structure based on quasi⁃static method[J].Hydro⁃Science and Engineering,2015(5):96-102.)
随着传统防波堤结构在大型、新型港口建设中的应用受到不同程度的制约,新型桶式基础防波堤结构开始应用于港口防波堤工程中。沉入较深土层的这种新型桶式结构,无需对地基进行加固处理,靠桶体自重、桶壁、桶底与其外侧土体的协同工作来抵抗外力,也就是通过土体的嵌固作用来维持其稳定性。
目前一些学者对防波堤结构稳定性做了不少研究。范庆来[1-2]利用ABAQUS有限元软件,采用线弹性模型、Duncan⁃Chang模型对软土地基上深埋式大圆筒结构的极限承载力进行了拟静力分析。陈福全等[3]利用三维有限元采用D⁃P模型对一实际工程采用的大圆筒码头结构进行分析,研究了大直径圆筒码头的工作性状。王刚等[4]利用有限元软件MARC采用Mohr⁃Coulomb模型对单筒和圆筒墙进行了有限元分析。武科等[5]基于大型有限元分析软件ABAQUS,采用理想弹塑性模型,考察了不同荷载组合加载模式下桶形基础破坏包络面形状,并给出了其数学表达式。孙曦源等[6]同样采用理想弹塑性模型,探讨了饱和软黏土地基中单桶基础水平承载力的工作特性。王元战等[7]采用D⁃P模型对筒型基础防波堤进行了有限元分析,通过分析得出了其失稳模式,并建立了基于实际转动点的结构稳定性计算方法。李武等[8]利用PLAXIX有限元软件,采用Mohr⁃Coulomb模型对带隔舱的桶式基础防波堤进行了三维有限元分析,探讨了土体参数、桶体埋深对桶体稳定性的影响。肖忠等[9]采用D⁃P模型对筒型基础防波堤进行了数值分析,提出了桶体稳定性的4个判别标准。
上述研究采用拟静力法、基于有限元软件的数值方法对大圆筒、箱筒、隔舱桶等结构与土的相互作用进行了探讨,分析了土中结构物的稳定性。在上述分析过程中:首先,土体本构模型基本上为弹性模型、理想弹塑性模型,这些模型难以反映软土地基上土的真实应力-应变状态;其次,均未考虑孔隙水对结构物稳定性的影响;最后,采用拟静力法时所施加的荷载实际上是极限条件下的持续静荷载,与结构所承受的循环动荷载有所不同。针对以上研究中的不足,本文采用能反映土体非线性、非弹性、塑性体应变、塑性剪应变及应变硬化与软化特性的南水模型,同时考虑孔压影响,采用等效拟静力法,将实际条件下动荷载作用时土体孔压上升稳定后对应的波浪动荷载转换成相等孔压条件下对应的静荷载,初步探讨新型桶式基础防波堤的稳定性。
1 新型防波堤结构型式
新型桶式防波堤单桶由上部两个等直径小圆桶、下部带9个隔舱的1个近似大椭圆桶组合而成(如图1)。这种防波堤结构为钢筋混凝土结构,先在岸上进行单桶预制,待整个单桶结构预制完成后浮运至沉降点进行负压下沉,单桶的长轴方向为海测-港侧方向,短轴方向为整个防波堤走向。建成后,下桶在土内,控制着整个桶体稳定性,上桶部分在海水中,承受水平波浪荷载。

图1 沉入式新型桶式基础防波堤结构Fig.1 A new embedded bucket foundation breakwater
2 有限元模型的建立
南京水科院沈珠江院士等(1985)提出的双屈服面弹塑性模型,服从广义塑性力学理论。该模型把屈服面看作弹性区域的边界,采用塑性系数代替传统的硬化参数。模型有10个参数(见表1),全部可通过三轴排水试验获得。

表1 各土层土性参数Tab.1 Parameters of soil layers
地基土分两层,上层为淤泥,厚9.5 m,饱和密度1.68 kg/m3,初始孔隙比1.819,渗透系数2×10-10m/s,静止侧压力系数0.885;下层为粉质黏土,厚24.5 m,饱和密度1.92 kg/m3,初始孔隙比为0.77,渗透系数为6× 10-9m/s,静止侧压力系数0.7。
桶体采用线弹性本构模型,上桶高为12 m,下桶高为11 m,下桶底端嵌入粉质黏土层1.5 m。采用50年一遇波浪荷载,模型荷载采用与波浪合力等效的集中荷载,作用在上桶桶壁,作用点距上桶底端6 m。
模型采用双面排水:模型土体的上表面和下表面。桶体与土体之间采用Mohr⁃Coulomb摩擦,摩擦系数取0.115。建立的桶体模型如图2所示。

图2 桶式基础防波堤有限元模型Fig.2 A finite elementmodel for a bucket foundation breakwater
3 计算结果分析
在水平波浪荷载作用下,桶体发生由海侧向陆侧的水平位移、竖向沉降及转动。为方便起见,取下桶盖板中心的水平位移、下桶陆侧端头的竖向位移及桶体转角进行分析,不同荷载水平P/PPP及不同孔压条件下的位移及转角如图3和4所示。由图3可见,荷载水平越高,桶体位移越大,而且在孔压作用下,桶体位移稳定所需时间越长。由图4可见,考虑孔压与不考虑孔压的最终计算位移十分接近,但如果考虑固结时间,桶体在不同时期的位移不同。

图3 不同荷载水平下桶盖板中心水平位移和桶体最大竖向位移Fig.3 Horizontal displacement of cover board centre and maximum vertical displacement of bucket under different loads
图4(a)中离心机试验位移[10]在P/PPP≤1.0时,与数值模拟中初始加载时的位移比较接近,当P/PPP≥1.0时,试验位移大于数值模拟中的初始加载位移,这是由于离心机试验中,随着加载时间延长,桶体周围土体固结所致。图4(b)和(c)中离心机试验竖向位移及转角[10]由测点位移转换成桶端最大位移及转角,此处试验位移与数值模拟位移相差稍微大一些,但位移与荷载变化趋势一致。

图4 不同孔压条件下桶体盖板中心水平位移、桶体最大竖向位移和桶体转角Fig.4 Horizontal displacement of cover board centre,maximum vertical displacement and turn angle of foundation bucket under different pore pressures
实际情况下防波堤桶体所承受的波浪荷载并非是持续不变的极端海况下的荷载,因此,不考虑孔压所计算的位移实际上是极端荷载作用下孔压消散完后的最终位移,这与实际情况不符。这时计算的桶体位移远大于桶体的实际位移,如图4(a)和(b)所示。如按承载力定义桶体的安全系数,不考虑孔压,P/PPP≤1时,荷载-位移曲线接近直线,P/PPP≥1.2时,荷载-位移曲线的曲率明显增大,此时取桶体的安全系数为1.2。如果考虑孔压影响,此时桶体有更大的安全储备。
桶体刚施加水平波浪荷载P时(图5),桶体椭圆前端底部O点的超孔压随荷载水平变化如图6所示。从图6可见,此处超孔压与荷载水平大致呈线性关系。

图5 桶体与土体受荷模型Fig.5 A model for soil and bucket bearing load

图6 不同荷载水平下下桶前端底部孔压响应Fig.6 Bottom pore pressure response of front end of bucket under different loads
4 考虑孔压影响的桶体稳定性
动荷载作用时土体内孔压会上升,在波浪循环荷载作用下,假定O点的动孔压上升值为ud,静荷载P作用下O点的超孔压为u,则根据图6与动孔压ud对应的等效拟静力荷载Psd为:,其中:ub为桶体自重产生的超孔压。
根据循环三轴试验,设定与桶体椭圆端底部土体相同的固结应力条件,可弄清此处动孔压的发展模式并找出该处动孔压,利用上式可算出其对应的等效拟静力荷载,然后将此荷载代替动力荷载进行桶体稳定性计算。
李武[10]研究桶体稳定性时,进行了竖向固结应力150 kPa,侧向固结应力100 kPa,轴向循环应力30 kPa,循环周期9 s的动三轴土体特性试验,与本文数值模型计算中P/PPP=0.4时的情况类似。P/PPP=0.4时,无孔压条件下σ1=136 kPa,σ3=94 kPa,由波浪荷载P/PPP=1产生的循环轴向应力的拟静力为30 kPa,计算结果如图4所示。
离心试验时[10],盖板中心水平位移u1,桶体平均竖向位移u3和桶体转角θ分别为28 mm,77 mm和0.059°;不考虑孔压时,三者分别为133 mm,55 mm和0.428°;考虑孔压时,三者分别为48 mm,52 mm和0.057°。可见,考虑动孔压影响的等效拟静力计算方法比不考虑孔压影响的纯有效应力计算方法更接近离心机动力模型试验结果。此计算结果的转角很小,只有0.057°,而下桶盖板中心的水平位移为48 mm,桶体发生了较大水平位移。因此,桶体稳定性以控制水平位移为主,这也可以从图7中看出,整个加载过程中,水平位移与其控制值的比值大于转角与其位移控制值的比值。图7中,C/[C]表示位移实际值与控制值的比值,本文中桶体水平位移控制值为80 mm,转角控制值为0.458°;ρ1=u1/[u1],ρ2=θ/[θ]。
桶体底部水平位移控制着桶体的滑动。从图8桶体底部水平位移变化中可见,当荷载水平P/PPP≤1时,即50年一遇的波浪荷载条件下,桶体位移小于0.05 m,如按前述的等效拟静力分析方法,动力作用下桶体底部位移小于0.02 m。P/PPP≤1.2时,桶底两端水平位移相差不大,P/PPP>1.2时,桶体底部位移加速,且桶体前后端的水平位移差值逐渐增大。表明在50年一遇波浪荷载条件下,桶体的整体变形以滑移为主。

图7 不同荷载水平下桶体位移与控制值的比值Fig.7 Ratios between real displacement and control displacement under different loads

图8 桶体底部水平位移Fig.8 Bottom horizontal displacement of foundation bucket
5 其他情况下的桶体稳定性及土体孔压响应
5.1 桶体尺度变化
取原型桶体、尺度为原型1/2倍桶体、尺度为原型1/4倍桶体分别进行计算,桶体转角如图9所示。原型桶体所施加的荷载为PPP,桶体缩小时,所施加的荷载分别为PPP/4和PPP/64。相同荷载水平下,桶体尺寸越大,桶体转角越大。桶体尺寸变化时,桶体前端底部土体孔压响应如图10所示。不同尺寸的桶体,桶体前端底部土体孔压响应与荷载水平大致呈线性变化。

图9 不同荷载水平下不同尺寸的桶体转角Fig.9 Turn angle of bucket having various sizes under different loads

图10 不同桶体尺寸时下桶前端底部孔压响应Fig.10 Bottom pore pressure response of front end of bucket during variation in size of foundation bucket
5.2 荷载作用点高度变化
荷载水平P/PPP=1时,取荷载作用点位置分别为距离下桶盖板顶部2,4,6,8,10和12m进行计算,桶体转角如图11所示。桶体转角随荷载作用点高度增大而增大,当h≥6 m时,桶体转角变化加剧。
桶体前端底部土体随荷载作用点高度变化时的孔压响应见图12,荷载作用点高度h≤8 m时,孔压与荷载作用点高度之间呈线性变化,h>8 m时,孔压与荷载作用点高度之间也呈线性变化,但直线斜率稍微增大。
不同荷载作用高度下,桶体水平位移值、转角值分别与其控制值比值的变化见图13。在不同荷载作用高度下,桶体水平位移与其控制值的比值u1/[u1]均大于桶体转角与其控制值的比值θ/[θ]。桶体稳定性应以控制桶体水平位移为主。但荷载作用点位置较高时,桶体转角加剧,此时桶体滑移与倾覆均需要重点考虑。

图11 荷载作用点高度变换时的桶体转角Fig.11 Turn angle of bucket under different heights of load application points

图12 荷载作用高度变化时下桶前端底部孔压响应Fig.12 Bottom pore pressure response of front end of bucket under different heights of load application points
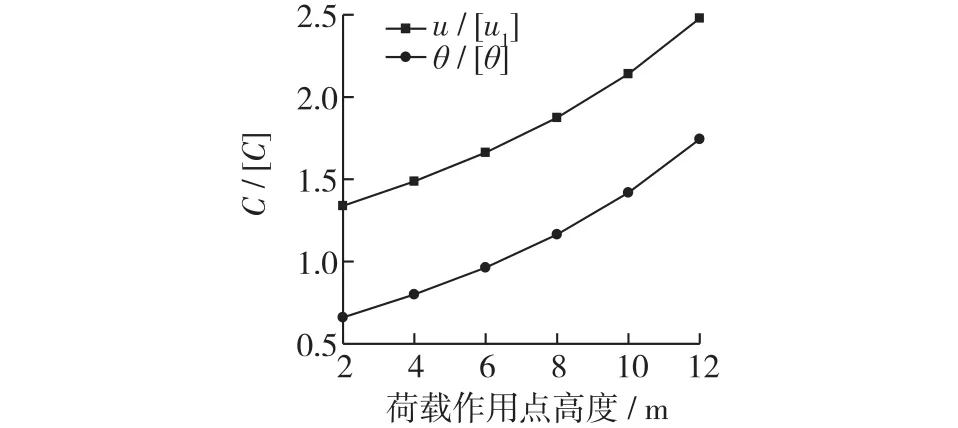
图13 不同荷载作用高度桶体位移与控制值的比值Fig.13 Ratios between real displacement and control displace⁃ment under heights of load application points
6 结 语
(1)考虑孔压的桶体最终变形与不考虑孔压按有效应力法计算的最终变形一致。
(2)动力作用下,桶体周围土体的孔压会上升,土体会弱化,但积累到一定程度后稳定,按照这个条件进行等效拟静力计算的桶体位移与真实情况较为接近。
(3)由于桶式基础防波堤对水平位移的控制较为严格,对桶体稳定性以控制水平位移为主。
(4)不同桶体尺度、不同荷载作用点高度下,桶体前端底部桶体孔压与荷载均呈近似直线关系。相同荷载水平下,桶体尺度小、荷载作用点低,桶体稳定性好。
[1]范庆来.软土地基上深埋式大圆筒结构稳定性研究[D].大连:大连理工大学,2005.(FAN Qing⁃lai.A study of stability deeply embedded large⁃diameter cylindrical structure in soft ground[D].Dalian:Dalian University of Technology,2005.(in Chinese))
[2]范庆来,栾茂田,杨庆,等.考虑循环软化效应的软基上深埋大圆筒结构承载力分析[J].大连理工大学学报,2006,46(5):702⁃706.(FAN Qing⁃lai,LUAN Mao⁃tian,YANG Qing.Analyses of bearing capacity for deeply⁃buried large⁃diameter cylindrical structure on soft clay considering cyclic⁃softening effect[J].Journal of Dalian University of Technology,2006,46(5):702⁃706.(in Chinese))
[3]陈福全,杨敏.大直径圆筒结构码头性状分析[J].同济大学学报,2002,30(7):797⁃801.(CHEN Fu⁃quan,YANGMing. Numerical analysis ofbehavior of large diameter cylindricalwharf structure[J].Journalof TongjiUniversity,2002,30(7):797⁃801.(in Chinese))
[4]王刚,陈杨,张建民.大圆筒结构倾覆稳定分析的有限元法[J].岩土力学,2006,27(2):238⁃241.(WANGGang,CHEN Yang,ZHANG Jian⁃min.A finite elementmethod for analyzing overturn stability of large cylindrical structures[J].Rock and Soil Mechanics,2006,27(2):238⁃241.(in Chinese))
[5]武科,栾茂田.复合加载模式下桶形基础破坏包络面弹塑性有限元数值分析[J].工程力学,2008,25(11):156⁃161.(WU Ke,LUAN Mao⁃tian.Numerical analysis of failure envelopes of bucket foundation subjected to combined loads based on elasto⁃plastic FEM[J].Engineering Mechanics,2008,25(11):156⁃161.(in Chinese))
[6]孙曦源,栾茂田,唐小微.饱和软黏土地基中单桶形基础水平承载特性有限元研究[J].大连理工大学学报,2010,50(5):702⁃707.(SUN Xi⁃yuan,LUAN Mao⁃tian,TANG Xiao⁃wei.Finite element study of horizontal bearing characteristics of single⁃bucket foundation on saturated soft clay ground[J].Journal of Dalian University of Technology,2010,50(5):702⁃707.(in Chinese))
[7]王元战,肖忠.筒型基础防波堤稳定性简化计算方法[J].岩土力学,2009,30(5):1 367⁃1 372.(WANGYuan⁃zhan,XIAO Zhong.A simplified calculation method for stability of bucket foundation breakwater[J].Rock and Soil Mechanics,2009,30(5):1 367⁃1 372.(in Chinese))
[8]李武,陈甦,程泽坤,等.水平荷载作用下桶式基础结构稳定性研究[J].中国港湾建设,2012(5):14⁃18.(LIWu,CHEN Su,CHENG Ze⁃kun.Stability study of bucket⁃based structure on horizontal loading[J].China Harbour Engineering,2012(5):14⁃18.(in Chinese))
[9]肖忠,王元战,及春林,等.筒型基础防波堤稳定性有限元数值分析[J].土木工程学报,2009,42(7):119⁃125.(XIAO Zhong,WANG Yuan⁃zhan,JIChun⁃lin,etal.Finite elementanalysis of the stability of bucket foundation breakwater[J].China Civil Engineering Journal,2009,42(7):119⁃125.(in Chinese))
[10]李武.新型桶式基础防波堤与地基动力相互作用研究[D].南京:南京水利科学研究院,2014.(LIWu.Research of interaction between new bucket⁃based structure and ground in dynamic loading[D].Nanjing:Nanjing Hydraulic Research Institute,2014.(in Chinese))
[11]胡中雄.土力学与环境土工学[M].上海:同济大学出版社,1997.(HU Zhong⁃xiong.Soil mechanics and environment geotechnics[M].Shanghai:Tongji University Press,1997.(in Chinese))
[12]王元战,肖忠,李元音,等.筒型基础防波堤土压力性状的有限元分析[J].岩土工程学报,2009,31(4):622⁃627.(WANG Yuan⁃zhan,XIAO Zhong,LI Yuan⁃yin,et al.Finite element analysis for earth pressure on bucket foundation ofbreakwater[J].Chinese Journal of Geotechnical Engineering,2009,31(4):622⁃627.(in Chinese))
[13]蒋敏敏,蔡正银,肖昭然.箱筒型基础防波堤基础筒土压力数值模拟研究[J].水运工程,2012(3):20⁃23.(JIANG Min⁃min,CAI Zheng⁃yin,XIAO Zhao⁃ran.Numerical study on earth pressure on foundation bucket of bucket foundation breakwater[J].Port&Waterway Engineering,2012(3):20⁃23.(in Chinese))
Stability analysis of new bucket foundation breakwater structure based on quasi⁃static method
YANG Li⁃gong1,2
(1.Department ofGeotechnical Engineering,Tongji University,Shanghai 200092,China;2.Nanjing Hydraulic Research Institue,Nanjing 210029,China)
Under the conditions of three dimensions,the stability of a bucket is one of the complex stability problems of the interaction between dimensional structures and soilmass.Based on case studies of real works,a finite elementmodel(FEM)for the three⁃dimensional new bucket foundation breakwater has been established,and the stability of the buckethas also been analyzed.It is found from analyses that the calculation between the dynamic displacement and the static displacement is inconsistent.In regard to this problem,an equivalent quasi⁃static method has been proposed,which is amethod transforming the dynamic problems to the static one.Under the action of the dynamic load,the water pressure will rise and reach a stable value;in another situation,the water pressure will also rise under the action of the static force.If the water pressure is equal for the two situations,then the equivalent staticmethod can be applied to the calculation of the dynamic displacement.The key pointof thismethod is to find the relationship between the bottom pore pressure response of the front end of the bucket and the static load,and the relationship between the bottom pore pressure response of the frontend of the bucketand the dynamic load.Based on the two relationships,the relationship between the static load and the dynamic load can be established.From comparison between the numerical simulation results and test results,it is proved that thismethod is reasonable.On the basis of simulating and analyzing the prototype bucket foundation structure,the relationship is approximatively linear between the bottom pore pressure response of the front end of the bucket and the static load under differentmodel sizes and different heights of the load application points.
new bucket foundation breakwater;stability;static load;dynamic load;an equivalent quasi⁃static method
U656.2
A
1009-640X(2015)05-0096-07
10.16198/j.cnki.1009-640X.2015.05.013
2014-12-22
杨立功(1982—),男,河南信阳人,博士研究生,主要从事结构与土的相互作用研究。E⁃mail:65481875@qq.com

