变化水位下温度荷载对大坝工作性态的影响
程中凯,陈勋辉,黄耀英,高 俊
(1.温州市水利局,浙江 温州 325000;2.三峡大学 水利与环境学院,湖北 宜昌 443002)
变化水位下温度荷载对大坝工作性态的影响
程中凯1,陈勋辉2,黄耀英2,高 俊2
(1.温州市水利局,浙江 温州 325000;2.三峡大学 水利与环境学院,湖北 宜昌 443002)
现有拱坝设计规范的温度荷载假定上游库水位固定在正常蓄水位,而实际上游库水位在运行中是不断变化的。研究表明,固定水位与变化水位条件下的温度荷载存在较大的差异。以西南某拱坝为例,对同一高程处温度年变化采用傅立叶级数展开,开展变化水位下拱坝温度荷载的研究,对比分析了固定水位和变化水位下两种温度荷载及温度荷载作用下应力与变形的差异。结果表明:变化水位下温度荷载同固定水位下温度荷载的差值随深度的增加基本呈先增大后减小的趋势。在其他荷载一定时,固定水位温度荷载作用下的变形值稍大于变化水位温度荷载作用下的变形值,最大应力均要大于变化水位温度荷载作用下的最大应力。
固定水位;变化水位;温度荷载;应力;变形
程中凯,陈勋辉,黄耀英,等.变化水位下温度荷载对大坝工作性态的影响[J].水利水运工程学报,2015(5):75-81.(CHENG Zhong⁃kai,CHEN Xun⁃hui,HUANG Yao⁃ying,et al.Impacts of temperature loads on working behavior of arch dam during changing water level[J].Hydro⁃Science and Engineering,2015(5):75-81.)
温度荷载是作用于拱坝的主要荷载之一,对拱坝应力,特别是拉应力影响较大。我国现行设计规范[1-2]中计算温度荷载时假定上游库水位固定在正常蓄水位,且多年平均气温和同一高程的库水温随时间按单一正(余)弦函数变化。然而水库实际运行时上游水位不断变化,固定水位与变化水位条件下的温度荷载存在较大差异,主要表现在:①由于水温与气温的巨大差别,使得拱坝在上、下游面之间存在温差;②温度荷载与水深有关,且库水温度会随水深而变化。因此,水位的变化会对温度荷载产生较大影响,大多数情况下多年平均气温和同一高程库水温随时间变化并不能简单地采用单一正(余)弦函数表示。许多学者[3-10]对高拱坝温度荷载的几种计算方法进行了比较。朱伯芳[11]院士提出了考虑水位变动后温度荷载的改进算法。本文结合西南某拱坝,分别计算固定水位下和水位变化条件下的的温度荷载,讨论两种温度荷载的差异,进而建立三维有限元模型,采用有限元法方法分析不同温度荷载对拱坝应力和变形的影响。
1 考虑库水位变化的拱坝温度荷载计算方法
在变化水位的情况下,某一高程处的坝面温度,在水位以上时采用气温,在水位以下时则采用水温。某一高程处的坝面温度随时间的变化规律可以采用傅立叶级数表示,将水位变化对温度的影响计入到温度荷载的计算中。假定上游坝面温度以一年为周期作周期性变化,则可将上游坝面温度值随时间的变化规律采用傅立叶级数表示如下:

由于正弦和余弦函数的正交性,系数Bn和Cn可按下式计算:

取Δτ=30 d,则p=12Δτ,可得:

经三角变换,(1)式可简化如下:

式中:T(τ)为上游坝面温度;Tum为上游坝面年平均温度;Ti为i月月平均气温;τ为时间(月);τ0为气温年周期变化过程的初始相位;Aun为上游坝面温度按傅立叶级数展开的系数,其符号同Bn。
固定水位下的温度荷载是以上变化水位下温度荷载的一种退化特例,即将以上计算中的上游水位取固定值,且水温和气温年变化直接采用单一正(余)弦函数进行表示计算得到的温度荷载便为固定水位下的温度荷载。本文拱坝温度荷载的计算参照朱伯芳院士在文献[4]中所述方法,并将以上水位变化引起的坝面温度变化参考在内。
2 实例分析
以西南某高拱坝为例,该拱坝坝顶高程610.0m,建基面最低高程为324.5m,最大坝高285.5m,水库正常蓄水位600 m,死水位540 m。坝区无断层分布,层间、层内错动带和节理裂隙是坝区的主要结构面。
2.1 三维有限元模型
(1)有限元模型。依据坝体体型及坝基地质资料,建立三维有限元模型。有限元模型的地基截取范围沿上下游、左右岸以及基岩深度方向各截取2倍坝高的范围,采用六面体八节点等参单元进行网格剖分,坝体单元数为3 940,节点数为5 210,有限元整体模型单元数为10 170,节点数为20 278,坐标系为:x向为横河向,y向为顺河向,z向为垂直向,见图1。
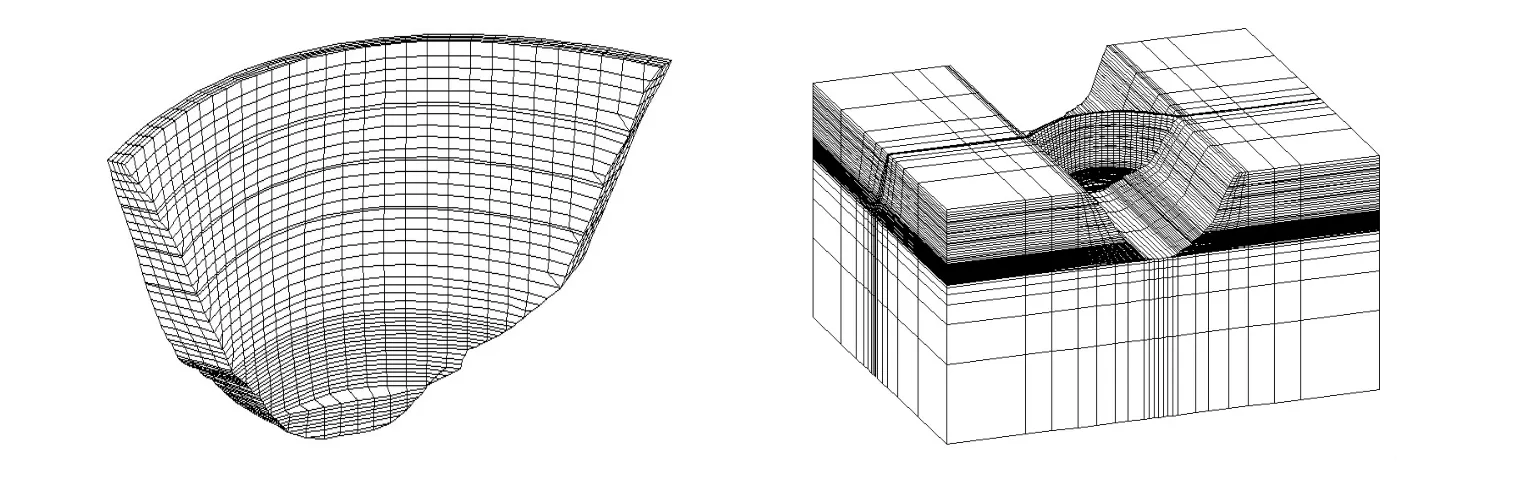
图1 坝体有限元模型Fig.1 A finite elementmodel for a dam
(2)材料参数。假设混凝土坝体和基岩均为各向同性材料,其中坝体混凝土的弹性模量和基岩的变形模量采用相关文献[12]反演计算得到的参数值,其余均采用设计值。坝体及基岩的物理力学参数见表1。

表1 有限元模型中材料参数Tab.1 Material parameters of a finite elementmodel
(3)边界条件。计算域上下游施加顺河向连杆约束,左右岸施加横河向连杆约束,底部施加完全位移约束。
2.2 温度荷载分析
参照文献[5]中的一维数值解法和工程类比法,计算得出3种水库水温分布方案:①方案1,以多年平均气温和水温资料为依据的水温分布;②方案2,增加考虑融雪补给的低温入库水体的水温分布;③方案3,考虑异重流的类比二滩水电站库水温度分布的水温分布。
选取西南某拱坝15#典型坝段(拱冠梁坝段),对比分析固定水位和变化水位下的温度荷载间的差异性见图2~3。

图2 上游面水位过程线及上游坝面典型高程EL580m处水位和温度年变化过程线Fig.2 Hydrograph of water level and hydrograph of temperature annual changes at typical elevation of 580 m at upstream surface of dam

图3 固定水位和变化水位下温度荷载对比Fig.3 Comparison of temperature loads between normal water level and changing water level
分析图2和3可知:
(1)在上游水位变动区域(EL540 m~EL600 m)及其附近(EL518 m~EL540 m)范围内:
①水位变动区,变化水位时上游坝面温度同固定水位时温度差比较大,如在本次计算中上游面高程EL580 m处两者温度最大差值可达11.5℃。
②变化水位下温度荷载同固定水位下温度荷载的差值随深度的增加基本呈先增后减趋势。变化水位温度荷载中的平均温度Tm大于固定水位下温度荷载;等效线性温差小于固定水位下温度荷载。温度荷载最大差值在高程EL518m~EL536m范围附近,温升荷载时,平均温度Tm最大差值为3.48℃,等效线性温差Td最大差距为8.36℃;温降荷载时,平均温度Tm最大差值为2.91℃,等效线性温差Td最大差距为4.74℃。
③在水位变动区附近某一高程,按实际水位变化情况计算得到的温度荷载同采用固定水位条件计算的温度荷载差异较大,平均温度Tm最大差异值约为固定水位下的1.5倍,等效线性温差Td最大差异值约为变化水位下的4.5倍,此对应关系跟朱伯芳院士对此问题的分析结果基本相同[4]。
(2)在高程EL518 m以下:
①变化水位下3种水温分布方案的温度荷载,平均温度Tm由大到小依次对应:方案3>方案1>方案2;等效线性温差大小关系与之相反。平均温度Tm最大差值为3.05℃,等效线性温差Td最大差值为6.06℃。
②由于没有考虑下游水垫塘充水影响,且变化水位下水温分布方案1和方案2以及固定水位下,上游水温此高程以下库水温基本恒定,三者温度荷载基本保持稳定,且平均温度Tm由大到小依次对应:方案1>方案2>固定水位;等效线性温差大小关系与之相反。而固定水位下温度荷载同变化水位水温方案二对应温度荷载接近,是由于固定水位温度荷载计算时,取库底水温12℃,与变化水位下水温分布方案2较接近,可见,固定水位下温度荷载的合理性依赖于经验选取的库底水温的合理性。
2.3 应力变形分析
基于以上温度荷载的分析,变化水位下的温度荷载在水位变动区附近与固定水位下温度荷载的差异很大,且考虑异重流影响水位的变化水温,探讨两者对拱坝应力变形的影响。简化认为坝体及基岩均不透水,计算中也不计入库盘岩体所受水压力,故荷载只考虑坝体自重、作用在坝体的水压力和相应温度荷载,将这些荷载进行组合,得到如下8种工况:工况11,正常蓄水位(EL600 m,下同)+坝体自重+固定水位温升荷载;工况12,正常蓄水位+坝体自重+固定水位温降荷载;工况21,正常蓄水位+坝体自重+水温方案1温升荷载;工况22,正常蓄水位+坝体自重+水温方案1温降荷载;工况31,正常蓄水位+坝体自重+水温方案2温升荷载;工况32,正常蓄水位+坝体自重+水温方案2温降荷载;工况41,正常蓄水位+坝体自重+水温方案3温升荷载;工况42,正常蓄水位+坝体自重+水温方案3温降荷载。
2.3.1 变形分析 通过有限元计算即可得出各工况下拱坝各向位移云图分布,位移的正方向规定为:顺河向(Y轴方向)位移指向上游为正;横河向(X轴方向)位移指向左岸为正,垂直向(Z轴方向)位移竖直向上为正。图4为西南某拱坝在典型工况下坝体总位移下游面分布云图。

图4 坝体总位移下游面分布云图(单位:m)Fig.4 Contours of total displacement of downstream surface of dam(unit:m)
分析图4可知:①以拱冠梁15#坝段为界,顺河向位移同总位移云图分布非常相似,基本呈对称分布,且数值较接近,可以初步推断,坝体总的位移主要沿河流方向向下。②通过计算可知,在其他荷载一定时,固定水位温度荷载作用下的拱坝变形稍大于变化水位温度荷载作用下的拱坝变形,各方向变形的最大差值仅为3.2 mm,约为相应变形值的7%。③变化水位温度荷载中,温度荷载作用下各方案拱坝变形值大小顺序依次为:方案2>方案3>方案1。
2.3.2 应力分析 取典型工况11和工况41下拱坝拱冠梁剖面主应力分布云图(见图5),不同温度荷载作用下拱坝的应力特征值见表2。

图5 拱冠梁剖面第一主应力和第三主应力分布云图(单位:Pa)Fig.5 Distribution cloud picture of first and third main stresses of crown cantilever section(unit:Pa)

表2 不同温度荷载作用下的应力特征值Tab.2 Characteristic values of stress under action of different temperature loads Pa
由图5及表2可知:①各工况下应力分布及应力最大值发生部位基本相同,上游坝面拱端拉应力较大的区域主要集中在高程EL341 m~EL368 m处,各工况下最大值为2.50 MPa;由两岸向拱冠变为压应力,压应力较小,各工况下压应力最大值发生在拱冠的EL350 m附近,为2.55 MPa。下游面压应力较大区集中在左右岸拱端附近高程EL327.5 m~EL395 m处,各工况下最大值达18.7 MPa;下游面基本不产生拉应力。②水压荷载和自重一定时,固定水位下温度荷载作用下的最大应力均大于变化水位温度荷载作用下的最大应力。③变化水位下温度荷载中,方案3对应的温度荷载作用下西南某拱坝的应力最小,主要是因为方案3考虑了异重流的存在,库底水温较高,温度荷载中等效线性温差小于其他工况下温度荷载。
3 结 语
(1)变化水位下温度荷载同固定水位下温度荷载的差值随深度的增加呈先增后减趋势。
(2)其他荷载一定时,基于规范计算得到的固定水位温度荷载作用下的变形值稍大于变化水位温度荷载作用下的变形值,各方向位移最大差值仅为3.2 mm,约为相应变形值的7%。
(3)其他荷载一定时,固定水位下温度荷载作用下的最大应力均大于变化水位温度荷载作用下的最大应力,其中拉应力最大差值为0.5 MPa,约为相应应力值的20%;压应力最大差值为0.9 MPa,约为相应应力值的5%。即采用规范方法计算得到的固定水位下的温度荷载进行拱坝计算稍偏于严格。
[1]SL 282—2003混凝土拱坝设计规范[S]. (SL 282—2003 Design specification for concrete arch dams[S].(in Chinese))
[2]SD 145—1985混凝土拱坝设计规范[S].(SD 145—1985 Design specification for concrete arch dams[S].(in Chinese))cussion on the computation method of temperature load on high arch dams[J].Journal of Hydroelectric Engineering,2010,29(5):35⁃38.(in Chinese))
[3]朱伯芳.论拱坝的温度荷载[J].水力发电,1984(2):23⁃29.(ZHU Bo⁃fang.Researches of arch dam temperature load[J]. Water Power,1984(2):23⁃29.(in Chinese))
[4]朱伯芳,张超然.高拱坝结构安全关键技术研究[M].北京:水利水电出版社,2010.(ZHU Bo⁃fang,ZHANG Chao⁃ran. Researches on the structural safety of high concrete arch dams[M].Beijing:China Water Power Press,2010.(in Chinese))
[5]张国新,杨波,张景华.RCC拱坝的封拱温度与温度荷载研究[J].水利学报,2011(7):812⁃818.(ZHANG Guo⁃xin,YANG Bo,ZHANG Jing⁃hua.Grouting temperature and thermal load of RCC arch dam[J].Journal of Hydraulic Engineering,2011(7):812⁃818.(in Chinese))
[6]麦家煊.拱坝温度场和温度荷载的计算[J].水利学报,1982(1):30⁃45.(MAI Jia⁃xuan.The calculation of arch dam temperature field and temperature load[J].Journal of Hydraulic Engineering,1982(1):30⁃45.(in Chinese))
[7]兰仁烈.拱坝温度荷载计算方法探讨[J].四川水力发电,1991(2):48⁃53.(LAN Ren⁃lie.Discussion on the method for computing temperature loads on the arch dam[J].Sichuan Water Power,1991(2):48⁃53.(in Chinese))
[8]黎展眉.拱坝的温度荷载与温度应力[J].水利水运工程学报,2001(2):31⁃36.(LIZhan⁃mei.Temperature load and stress of arch dams[J].Hydro⁃Science and Engineering,2001(2):31⁃36.(in Chinese))
[9]张国新,陈培培,周秋景.特高拱坝真实温度荷载及对大坝工作性态的影响[J].水利学报,2014(2):127⁃134.(ZHANG Guo⁃xin,CHEN Pei⁃pei,ZHOU Qiu⁃jing.Real temperature load and the influence on the working performance of super⁃high arch dam[J].Journal of Hydraulic Engineering,2014(2):127⁃134.(in Chinese))
[10]李同春,王志强,赵兰浩.高拱坝温度荷载计算方法探讨[J].水力发电学报,2010,29(5):35⁃38.(LI Tong⁃chun,WANG Zhi⁃qiang,ZHAO Lan⁃hao.Discussion on the computationmethod of temperature load on high arch dams[J].Journal of Hydroelectric Engineering,2010,29(5):35⁃38.(in Chinese))
[11]朱伯芳.拱坝温度荷载计算方法的改进[J].水利水电技术,2006,37(12):19⁃22.(ZHU Bo⁃fang.Improvement of the method for computing temperature loads on the arch dam[J].Water Resource and Hydropower Engineering,2006,37(12):19⁃22.(in Chinese))
[12]程中凯.基于蓄水期变形监测资料的溪洛渡高拱坝材料参数反演及变水位下温度荷载分析[D].宜昌:三峡大学,2014.(CHENG Zhong⁃kai.Xiluodu high arch dam material parameter inversion based on the deformation monitoring data during impoundment and analysis of the variation water level temperature loads[D].Yichang:The Three Gorges University,2014.(in Chinese))
Im pacts of tem perature loads on working behavior of arch dam during changing water level
CHENG Zhong⁃kai1,CHEN Xun⁃hui2,HUANG Yao⁃ying2,GAO Jun2
(1.Water Conservancy Bureau ofWenzhou,Wenzhou 325000,China;2.College of Hydraulic&Environmental Engineering,China Three Gorges University,Yichang 443002,China)
The present design specifications for the arch dam assume that the water level in the reservoir is normal at the normalwater level for computing temperature loads,however,thewater level varies continuously in fact.The research results show that there exists a large difference of the temperature loads between the normalwater level and changing water level.This paper takes an arch dam located at the southeast of China as an example.According to the temperature changes at the same elevation,the annual temperature change is expanded by Fourier series,the temperature loads at different water levels are analyzed,and some comparisons are made for the stresses and deformations under temperature loads at the normal water level and the changing water level.The analysis results show when the depth ofwater increases,the difference values of the temperature loads at the normalwater level and the changing water level increase first and then decrease.While other loads keep constant,the stresses and deformations under the temperature loads at the normal water level are greater than those at the changing water level.
normal water level;changing water level;temperature loads;finite element;stress;deformation
TU37
A
1009-640X(2015)05-0075-07
10.16198/j.cnki.1009-640X.2015.05.010
2015-01-26
国家自然科学基金资助项目(51209124)
程中凯(1989—),男,山东日照人,助理工程师,硕士,主要从事水工结构工程安全监控研究。E⁃mail:chengzhongkai007@126.com

