一种模型模拟结果的统计检验方法

周继华, 来利明, 郑元润,*

1 中国科学院植物研究所, 北京 100093 2 中国科学院大学, 北京 100049

一种模型模拟结果的统计检验方法

周继华1,2, 来利明1, 郑元润1,*

1 中国科学院植物研究所, 北京 100093 2 中国科学院大学, 北京 100049

模拟结果的准确性是衡量生态学模型是否成功的关键，但采用统计学方法判别模型模拟结果与观察值相符程度的报道较少。根据两个直线回归方程能否合并为一个方程的统计学检验方法，提出了通过检验观察值与模拟值直线回归方程和1∶1直线方程截距与斜率是否相同，进而在统计显著水平上判断生态学模型模拟值与观察值一致性的统计学检验方法。数据检验表明，此方法可以较好解决判断生态学模型模拟结果准确性的问题。

生态学模型; 模拟精度; 统计学检验

采用数学模型模拟自然及社会中发生的各种过程是学科发展成熟的重要标志，只有对这些过程有较为清晰的认识时才能采用模型进行模拟。随着研究的不断深入，在包括生态学在内的自然与社会科学中开展了大量经典的模型研究工作[1-2]。但关于模型模拟结果与观察值相符程度的检验，也即模型的验证一直是一个非常薄弱的环节[3]。模型能否在统计显著水平上准确模拟所研究的自然现象一直是一个难题[4-5]。目前的生态学文献中对模拟值与观察值相符程度进行统计检验的研究较少。一般的方法是作出模拟值与观察值的散点图显示模拟结果的优劣，并对观察值与模拟值进行回归分析[1, 3-4]；有些通过分析模拟值在1∶1直线两侧的分布情况，判断模型模拟结果的准确性[3, 6]，再进一步则是比较观察值与模拟值差值绝对值的大小，绝对值越小，模拟值与观察值相符越好，模型的模拟结果越好[6]。近年来一些研究采用均方根误差、绝对误差等统计量判断模型模拟结果的优劣[7]。但上述方法的共同缺点是不能从统计学上解释模拟值与观察值的相符程度，也即不能在统计意义上说明模型模拟结果的准确性，这无疑会增加使用模型进行预测与管理的不确定性，甚至会导致产生错误的结论。因此，在统计意义上判别模拟结果是否与观察值相符是一个亟待解决的问题。本文基于统计学检验两种回归直线是否来自同一总体，能否合并的原理提出了检验模型模拟结果与观察值是否在统计学上一致的方法，为生态学乃至所有模型的检验提供了一种简单易行的方法。

1 方法

统计学上，可以检验两种直线是否来自同一总体，即，通过检验直线回归方程(1)、(2)之间的斜率b1,b2和截距a1,a2是否存在显著差异，判断它们是否来自一个总体[8]。

(1)

(2)

检验回归系数b1和b2有无显著性差异的方法为[8]：

假设，H0：β1-β2= 0

备择假设，β1-β2≠ 0

检验统计量：

式中,b1,b2分别为两条回归直线的截距，n1，n2分别为用于建立直线回归方程(1)和(2)的观察数据的样本含量。SX1X1与SX2X2分别为回归直线方程(1)、(2)中X的校正平方和，以直线回归方程(1)为例，X的校正平方和SXX可以表示为：

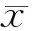
式中，MSe1与MSe2分别为回归直线方程(1)、(2)的剩余均方，以直线回归方程(1)为例，MSe1可以表示为：

式中，SX1Y1为直线回归方程(1)中观察值XY的校正交叉乘积和，可以表示为：

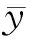
SY1Y1为回归直线方程(1)中关于Y的总校正平方和，可以表示为：

通过上述计算，可以求得tb，以n1-2+n2-2为自由度查t的双侧分布表，如果计算所得tb值小于查得t值，则接受零假设，认为b1=b2，否则认为b1与b2不同。

检验回归系数a1和a2有无显著性差异的方法为[8]：

假设，H0：α1-α2= 0

备择假设，α1-α2≠ 0

通过上述计算，可以求得ta，以n1-2+n2-2为自由度查t的双侧分布表，如果计算所得tb值小于查得t值，则接受零假设，认为a1=a2，否则认为a1与a2不同。

为说明此方法的具体使用过程，以虚拟的植被净第一性生产力观察值与模拟值为例说明此方法的具体计算过程，分别采用两个模型的模拟值与观察值进行分析(表1)。尽管表1与图1有些重复，但为了便于理解此方法，二者均保留在文中。

2 结果

查t分布表得t10, 0.05(双侧)=2.228。对于回归直线2，t值均大于2.228，模型2的模拟值在统计意义上与观察值显著不同，而对于回归直线1，t值均小于2.228，模型1的模拟值在统计意义上与观察值不存在显著区别(表2)。也即模型1可以准确模拟观察值，而模型2模拟效果较差。

表 1 植被净第一性生产力观察值与模拟值(t hm-2 a-1)

表2 模拟值与观察值回归直线与1∶1 直线的统计学参数

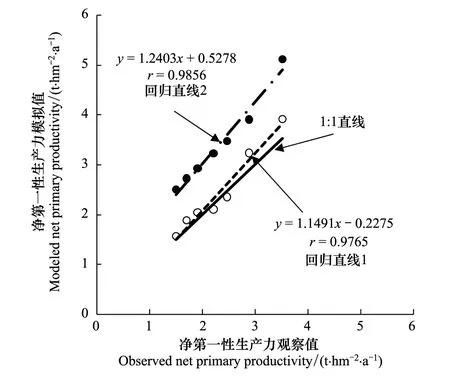
图1 回归直线与1∶1直线的关系Fig.1 Relation between 1∶1 line and regression lines

3 讨论

在一些生态学模型中，仅比较模拟值与观察值随时间的变化，通过变化趋势是否一致，确定模型模拟结果的准确性，有时在某一时间点，观察值与模拟值差别较大[1, 3]。有的模型比较不同模型模拟值在观察值1∶1直线两侧的分布，但当多个模型的模拟值分布趋势一致时，难以判断模型的模拟能力[4]。有的模型比较观察值与模拟值回归直线和观察值1∶1直线的接近程度，但仍属于定性比较[6]。比较不同模型模拟结果的均方根误差、绝对误差也可定量比较不同模型的模拟能力[7]。由于本文主要为方法介绍，采用的两组虚拟模拟数据差别较大，因而，通过上述方法也可以判断模型1的模拟效果要好于模型2，但不能说明模拟值与观察值的相符程度是否达到统计显著水平，也即模拟结果是否在统计水平上可信。

其次，由图1可见，回归直线1与2的相关系数均达到统计显著水平，有时错误地认为两个模型的模拟值均与观察值相符较好，但采用上述方法[6]也可发现回归直线2偏离了1∶1直线，而回归直线1与1∶1直线较为接近。通过本文提出的检验方法可以简单而有效地检验模型对观察值的模拟是否达到了统计显著水平，能够更加客观地评估模型的优劣，建议在生态学模型验证时采用这一方法。但由于生态过程太过复杂，目前的研究深度仍很有限，许多生态学模型的模拟结果仍与观察值有较大差异，采用本文的方法评估模型模拟结果的准确性可能会得出许多模型不能真实模拟自然过程的结果，有待于对生态过程更为深入的理解，进而开发模拟能力更强的模型。

[1] Burns T P, Rose K A, Brenkert K A. Quantifying direct and indirect effects of perturbations using model ecosystems. Ecological Modelling, 2014 (published on line). DOI: 10.1016/j.ecolmodel.2013.12.017.

[2] Black K, Davis P, Lynch P, Jones M, McGettigan M, Osborne B. Long-term trends in solar irradiance in Ireland and their potential effects on gross primary productivity. Agricultural and Forest Meteorology, 2006, 141(2/4): 118-132.

[3] Bullied W J, Flerchinger G N, Bullock P R, Van Acker R C. Process-based modeling of temperature and water profiles in the seedling recruitment zone: Part I. Model validation. Agricultural and Forest Meteorology, 2014, 188: 89-103.

[4] Tayfur G, Zucco G, Brocca L, Moramarco T. Coupling soil moisture and precipitation observations for predicting hourly runoff at small catchment scale. Journal of Hydrology, 2014, 510: 363-371.

[5] Snell R S, Huth A, Nabel J E M S, Bocedi G, Travis J M J, Gravel D, Bugmann H, Gutiérrez A G, Hickler T, Higgins S I, Reineking B, Scherstjanoi M, Zurbriggen N, Lischke H. Using dynamic vegetation models to simulate plant range shifts. Ecography, 2014, 37: 1-14.

[6] Qiu G Y, Yano T, Momii K. An improved methodology to measure evaporation from bare soil based on comparison of surface temperature with a dry soil surface. Journal of Hydrology, 1998, 210: 93-105.

[7] Zhu L H, Zhao X C, Lai L M, Wang J J, Jiang L H, Ding J Z, Liu N X, Yu Y J, Li J S, Xiao N W, Zheng Y R, Rimmington G M. Soil TPH concentration estimation using vegetation indices in an oil polluted area of eastern China. PLoS ONE, 2013, 8(1): e54028.

[8] 杜荣骞. 生物统计学. 北京: 高等教育出版社, 海德堡: 施普林格出版社, 1999.

A statistical method for validation of ecological models

ZHOU Jihua1,2, LAI Liming1, ZHENG Yuanrun1,*

1InstituteofBotany,ChineseAcademyofSciences,Beijing100093,China2UniversityofChineseAcademyofSciences,Beijing100049,China

Statistical validation has rarely been conducted to examine the consistency between observed data and the output of ecological models, although such validation is critical for determining the goodness-of-fit of such models. Based on the statistical principle of whether two regression models can be combined, a statistical method is proposed for validating ecological models. In the method, a linear regression is fit to observed (x-axis) and modeled (y-axis) data, then tested for significant differences in slope and intercept from the liney=x. A case study shows that the method could be used to validate ecological models.

ecological model; model validation; statistical test

国家自然科学基金项目(91225302)

2014-02-26; < class="emphasis_bold">网络出版日期:

日期:2014-12-04

10.5846/stxb201402260333

*通讯作者Corresponding author.E-mail: zhengyr@ibcas.ac.cn

周继华, 来利明, 郑元润.一种模型模拟结果的统计检验方法.生态学报,2015,35(19):6435-6438.

Zhou J H, Lai L M, Zheng Y R.A statistical method for validation of ecological models.Acta Ecologica Sinica,2015,35(19):6435-6438.