城市生态网络功能性连接辨识方法

陈春娣, Meurk D. Colin, Ignatieva E. Maria, Stewart H. Glenn, 吴胜军

1 中国科学院水库水环境重点实验室, 中国科学院重庆绿色智能技术研究院, 重庆 400714 2 新西兰皇家科学院土地保护研究所, 新西兰 基督城 7608 3 林肯大学, 新西兰 基督城 7674

城市生态网络功能性连接辨识方法

陈春娣1,3,*, Meurk D. Colin2, Ignatieva E. Maria3, Stewart H. Glenn3, 吴胜军1

1 中国科学院水库水环境重点实验室, 中国科学院重庆绿色智能技术研究院, 重庆 400714 2 新西兰皇家科学院土地保护研究所, 新西兰 基督城 7608 3 林肯大学, 新西兰 基督城 7674

城市生态网络是景观生态学应用领域研究的热点和重点之一，识别、评估生境之间的连接是构建生态网络的关键环节。在总结已有连接辨识方法的基础上，提出采用最小费用模型和图论分析相结合的方法，探讨功能性连接的辨识和优先恢复途径。以新西兰基督城为案例，分别利用景观发展强度指数建立阻力面，新西兰鸡毛松(Dacrycarpusdacrydioides)种子最大传播距离作为连接阈值来模拟、评价网络连接。结果表明：在1200 m距离阈值下，共有408条连接，其重要性分为10类。其中Richmond—Petrie公园，Hansons—Auburn保护地，Centaurus公园—King George保护地是整个生态网络的关键连接；若去除，景观整体连接度将下降31.73%。此外，研究发现连接重要值与两端的源面积之和没有显著相关性，即面积大的源斑块之间的连接不一定对网络构建起关键作用，这一结论还有待进一步证明。针对缺少动物迁移资料的城市环境，改进最小费用模型和网络连接分析的部分参数；可操作性与实用性强，对中国城市区域生态恢复建设、栖息地选择具有借鉴意义。

城市生态网络; 功能性连接; 乡土栖息地; 最小费用模型; 图论; 乡土树种子传播

在城市化、工业化进程不断加快，自然栖息地破碎与部分生境消失不可避免的背景下，通过研究景观连接性，构建生态网络(Ecological Networks)，以少量的生态用地保障城市区域生态安全[1]，缓解土地保护和城市建设发展的用地矛盾，是当前景观生态学应用领域研究的热点和重点之一。景观的连接性是指景观促进或阻碍生物体或某种生态过程在斑块间运动的程度[2]。保护生物学相关文献表明，提高景观连接度可以有效地促进生态系统中的各种生态过程，如动物迁移[3]、种子扩散[4]，基因流动[5]等，从而减小局域种群的灭绝风险，进而维持景观生态过程及格局的完整性和连续性[6]。

景观图论采用拓扑学方法把景观镶嵌体中的斑块、廊道、基质等抽象为节点、连接以及他们之间的生态流关系[6](图1)。该理论与方法已逐步应用于景观生态网络构建中[7]。相比早期的网络研究注重景观结构上的实体连接(Structural connectivity)，图论方法更强调功能性连接(Functional connectivity)(图1)，即某种生态过程能够发生的景观组分间有效联系[8]。例如人工环境基质下，两个绿地斑块没有结构连接，但一块绿地中的乡土树种子能够借助风力飞到另一块落种扎根，或小型哺乳动物能够通过其中转迁徙，这两块生境即为功能性连接。功能性生态网络整合复杂的生态过程分析在景观格局优化上，在生境破碎已成趋势，恢复结构性连接越发困难的情况下，可操作性更强，意义更加显著。

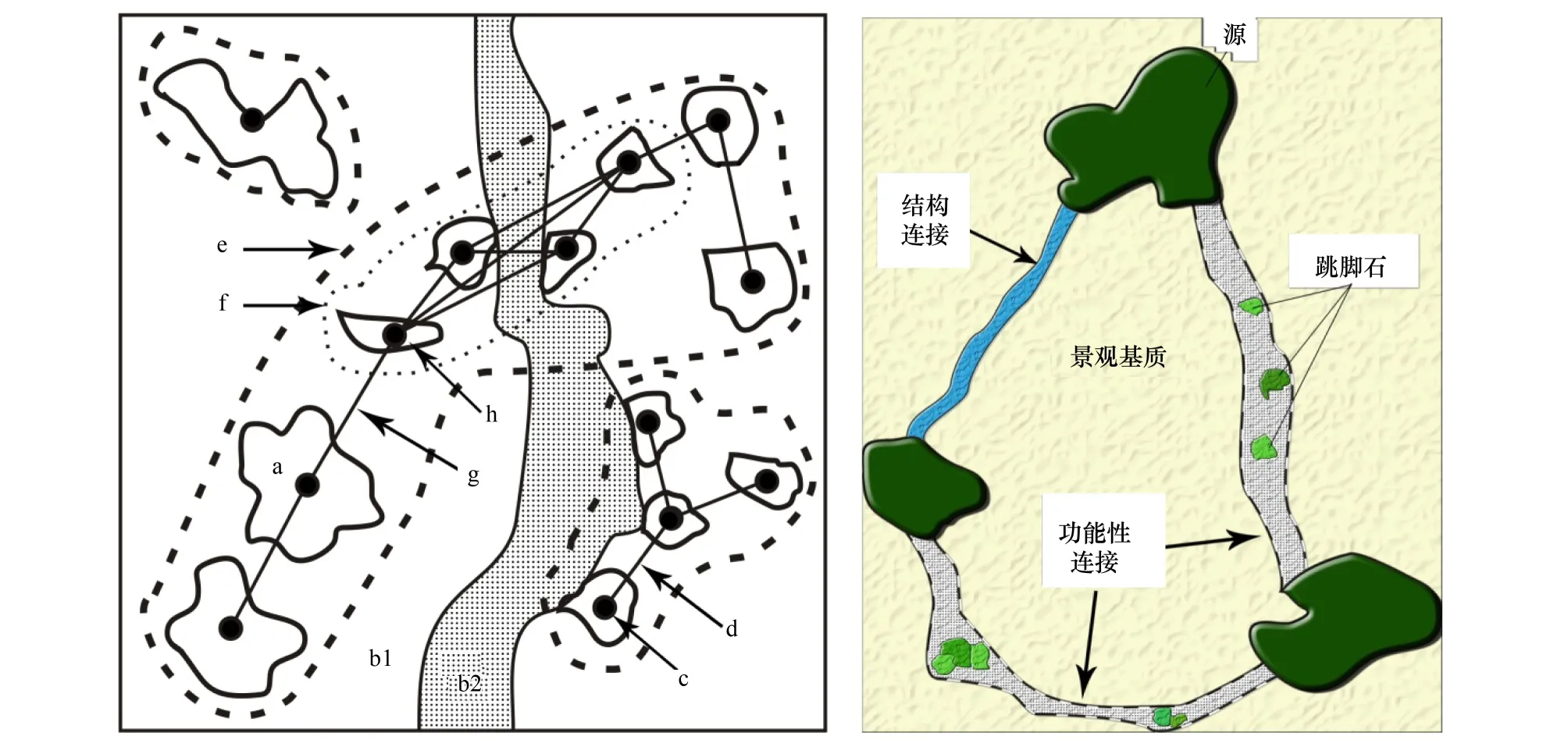
图1 基于图论视角的功能性生态网络Fig.1 Functional connectivity based on landscape graph theorya:源生境斑块；b (b1, b2):景观基质；c: 节点；d: 连接；e: 景观组分，相互连接的斑块构成一个组分；f: 景观亚组分，一个景观组分中，有更多连接的斑块组成亚组分；g: 关键连接，若移除，景观组分的连接性将受到威胁；h: 关键节点，若移除，景观组分的连接性将受到威胁[9]; 其中，d为抽象的功能性连接，常由跳脚石斑块组成，而b2为线型要素，视为结构连接

提取功能性连接常用的方法有两种：(1)直接追踪动物迁移，再根据物种疏散模型或复合动力模型，计算迁移路径的概率值，构建网络结构[10]。模型需要详尽的信息和数据支持，为格局与过程相互关系提供了直观的模拟，但研究难度较大，较耗时[9]，尚不成熟。如Lookingbill等利用J-walk模型模拟10万只松鼠的运动路径来确定生态网络，但模型不能体现种群的记忆能力，其构建的网络生物学意义仍不足[11]。且该类研究多针对野生自然环境，很少应用于城市环境。(2)基于最小费用模型，通过计算物种从源经过不同阻力的景观类型所耗费的费用或克服阻力所作的功模拟最小成本路径，再根据生态过程所对应的距离阈值来辨识连接，以构建网络[12]。该方法在国外已成为以野生动物保护为目标的自然栖息地恢复常用方法，在国内被较多地应用于城市环境，如俞孔坚等构建了北京生态安全格局[13]；Kong等构建了济南城市绿网[14]；Teng等运用于武汉城市绿道规划[15]。

建立阻力面，即评估不同的景观类型对物种迁移的阻碍能力是最小费用模型所需数据[12]。常用的方法是基于土地适宜性评价结合专家经验为土地利用/覆盖类型打分：①根据植被覆盖度或植物群落多样性评价土地适宜性[14]。②选择代理物种，如蝴蝶[16]，刺猬[17]，通过调研文献获取其生活习性，评估土地阻力值。确定生态过程对应的距离阈值也有两种思路：①根据焦点/代理物种的习性，如摄食、筑巢、最大一次迁徙距离来判断。Minor等将北美画眉鸟(Hylocichlamustelin)一次飞行最大距离1500 m作为判断斑块连接的阈值[9]；Pereira等以欧洲龟(Emysorbicularis)最大一次爬行距离2000 m研究池塘水域功能性连接[18]；②尝试不同的阈值，依据统计学原理，寻找突变点或稳定值，如Devi等[19]，García-Feceda等[20]研究不同连接指数对阈值变化的敏感程度，为网络构建提供合理阈值。

相比动物追踪，基于最小费用模型的路径辨识可以实现在缺少观测资料的情况下，较快捷地模拟斑块间联系，是目前应用最广泛的方法。但在阻力面赋值时，主观性很强，如不同专家会对相同的研究区给出不同的阻力值；且偏重于考虑连接本身的属性，如两端斑块的生境面积或质量，忽略了连接在整个网络结构中的重要性以及与其他景观要素的关系。

在总结已有研究的基础上，本研究提出最小费用模型与网络连接性分析相结合的方法辨识、评估功能性连接。以新西兰基督城为案例，本研究基于课题组长期的基础性研究，包括全市绿地/自然栖息地植被调查，乡土植物种子扩散实验，采用基于图论的景观连接度指数、生境质量综合评估和GIS相结合的技术，为“恢复栖息地，布置城市在一张绿色编制的网格中”震后重建设想，提供生态学意义明晰的空间规划途径。其中，采用景观发展强度指数构建阻力面，减少专家评分的主观性；以乡土树种子传播距离作为网络连接的距离阈值，适合于缺少动物迁移观测资料的城市环境，为中国城市生态网络理论和方法研究提供参考。

1 研究区概况

基督城(Christchurch, 43°51′S, 172°65′E)位于新西兰南岛东海岸坎特伯雷平原上(图2)，地势平坦，属于凉爽温带海洋性气候，四季如春，年均气温11.7 ℃；降水丰富，年均650 mm，分布均匀。整个市域面积约1426 km2，市区452 km2，人口约37.9万(2013年6月)，是新西兰南岛第一大城市。市内共有公园792个，约占市区总面积1/3。1997年被联合国授予“Garden City of the World”荣誉。该区顶级森林群落为海岸区常绿针阔混交林带，代表性树种为新西兰鸡毛松(Dacrycarpusdacrydioides)，新西兰罗汉松(Podocarpustotara)，新西兰黑松(Prumnopitystaxifolia)，新西兰甘蓝树(Cordylineaustralis)，新西兰茶树(Kunzeaericoides)等[21]。

古生代时期冈瓦纳古陆(Gondwana)分裂，新西兰独立成孤岛，逐步发育成岛屿生态环境，物种资源丰富且独特，具有很多单一科、属、种，如国家标志性植物银蕨(Cyatheadealbata)，与我国的珍稀植物桫椤同属，均是恐龙时代留下的活化石植物。该国是英联邦国家，自1840年以来，欧洲移民不断涌入。早期城市环境建设以营造欧洲和北美城市景观为指导，大量带入的外来物种，造成生物入侵、本地种濒临灭绝等生态问题。以坎特伯雷平原为例，目前仅存约1%的本土植物，该国可能是世界上在如此短的人类定居时间内，物种消失最快、数量最多的国家[22]。近几十年，政府和民众意识到本土物种的保护对于岛屿生态系统健康稳定，以及营造地域特色景观的重要性。

2 研究方法

本研究范围为基督城市区核心区，面积138.68 km2。采用的数据包括2009年基督城土地利用/覆盖图(来源于新西兰环境保护部)，数据源为Landsat7ETM分辨率为15 m的遥感影像，解译精度93.9%，分类体系采用联合国粮农组织(FAO)的国际分类标准[23]。数据库包括全市范围地形图、水系分布、以及经实地调查绘制的绿地斑块图(包括各类公园和自然保护地，最小斑块面积8 m2)和乡土树种分布图(GPS定位到每棵树龄在10a以上的树)。

2.1 最小费用模型

2.1.1 源确定

模型应用首先需确定源，即生态过程发展的源头[24]。定义源为乡土动植物栖息地，采用植物群落特征属性综合判别，不仅涉及植物多样性，还涉及区系结构、来源结构、优势种结构、群丛结构、树龄等内容，比单一的多样性指标更能反映群落特征，以及所蕴含的复杂生态过程[25]。自2001年，课题组受新西兰环境部委托，调查、评估全市所有绿地/自然生境，建立城市植物、栖息地数据库，每年更新维护，部分成果见文献[26-28]。基于已有数据，以植物多样性指数排名在前50%，群落优势种中乡土树种比例在40%以上，且树龄在15a以上的标准筛选确定源斑块。

2.1.2 景观发展强度构建阻力面

基于土地能值分析的景观发展强度(LDI)指数由Brown等人提出，应用于流域尺度到单个的湿地。以土地利用/覆盖为基础数据，LDI通过计算土地单位面积上不可更新资源的投入与消耗，包括化石燃料、化肥、杀虫剂和水资源[29]，评估人类对土地的开发利用强度。某类型土地LDI值越高，人类影响越大。研究表明LDI与污染物负荷成正比[30]，与生境质量、生物多样性成反比[31]，是一个能够很好指示生态系统功能的指标。根据生物多样性与LDI的显著反比关系，采用LDI值来构建阻力面；利用ArcGIS10空间分析模块和Linkage Mapper Toolist[32]提炼低景观发展强度连接，即适宜物种迁移的低阻力路径。

2.2 网络连接重要性评价

Pascual-Hortal等提出了基于图论理论的网络整体连接度指数(IIC) 等新指标及算法[33]，与之前网络分析常用的连接性指数(如α、β和γ指数)相比，将生境的属性特征(如面积，保有物种丰富度等)整合到算法中，更准确地衡量网络连接性[34]；同时可以分析景观要素(节点和连接)对于网络连接度的贡献值，确定优先保留/恢复[33]。相关的公式及解释如表1。

从景观图论的角度，采用组分数与斑块总数之比评价景观破碎度，公式如下：

F=NC/T

式中，NC为组分数；T为某类型斑块总数；F值越大，表明景观的破碎程度越高。

2.3 连接阈值确定

选定基督城内基质较均一(如草本覆盖)，存在目标树种(10a以上成熟林)的自然保护地作为实验地，每6个月对样地普查，从源生境向外扩展，寻找乡土树幼苗，记录数量与距源距离[35]。初步拟定以新西兰鸡毛松(D.dacrydioides)传播最大距离1200 m作为连接阈值。为了验证1200 m是否对网络格局分析有效，以100 m为间隔选取100 m至20000 m之间的距离，在ArcGIS10和Conefor Inputs插件下分别计算相对应的连接度指数，评价不同距离情境下，各连接度指数变化情况，确定较优的阈值。

采用Conefor2.6软件计算最优距离阈值下的重要值dIIClink，在SPSS21.0软件采用层次聚类分析法(Hierarchical Cluster Analysis)结合决策者实际需求，将重要值划分10个等级，以此判断城市重建中，哪些连接是优先恢复。并进一步分析连接的空间特征，以及与源斑块面积等影响因素之间的相互关系。

表1 基于图论的连接度指数

3 结果与分析

3.1 最小成本路径模拟

依据上述研究方法，从545个绿地/自然栖息地中得到221个作为源斑块，占研究区生境斑块总量的40.6%，面积共6.6 km2，占总生境面积的50%。其中，小于1 hm2的源数量为133，占源总数的60.2%，而面积仅占9.5%，符合城市环境中，斑块破碎化严重，小面积栖息地占绝对数量的特点。基于LDI赋值的景观阻力面，自然保护地等类型赋值1，高密度中央商务区赋值最大10。图3为源间最小成本路径及廊道模拟，共682条，长度在15—20723 m之间。

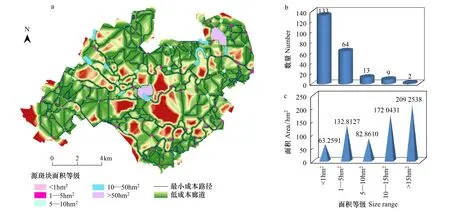
图3 研究区最小成本路径与廊道模拟(a)；不同等级斑块所对应的斑块数量(b)；不同等级斑块的面积总和(c)Fig.3 The east-cost pathways and corridors of Christchurch′s ecological network (a); Graph of source (habitat) size range to patch number (b); Graph of source size range to its total area (c)

3.2 连接指数变化分析与距离阈值的验证

图4显示在不同距离阈值下连接数NL，组分数NC，景观破碎度F和整体连接值IICnum的变化。从100 m到20000 m，NL与距离呈显著正相关(Pearson′sr=0.654,P=0.003)，在5000 m处达到饱和。景观组分数随距离增大而逐步减少，当阈值为100 m时，景观中存在170个组分，占斑块总数量的76.92%，景观破碎度高；当阈值为1500 m时，NC值为7，占总数量3.17%。阈值继续扩大，NC值保持在6，呈饱和态势。通过综合比较，1000—1500 m之间均是较为合理的阈值，因为当距离较小时，研究区景观划分的组分数多，连接少，破碎度大，不能实现网络构建目标；而该值过大时，研究区的景观组分数和破碎度达到饱和，景观连接度过高会导致规划可操作性降低。因此选定的1200 m是网络分析合适的阈值。以此构建的城市生态网络，共408条连接，占研究区最小成本路径总数的60%；景观组分数为14，其中斑块和连接数最多的是北部组分1和南部组分2(图5)，整体景观破碎度为6.33%。

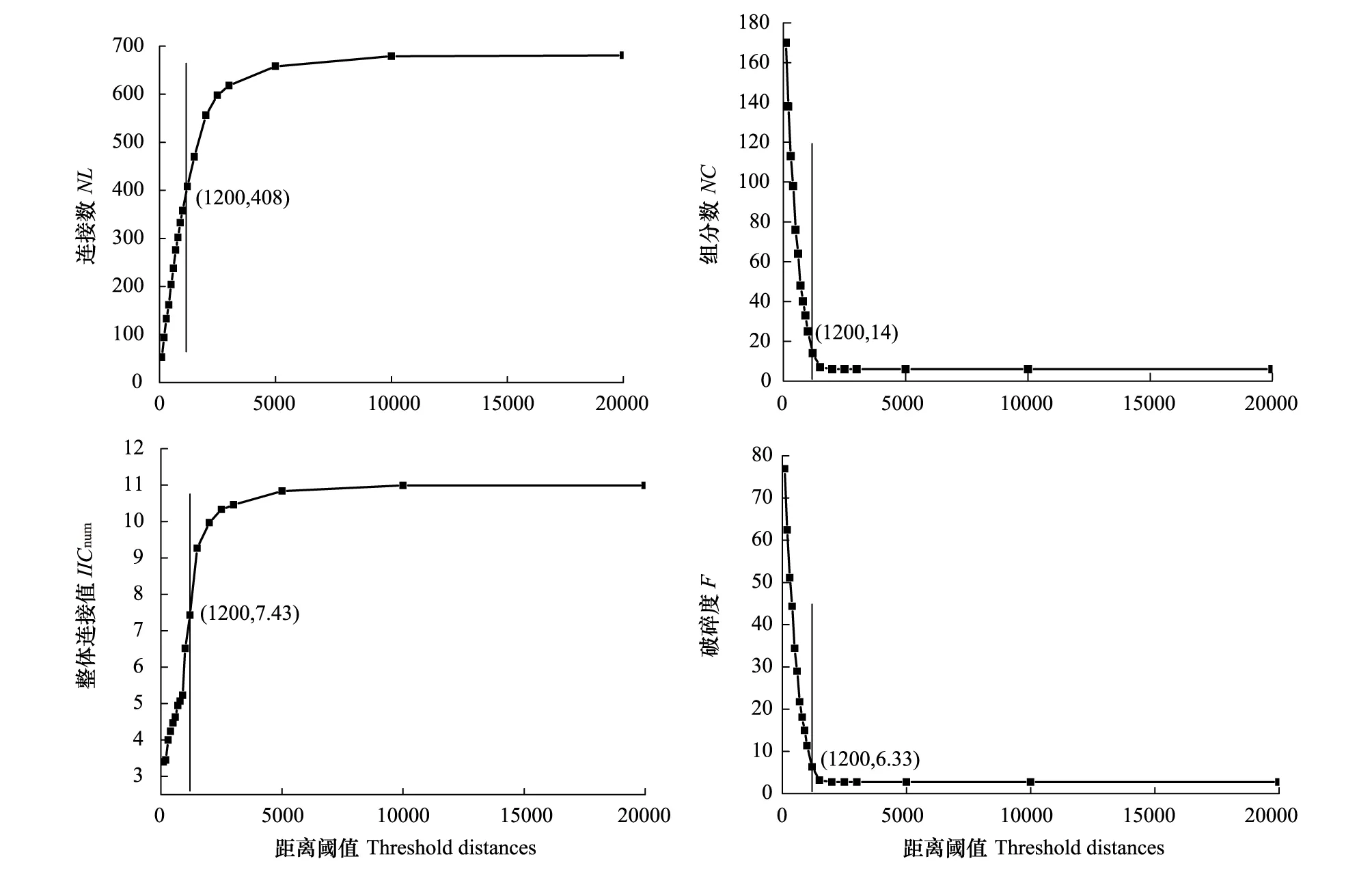
图4 不同距离阈值下网络连接指数值Fig.4 Results of connectivity indices in respond to different threshold distances IICnum取值均除以1012

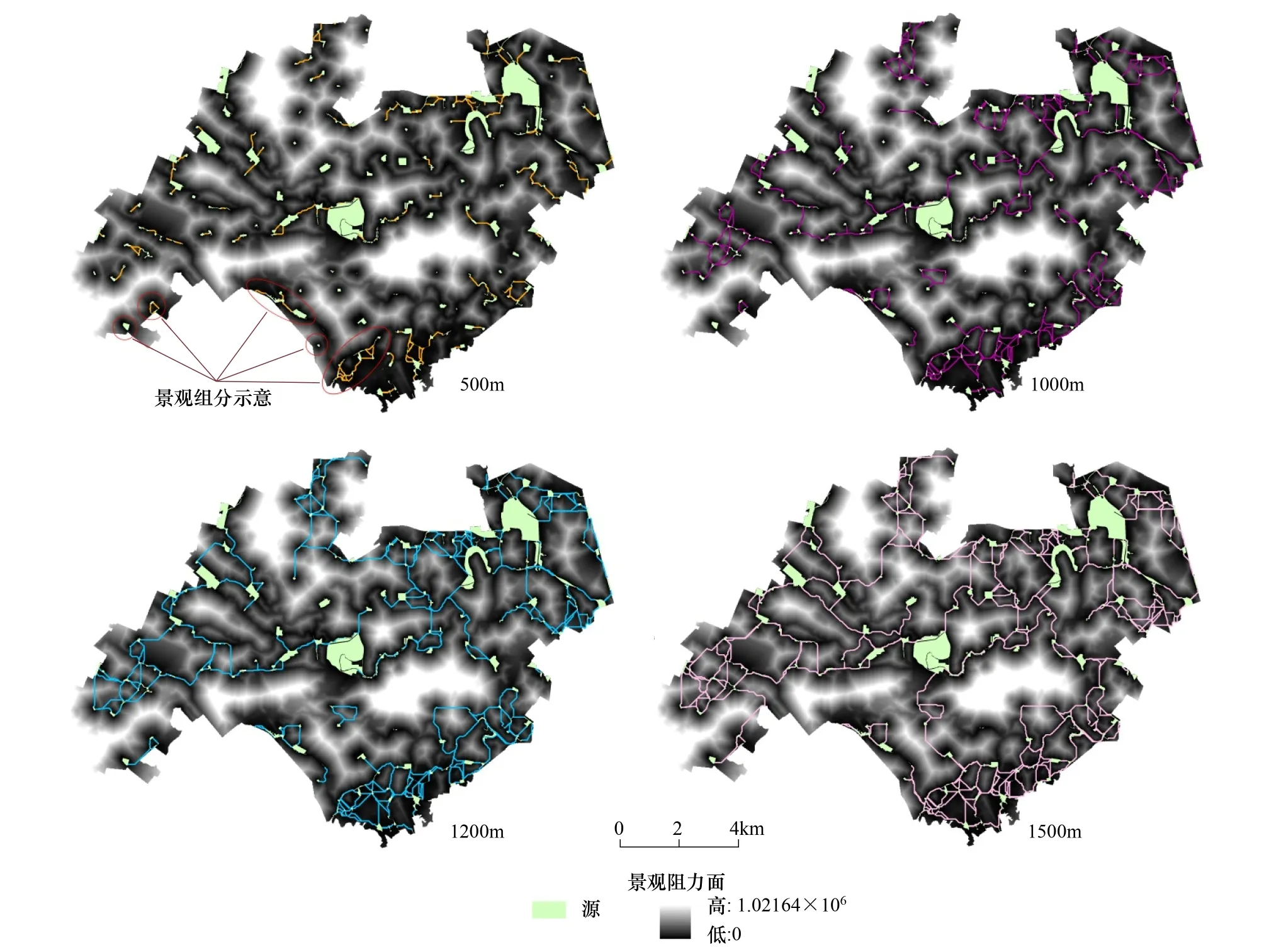
图5 500, 1000, 1200, 1500m距离阈值下功能性连接模拟Fig.5 Functional connectivity simulation under 500, 1000, 1200, 1500m threshold distances

3.3 功能性连接重要性评价

1200 m阈值下共提取408条功能性连接，dIIClink取值范围在1×10-6到17.77之间，最重要的连接是395—367连接，即Richmond儿童公园与Petrie公园之间，若被移除，景观整体连接度将下降17.77%。图6显示该条连接(红线标示)是最复杂的景观组分1内东北部和中西部两大亚组分的唯一连接，如果该条连接中断，景观将会被分割为更多组分，整体破碎度提高；同样，重要性第二的连接位于南部景观组分2中，连接其内部的东西两大亚组分。

进一步对连接重要值dIIClink与两端源斑块面积之和做相关性分析发现，这两者之间不具线性相关(Pearson′sr=0.078，P=0.118)。通常理解，面积越大的源能够保育更多的物种，会更有效促进生态系统物质能量流动；但是，本研究发现面积小的源斑块仍可以对景观的完整性、连通性起到至关重要的作用。

图6表明，重要值大的连接绝大部分是组分间的唯一通道，即关键连接(图1)，对网络结构的完整性起着关键作用。连接的下界面大部分是生境一般的土地利用/覆盖类型，如395—367连接穿过一个社区中心，199—18连接则是学校草坪操场。在栖息地恢复重建时，建议部分开辟为乡土物种栖息地，完善“跳脚石”斑块的生境质量，以加强整体网络连接。

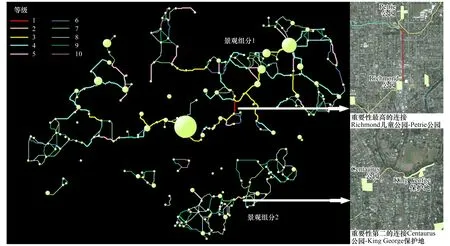
图6 1200m阈值下功能性连接重要性空间评价图Fig.6 Link importance geospatial evaluation map under 1200m threshold distance

4 讨论

目前，很多文献针对源斑块重要性[36-37]或生态网络整体拓扑关系度量[38-40]，而较少关注源之间的连接、其重要性以及如何真正落实到空间规划上。结构性连接目前还存在一定争议，如有学者指出其负面效应包括增加火灾蔓延、疾病/害虫传播、扩散干扰源的风险[41-42]；功能性连接是以某种代表性的生态功能作为代理，假设其需求得到满足，其他物种的需求也可以得到满足[43]。其实体是由散布在最小成本路径上，阻力较小的一般生境斑块组成。不同于源生境，通常因保育丰富的物种，审美质量较高而受到社会普遍关注，能够在城市快速发展中被“政策性”保留下来，而一般生境随时面临开发建设的蚕食。研究这些斑块的重要性，筛选优先保留或恢复的斑块，可以有效地促进生态网络连接，对城市生态保护、土地规划与管理实施具有重要意义。

最小费用模型基于GIS平台，特点在于将空间规划与某些生态过程联系起来，数据需求量少，最终以地图的形式表达，在构建生态网络上具有很大优势，但也存在成本阻力面和连接阈值确定普遍具有主观性的问题。采用由土地能值计算得到的景观发展强度指数(LDI)为土地类型赋值，一定程度减少主观性。然而，值得指出的是，LDI是基于西方国家的土地利用/覆盖类型获得的相对系数，例如均高4层楼的金融区能值最高，LDI值为10，而在中国城市，这类型的土地能值只能在中间水平，建议依据国内土地分类标准，计算与当地社会经济发展状况相符合的LDI值。在重要性等级划分上，大部分研究采用自然断点法[18,39]，而结合聚类分析，根据数值本身的差异来辨识，减少了主观性。

在选择代理物种构建生态网络时，应尽量选择乡土物种，以利于本土生态系统恢复。目前，城市生态网络的构建研究常借鉴森林生态系统中小型哺乳动物的活动特征来确定，属于经验型定义，并未对城市环境做实证研究，忽略了其自然生态系统的特点：面积小、分散布局；高度人工化，外来物种比例大；加之靠近道路、居民区等各种人类活动干扰/威胁源，很难保育有小型哺乳动物。并且，(乡土)动物对栖息地的选择更为苛刻，包括食物、水源、天敌，以及各种干扰，因此，对城市环境动物迁移路径的模拟较困难。相比之下，影响植物种子迁移的因素较单一，已开发的模型较多[44]，易对预测结果进行验证。此外，选择植物更具有代表性。植物是各类物种的载体，是提供生态系统服务的主体，常是一个生态系统健康的直接表征和综合指标，城市生态系统亦不例外。首先存在一个健康的植物群落，才有可能形成生物多样性高的本土生态系统。

本研究基于实验研究，从乡土树种子传播定居的角度确定网络连接，符合城市环境的特点，且规划操作性强，是对基于动物迁移的网络构建研究的创新拓展。作为一种新方法探索，存在一些不足，如景观发展强度指数具有国家区域性，所提出的重要性连接是否对乡土植物群落恢复有显著影响等。因此对于该方法的普适性与合理性还有待更多的案例研究进一步验证。

5 结论

以种子扩散过程作为城市自然栖息地网络构建规则，从连接在整个景观空间结构中的重要性出发，采用最小费用模型与基于图论的景观连接度指数相结合的方法对新西兰基督城进行功能性连接识别。

(1) 以新西兰乡土树鸡毛松(D.dacrydioides)种子最大传播距离1200 m作为连接阈值分析网络，不仅具有生态学意义，而且具有结构意义和较强的规划可操作性。共辨识408条连接，划分为10个等级，其中最重要的连接是Richmond—Petrie公园，Hansons—Auburn保护地，和Centaurus公园—King George保护地，若被移除，整个网络的连接度将下降31.73%。从景观图论的空间特征上显示，这些连接也正是整个景观的关键连接。针对不同等级的连接，结合下界面现状，建议采取不同优先顺序、不同强度的恢复对策。

(2) 连接的重要性与两端源面积之和没有相关关系，不同于通常认为的面积越大的斑块，之间的连接越重要。这一结论还有待进一步研究来证明。但是，建议今后在城市生态网络构建、生物多样性保护空间规划中，除了考虑源斑块属性，还应结合采用的方法，辨识关键连接，加强源之间的物质能量联系。

[1] Brose U. Improving nature conservancy strategies by ecological network theory. Basic and Applied Ecology, 2010, 11(1): 1-5.

[2] Taylor P D, Fahrig L, Henein K, Merriam G. Connectivity is a vital element of landscape structure. Oikos, 1993, 68(3): 571-573.

[3] Uezu A, Metzger J P, Vielliard J M E. Effects of structural and functional connectivity and patch size on the abundance of seven Atlantic Forest bird species. Biological Conservation, 2005, 123(4): 507-519.

[4] Sork V L, Smouse P E. Genetic analysis of landscape connectivity in tree populations. Landscape Ecology, 2006, 21(6): 821-836.

[5] Neel M C. Patch connectivity and genetic diversity conservation in the federally endangered and narrowly endemic plant speciesAstragalusalbens(Fabaceae). Biological Conservation, 2008, 141(4): 938-955.

[6] Urban D, Keitt T. Landscape connectivity: a graph-theoretic perspective. Ecology, 2001, 82(5): 1205-1218.

[7] Dale M R T, Fortin M J. From graphs to spatial graphs. Annual Review of Ecology, Evolution, and Systematics, 2010, 41: 21-38.

[8] Theobald D M. Exploring the functional connectivity of landscapes using landscape networks // Crooks K R, Sanjayan M. Connectivity Conservation. Cambridge: Cambridge University Press, 2006: 416-443.

[9] Minor E S, Urban D L. Graph theory as a proxy for spatially explicit population models in conservation planning. Ecological Applications, 2007, 17(6): 1771-1782.

[10] Gardner R H, Gustafson E J. Simulating dispersal of reintroduced species within heterogeneous landscapes. Ecological Modelling, 2004, 171(4): 339-358.

[11] Lookingbill T R, Gardner R H, Ferrari J R, Keller C E. Combining a dispersal model with network theory to assess habitat connectivity. Ecological Applications, 2010, 20(2): 427-441.

[12] Adriaensen F, Chardon J P, De Blust G, Swinnen E, Villalba S, Gulinck H, Matthysen E. The application of ‘least-cost’ modelling as a functional landscape model. Landscape and Urban Planning, 2003, 64(4): 233-247.

[13] 俞孔坚, 王思思, 李迪华, 李春波. 北京市生态安全格局及城市增长预景. 生态学报, 2009, 29(3): 1189-1204.

[14] Kong F H, Yin H W, Nakagoshi N, Zong Y G. Urban green space network development for biodiversity conservation: Identification based on graph theory and gravity modeling. Landscape and Urban Planning, 2010, 95(1/2): 16-27.

[15] Teng M J, Wu C G, Zhou Z X, Lord E, Zheng Z M. Multipurpose greenway planning for changing cities: a framework integrating priorities and a least-cost path model. Landscape and Urban Planning, 2011, 103(1): 1-14.

[16] Chardon J P, Adriaensen F, Matthysen E. Incorporating landscape elements into a connectivity measure: a case study for the Speckled wood butterfly (ParargeaegeriaL.). Landscape Ecology, 2003, 18(6): 561-573.

[17] Driezen K, Adriaensen F, Rondinini C, Doncaster C P, Matthysen E. Evaluating least-cost model predictions with empirical dispersal data: a case-study using radiotracking data of hedgehogs (Erinaceuseuropaeus). Ecological Modelling, 2007, 209(2/4): 314-322.

[18] Pereira M, Segurado P, Neves N. Using spatial network structure in landscape management and planning: a case study with pond turtles. Landscape and Urban Planning, 2011, 100(1/2): 67-76.

[19] Devi B S S, Murthy M S R, Debnath B, Jha C S. Forest patch connectivity diagnostics and prioritization using graph theory. Ecological Modelling, 2013, 251: 279-287.

[20] García-Feced C, Saura S, Elena-Rosselló R. Improving landscape connectivity in forest districts: a two-stage process for prioritizing agricultural patches for reforestation. Forest Ecology and Management, 2011, 261(1): 154-161.

[21] Meurk C D. Evergreen broadleaved forests of New Zealand and their bioclimatic definition // Box E O, Peet R K, Masuzawa T, Yamada I, Fujiwara K, Maycock P F. Vegetation Science in Forestry. Netherlands: Springer, 1995: 151-197.

[22] Meurk C D. Implication of New Zealand′s unique biogeography for conservation and urban design // Stewart G, Ignatieva M E, Bowring J, Egoz S, Melnichuk I. Globalisation of Landscape Architecture: Issues for Education and Practice. St Petersburg: St Petersburg′s State Polytechnic University Publishing House, 2007: 142-155.

[23] MfE (Ministry for the Environment). New Zealand Land Cover Database 2 User Guide. 2004. http://www.mfe.govt.nz/issues/land/land-cover-dbase/lcdb2-user-guide.pdf

[24] 陈利顶, 傅伯杰, 赵文武. “源”“汇” 景观理论及其生态学意义. 生态学报, 2006, 26(5): 1444-1449.

[25] Pickett S T A, Cadenasso M L, Grove J M, Nilon C H, Pouyat R V, Zipperer W C, Costanza R. Urban ecological systems: linking terrestrial ecological, physical, and socioeconomic components of metropolitan areas. Annual Review of Ecology and Systematics, 2001, 32(1): 127-157.

[26] Stewart G H, Meurk C D, Ignatieva M E, Buckley H L, Magueur A, Case B S, Hudson M, Parker M. Urban biotopes of Aotearoa New Zealand (URBANZ) II: floristics, biodiversity and conservation values of urban residential and public woodlands, Christchurch. Urban Forestry & Urban Greening, 2009, 8(3): 149-162.

[27] Stewart G H, Ignatieva M E, Meurk C D, Earl R D. The re-emergence of indigenous forest in an urban environment, Christchurch, New Zealand. Urban Forestry & Urban Greening, 2004, 2(3): 149-158.

[28] Meurk C D. Recombinant ecology of urban areas // The Routledge Handbook of Urban Ecology. Hoboken: Taylor & Francis, 2010: 198-220.

[29] Brown M T, Vivas M B. Landscape development intensity index. Environmental Monitoring and Assessment, 2005, 101(1/3): 289-309.

[30] Lane C R, Brown M T. Diatoms as indicators of isolated herbaceous wetland condition in Florida, USA. Ecological Indicators, 2007, 7(3): 521-540.

[31] Chen T S, Lin H J. Application of a landscape development intensity index for assessing wetlands in Taiwan. Wetlands, 2011, 31(4): 745-756.

[32] McRae B H. Kavanagh D M. Linkage Mapper Connectivity Analysis Software. The Nature Conservancy, Seattle WA. 2011, http://www.circuitscape.org/linkagemapper.

[33] Saura S, Torné J. Conefor sensinode 2.2: a software package for quantifying the importance of habitat patches for landscape connectivity. Environmental Modelling & Software, 2009, 24(1): 135-139.

[34] Pascual-Hortal L, Saura S. Comparison and development of new graph-based landscape connectivity indices: towards the priorization of habitat patches and corridors for conservation. Landscape Ecology, 2006, 21(7): 959-967.

[35] Meurk C D, Hall G M J. Options for enhancing forest biodiversity across New Zealand′s managed landscapes based on ecosystem modelling and spatial design. New Zealand Journal of Ecology, 2006, 30(1): 131-146.

[36] 吴健生, 张理卿, 彭建, 冯喆, 刘洪萌, 赫胜彬. 深圳市景观生态安全格局源地综合识别. 生态学报, 2013, 33(13): 4125-4133.

[37] 许文雯, 孙翔, 朱晓东, 宗跃光, 李杨帆. 基于生态网络分析的南京主城区重要生态斑块识别. 生态学报, 2012, 32(4): 1264-1272.

[38] 王云才. 上海市城市景观生态网络连接度评价. 地理研究, 2009, 28(2): 284-292.

[39] 傅强, 宋军, 毛锋, 吴永兴, 姚涵, 唐剑波. 青岛市湿地生态网络评价与构建. 生态学报, 2012, 32(12): 3670-3680.

[40] 王海珍, 张利权. 基于GIS、景观格局和网络分析法的厦门本岛生态网络规划. 植物生态学报, 2005, 29(1): 144-152.

[41] Shafer C L. Nature Reserves: Island Theory and Conservation Practice. California: Smithsonian Institution Press, 1990.

[42] Gilbert-Norton L, Wilson R, Stevens J R, Beard K H. A meta-analytic review of corridor effectiveness. Conservation Biology, 2010, 24(3): 660-668.

[43] Brooker L. The application of focal species knowledge to landscape design in agricultural lands using the ecological neighbourhood as a template. Landscape and Urban Planning, 2002, 60(4): 185-210.

[44] 郑景明, 桑卫国, 马克平. 种子的长距离风传播模型研究进展. 植物生态学报, 2004, 28(3): 414-425.

Identifying and evaluating functional connectivity for building urban ecological networks

CHEN Chundi1,3,*, MEURK D. Colin2, IGNATIEVA E. Maria3, STEWART H. Glenn3, WU Shengjun1

1KeyLaboratoryofReservoirAquaticEnvironment,ChongqingInstituteofGreenandIntelligentTechnology,ChineseAcademyofSciences,Chongqing400714,China2LandcareResearch,CrownResearchInstituteNewZealand,Lincoln7608,NewZealand3LincolnUniversity,Christchurch7674,NewZealand

With rapid urbanization and industrialization, habitat fragmentation and loss are inevitable. Under these circumstances, landscape connectivity and ecological networks have become a focus of applied landscape ecology. A well-connected ecological network is believed to facilitate energy and resource fluxes, species dispersal, genetic exchange and multiple other ecological processes, and to contribute to the maintenance of ecosystem stability and integrity. Identifying and evaluating functional connectivity between habitat patches is the key step in designing and building well-connected ecological networks. Based on a review of literature on linkage identification approaches, our study combined least-cost path modeling with graph-theory based network analysis to simulate, identify, evaluate, and prioritize functional linkages. We made some modifications to conventional least-cost model and network analysis in order to reduce subjectivity and to better suit the specific conditions of urban environments. Least-cost models are commonly used to determine the movement routes of wildlife to optimize conservation of meta-populations in wild environments. Ideally, least-cost models should be parameterized with field data for a specific organism (usually a small animal); however, these data are difficult and time-consuming to collect, and this has resulted in a large number of studies relying entirely or in large part on collective expert opinion. Different experts may assign different values and therefore affect the reliability of network simulation. Therefore, we adopted the Landscape Development Intensity (LDI) index, which is a measure of human disturbance of ecosystems, to quantify the relative costs of land use/cover types. In addition, we chose not to use small mammals as the individual surrogate for designing our urban ecological network. Most studies of animal movement patterns have been conducted in continuous forest landscapes, which are very different from patchy urban environments. These are characterized by much smaller and fragmented habitat patches, surrounded by a non-living concrete matrix with various threats hostile to life. Instead, we used native trees as individual surrogates and their seed dispersal pattern, based on a field survey, for devising and simulating a functional urban ecological network. Taking Christchurch, New Zealand, as an example, our study used a climax native forest tree,Dacrycarpusdacrydioidesas a surrogate in establishing our urban ecological network. We used the LDI index to build the cost surface for a least-cost model in ArcGIS 10.0, and the observed maximum seed dispersal distance ofD.dacrydioides(1200 m) as the threshold distance for network analysis in Conefor 2.6. Under the 1200 m threshold distance, a total of 408 links were simulated in the study area. These were grouped into 10 importance grades using Hierarchical Cluster Analysis in SPSS 21.0 combined with input from decision-makers. Among these, the three most important links were between Richmond Park and Petrie Park, Hansons Reserve and Auburn Reserve, and between Centaurus Park and King George Reserve. They were identified as the cut-links in a landscape graph, i.e. removal would disconnect critical components in the landscape. Indeed, if these links were absent, the Integral Index of Connectivity (IIC) of the whole landscape would be reduced by 31.73%. Additionally, our study found that there was no linear relationship (Pearson′sr=0.078,P=0.118) between link importance value and total area of habitat connected. That is, the links between larger habitats are not necessarily more important to the network. Further studies are needed to support this finding. Overall, our case study suggests that the combination of least-cost pathway analysis and graph-theoretical algorithms is an efficient approach for simulating and prioritizing functional connectivity in urban landscapes, and might be valuable for Chinese urban ecological network planning. Furthermore, the energy-consumption based LDI index was shown to be a reliable measurement of relative cost values of land use/cover types. However, it should be pointed out that the LDI index was calculated based on western land use/cover types, which are different from those used in China. It is recommended that when being applied in China, the LDI index should be adjusted to China′s land use/cover types.

urban ecological networks; functional connectivity; native habitats; least-cost model; graph theory; native tree seed dispersal

国家自然科学基金(51408584, 41401633); 中国科学院重庆绿色智能技术研究院三峡生态环境研究海外高层次人才基地项目(Y33Z172N10); 新西兰基督城地震恢复重建规划(CO9X0309); 宁波市科技计划项目(2013A610164)

2014-02-16; < class="emphasis_bold">网络出版日期:

日期:2014-12-04

10.5846/stxb201402160263

*通讯作者Corresponding author.E-mail: chenchundi@cigit.ac.cn

陈春娣, Meurk D. Colin, Ignatieva E. Maria, Stewart H. Glenn 吴胜军.城市生态网络功能性连接辨识方法.生态学报,2015,35(19):6414-6424.

Chen C D, Meurk D. Colin, Ignatieva E. Maria, Stewart H. Glenn, Wu S J.Identifying and evaluating functional connectivity for building urban ecological networks.Acta Ecologica Sinica,2015,35(19):6414-6424.