基于生成图算法的混合WSNs的避障调度研究*

谢光前， 李春光， 潘 丰

(1.江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.常州工学院 计算机信息工程学院，江苏 常州 213000))

基于生成图算法的混合WSNs的避障调度研究*

谢光前1,2， 李春光1,2， 潘 丰1

(1.江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.常州工学院 计算机信息工程学院，江苏 常州 213000))

为了解决存在障碍物的混合无线传感器网络(WSNs)的动态传感器调度问题，构建了基于生成图的调度算法和模型。利用基于网格的技术获得了障碍物的规整化图形；根据基于生成图的算法，使得最短路径的搜索空间限制在连通图中；在实现最短避障路径的基础上，获得了动态传感器的能量有效性的调度目标。通过仿真，验证了方法的有效性。

混合无线传感器网络； 基于网格的； 生成图； 调度

0 引 言

混合无线传感器网络(WSNs)已成为当前的热点研究问题之一。在混合WSNs中，静态传感器感知目标区域的信息，并把这些信息向外传送，功能较单一。动态传感器根据静态传感器反馈过来的结果，移动到目标地区进行更深入的分析，然后进行相应的处理[1]。这里假定静态传感器的生命周期足够长，这样问题就归结为如何有效调度动态传感器，使得整个网络系统的生命周期最长,因此，整个网络系统的生命周期是由动态传感器节点能量决定的。通常只要出现一个动态传感器节点能量耗尽的情况，则意味整个网络系统生命周期的结束,所以,合理调度动态传感器的旅行路径尤为关键。关于动态传感器调度的问题，当前很多文献已经做了大量的研究[2～4],但这些研究很少考虑WSNs中存在障碍物的情况,而在实际的应用环境中，会或多或少存在障碍物。

本文针对混合WSNs存在障碍物的情况下，提出了基于生成图算法的动态传感器调度方案。

1 调度模型的建立

1.1 初始模型

在实际应用中，网络区域内环境多变，会存在大小不一，形状各异的障碍物。随着能量捕获技术的进步，这里不考虑静态传感器的能量，认为其具有足够的能量。所以,混合WSNs的生命周期由动态传感器决定，只要有一个动态传感器能量耗尽，则整个网络生命周期结束。尽可能降低动态传感器的能耗，最直接的办法是以最短路径到达目标区域。考虑到系统的复杂性，研究只考虑最简单的情况，也就是只有一个动态传感器，同时目标区域也只有一个。如图1所示，监控区域是个矩形，黑色圆点代表随机分布的静

态传感。黑色不规则图形代表障碍物，这里假定有两处障碍物。黑色实三角形S代表动态传感器的初始区域位置，而白色虚三角形t代表目标区域位置。很显然,从位置S移动到位置t的过程中存在绕行路径，此种情况求解最短路径存在一定的困难。

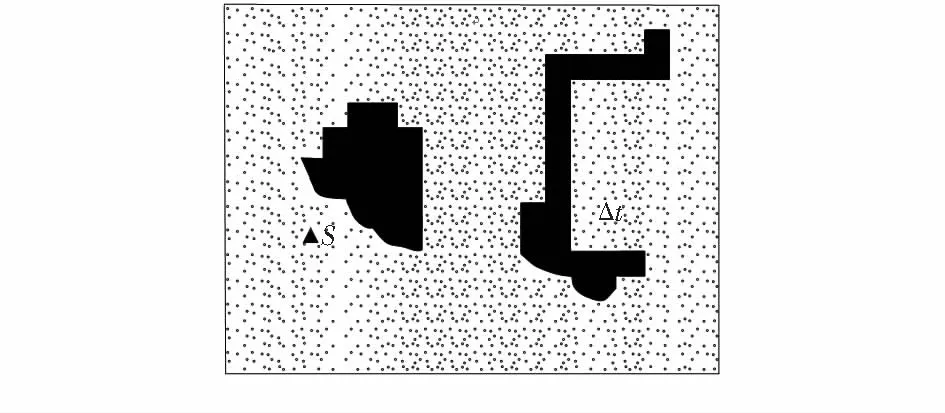
图1 系统初始调度模型Fig 1 Initial scheduling model of system

1.2 模型的网格化处理

基于网格划分技术目前已被广泛应用于分析WSNs[5]。本文研究所划分的网格单元为正方形，网格单元也是动态传感器进行信息收集与处理的基本单位。每个网格单元存在一个汇聚点位置，在此位置，可以收集网格单元中所有传感器的信息。汇聚点位置一般位于网格单元的中心，这样便于收集网格单元中所有传感器的信息。为了研究的方便，本文假定动态传感器的最小移动单位为1，并且动态传感器只能沿着水平或者垂直方向移动。图2是图1网格化的结果,其中小圆点代表每个网格单元的汇聚点位置，网格单元的边长为单位1。

图2与图1相比，很显然障碍物的边缘地带会与网格单元相交，可能只占用部分网格单元。假如:网格单元被部分占用，就认为此网格单元即为障碍物，这样障碍物就变成了比较规整的图形。图2中，动态传感器一开始位于起点黑色实三角形S所在网格单元的汇聚点位置，需要以最短路径移动到终点白色虚三角形t的汇聚点位置即可。

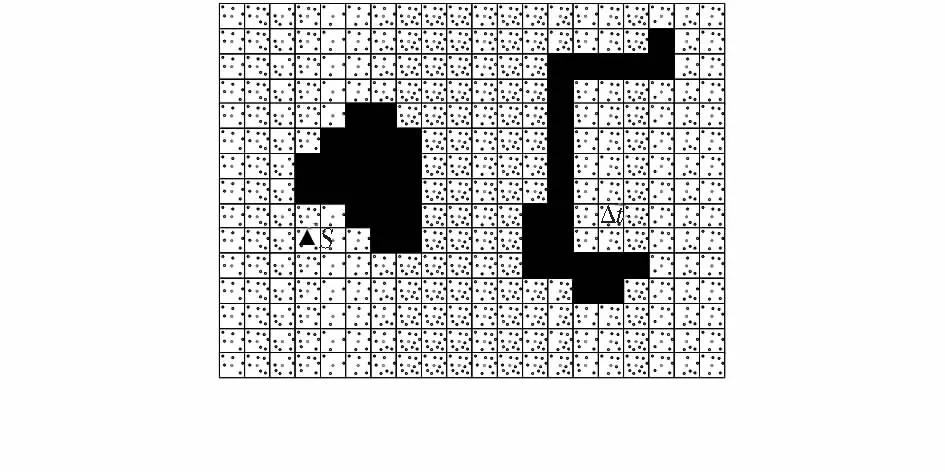
图2 系统模型网络图Fig 2 Grid graph of system model

2 基于生成图算法的调度

文献[6]提出了基于生成图算法的基本思想，并解决了最小生成树问题。动态传感器的最短移动路径问题，可转化为最小生成树问题。基于生成图算法调度的基本思想是利用线扫描技术生成可能的调度路径，并以此为基础，利用Dijkstra算法容易找到最短路径。本文基于其近似算法，对于某个确定点，对整个平面进行4等分,在不影响调度结果的前提下，使问题的求解大大简化。如图3(a)所示，黑色矩形为障碍物，障碍物的4个顶点分别为p1～p4，R1～R8是以p1～p4为原点的平面划分区域。图3(b)为动态传感器初始或目标所在位置p的平面划分区域。

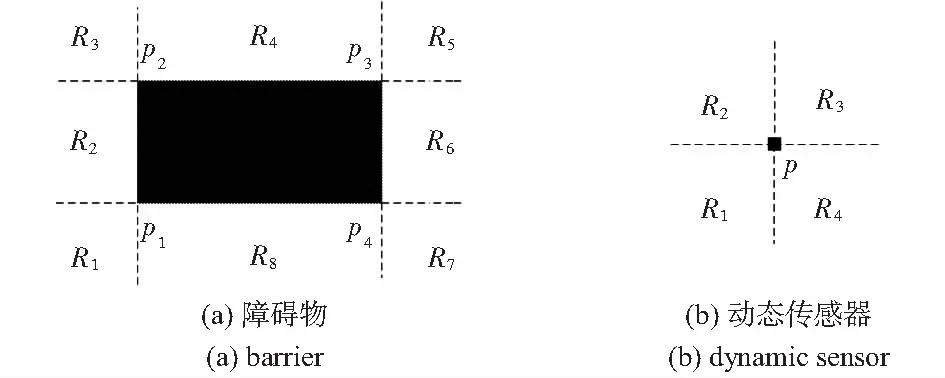
图3 生成图算法中顶点位置搜索区域划分Fig 3 Search region division for vertex in spanninggraph algorithm

利用图3的区域划分的方法，并根据算法1，生成图4。因此,本文的调度目标就转化为从生成图中找到从源点S到目标点t的最短路径。动态传感器应该沿着障碍物边线和基于算法1生成的连接线方向移动。这里需要说明的是本文的方法基于网格化基础之上的，并且动态传感器的移动只能水平或者垂直移动。所以，实际的动态传感器的移动路径不是沿着算法 1生成的连接线方向移动，而是基于连接线的Manhattan距离移动的。

图4 系统模型生成图Fig 4 Spanning graph of system model

算法1是利用线扫描技术，分别在顶点对应的各区域执行连线操作，顶点区域划分见图3，最终构建了系统模型的生成图。

算法1生成图的构建

输入:

数组Vs:顶点坐标位置，包含障碍物各顶点位置和动态传感器初始点以及目标点位置

输出:

生成图G:最终的连接图，数组Vs中各点位于连接图上

1)begin

2)数组Vs按x轴方向递增排序;

3)障碍物顶点R2，R6区域，找到该区间最短路径；

4)数组Vs按y轴方向递增排序;

5)障碍物顶点R4，R8区域，找到该区间最短路径;

6)数组Vs按x+y轴方向递增排序;

7)障碍物顶点R1，R5区域及动态传感器初始点目标点R1，R3区域，找到该区间最短路径；

8)数组Vs按y-x轴方向递增排序;

9)障碍物顶点R3，R7区域与动态传感器初始点目标点R2，R4区域，找到该区间最短路径；

10)end

3 仿真结果与分析

3.1 实验场景

实验场景如图1中所示。网络区域的大小为20×15,动态传感器的最小移动单位为1，因此,把整个网络区域划分成20×15=300个网格单元，如图2所示。实验所使用的台式机是Intel i5—2400处理器，4 GB内存和32位的Windows7系统。

3.2 评估结果

图5显示了在网格图中动态传感器的搜索空间极其最终的移动路径。其中，黑色实三角形S为起点，白色虚三角形t为终点，圆点为算法的搜索空间，一共有104个网格单元。黑色圆点为动态传感器的最终移动路径，从起点S到终点t，一共移动了23个单位。根据实验结果，很明显最终的路径也是最短路径。

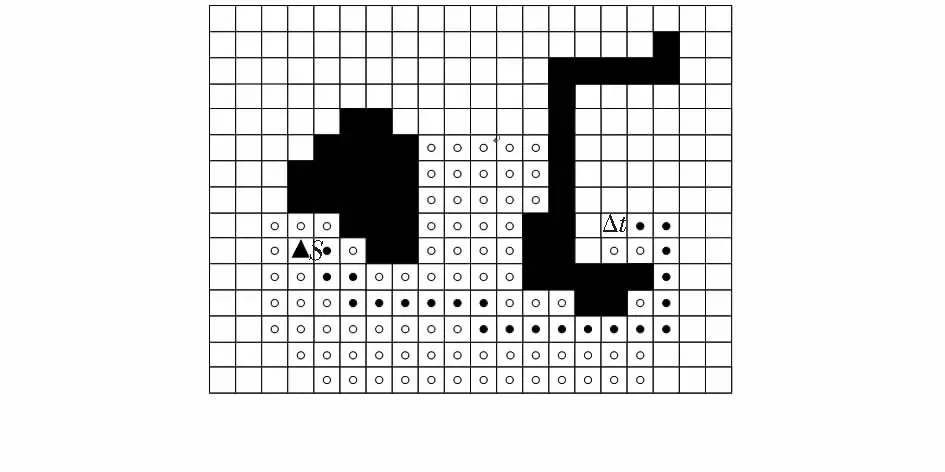
图5 网格图中动态传感器的顶点扩展Fig 5 Vertex expansion of dynamic sensor in grid graph

图6显示了在生成图中动态传感器的搜索空间及其最终的移动路径。从图形中可以看出搜索空间只占34个单元格，而最终的动态传感器也移动了23个单位，即为动态传感器的最短移动距离。与图5相比，图6的搜索空间减小了2/3，但最终动态传感器的移动距离大小一致，均为最短移动路径。

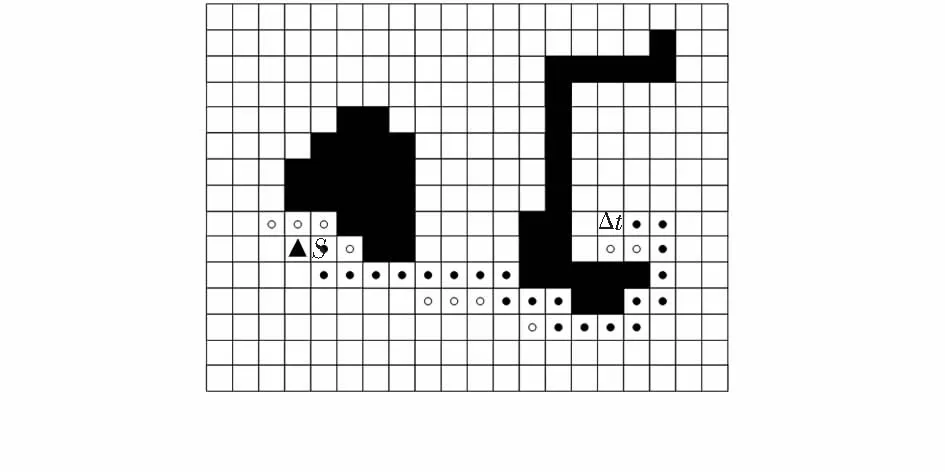
图6 生成图中动态传感器的顶点扩展Fig 6 Vertex expansion of dynamic sensor in spanning graph

表1显示了两种情形下，程序的运行时间。在网格图中，程序运行了0.112 s，而在生成图中，程序运行了0.034 s，与网格图相比，生成图程序运行时间大约减少了2/3。

根据实验结果表明:基于生成图的方法，明显效率更高，在不影响找到最短路径的前提下，减小了算法的搜索空间，提高了效率。

表1 两种模型运行时间的比较
Tab 1 Comparison of run time of two models

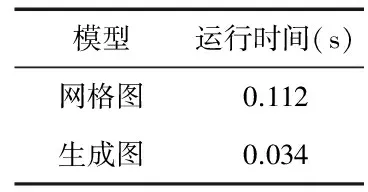
模型运行时间(s)网格图0．112生成图0．034

4 结 论

本文提出了具体的实现方案，将问题的求解范围局限于实现的生成图中，从而减小了搜索空间，提高了搜索效率。最终找到了最短路径，提高了网络的生命周期。本文只研究了一对一这种最基本的情形，即一个动态传感器对应一个目标区域。

[1] Gu Y,Ji Y,Li J,et al.ESWC:Efficient scheduling for the mobile sink in wireless sensor networks with delay constraint[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(7):1310-1320.

[2] Wang Y C,Peng W C,Tseng Y C.Energy-balanced dispatch of mobile sensors in a hybrid wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2010,21(12):1836-1850.

[3] Wang Y C.A two-phase dispatch heuristic to schedule the movement of multi-attribute mobile sensors in a hybrid wireless sensor networks[J].IEEE Transactions on Mobile Computing,2014,13(4):709-722.

[4] Shwetha G K,Sagarika B,Jithendranath M.Energy balanced dispatch of mobile sensors in hybrid wireless sensor networks with obstacles[J].IOSR Journal of Computer Engineering,2012,2(1):47-51.

[5] Peng H,Chen Y W.Energy consumption bounds analysis and its applications for grid-based wireless sensor networks[J].Journal of Network and Computer Applications,2013,36(1):444-451.

[6] Zhou H,Shenoy N,Nicholls W.Efficient spanning tree construction without Delaunay triangulation[J].Information Processing Letter,2002,81(5):271-276.

Research on obstacle avoidance scheduling based on spanning graphs algorithm for hybrid WSNs*

XIE Guang-qian1,2, LI Chun-guang1,2, PAN Feng1

(1.Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi 214122,China; 2.College of Computer and Information Engineering,Changzhou Institute of Technology,Changzhou 213000,China)

To solve scheduling problem of dynamic sensors in hybrid wireless sensor networks(WSNs)with obstacles，a scheduling algorithm and model based on spanning graphs is constructed.Regularization shape of obstacles is obtained by grid-based techniques;according to algorithm based on spanning graphs,search space of the shortest path is restricted within connection graphs;a goal of energy-efficient scheduling for dynamic sensors is achieved,on the basis of realizing the shortest path of obstacle avoidance.Through simulation,the effectiveness of the method is verified.

hybrid WSNs; grid-based; spanning graph; scheduling

10.13873/J.1000—9787(2015)12—0019—03

2015—03—15

国家自然科学基金资助项目(61273131)

TP 393

： A

： 1000—9787(2015)12—0019—03

谢光前(1977-)，男，安徽安庆人，博士研究生，主要从事无线传感器网络、智能控制等方面的研究。