Direction estimation for two steady targets in monopulse radar

Zhenxing Lu,Yunjie Li,and Meiguo Gao

1.School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China;

2.The 54th Research Institute,China Electronics Technology Group Corporation,Shijiazhuang 050081,China

Direction estimation for two steady targets in monopulse radar

Zhenxing Lu1,2,Yunjie Li1,*,and Meiguo Gao1

1.School of Information and Electronics,Beijing Institute of Technology,Beijing 100081,China;

2.The 54th Research Institute,China Electronics Technology Group Corporation,Shijiazhuang 050081,China

Traditional monopulse radar cannot resolve two targets present in one range and Doppler cell by means of the monopulse ratio.A novel algorithm is proposed to estimate the directions of two steady targets with two pulses.The algorithm has a closedform expression and its variance is derived at high signal-to-noise ratios(SNRs).Furthermore,the pulse pair selection criterion and the estimation method with multiple pulses are given.Finally,some numerical results are shown to validate the proposed algorithm and the effect of slight target fuctuations is tested.

direction estimation,two unresolved targets,monopulse radar.

1.Introduction

In radar signal processing,the amplitude comparison monopulse is commonly used to determine the direction of a target by the real part of the monopulse ratio.However,in the presence of two targets within the mainlobe of a monopulse radar,if we are not able to resolve them in range or Doppler cells,the monopulse ratio does not indicate any of the two directions.In this case,the monopulse ratio varies depending on the amplitude ratio and the relative phase of the two target signals in the sum channel.

For different statistical types of targets,the mean and the variance of the monopulse ratio have been presented in[1]. If the amplitudes of the two target signals are steady and the phase difference between them is uniformly distributed in[0,2π],we can obtain the direction of the“larger”target by averaging the monopulse ratio output[2,3].In this situation,an approach was proposed in[4]to attain the midpoint of the two targets with two pulses.For two Rayleigh targets,the average monopulse ratio would represent the centroid of the two targets.An algorithm based on the method of moments was developed in[5,6]to estimate the directions with known or estimated relative radar cross section(RCS).Wang[7]has derived the maximum likelihood (ML)solution of the directions of two Rayleigh targets. Both methods in[5]and[7,8]were based on the statistical characteristics of RCSs,and required suffcient samples with Rayleigh distributed amplitudes.To resolve two targets with one snapshot,an approach was given in[9,10] using an additional difference-difference channel,but for targets with the same elevation(azimuth)angle,the azimuth(elevation)angles cannot be resolved.If a sensor array is available,the spatial spectrum estimation algorithms [11–18]can be used to resolve two or more non-coherent targets.Other methods to detect and track two or more unresolved targets can be found in[19–25].

In many scenarios,the amplitudes of two target signals are steady between pulses with a short interval,but the relative phases are different.For example,if a monopulse radar seeker working at 18 GHz moves from point(0 m, 2 000 m)to point(0 m,1 995 m)in one plane with one target at(0 m,0 m),the other from(100 m,0 m)to (99 m,0 m),and the two targets are both steady active sources or Swerling I targets whose RCSs do not fuctuate between the two instants,the amplitude changes of the two incident signals will be negligible but the relative phase will change about 5.2π(for active sources)or 10.4π(for Swerling I targets),respectively.

To acquire the two directions,Sherman[26,27]provided fve equations from two pulses:four from the real parts and imaginary parts of the monopulse ratios,the rest from the sum signals.He mentioned an algebraic-graphical method using computer program to obtain the angles of the two targets,but did not provide the closed-form solutions.In[28],the authors gave four different equations directly from the sum and difference signals at two pulses instead of the monopulse ratios.Based on these equations, closed-form solutions for the two directions were derived. However,both methods in[27]and[28]did not consider the noise components in the sum and difference channels and their performance under the presence of noise was unknown either.In the target tracking of a monopulse radar, the statistics of direction estimation are very important forthe tracking algorithms such as Kalman fltering[29].To make better use of these estimations,their statistic performance has to be studied.From[28]we know that the estimation has a very complicated nonlinear expression.It is very diffcult to derive the probability density function (PDF)of the solution even if the noise components in the sum and difference channels are both Gaussian distributed. Based on the frst-order Taylor series expansion of the solution,the variance of the direction estimation is derived at high signal-to-noise ratios(SNRs)in this paper.We will see that,besides the SNR and target position,the variance of the estimation still depends on the phase difference of the target echoes or the power difference between the two pulses.This can also help us to select the best pulse pair to resolve the two targets when more than two pulses are obtained.

2.Direction estimation for two targets in monopulse radar

2.1Signal model

When two steady targets A and B are present in the mainlobe of a monopulse radar,let θAand θBrespectively be the off-boresight angles of A and B.Regardless of the noise in the receiver,the signals in the sum and difference channels are given by

and

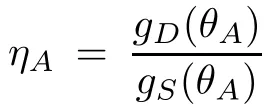
In this case,the monopulse ratio can be written as

Let SB/SA=kejφ,where k denotes the amplitude ratio of SBand SA,and φ denotes the relative phase of SBand SA.The real part of the monopulse ratio can be expressed as follows:

For two steady targets A and B,k can be treated as a constant and φ changes in some scenarios as illustrated in Section 1.In this case,the monopulse ratio will vary as φ changes.However,it is not easy to obtain the two directions directly from the monopulse ratio.

2.2Closed-form solutions to resolve the two targets

Assuming the amplitudes of SAand SBare constant and the phase difference φ varies between pulses,we can fnd two pulses with the same k and different φ.Now,instead of calculating the monopulse ratios,we can write the expressions of the sum and difference signals at pulses 1 and 2 directly as follows:

where SAi= aAejϕAi,DAi= aAηAejϕAi,SBi= aBejϕBi,DBi=aBηBejϕBi,i=1,2,in which aAand aBdenote the amplitudes of signals from A and B respectively in the sum channel,and ϕAiand ϕBidenote the phases of signals from A and B respectively at pulse i.

From(5)–(8)we have

Therefore,we can obtain ηAand ηBfrom the same equation

Equation(11)can be expressed as

where Re(·)and Im(·)denote the real part and the imaginary part,respectively.Re(S10),Im(S10),Re(D10), Im(D10),Re(S20),Im(S20),Re(D20)and Im(D20)can be obtained directly from the in-phase and quadrature components of the sum and difference signals.

Let

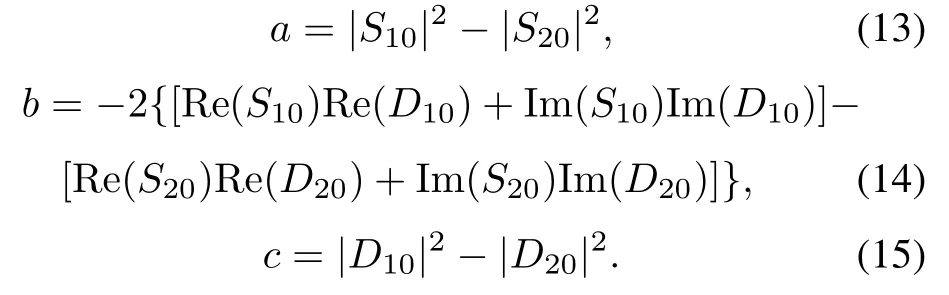
Equation(12)can be rewritten as

If ηA＞ηB,we can derive

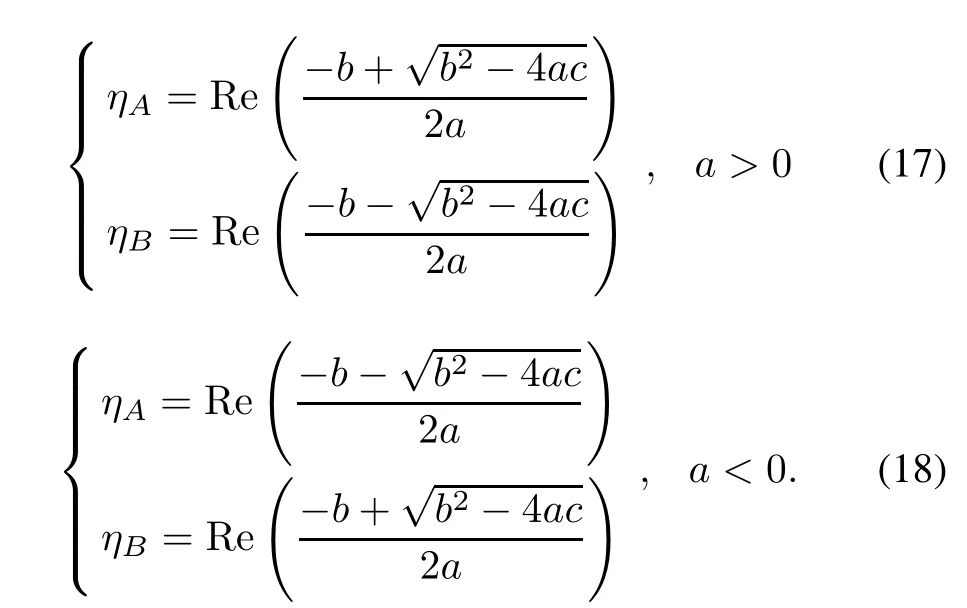
2.3Remark on the solutions

From(5)–(8)and(13)–(15)we have

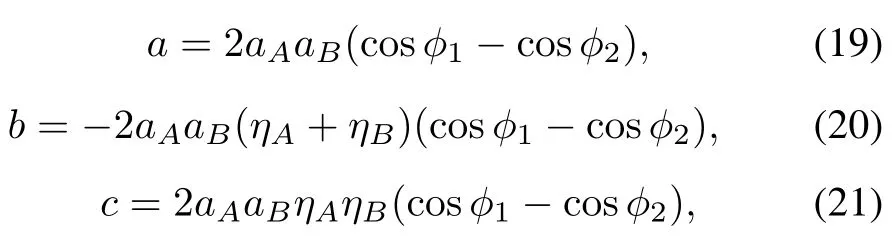
where φ1=ϕB1−ϕA1and φ2=ϕB2−ϕA2.

When cosφ1−cosφ2/=0,(16)can be rewritten as

It is obvious that ηAand ηBare the solutions of(22).

If cosφ1−cosφ2=0,which means φ1=φ2or−φ2and the two pulses have the same amplitude in the sum channel,we have a=b=c=0 in(16).In this case,we cannot get the expected solutions from(17)and(18).

3.Performance analysis

3.1Estimation variances at high SNRs

Section 2 has derived closed-form expressions for the directions of two steady targets in the noiseless monopulse model.In the case of φ1=φ2or−φ2,the two targets cannot be resolved from(17)and(18).Although the probability of φ1=φ2or−φ2is very little,the performance of the proposed method still becomes worse when φ1is closer to φ2or−φ2in the presence of noise,as the power difference a is very little and noise components will dominate the denominator in(17)and(18).Next we will derive the variances of the proposed method.

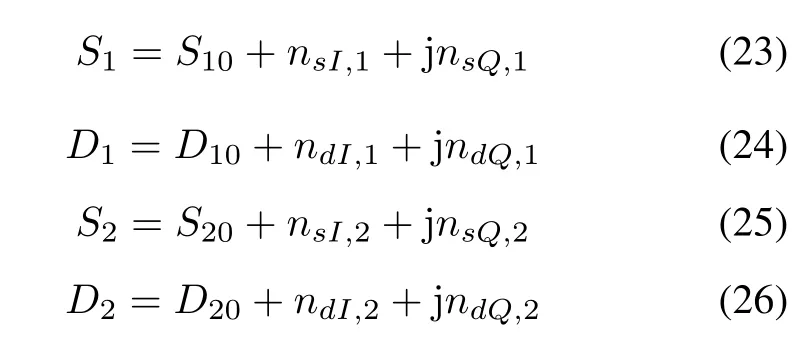
In the presence of noise,the sum and difference signals can be written as where nsI,iand nsQ,i(i= 1,2)are the in-phase and quadrature components of the noise in the sum channel at pulse i,while ndI,iand ndQ,iare the in-phase and quadrature components of the noise in the difference channel respectively.As in[7],we assume that the noise components nsI,i,nsQ,i,ndI,iand ndQ,iare independent and Gaussian distributed variables with zero-mean and variances

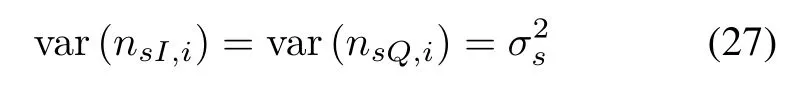
and

where i=1,2.

Inserting(23)–(26)into(13)–(15)and(17)–(18),we fnd that the expressions of(17)and(18)are very complicated.It is very diffcult to derive the PDFs and the variances of the estimations.

Like the analysis in[30]and[31],we assume that the noise terms higher than the second order in(17)or(18) can be ignored at high SNRs.Then the estimate of ηAcan be written as

where the estimation error is approximated by

Therefore,

Following(13)–(15),(17)–(19)and(21),we have

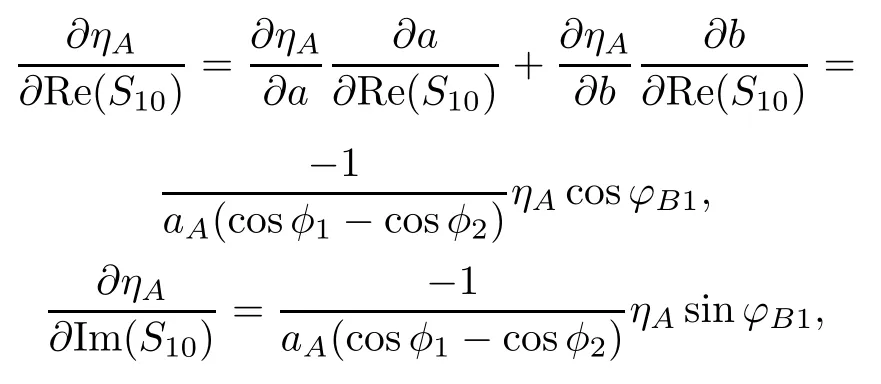
Then we can derive

In the same way,we can also derive

If the sum channel and the difference channel have the same noise power 2σ20,i.e.σ2s=σ2d=σ20,the estimation variances can be written as

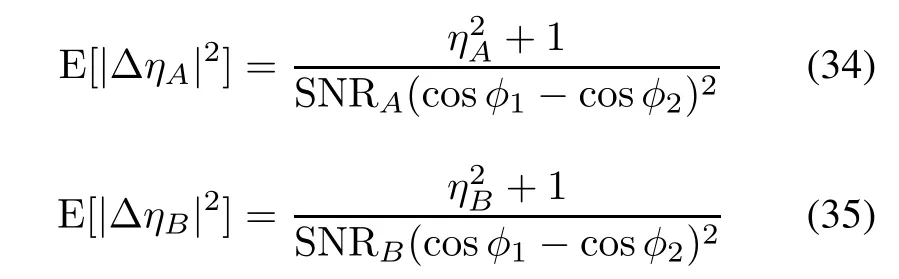
3.2Pulse pair selection from multiple pulses

From(34)and(35),we can see that the estimation variances are inversely proportional to the SNRs and(cosφ1−cosφ2)2.If|cosφ1−cosφ2|=2 is satisfed,the proposed algorithm will have the smallest variance(η2+1)/4SNR. Although φ1and φ2are not known and not under our control in real life,we still hope to select the best pulse pair when multiple pulses are received.

According to(13)and(19),cosφ1−cosφ2is proportional to the power difference between pulse 1 and pulse 2 in the absence of noise.This is approximately true at high SNRs.

In the monopulse radar,a pulse train with more than two pulses is usually employed.We assume that the two directions do not change during these pulses.In this case,we can select the pulse pair with the largest power difference from the received pulse train to obtain the best performance with the proposed two-pulse method.

It should be noted that the‘pulse’here can also be a coherent processing interval(CPI)if the targets are steadily or slowly fuctuating so that the variation of their RCSs can be ignored between two CPIs.

3.3Direction estimation with multiple pulses

Assuming that we have 2N pulses received,then N independent pulse pairs can be selected from the 2N pulses. Denote the power difference of the pth pulse pair in the sum channel by ap.From(19),(34)and(35),we can write the estimation variances of the pth pulse pair as

and

Since not every pulse pair has the same power difference,the estimation variances of them are also different. To make a better estimation with multiple pulses,the best linear unbiased estimator(BLUE)[32]can be used.

We can see that(38)and(39)have a similar form with the ML angular estimator[33]for Rayleigh fuctuating targets,which is widely used in monopulse radar.

Strictly speaking,(38)and(39)are not BLUEs,because ˆηA,pandˆηB,pfrom(17)and(18)are biased as traditional monopulse ratios.Fortunately,the biases of(17)and(18) are very small for high SNRs as shown in Section 4.

According to the theory of BLUE[32],the variances of (38)and(39)can be written as

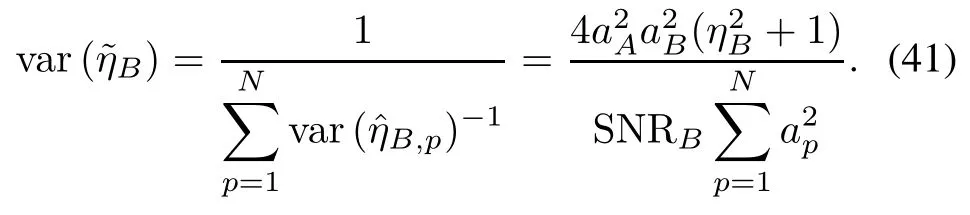
4.Simulations and discussions

We test the performance of the proposed two-pulse algorithm by numerical simulations where we assume that

Fig.1 Bias ofˆηAversus φ2

Fig.3 RMSE ofˆηAversus φ2

We can see that the algorithm has the best performance when φ2is close to 180°.In this case,the RMSEs are smaller than those of traditional monopulse ratios with only one target present(by simulation it can be shown that RMSEs of traditional monopulse ratios are 0.073,0.023 and 0.007 for SNR=20,30,40 dB respectively).SimiaB=aA=1,ηA=0.15 and ηB=−0.2.The sum channel and the difference channel have the same noise power. The two target signals have the same phase at pulse 1,i.e. φ1=0°.

4.1Biases and root mean square errors versus phase differenceφ2

Fig.2 Bias ofˆηBversus φ2

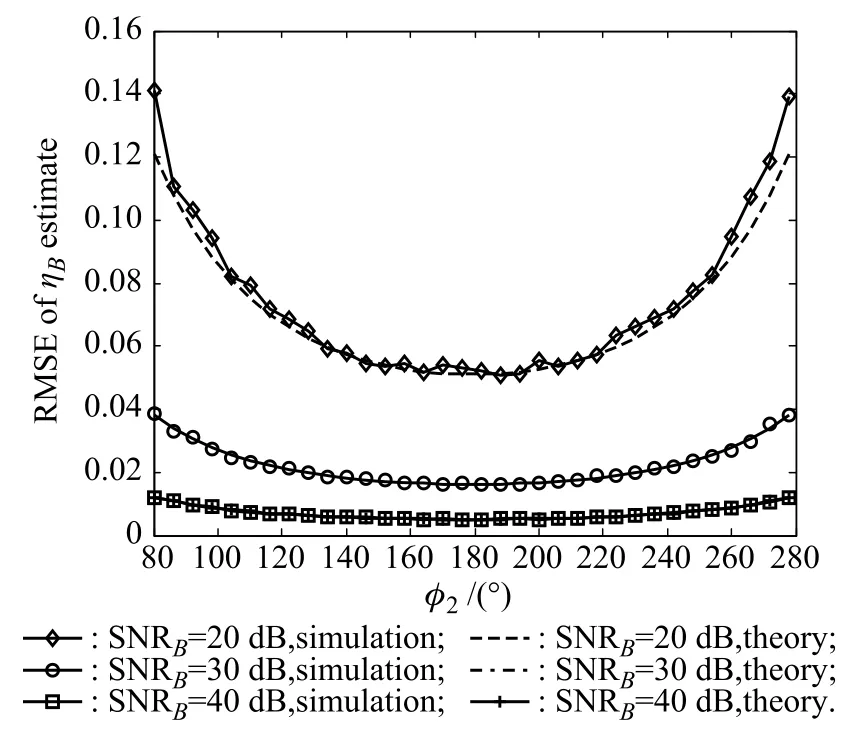
Fig.4 RMSE ofˆηBversus φ2

Under different SNR s and φ2,Monte-Carlo simulations are conducted by 1 000 independent trials.Figs.1–4 show the biases and root mean square errors(RMSEs)ofˆηAandˆηBin the case that φ2varies from 80°to 280°(when φ2gets closer to φ1the performance will become worse). lar to the analysis of Section 3,the variance of Re(D/S) can be approximated by(η2+1)/2SNR in the single target case,which is obviously larger than(34)or(35)in the case of φ1=0°and φ2=180°.For φ2=80°or 280°, the RMSEs are only about twice as many as those of traditional monopulse ratios.

4.2RMSEs versus the power differencea

Fig.5 and Fig.6 also give the RMSEs ofˆηAandˆηBversus the power difference a(see(13))between the two pulses.It is shown that the RMSEs will decrease as the power difference a increases and the simulation results are very close to the theory values.At low SNRs,the variance of the algorithm might be a little larger than the theory value(see Figs.3–6).This is because the noise terms higher than the second order are neglected in the derivation of(34)and (35).

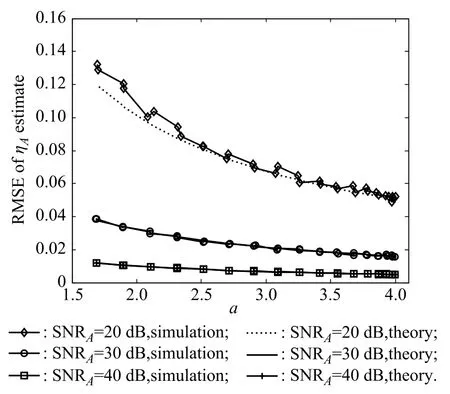
Fig.5 RMSE ofˆηAversus a

4.3Comparison with Sherman’s method

The proposed two-pulse method and the Sherman’s method[27]have the same signal model,so the results of them are identical to each other if the noise components are not considered.Through simulation,we fnd that the two methods still have the same results under the presence of noise as shown in Fig.7 and Fig.8.However,the proposed method has closed-form solutions while the Sherman’s method does not.

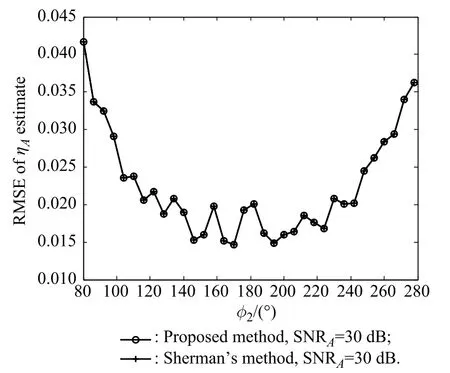
Fig.7 RMSE ofˆηAcomparison with Sherman’s method

Fig.8 RMSE ofˆηBcomparison with Sherman’s method

It should be noted that in Fig.7 and Fig.8,only 100 Monte-Carlo simulations are conducted.This is because the Sherman’s method needs to solve a very complex nonlinear equation,which is time consuming.

4.4Test under target fuctuations

In the following simulations,we will consider slight fuctuations of the two targets.Let aAand aBuniformly distribute in[1,1.2],and keep the other conditions the same as Figs.1–4.The biases and RMSEs from 1 000 Monte-Carlo runs are given in Figs.9–12.Comparing Figs.9–12 with Figs.1–4,we can observe that both the biases and RMSEs become larger at high SNRs.If the fuctuations of aAand aBare denoted by ΔaAand ΔaBin(5)–(8),i.e. replacing aAand aBwith aA+ΔaAand aB+ΔaBrespectively,all the terms with ΔaAand ΔaBcan be treated as noise.When the terms produced by the fuctuations are larger than the additional noise,the performance of the proposed algorithm will become worse.In our simulations,ΔaAandΔaBare proportional to aAand aB,so the larger SNRs are,the more obvious the effect of fuctuations willbe.

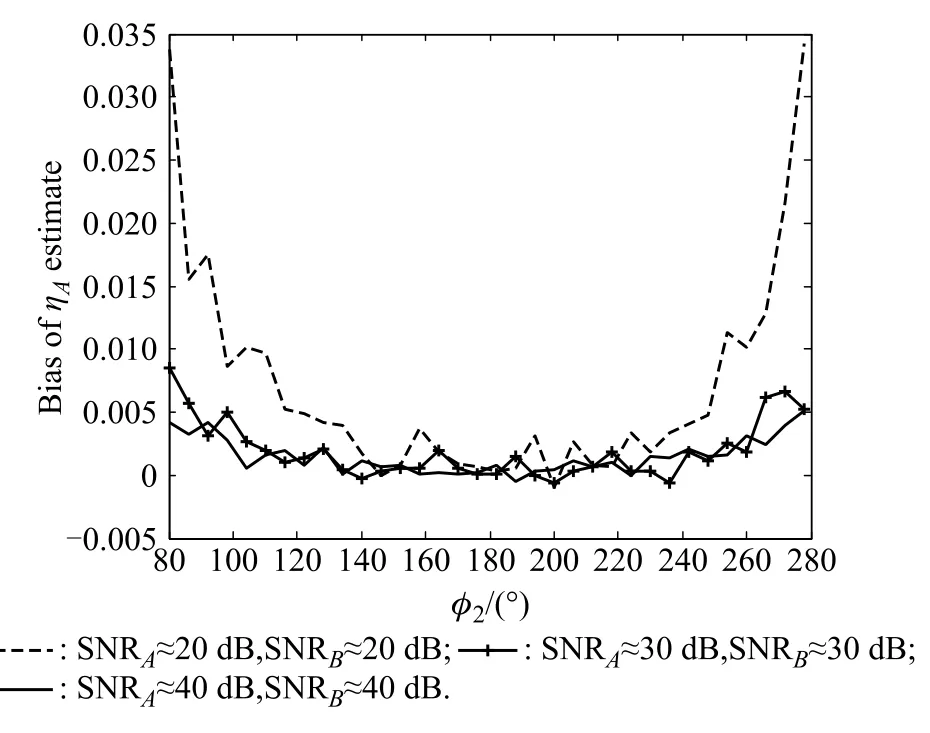
Fig.9 Bias ofˆηAversus φ2,with aAand aBuniformly distributed in[1,1.2]

Fig.10 Bias ofˆηBversus φ2,with aAand aBuniformly distributed in[1,1.2]

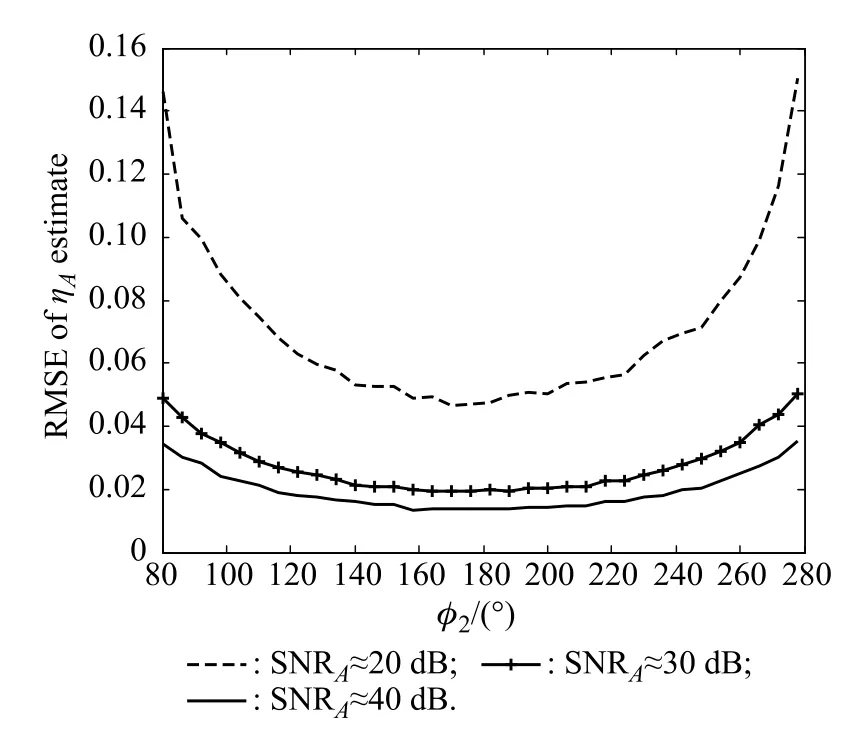
Fig.11 RMSE ofˆηAversus φ2,with aAand aBuniformly distributed in[1,1.2]

Fig.12 RMSE ofˆηBversus φ2,with aAand aBuniformly distributed in[1,1.2]

5.Conclusions

Under the circumstances of two unresolved steady targets emerging in the mainlobe of a monopulse radar,we have found closed-form solutions for the directions of the two targets with the real parts and the imaginary parts of the sum and the difference signals at two pulses.It is demonstrated that the variance of the direction estimation is inversely proportional to the SNR and the power difference between the two pulses at high SNRs.Therefore,in the case of multiple pulses,the pulse pair with the largest power difference should be selected.The performance of the new algorithm is verifed by numerical simulation and the effect of slight target fuctuations is considered.

[1]M.B.Schober.Angular mean and variance for selected twosource radar-target combinations.IEEE Trans.on Aerospace and Electronic Systems,2002,38(7):1038–1046.

[2]I.Kanter.Varieties of average monopulse responses to multiple targets.IEEE Trans.on Aerospace and Electronic Systems, 1981,17(1):25–28.

[3]Y.M.Li,F.H.Wang,Z.T.Huang,et al.Performance of antiradiation seeker in counteracting three uncorrelated decoys. Systems Engineering and Electronics,2011,33(3):500–510. (in Chinese)

[4]R.S.Berkowitz,S.M.Sherman.Information derivable from monopulse radar measurements of two unresolved targets. IEEE Trans.on Aerospace and Electronic Systems,1971,7(9): 1011–1013.

[5]W.D.Blair,M.Brandt-Pearce.Monopulse DOA estimation of two unresolved Rayleigh targets.IEEE Trans.on Aerospace and Electronic Systems,2001,37(4):452–469.

[6]W.D.Blair,G.A.Watson,M.Brandt-Pearce.Monopulse tracking of two unresolved Rayleigh targets.Proc.of the SPIE Conference on Signal and Data Processing of Small Targets, 1997:452–463.

[7]Z.Wang,A.Sinha,P.Willett,et al.Angle estimation for two unresolved targets with monopulse radar.IEEE Trans.on Aerospace and Electronic Systems,2004,40(7):998–1019.

[8]Z.Y.Song.H.T.Xiao,Q.Fu,et al.A novel approach tojointly estimate of the DOA of the target and decoy within the radar beam.Journal of National University of Defense Technology,2012,34(5):96–101.

[9]Y.Zheng,S.M.Tseng,K.B.Yu.Closed-form four-channel monopulse two-target resolution.IEEE Trans.on Aerospace and Electronic Systems,2003,39(7):1083–1089.

[10]Y.Zheng,S.M.Tseng.A closed form solution for two-target direction of arrival using four-channel monopulse.Proc.of the Thirty-ffth Asilomar Conference on Signals,Systems and Computers,2001:381–385.

[11]W.J.Si,X.C.Si,Z.Y.Qu.New method for passive radar seeker to antagonize non-coherent radar decoy.Journal of Systems Engineering and Electronics,2010,21(3):397–403.

[12]Y.Wang,T.Fu,M.G.Gao,et al.DOA estimation by exploiting spatial and Doppler sparsity.Proc.of the IET International Radar Conference,2013:1–4.

[13]C.Qian,L.Huang,H.C.So.Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling.IEEE Signal Processing Letters,2014,21(2):140–144.

[14]A.Khabbazibasmenj,A.Hassanien,S.A.Vorobyov,et al.Effcient transmit beamspace design for search-free based DOA estimation in MIMO radar.IEEE Trans.on Signal Processing, 2014,62(6):1490–1500.

[15]P.Heidenreich,A.M.Zoubir,M.Rubsamen.Joint 2-D DOA estimation and phase calibration for uniform rectangular arrays.IEEE Trans.on Signal Processing,2012,60(6):4683–4693.

[16]B.Liao,Z.G.Zhang,C.Shing-chow.DOA estimation and tracking of ULAs with mutual coupling.IEEE Trans.on Aerospace and Electronic Systems,2012,48(1):891–905.

[17]Z.Q.He,Q.H.Liu,L.N.Jin,et al.Low complexity method for DOA estimation using array covariance matrix sparse representation.Electronics Letters,2013,49(3):228–230.

[18]N.Hu,Z.F.Ye,X.Xu,et al.DOA estimation for sparse array viasparse signal reconstruction.IEEE Trans.on Aerospace and Electronic Systems,2013,49(2):760–773.

[19]X.Zhang,P.K.Willett,Y.Bar-Shalom.Monopulse radar detection and localization of multiple unresolved targets via joint bin processing.IEEE Trans.on Signal Processing,2005, 53(4):1225–1236.

[20]X.Zhang,P.K.Willett,Y.Bar-Shalom.Detection and localization of multipleun resolved extended targets via monopulse radar signal processing.IEEE Trans.on Aerospace and Electronic Systems,2009,45(2):455–472.

[21]N.Nandakumaran,A.Sinha,T.Kirubarajan.Joint detection and tracking of unresolved targets with monopulse radar.IEEE Trans.on Aerospace and Electronic Systems,2008,44(4): 1326–1341.

[22]F.Bandiera,M.Del Coco,G.Ricci.A multitarget rangeazimuth tracker for maritime applications.Proc.of the 5th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing,2013:25–28.

[23]P.N.Pathirana,S.C.K.Herath,A.V.Savkin.Multitarget tracking via space transformations using a single frequency continuous wave radar.IEEE Trans.on Signal Processing, 2012,60(10):5217–5229.

[24]F.Bandiera,M.Mancino,G.Ricci.Localization strategies for multiple point-like radar targets.IEEE Trans.on Signal Processing,2012,60(12):6708–6712.

[25]L.F.Zhou,M.Zhang,N.Zhao.Angle estimation for two unresolved Swerling I targets in monopulse radar.Proc.of the International Conference on Microwave and Millimeter Wave Technology,2010:1622–1625.

[26]S.M.Sherman.Complex indicated angles applied to unresolved radar targets and multipath.IEEE Trans.on Aerospace and Electronic Systems,1971,7(1):160–170.

[27]S.M.Sherman,D.K.Barton.Monopulse principles and techiques.2nd ed.London:Artech House Publisher,2011.

[28]Z.X.Lu,M.G.Gao,H.Q.Jiang,et al.Closed-form solutions for directions of two steady targets with two pulses in monopulse radar.Proc.of the IEEE Radar Conference,2012: 74–78.

[29]W.D.Blair,M.Brandt-Pearce.Statistical description of monopulse parameters for tracking Rayleigh targets.IEEE Trans.on Aerospace and Electronic Systems,1998,34(2): 597–612.

[30]Y.T.Chan,K.C.Ho.A simple and effcient estimator for hyperbolic location.IEEE Trans.on Signal Processing,1994, 42(8):1905–1915.

[31]K.C.Ho.Bias reduction for an explict solution of source localization using TDOA.IEEE Trans.on Signal Processing,2012, 60(5):2101–2114.

[32]S.M.Kay.Fundeamentals of statistical signal processing. Beijing:Publishing House of Electronics Industry,2003.

[33]E.Mosca.Angle estimation in amplitude comparison monopulse systems.IEEE Trans.on Aerospace and Electronic Systems,1969,5(2):205–212.

Biographies

Zhenxing Lu was born in 1984.He received his B.S.,M.S and Ph.D.degrees from Shandong University,Harbin Institute of Technology and Beijing Institute of Technology in 2005,2007 and 2014, respectively.Now he is an engineer of the 54th Research Institute of China Electronics Technology Group Corporation.His research interests include radar signal processing and adaptive beamforming. E-mail:lzx-1984@163.com

Yunjie Li was born in 1975.He received his B.S., M.S.and Ph.D.degrees in electronic engineering from the Beijing Institute of Technology in 2005. He became a lecturer from the school of Information and Electronic Engineering at Beijing Institute of Technology in 2005 and now is an associate researcher.His primary research interests include radar systems,radar signal processing and radar electronic reconnaissance.

E-mail:liyunjie@bit.edu.cn

Meiguo Gao was born in 1965.He received his B.S.,M.S.and Ph.D.degrees in electronic engineering from the Beijing Institute of Technology.He became a lecturer from the School of Information and Electronic Engineering at Beijing Institute of Technology in 1994 and now is a full professor.His primary research interests include real time signal processing,and radar electronic reconnaissance.

E-mail:meiguo g@bit.edu.cn

10.1109/JSEE.2015.00009

Manuscript received November 22,2013.

*Corresponding author.