EMMD-Prony approach for dynamic validation of simulation models
Yongxing Chen,Xiaoyan Wu,Xiangwei Bu,and Ruiyang Bai
Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China
EMMD-Prony approach for dynamic validation of simulation models
Yongxing Chen*,Xiaoyan Wu,Xiangwei Bu,and Ruiyang Bai
Air and Missile Defense College,Air Force Engineering University,Xi’an 710051,China
Model validation and updating is critical to model credibility growth.In order to assess model credibility quantitatively and locate model error precisely,a new dynamic validation method based on extremum feld mean mode decomposition(EMMD)and the Prony method is proposed in this paper.Firstly,complex dynamic responses from models and real systems are processed into stationary components by EMMD.These components always have defnite physical meanings which can be the evidence about rough model error location.Secondly,the Prony method is applied to identify the features of each EMMD component.Amplitude similarity,frequency similarity,damping similarity and phase similarity are defned to describe the similarity of dynamic responses. Then quantitative validation metrics are obtained based on the improved entropy weight and energy proportion.Precise model error location is realized based on the physical meanings of these features.The application of this method in aircraft controller design provides evidence about its feasibility and usability.
dynamic validation,extremum feld mean mode decomposition(EMMD),Prony method,error location,model updating.
1.Introduction
With the increasing role of modeling and simulation in engineering practice,a model is often used to represent a physical system under specifc assumptions[1].Before a model can be used for real world applications,model verifcation validation and accreditation(VV&A)must be conducted to quantify its validity and predictive capabilities.Model validation is the key job in the VV&A.It is always defned as the process of determining the degree that a model can represent the real world[2].With the development of validation technology,there is a growing recognition that model validation is not merely a process to collect evidence about model credibility,but also a process to collect information from validation results to improve the model by possible means[3,4].In view of advantages brought by dynamic data in revealing system information, dynamic validation becomes the hotspot in model validation.
The dynamic outputs of engineering systems are always non-stationary time series.It brings especially challenges to model validation of a dynamic system[5,6].Traditional methods,such as Theil’s inequality coeffcient(TIC)[7] and grey relational analysis[8,9],are always qualitative. They are commonly used for model comparison.Because of ignoring other information hidden in the dynamic response,their results can not provide evidence about model validity and guide model updating effectively.Recently, dynamic validation methods that can provide quantitative results for decision making about model application have been developed suffciently[10,11].These methods always contain two elements as feature extraction and quantitative assessment[12].Feature extraction aims to reduce the dimensionality of time series data and improve the model validation effciency.Quantitative assessment is a quantitative measure of agreement between the two sets of feature data.Different features have been used in these methods,such as peak response,phase,and slope,root mean square error of time series,principal components,and frequency response functions[13–15].Geers[16]proposed a method to evaluate the difference between the two dynamic responses in the magnitude and the phase.Then, the phase form of this metric was improved by Russell [17].Although the quantitative validation result is important,model error location is more important when its result is undesirable.It requires the features used in model validation must have specifc physical meanings.Error assessment of response time histories(EARTH)[18]is developed in recent years for dynamic validation.It provides three independent errors associated with the key features of the functional responses,such as phase error,magnitude error,and slope error.These features always have defnitephysical meanings.They can provide some useful information for model error location.However,the ranges of the three EARTH errors are quite different,so it is diffcult for engineers to interpret how good or how bad a model is based on these raw error data.Zhan et al.[19]proposed an enhanced EARTH metric(EEARTH)to translate the original three EARTH errors into one intuitive score between 0 and 100%,so that it can be easily interpreted by engineers.Although it solves the problem existing in EARTH, it is computational-consuming as it needs warping data after each EARTH error.And it also leads to information loss of the dynamic response.Furthermore,subject matter experts(SMEs)play an important role in the implementation of EEARTH.It brings subjective factors to the validation result inevitably which makes its result suspectable. Although validation methods based on feature extraction have been researched a lot,some features that have remarkable infuence on the system response,such as damping, are always ignored.
The Prony method can represent uniformly simple data into linear combination of exponentials[20,21].It can estimate a the physical features,such as frequency,amplitude,damping and phase,of dynamic responses easily. It provides new method for model validation[22].However,the Prony method is used for stationary signals and sensitive to noise.It cannot be applied directly to dynamic responses which are always nonlinear,nonstationary time series.Some authors[23,24]proposed a method for signal analysis based on empirical mode decomposition(EMD)and the Prony method.These methods apply EMD to adaptively flter the noise of the input signals before the Prony method is carried out.It improves the antinoise ability of the Prony method effectively.However, EMD results are usually unreliable because of serious endpoint effects[25].Extremum feld mean mode decomposition(EMMD),based on EMD and adaptive time varying flter decomposition(ATVFD),is a new adaptive signal processing method for nonlinear,nonstationary signals [26,27].It can decompose complex signals into the intrinsic mode function(IMF)and the residues which always have specifc physical meanings.Different from EMD that only use the extreme points,EMMD calculates the mean value by all data between extreme points.It can eliminate the direct current hidden in local data and make the IMF suit the constraints better.
In this paper,a dynamic validation method is proposed based on EMMD and Prony method.EMMD is used to process the dynamic response into stationary components and flter noise.Its result contains two kinds of elements. One is IMF which represents different frequency components contained in the dynamic response.The other is the residue which represents the trend of the dynamic response.The Prony method is applied to identify the features of each component.Frequency similarity,amplitude similarity,damping similarity and phase similarity are defned based on these features.Based on the improved entropy weight[28],these feature similarities are composited into component similarity.Then quantitative validation metrics are obtained based on the energy proportion of components.According to the physical meaning of these features and the EMMD result,precise model error location can be realized when the validation metrics are undesirable.
2.Prony method based on EMMD
Prony method based on EMMD contains two steps.Firstly, complex dynamic responses are processed into stationary components by EMMD.Secondly,features of each component are identifed by the Prony method.
2.1EMMD
Integral mean value theorem(IMVT)is the theory foundation of EMMD.Suppose x(t)is a dynamic response.Its extrema are x(t1),x(t2),...,x(tq).Local means of every extreme point can be obtained through steps as follows.
Step 1Calculate mean values between all adjacent extreme points by IMVT.
The mean value between extreme points tiand ti+1is obtained by
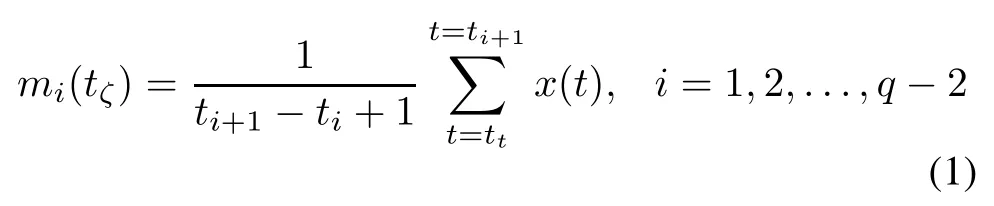
where tiis the location of the ith extreme point.Because the signal usually changes uniformly between adjacent extreme points,the mean value is located in the midpoint of adjacent extreme points.Then we can obtain the location tζby a formula as follows:

Similarly,the mean value between ti+1and ti+2can be described as

Step 2Calculate the local mean at every extreme point. The local mean at ti+1can be described as follows:
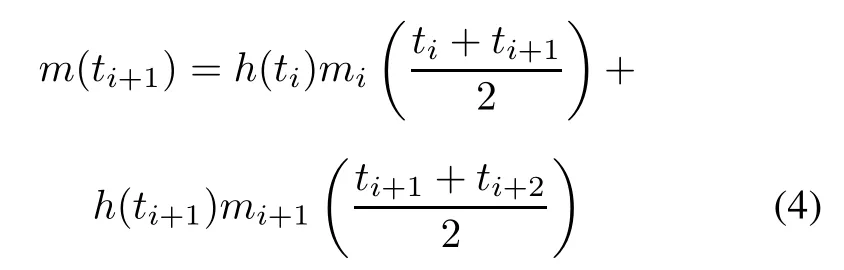
where

Local means of all extreme points can be obtained by repeating(1)–(5).Similar as EMD,EMMD also decomposes complex signal into the IMF and the residual.Suppose x(t)is a complex time series.Its EMMD result can be obtained as follows:
(i)Initialize gk(t)=x(t),k=1.
(ii)Find out all extrema of original signal gk(t)and calculate the local means at every extreme point by IMVT.
(iii)Obtain mean curve m(t)by applying cubic spline interpolation to the local means.The error between gk(t) and m(t)can be described as follows:
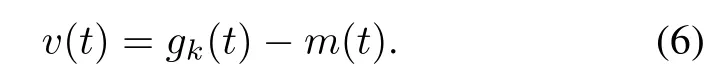
(iv)Judge v(t)is an IMF or not according to the formula as follows:
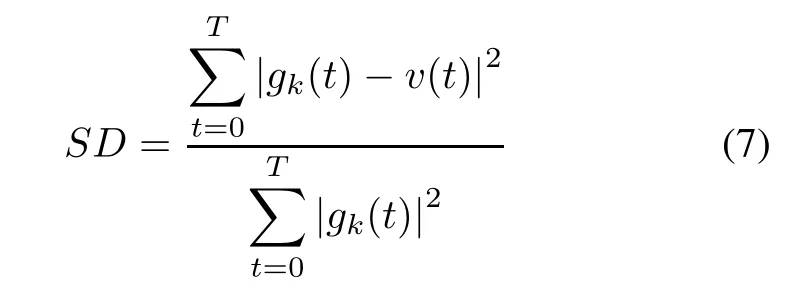
where T is the number of time series data points.SD is always set to le-3.If SD<le-3,v(t)is an IMF.Otherwise, v(t)is not an IMF.
(v)If v(t)is an IMF,ck(t)=v(t)and go to(vi).Otherwise,take v(t)as gk(t)and repeat(ii)to(iv)until v(t)is an IMF.
(vi)Remove ck(t)from x(t),the residual can be described as
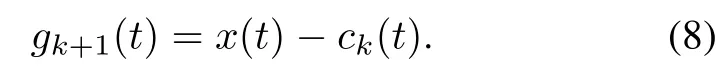
If the number of the extremum points ofgk+1(t)is more than two,take gk+1(t)as a new original signal and obtain its IMF by repeating(ii)–(v).If the number of the extremum points of gk+1(t)is less than two after repeating(ii)–(vi)L times,the decomposition can be stopped and the residual component of x(t)can be defned as r(t)=gL(t).
Finally,x(t)can be described by the formula as follows:

where ck(t)is the IMF which refects the character scale of the dynamic response.r(t)is the residual component which represents the trend of the dynamic response.In this paper,we call the IMF and the residual as EMMD components.
Because of the noise factor,IMF components usually contain some illusive components.They will affect the correctness of the validation result.Considering real IMF components are orthogonal to the original signal,they correlate with the original signal strongly.And illusive components correlate with the original signal weakly.Therefore,illusive components can be fltered by setting a restriction to the correlation coeffcient.Suppose ηi(i= 1,2,...,L)is the correlation coeffcient of the IMF and the original signal,the restriction can be defned as follows:
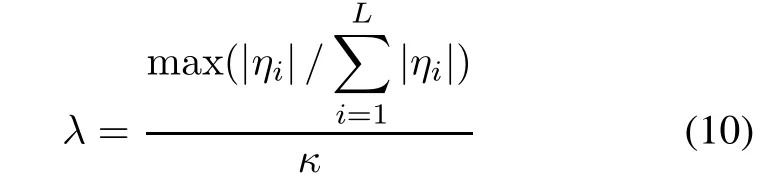
where κ is the proportionality which is suggested as 10 [29].If the correlation coeffcient of some IMF is smaller than λ,the IMF is an illusive component.It should be ignored in dynamic validation.
The real IMF and residual can refect the intrinsic character of a signal.We can analyze model error qualitatively by comparing EMMD components of the two signals.According to the physical meaning of the EMMD components,model error location can be realized roughly.However,if we want to know the error location precisely and assess model error quantitatively,other information about the features of the EMMD components is needed.In this paper,the Prony method is applied to identify the features of the EMMD components.
2.2Prony method
Prony method denotes a series uniformly simple data as linear combination of exponential functions (EFs).These EFs always have discretional amplitude, phase,frequency,and damping.Suppose time serie (x(0),x(1),...,x(n),...,x(N−1))is an EMMD component.In the Prony method,its estimate can be defned as follows:
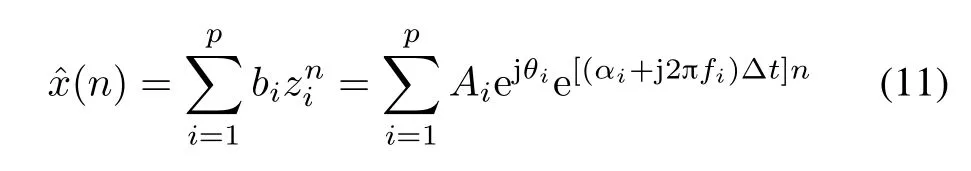
where Ai,fi,αiand θiare amplitude,frequency,damping and phase of the ith exponential function.Δt is the sampling period.p is the model order.It can be gotten by singular value decomposition(SVD)[20].
In the Prony method,ˆx(n)is ftted as the homogeneous solution of linear difference equations with constant coeffcient.It can be described by the formula as follows:

where αiis a constant.They can be obtained by solving (12).Its characteristic polynomial can be obtained by solving the formula as follows:
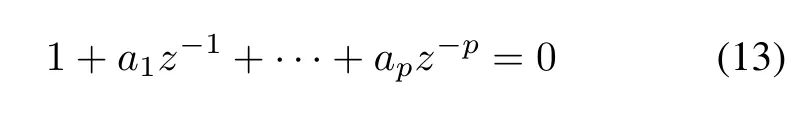
where ziis an eigenvalue.Then bican be obtained by solving the formula as follows:

Finally,Ai,fi,αiand θican be obtained by

These features are all quantitative.It is easy to obtain a quantitative assessment about the similarity of two signals by quantify errors on these features.Furthermore,these features always have clear physical meanings.For example,the amplitude refects the energy contained in a signal; the frequency refects the vibration character of a signal; the damping refects the station of a signal and the phase is the initial station of the signal.The physical meaning of these features makes precise model error location wellgrounded.
3.Dynamic validation based on EMMD and Prony method
3.1Data pretreatment
Suppose x(t)is the dynamic response of a model and y(t) is the dynamic response of the real system.Their EMMD results are described as follows:

where superscript x and y denote the signal x(t)and y(t). Subscript k denotes the kth IMF.rx(t)is the residual component of x(t)and ry(t)is the residual component of y(t).It is common that Lx/=Ly.In order to compare them with each other,dimensions of their IMF must be the same to each other.IMF of two similar signals always has the same energy order.Therefore,we take the energy proportion as the criterion to unify the IMF dimensions.Firstly,IMF of each signal is sorted according to their energy proportion from big to small.Secondly,a uniform dimension can be obtained by L=min(Lx,Ly).If L=max(Lx,Ly),the rest components of the signal with less dimension,for example Lx<Ly,should be 0,that is cxk(t)=0(k=Lx+1,...,Ly).Apparently,these components have no similarity with cyk(t)(k=Lx+1,...,Ly). It has no signifcance to make comparison between them and even produces weak infuence on the validation result.And redundant components are ignored.Finally,the EMMD results of the two signals can be described as follows:

When the IMF dimension is unifed,the Prony method can be applied to each EMMD component.The model order of each EMMD component also can be unifed in the same way as IMF.The dynamic response processed by EMMD and the Prony method can be described as follows:

where pkis the model order of the kth EMMD component.Subscripts m and r mean the features coming from the model or the real system.The subscript i denotes the ith exponential function.
3.2Feature similarity
If the model is valid,x(t)should be consistent with y(t) on these features,such as amplitude,phase,frequency and damping.In order to provide an intuitionistic validation result,we apply similarity to measure the feature error.Suppose the kth(k=1,2,...,L+1)EMMD component is the linear combination of exponential functions whose model order is pk,the frequency similarity on the ith(i=1,2,...,pk)exponential function can be denoted by the formula as follows:

where i=1,2,...,pk;k=1,2,...,L+1.fkmiand fkriare the frequency of ith exponential functions of the model and the real system respectively.ekfiis the threshold of the frequency error.Skfi=1 means the exponential functions are the same on frequency.And Skfi=0 means the frequency error of these two exponential functions is too big to accept.Similar to frequency similarity,we can also defne amplitude similarity,phase similarity,and damping similarity in the same way.
The threshold not only has great impact on the feature similarity value,but also has defnitely physical meanings. It can be obtained in two ways.One is to set it to a constant value;the other is to set it to a value changing along with the input data dynamically.Obviously,the second method fts the engineering practice better.We take the second method in this paper and make it change with the features of the real system response.
第一,融入创意旅游思维,开发新业态类型产品。挖掘乡村旅游地历史文化、民俗文化、民族文化、农业文化,并进行提炼、解析和延伸,[3]创造性转化这些文化,去深度创意乡村旅游产品,拓展与开发原乡休闲、国家农业公园、乡村营地、乡村庄园、休闲农场、乡村博物馆、市民农园、民宿等新业态产品,使旅游者在享受乡村田园风光的同时,获得发掘创造潜能的机会,学习并体验乡村旅游地文化、艺术、传统及生活方式,实现乡村旅游由农家乐、采摘园向乡村休闲度假的跨越。
After getting all the feature similarities by(19),the feature similarities of the kth(k=1,2,...,L+1)EMMD component can be described by matrix SFkas follows:

Merge the feature similarities by column,comprehensive feature similarity of the kth EMMD component can be described by matrixas follows:

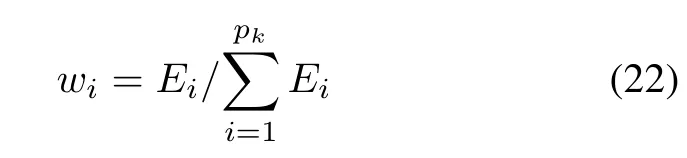
where Eiis the energy of the ith exponential function.Finally,the comprehensive feature similarity of all EMMD components can be denoted by a matrix as follows:
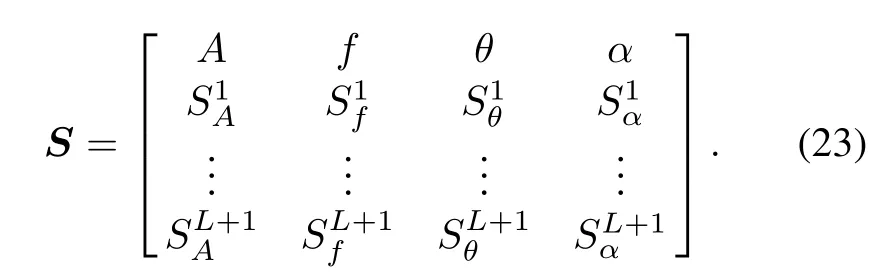
Commonly,it can also be rewritten as
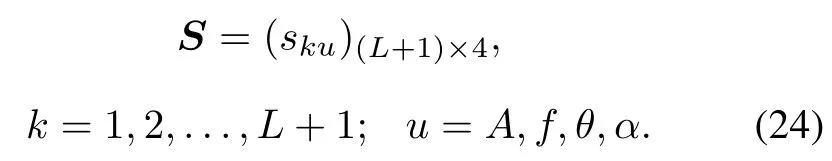
This matrix shows the comprehensive feature similarities of all EMMD components.By compositing skuin row,we can get the comprehensive similarity of each EMMD component.In order to minimize the infuence of subjective factors,we composite skuaccording to the information entropy weight of each feature and obtain validation metrics by compositing component similarities according to their energy proportions.
3.3Improved entropy weight
Information entropy weight is widely used as an index weight in comprehensive evaluation.The information entropy weight of a feature is decided according to the information that can be transferred to users by the feature.The bigger the difference of feature similarities is,the more information the feature can transfer.And it is more important of the feature in similarity composition.The information entropy weight of features can be obtained by steps as follows.
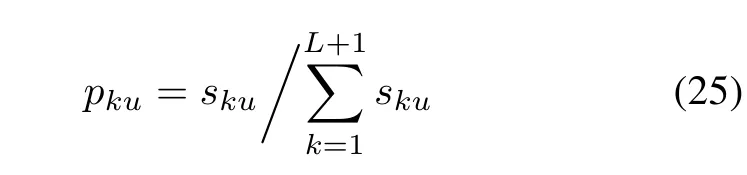
Step 2Calculate the information entropy by the formula as follows:
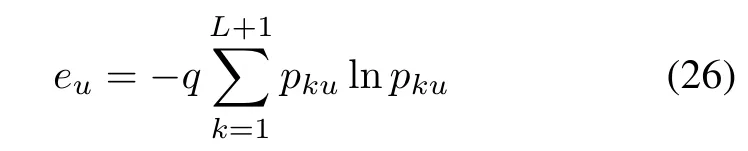
where q=1/ln(L+1),0≤eu≤1.
Step 3In the original information entropy,the entropy weight can be obtained by the formula as follows:
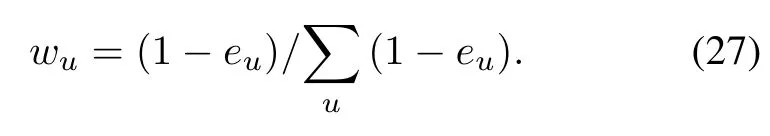
In this formula,a small difference between eumay leads to a big difference change in the entropy weight when eu→1.For example,an information entropy set is [0.998,0.997,0.996,0.993],and their entropy weight set is [0.125,0.1875,0.25,0.4375].Obviously,this result is unreasonable.According to the information entropy theorem, if difference between the information entropy of each feature is as small as possible,each feature of the information can supply is the same with each other.And their entropy weight should also be similar to each other.Therefore,the improved entropy weight can be obtained by the formula as follows:
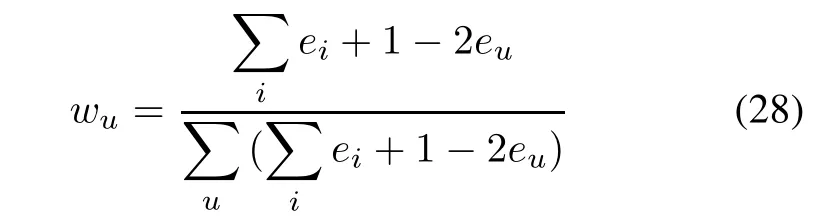
The information entropy is the measurement of system uncertainty.The improved entropy weight can not only avoid subjective factors brought by suggestions form experts,but also ft engineer practice better than the original entropy weight.According to the information entropy weight of each feature,component similarity of the kth EMMD component can be obtained by the formula as follows:?

And component similarity can be described by
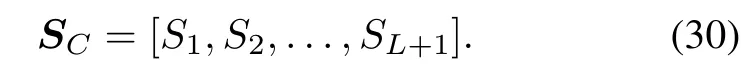
3.4Validation metrics
To composite component similarity into validation metrics objectively,the weight of the kth(k=1,2,...,L+1) EMMD component is decided by its energy proportion in dynamic response y(t).It can be obtained by the formula as follows:
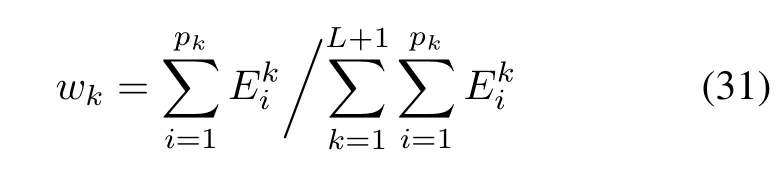
where Ekiis the energy of the ith exponential function in the kth EMMD component.Based on the weight of EMMD components,dynamic response similarity can be obtained by the formula as follows:
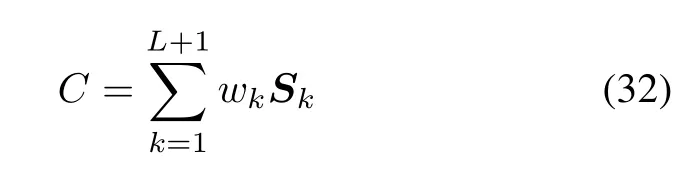
where C=1 means the model is consistent with real system.Their dynamic responses have the same features. C=0 means feature errors between dynamic responses are unacceptable and the model is not credible.And if C∈(0,1),it means the model is applicable and the user should take some risks.Therefore,it is common that C is too small to be accepted by users.To improve C to satisfy the requirement,a model updating plan should be made to improve the credibility of the model.The method proposed in this paper can provide enough information for the plan making.
3.5Model updating based on validation process
Fig.1 is the process of locating model errors based on the model validation process.Ciis an intended credibility criterion.In this process,model error location can be realized by two steps.Firstly,locate model errors in the subsystem. Secondly,fnd the error parameters in the subsystem.

Fig.1 Process of model updating
In Fig.1,we locate model errors in some subsystems according to the component similarity by(30)when a model is not credible enough to its application.That is to say the components with little similarity are the sources of model errors.The physical meaning of the EMMD components provides effciency guidance for us to locate model errors in its subsystem.In EMMD components,the IMF always reveals the frequency character of a dynamic response and the residual always reveals the trend of a dynamic response.For example,if the S1in(30)is too small, that means the high frequency part in the model needs to be modifed.
A subsystem may contain many modules and have many parameters.Just locating model errors in the subsystem can not modify the model effectively.According to(23), we can locate model errors on the features that have small similarity.These features always have clear physical meanings.We can locate model errors on the parameters of the subsystem.If the relationship between parameters and features is not clear enough,sensitivity analysis can be applied to decide the key parameters of the feature.Different from the common sensitivity analysis process,we just need to run the subsystem instead of the whole system.This cansave a lot of computer time and improve the model updating effciency.When we locate model errors on these parameters,we can update the model conveniently.
4.Case studies
Controller design is a key issue of the hypersonic vehicle research feld.Control-oriented modeling is an important and fundamental step in controller design[30,31].In order to design the controller conveniently,a high resolution model(HRM)or principle model always needs to be simplifed to a control-oriented simple model(SM)according to some assumptions,such as linearity and fexibility ignorance.It is an important and challenging process for model developers and controller designers to develop an SM.If SM is not credible enough,it is meaningless to design controller for it.Furthermore,more serious accidents would be brought about when a controller designed based on a wrong model is applied to a real system.In order to design the controller precisely,the SM must be validated and enough evidence must be collected about its credibility.
The angle of attack is an important dynamic performance indicator of hypersonic vehicles.It reveals the motor performance of the hypersonic vehicle.If an SM is available,its angle of attack should have similar characters with HRM.In this case,we validate the angle of attack coming from HRM and SM of some hypersonic vehicles and locate model errors to provide information to update SM.Fig.2 is the angle of attack from HRM and SM in controller design for hypersonic vehicles.The sampling period is 0.01 s and the total sample time is 40 s.The solid line is the angle of attack from HRM and the dashed line is the angle of attack from SM.We can see that these two data series are unstable and nonlinear.They are similar to each other on trend and vibration characteristics.In order to measure their similarity quantitatively and locate model errors precisely,we apply the method proposed in this paper to validate the SM.
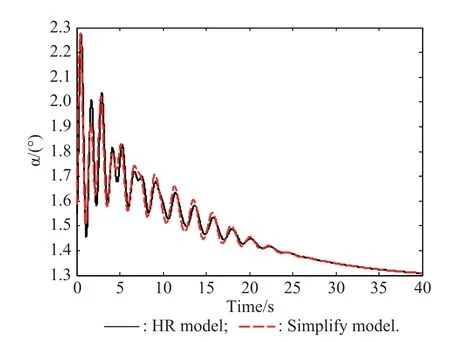
Fig.2 Comparison of angle of attacks from HRM and SM
Following the process of this method,we decompose the dynamic responses into the IMF and the residual by EMMD and flter noise components frstly.Fig.3 is the real EMMD components of each signal.The third subgraph of each signal is their residual components.
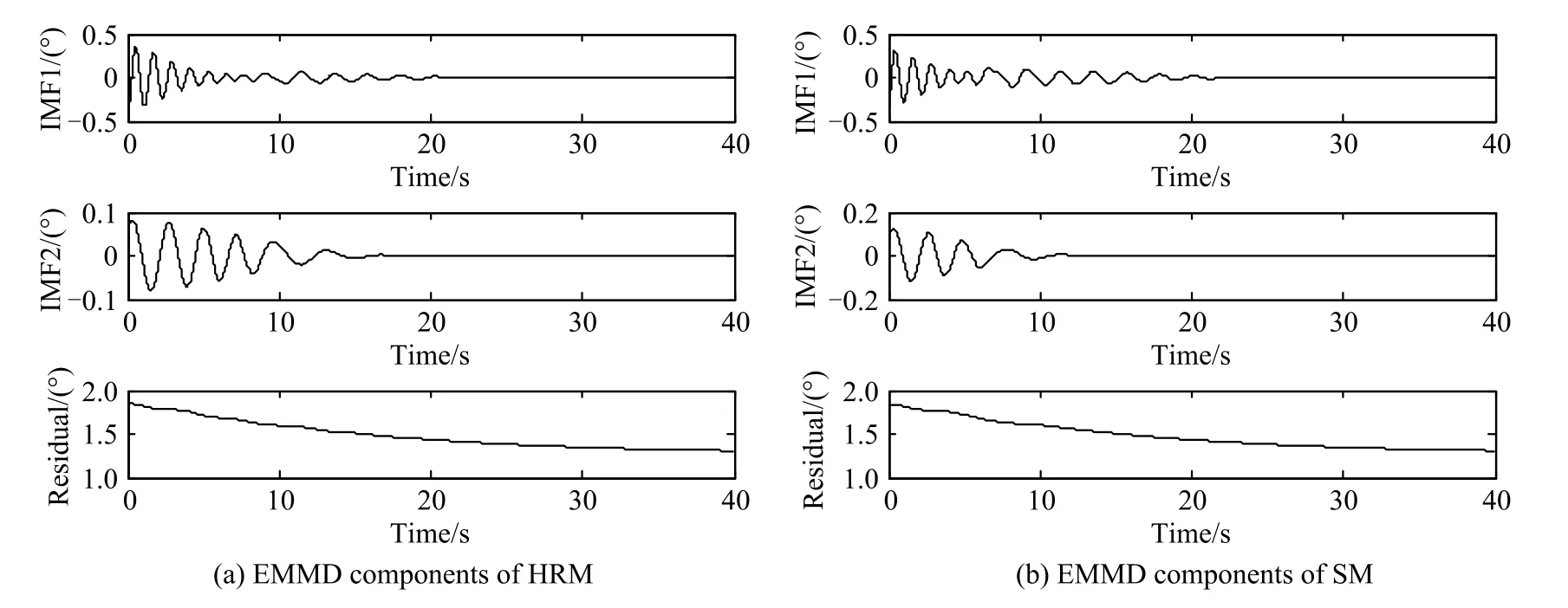
Fig.3 EMMD components of each signal
Fig.3 shows that EMMD components of the two signals are similar to each other.Although it gives us an intuitionistic opinion about the similarity of EMMD components,it cannot provide us with quantitative information about component similarities or distinct error information. By applying the Prony method to every component,we can obtain their features.Table 1 is the exponential function parameters of each EMMD component.

Table 1 Exponential function of each EMMD component
According to(22),we can obtain weights of exponential functions by the energy proportion.Table 2 is the weight of each exponential function.

Table 2 Weight of each exponential function
We can see that the energy of the exponential function is concentrated.That means the EMMD result is correct.If a rough estimation is required,we can ignore these exponential functions whose energy proportion is small.In order to prevent information losing,we take all these functions into consideration.Taking 30%feature value of HRM as a threshold,their comprehensive feature similarity can be computed by(19)–(24).The comprehensive feature similarities are denoted by the matrix as follows.

This result shows that IMF1 of two dynamic responses is similar to each other on frequency and phase features, but different on damping and amplitude.IMF2 is similar to each other on frequency and damping features,but different on amplitude and phase.Their residuals are similar to each other on every feature.This result is consistent with Fig.3.
According to(25)–(28),the improved entropy weight of each feature can be denoted by

This result reveals that the amplitude is the most important feature.Phase and damping are second important features.This result is consistent with feature similarity matrix S.According to(29)and(30),component similarities can be denoted as follows:
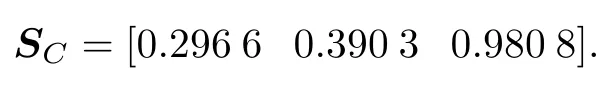
This result shows that two dynamic responses have good consistency on residuals,but bad consistency on their trend components.This result is also consistent with Fig.2 and Fig.3.
According to(31),the weight of each EMMD component is denoted as follows:

This result shows that the frst EMMD component has a decisive impact on response similarity.According to(32), the validation metric is
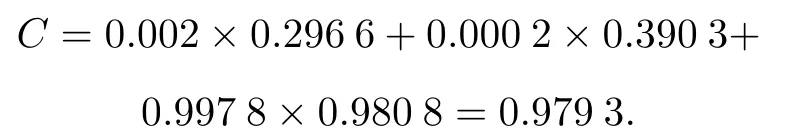
It means the SM is consistent with HRM greatly.Compared with TIC(0.011 1,the smaller the better)and grey relational analysis(0.968 5,the bigger the better)method, this metric is not only consistent well with them,but also quantitative and objective.Different from these two methods,the validation metrics are calculated under a specifc threshold.If the model user can undergo a bigger error,this result can reveal this condition by changing the threshold. What is more important is that the progress of this method can provide more information about model errors.If the user is not satisfed with the metrics,this method gives us enough information to improve the model.Following the process shown in Fig.1,we locate model errors on its high frequency partition or model by SC.According to the control system design theory,the model error can locate on partition with a high order transfer function.According to S,IMF1 has a bad similarity on damping and amplitude. Thus,errors in SM can be located on these parameters that have great infuence on damping and amplitude.
5.Conclusions
Credibility is the lifeline of a model.How to improve the low credibility model to make it available is a key problem faced by model validation.It means the validation method not only provide information to decide a model is available or not,but also provide information to guide model updating.In this paper,a model updating-oriented dynamicvalidation method based on EMMD-Prony method is proposed.The complex dynamic series are decomposed into IMF and residual components by EMMD.These components always have clear physical meanings which can provide evidence about locating model errors roughly.The Prony method,which is applied to EMMD components to identify their physical features,can make consideration on damping which is always ignored by the existing method. The Prony method based on EMMD overcomes the drawbacks in the unstable and noisy signal process.It makes the Prony method more practical.The application of the improved entropy weight and the energy proportion makes validation metrics more objective.The quantitative validation metrics provide intuitionistic evidence about model credibility.Because all these features and EMMD components have specifc physical meanings,they can provide evidence about model error location and guide model updating.
In comparison with traditional methods,such as TIC and grey relational analysis,the proposed method can not only get the quantitative metrics,but also reveal more information about the dynamic response which can be the evidence about precise model error location.Model credibility growth would be realized by changing values of these parameters that have great infuence on these features.Furthermore,its result can change with the threshold that makes it conform to the engineer practice better.
In comparison with EARTH series methods,the proposed method not only takes consideration of features that refect the response wave form,but also of damping and frequency.It is a comprehensive analysis of the dynamic response.More important is that this method does not need suggestions from experts in the calculation of validation metrics.Its result is more objective than EARTH.Furthermore,the method also does not need to take consideration of feature relativity and warping data.It can make full use of information contained in the signal and calculation effciency.Given the features and EMMD components always have defnite physical meanings,the proposed method can not only provide quantitative evidence about the model credibility,but also guide the model updating effectively.
This method has great signifcance to model validation and model updating for dynamic systems with nonlinear and nonstationary time series response.It can expand the research feld of model validation and model updating,and has great signifcance to model credibility growth.
[1]B.Osman.A life cycle for modeling and simulation.Simulation,2012,88(7):870–883.
[2]ASME.Guide for verifcation and validation in computational solid mechanics.American Society of Mechanical Engineers: ASME Standard V&V 10-2006,2006.
[3]Y.Xiong,W.Chen,K.L.Tsui.A better understanding of model updating strategies in validating engineering models. Computer Methods in Applied Mechanics and Engineering, 2009,198:1327–1337.
[4]J.F.Ding,Z.Y.Han,X.R.Ma.Research evolution on the test verifcation of spacecraft dynamic model.Advances in Mechanics,2012,42(4):395–405.
[5]Z.Zhan,Y.Fu,R.J.Yang,et al.An enhanced bayesian based model validation method for dynamic systems.Journal of Mechanical Design,2011,133(4):41–45.
[6]X.M.Jiang,M.Sankaran.Bayesian risk-based decision method for model validation under uncertainty.Reliability Engineering and System Safety,2007,92:707–718.
[7]N.A.Kheir,W.M.Holmes.On validating simulation models of missile systems.Simulation,1978,30(4):117–128.
[8]J.Wu,X.Y.Wu,Y.X.Chen,et al.Validation of simulation models based on improved grey relational analysis.Systems Engineering and Electronics,2010,32(8):1677–1679.(in Chinese)
[9]S.Jiao,W.Li,M.Yang.Validation of simulation models based on empirical modal decomposition and grey relevance analysis.Systems Engineering and Electronics,2013,35(12): 2613–2618.(in Chinese)
[10]L.You,M.D.Sankaran.Quantitative model validation techniques:new insights.Reliability Engineering and System Safety,2013,111:217–231.
[11]W.Oberkampf,M.Barone.Measures of agreement between computation and experiment:validation metrics.Journal of Computational Physics,2006,217(1):5–36.
[12]X.M.Jiang,S.Mahadevan.Wavelet spectrum analysis approach to model validation of dynamic systems.Mechanical Systems and Signal Processing,2011,25:575–590.
[13]F.M.Hemez,S.W.Doebling.Validation of structural dynamics models at Los Alamos National Laboratory.Proc.of the 41st AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference,2000.
[14]L.E.Schwer.Validation metrics for response histories:perspectives and case studies.Engineering with Computers,2007, 23:295–309.
[15]C.J.Kat,P.S.Els.Validation metric based on relative error.Mathematical and Computer Modelling of Dynamical Systems,2012,18(5):487–520.
[16]T.L.Geers.An objective error measure for the comparison of calculated and measured transient response histories.Shock and Vibration Bulletin,1984,54:99–107.
[17]D.M.Russell.Error measures for comparing transient data–Part I:development of a comprehensive error measure.Proc. of the 68th Shock and Vibration Symposium,1997:175–184.
[18]H.Sarin,M.Kokkolaras,G.Hulbert,et al.A comprehensive metric for comparing time histories in validation of simulation models with emphasis on vehicle safety applications.Proc.of the ASME International Design Engineering Technical Conference and Computers and Information in Engineering Conference,2008.
[19]Z.F.Zhan,Y.Fu,R.J.Yang.Enhanced error assessment of response time histories(EEARTH)metric and calibration process.Proc of the SAE World Congress,2011.
[20]X.D.Zhang.Modern signal processing.Beijing:TsinghuaUniversity Press,2002.(in Chinese)
[21]S.L.James,W.L.Yang,H.J.Li.Signal decomposition and reconstruction using complex exponential models.Mechanical Systems and Signal Processing,2013,40:421–438.
[22]S.Gao,R.M.He,J.Ma,et al.Error criteria on power system dynamic simulation validation.Automation of Electric Power Systems,2006,30(4):6–10.(in Chinese)
[23]W.B.Hou,T.Q.Liu,X.Y.Li.Prony analysis of low frequency oscillations based on empirical mode decomposition fltering. Acta Physica Sinica,2010,59(5):3531–3537.(in Chinese)
[24]X.Y.Li,R.K.Zhu,Y.H.Wang.Parameter identifcation of synchronous machine based on empirical mode decomposition and prony algorithm.Power System Technology,2012,36(8): 136–139.(in Chinese)
[25]Z.He,Y.Shen,Q.Wang,et al.Mitigating end effects of EMD using non-equidistance grey model.Journal of Systems Engineering and Electronics,2012,23(4):603–611.
[26]Q.Gai.Research and application on the theory of loeal wave time-frequency analysis method.Dalian:Dalian University of Technology,2001.(in Chinese)
[27]Z.M.Lu,M.L.Sun,C.X.Zhang,et al.Speech enhancement method based on extremum feld mean mode decomposition.Systems Engineering and Electronics,2011,33(7): 1680–1684.(in Chinese)
[28]B.D.Hou,J.L.Li,N.Pan,et al.Application of grey relevancy model based on ameliorated entropy for comprehensive evaluation of wetland environment quality.Journal of Safety and Environment,2008,8(6):80–83.(in Chinese)
[29]Q.Liu,Z.P.Wang,Y.Zhang.A novel method of transient protection for shunt compensated lines based on hht spectrum analysis.Transactions of China Electrotechnical Society, 2011,26(11):201–209.
[30]H.F.Li,P.Lin,D.J.Xu.Control-oriented modeling for airbreathing hypersonic vehicle using parameterized confguration approach.Chinese Journal of Aeronautics,2011,24:81–89.
[31]M.D.Firoozabadi,M.Shahbakhti,C.R.Koch.Thermo dynamic control-oriented modeling of cycle-to-cycle exhaust gas temperature in an HCCI engine.Applied Energy,2013,110: 236–243.
Biographies

Yongxing Chen was born in 1987.He received his B.S.and M.S.degrees from the Missile Institute,Air Force Engineering University in 2008 and 2011,respectively.He is currently working towards his Ph.D.degree in Air and Missile Defense College,Air Force Engineering University. His current research interests include system modeling and simulation,VV&A and model credibility assessment.
E-mail:yongx c@163.com

Xiaoyan Wu was born in 1957.She received her B.S.degree in automatic control from Shaanxi Mechanism College in 1982 and M.S.degree in navigation guidance and control from Air Force Missile Institute in 1993.She is currently a Ph.D.and professor in Air and Missile Defense College,Air Force Engineering University.Her main research interests include fight vehicle modeling,simulation, VV&A,model credibility assessment and control theory and application.
E-mail:x ywu@126.com

Xiangwei Bu was born in1987.He received his B.S. and M.S.degrees from Air and Missile Defense College,Air Force Engineering University in 2010 and 2013,respectively.He is currently a Ph.D.candidate in Air and Missile Defense College,Air Force Engineering University.His research interests mainly lies in hypersonic vehicle modeling and control.
E-mail:buxiangwei1987@126.com

Ruiyang Bai was born in 1991.He received his B.S. degree from Nanjing University of Aeronautics and Astronautics in 2012.He is currently an M.S.candidate in Air and Missile Defense College,Air Force Engineering University.His current research interests include fight vehicle modeling,simulation,and VV&A.
E-mail:brynuaa@163.com
10.1109/JSEE.2015.00022
Manuscript received March 24,2014.
*Corresponding author.
This work was supported by the Nature Science Foundation of Shaanxi Province(2012JM8020).
 Journal of Systems Engineering and Electronics2015年1期
Journal of Systems Engineering and Electronics2015年1期
- Journal of Systems Engineering and Electronics的其它文章
- Dynamic channel reservation scheme based on priorities in LEO satellite systems
- Adaptive beamforming and phase bias compensation for GNSS receiver
- Novel dual-band antenna for multi-mode GNSS applications
- Nonparametric TOA estimators for low-resolution IR-UWB digital receiver
- Effcient hybrid method for time reversal superresolution imaging
- Adaptive detection in the presence of signal mismatch
