纸浆悬浮液纤维模型的研究进展

高致富 张 锋 王三刚

(1.陕西科技大学轻工与能源学院, 陕西西安, 710021；2.陕西省造纸技术及特种纸开发重点实验室, 陕西西安, 710021)



·纸浆悬浮液纤维模型·

纸浆悬浮液纤维模型的研究进展

高致富1,2张 锋1,2王三刚1

(1.陕西科技大学轻工与能源学院, 陕西西安, 710021；2.陕西省造纸技术及特种纸开发重点实验室, 陕西西安, 710021)

纤维模型对于应用计算机仿真技术模拟纸浆悬浮液中纤维运动特性是非常必要的。目前国内外对纤维模型的建模方式有刚性纤维模型和柔性纤维模型。笔者概述了国内外纤维模型的发展情况,着重分析了刚性纤维模型和柔性纤维模型的建模思想,通过对比分析各种纤维模型的适用范围、优越性和局限性,提出了纤维模型的发展趋势。

纸浆悬浮液；纤维；模型；仿真；流体

(*E-mail： 710140884@qq.com)

随着计算机技术的发展,计算机辅助工程(CAE)已经成为现代机械产品研发的主要手段,而制浆造纸设备的研发也不例外。为了得到更好的纸机成形设备,需要真实地仿真分析纤维悬浮液在纸机成形设备中的流动情况。因而,建立纸浆悬浮液的纤维模型对于纸机成形设备的发展显得尤为重要。然而,纸浆纤维是一种细长柔软具有可塑性的固相物质,其在纸浆流动过程中不是简单的随流体流动方向而运动,而是同时具有弯曲、扭转、翻滚等多种复杂的运动形式。根据纤维模型是否具有可变形性,将纤维模型分为刚性纤维模型和柔性纤维模型。目前国内对纸浆纤维与悬浮液之间的作用机理研究虽取得一些成果,但仍有许多问题未得到合理解释,在一定程度上限制了纤维悬浮液流动过程中纤维取向分布及其流动特性的有效控制,致使国内纸浆纤维模型的研究主要集中于刚性纤维模型。然而,柔性纤维模型更接近于纤维的真实情况，可以更灵活具体地反映纤维在流体中的变形,使纤维的流体动力特性计算更接近于实际情况。因此,研究和理解纤维悬浮液中纤维与流场间潜在的作用机理,建立合理的物理模型对于纸机成形设备的开发具有十分重要的理论和实际意义。笔者在对刚性纤维模型分析基础之上,主要针对不同柔性纤维模型的建立理论进行阐述和对比分析。

1 刚性纤维模型

1922年,Jerrery[1]首先研究了椭球粒子在简单剪切流中的运动,发现粒子在一个闭合椭圆轨道上做周期性旋转运动。1962年,Bretherton[2]的研究表明，任何一个轴对称刚体粒子在简单剪切流中运动时都有一个封闭固定不会漂移的轨道。Bretherton通过引入等效长径比概念,将Jerrery对椭球粒子的研究方法推广到任何轴对称粒子。假设轴对称粒子处于球坐标中,如图1所示,粒子对称轴方向的单位矢量可表示为(sinθcosφ,sinθsinφ,cosθ),则粒子的运动方程为：

图1 纤维粒子方位角示意图

(1)

(2)

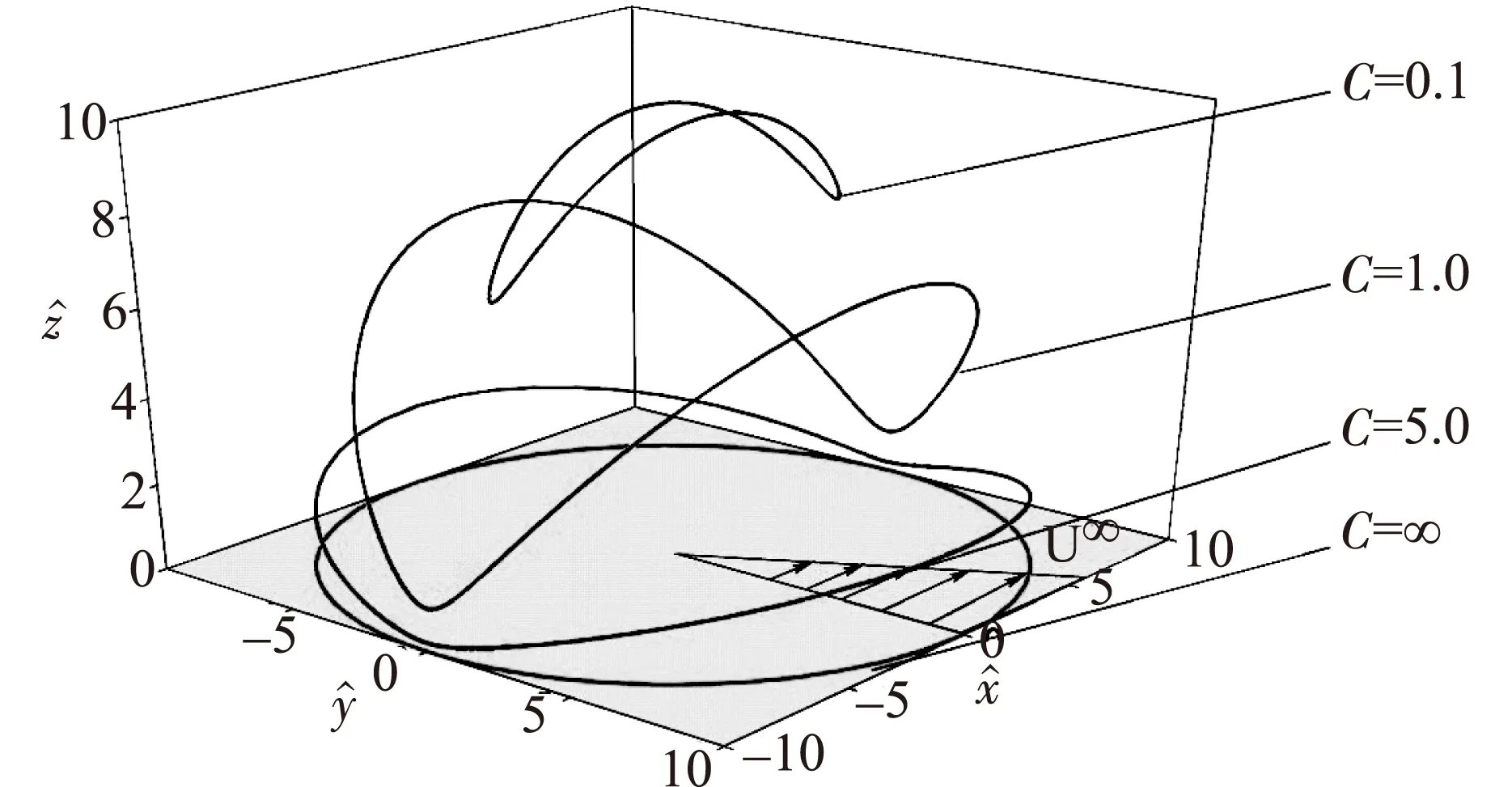
图2 在长径比rp=10时不同轨道常数下粒子轨道

近年来,国内研究者对纤维粒子运动研究一般采用刚性纤维模型,其中付平乐等人[3]提出了刚性球形纤维模型，研究发现在低浓度下,纤维在流动中所受的彻体力R、流体拖动力P、旋转升力F1等作用力与纤维悬浮液中所具有的形状以及形状的变化并无关系,而只与纤维打浆帚化后在悬浮液中所占有的空间外表面积的大小有直接关系。由此他引入球形纤维粒子的假设,把细长柔软可塑性的固态纤维,看作一个外表面积相同而形状不发生改变的球形纤维粒子,如图3所示。整个纤维悬浮液是由液态水和固态球形纤维粒子共同组成,球形粒子与液态水的作用力等效于固态纤维与水的作用力,而球形粒子的运动即可表示纤维粒子在悬浮液中的运动。肖宗亮[4]对纤维模型进行推广,采用等面积法和等体积法对刚性椭球和圆柱形纤维粒子进行了研究。

图3 纤维外表面积模拟的球体模型

国内采用上述刚性纤维模型的实验研究结果表明,刚性纤维模型的运动特性与Jerrery理论相符合。因此可采用Jerrery的研究方法对刚性纤维模型在流场中的运动情况进行模拟。然而,研究表明随着纤维浓度的增加,纤维变形或纤维与纤维之间的相互作用对纸浆悬浮液的动力学特性影响更加突出,已不可忽略。由于刚性纤维模型并没有考虑纤维之间的相互作用,因此刚性纤维模型只适用于低浓度、底剪切作用下的纤维悬浮液。为了弥补刚性纤维模型的不足,国内外学者相继提出了柔性纤维模型。

2 柔性纤维模型

刚性纤维模型是把纤维当作刚性粒子,忽略了纤维在流体运动中的变形。为了进一步认识清楚纤维粒子在流体中的运动情况,Yamamoto等人[5]首先提出了柔性纤维模型,后来其他学者在其模型基础上继承并发展。目前,主要柔性纤维模型有圆球形纤维模型、椭球链纤维模型和圆柱杆链纤维模型。

2.1 圆球形纤维模型

根据圆球间的连接方式不同,可将圆球形纤维模型分为Yamamoto圆球形纤维模型和Paal Skjetne圆球链纤维模型。

2.1.1 Yamamoto圆球形纤维模型

1993年,Yamamoto等人[5]提出了一种类似于模拟分子动力学的纤维模型,将圆柱杆纤维看作为一连串球体排列连接而成,其结构如图4所示。若单个纤维是由N个半径为a的球体排列构成,结构如图5所示,则圆柱杆纤维直径为2a、长度为2Na、长径比为N。相邻圆球体之间通过连接距离、弯曲角度和扭转角度将其约束在一起。该模型可以通过改变相邻球体之间的连接距离、弯曲角度以及扭转角度,模拟纤维在流体中产生拉伸、弯曲和扭转变形，其作用方式示意图见图6。

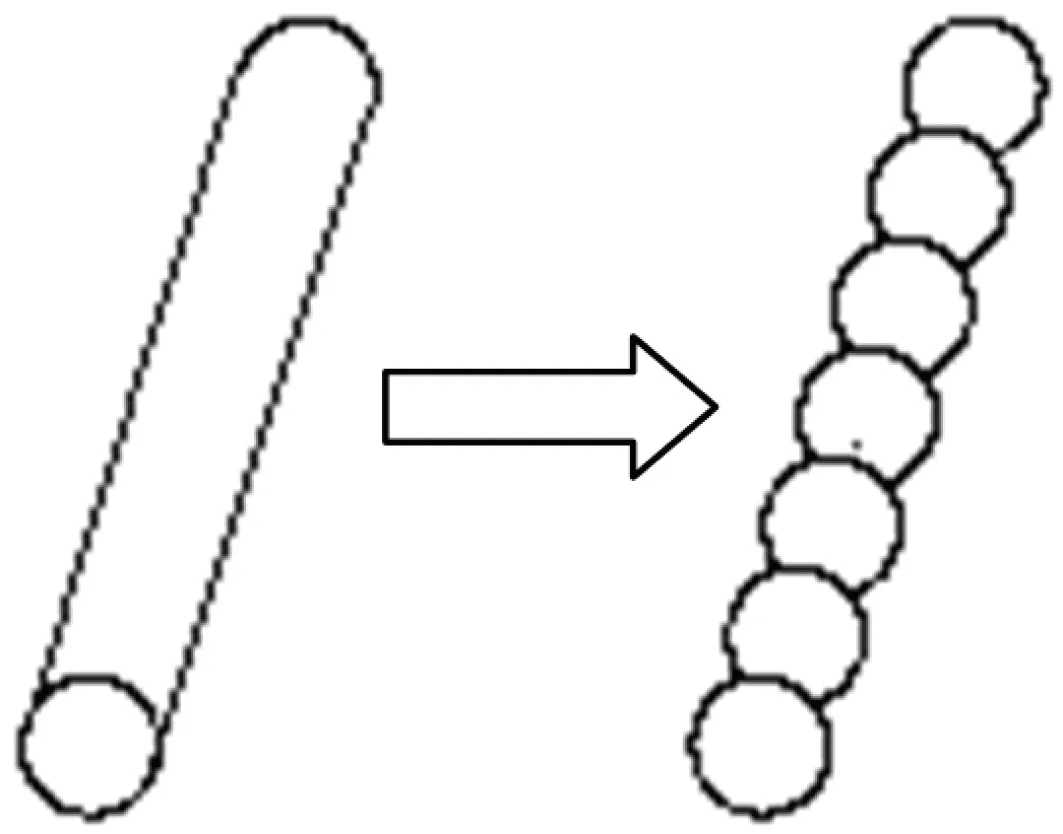
图4 单个纤维球体组成示意图

图5 由N个半径为a球体组成的纤维模型示意图

(1)纤维拉伸。图6(A)为纤维拉伸示意图,在平衡状态时,相邻两圆球体之间都有其平衡距离r0(r0=2a),若将相邻圆球体之间的距离拉伸到r时,作用在每个球上的拉伸力Fs为:

Fs=-ks(r-r0)

(3)

式中,ks是拉伸常数,与纤维特征和杨氏模量有关；r0是纤维平衡态的相邻两球连接距离。

(2)纤维弯曲。图6(B)为纤维弯曲示意图,使相邻两圆球的连接角度从θb0到θb的弯矩Tb为:

Tb=-kb(θb-θb0)

(4)

式中,kb是弯曲常数,与纤维特征与杨氏模量有关；θb0是纤维平衡态的弯曲角(θb0=0)。

(3)纤维扭转。图6(C)为纤维扭转示意图,相邻两圆球的扭转角度从平衡态θt0到θt的转矩Tt为:

Tt=-kt(θt-θt0)

(5)

式中,kt是扭转常数,与纤维特征与剪切模量有关；θt0是平衡时扭转角(通常θt0=0)。

图6 相邻圆球体之间的作用方式示意图

通过上述建模,可以模拟柔性纤维在流体中的运动状态。通过改变纤维模型的拉伸常数、弯曲常数和扭转常数,模拟不同柔软度的纤维粒子。当这些参数都相当大时,可以看作刚性纤维。通过分析求解纤维模型中每个球体在流体中所受的力和力矩,建立纤维粒子的平动和转动方程,从而可知纤维粒子在流体中的运动状态。

(6)

(7)

式中,m为球体质量；ri为球体i的位置；θi为球体i的角度；nij为相邻两圆球中心距离的单位矢量。

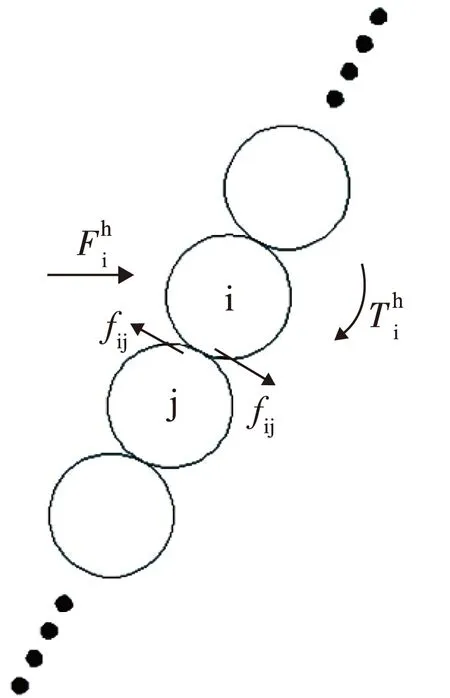
图7 圆球体i的受力分析

这种纤维模型的优势主要表现为：①可模拟任意形状的粒子,具有良好的适用性；②可模拟不同柔软度的纤维粒子；③模拟方法简单。该模型主要局限于低浓度和低雷诺数条件下，只考虑纤维间短程润滑力时的剪切悬浮流时纤维的运动变形情况；且此模拟方法的计算过程比较复杂,每一步都满足一组迭代约束方程,需要进行迭代运算,从而对计算机性能要求较高。

2.1.2PaalSkjetne圆球链纤维模型

PaalSkjetne圆球链纤维模型与Yamamoto圆球形纤维模型相似。然而,PaalSkjetne等人[6]建立的柔性纤维模型是采用球铰链连接的刚性球珠链,如图8所示。单个纤维模型由多个子单元纤维模型组成。子单元的圆球体一端连接无质量小球,另一端连接通过球质心的球窝,小球和球窝距球体表面距离分别是k1和k2；单个纤维模型中总共有N个球铰链。其中有N-1个球铰链由于使用球窝关节限制了相邻球珠之间的平动,所以这N-1个球铰链只有3个旋转自由度；但有一个球铰链连接到参考系中,因此这个球铰链有6个自由度,所以该纤维模型可以模拟真实纤维的平动和转动过程。

图8 纤维模型子单元的几何形状示意图

若球珠用希腊字母(ν,η,к,…=1,…N)表示,球铰链用拉丁字母(,b,c,…=1,…N)表示。定义整数函数i+(α)=-1,i-(α)=分别为球珠内侧和外侧,连接矩阵S和其逆矩阵T分别由式(8)、式(9)定义:

(8)

图11 椭球体和铰链编号示意图

(9)

显而易见,这两个矩阵有下列关系：

S·T=T·S=δ，δ为N·N列单位矩阵。

上述定义了球珠之间的连接方式,那么就可以通过求解圆球链纤维模型中单个球珠ν运动来模拟纤维在流场中的平动和转动。圆球链纤维模型中单个球珠受力有通过球珠质心的合外力Fν和球铰链b、c处的内部约束力Xb、Xc,这些力产生的力矩有合外力力矩Mν和约束力矩Yb、Yc,受力情况如图9所示。

图9 球珠ν受力示意图

纤维模型中每个球珠在流场中的运动都满足牛顿第二定律和角动量守恒定律。对球珠ν应用牛顿第二定律有：

(10)

对球珠ν由角动量平衡定律可得：

(11)

该纤维模型可以模拟纤维在无界线性剪切流和抛物线剪切流条件下运动变形情况。同时,该模型无需迭代约束来保持纤维之间的连接,因此这有助于减少计算机的运算量,提高计算机运行速度和计算效率。但是该模型在模拟过程中忽略了球珠惯性和球珠之间的水动力作用(与第一模型之间的三种变形的受力处理方式不同,导致模型迭代数量减少,降低对计算机的性能要求)。

2.2 椭球体链纤维模型

相比于Paal Skjetne等人模型,Ross等人[7]提出了球铰连接的椭球体链建立柔性纤维模型的新型模拟方法,如图10所示。a为长半轴,b为短半轴,参数是两椭球间距(一般ε=0.01b)。在纤维悬浮液中,每个柔性纤维由N个刚性椭球体通过N-1个小球和球铰关节所连接,各球铰关节有3个转动自由度,因此该模型可以模拟纤维在流场中的弯曲和扭转变形。在剪切流中纤维拉伸变形相当于其他变形来讲是很小的，所以经常被忽略。在球铰关节处定义约束称为阻力势,对于不同阻力势可以模拟不同柔性的纤维。

图10 柔性纤维刚性椭球体连接示意图

整数函数i+()和i-()与PaalSkjetne模型定义方式相同；则连接矩阵S和T为：

(12)

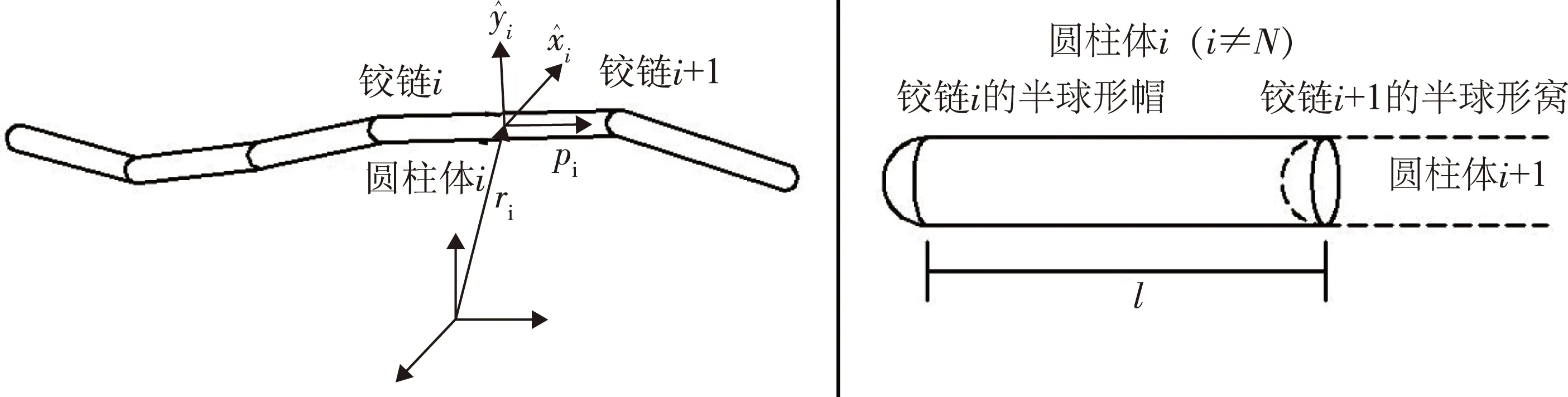
图13 圆柱杆链纤维模型示意图

(13)

同样这两个矩阵性质为：

TS=ST=E

E=N·N单位矩阵

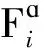
图12 椭球体i受力分析示意图

单个椭球体i用牛顿第二定律表示的动力学方程为：

(14)

单个椭球体i用角动量守恒定律表示为：

(15)

该模型不仅能够对单个纤维在流场中的运动进行准确预测与模拟,也能在实验过程中观察到因纤维变形而引起的运动轨道偏移现象[6],而且还可计算出纤维悬浮液的瞬态相对黏度。同时,该纤维模型不仅无需迭代约束来保持纤维之间的连接,而且用相对较少的椭球体来模拟大长径比纤维在运动时的变形情况,大大减少了计算机的工作量,提高了计算机运行效率。但该模型很难确定椭球体之间的纤维距离(需迭代方法),同时也忽略了纤维间的水动力作用。

2.3 圆柱杆链纤维模型

为了能够简化计算纤维间距离,Schmid等人[8]提出了一种圆柱体铰链连接而成的新纤维模型,如图13所示。该纤维模型通过N-1个铰链把N个刚性圆柱杆连接而成的圆柱杆链,链中每个杆(除杆N外)一端为半球形帽,另一端则是半球形窝。为了保证纤维弯曲和扭转时纤维表面的光滑,杆N两端都是半圆球形帽。圆柱杆长为l,直径为D,长径比为rpr≡l/D,链总长为L=Nl,纤维长径比rp=L/D。杆在铰链处可以转动和扭曲,因此可以模拟纤维在流场中运动时的弯曲和扭转变形,但是由于约束限制纤维链总长是不变的。

(16)

表1 不同纤维模型的对比分析

(17)

(18)

方程(18)中,第二项和第三项是作用在杆i质心的约束力力矩。

该纤维模型能模拟大长径比(rp=50～280)的纤维,并能模拟纤维在絮凝状态下的纤维特性和纤维间相互作用对纤维絮凝的影响,其纤维特性包含纤维柔软度、形状等因素,纤维间相互作用包含法向排斥力和静摩擦等作用,但其考虑因素不包括动摩擦和纤维间引力的影响,且假设纤维各向同性弯曲。此外,该模型也可模拟纤维在长程水动力作用下纤维在流场中的运动变形情况,但是对计算机要求较高。

3 总结及展望

通过上述的阐述,对各种纤维模型的适应范围、优越性和局限性进行对比分析,如表1所示。

由表1可知，刚性纤维模型忽略了纤维在流场中的运动变形,适用范围相对较窄；而在柔性纤维模型中,各模型虽都考虑了纤维的运动变形,但仍存在一些不足之处。Yamamoto圆球形纤维模型主要局限于低浓度、底剪切流条件下的纤维运动变形,且计算过程比较复杂；PaalSkjetne圆球链纤维模型忽略了纤维的惯性和纤维间的相互作用；椭球体链纤维模型局限性主要表现为难确定椭球体之间的纤维距离,同时也忽略了纤维间的水动力作用；圆柱杆链纤维模型忽略了动摩擦和纤维间引力作用对纤维运动变形的影响,且在模拟长程水动力作用下纤维变形情况时,计算机运算量较大。从纤维模型发展过程来看,纤维模型发展趋势应是在圆柱杆链纤维模型基础上进行改进与发展,模型将可能考虑到更多影响纤维运动的因素,更能客观真实地模拟纤维在流场中的运动变形。

[1]JefferyGB.TheMotionofEllipsoidalParticleslmmersedinaViscousFluid[J].Proc.Roy.Soc.LondonSer.A, 1922, 102: 161.

[2]BrethertonFP.Themotionofrigidparticlesinashearflowatlowreynolds[J].Number.J.FluidMech., 1962, 14(2): 284.

[3]FuPingle,ChenKefu.Thepulpfibersuspensionmultiphaseflowanalysisanditsphysicalmodel[J].GuangdongPulp&Paper, 1988, (2): 12. 付平乐, 陈克复. 纸浆纤维悬浮液的多相流动分析及其物理模型[J]. 广东造纸, 1988(2): 12.

[4]XiaoZongliang.ResearchonPaperSuspensionFlowMechanismandNumericalSimulationforNewtypeofHydraulicheadbox[D].Hangzhou:ZhejiangUniversity, 2006. 肖宗亮. 新型水力式流浆箱内浆料流动机理及数值模拟研究[D]. 杭州： 浙江大学, 2006.

[5]YamamotoS,MatsuakaT.AmethodfordynamicsimulationofrigidandflexibleFibersinaflowfield[J].J.Chem.Phys., 1993, 98(1): 644.

[6]SkjetneP,RossRF,KlingenbergDJ.Simulationofsinglefiberdynamics[J].J.Chem.Phys., 1997, 107(6): 2108.

[7]ROSSRF,KlingenbergDJ.Dynamicsimulationofflexiblefiberscomposedoflinkedrigidbadies[J].J.Chem.Phys., 1997, 106(8): 2949.

(责任编辑：常 青)

The Research Progress of Fiber Motion Model in Pulp Suspension

GAO Zhi-fu1,2,*ZHANG Feng1,2WANG San-gang1

(1.College of Light Industry and Energy, Shaanxi University of Science & Technology, Xi’an, Shaanxi Province, 710021;2.ShaanxiProvinceKeyLabofPapermakingTechnologyandSpecialtyPaper,Xi’an,ShaanxiProvince, 710021)

Fiber model is very necessary for applying computer simulation technology to simulate fiber motion characteristics in pulp suspension. At present, there are rigid fiber model and flexible fiber model at home and abroad. This paper briefly introduced the development of the fiber model, especially analysed the ideas of building rigid fiber model and flexible fiber model, discussed the advantags, limitation and application area of different fiber models.

fiber pulp suspension; fiber; model; simulation; fluid

高致富先生,在读硕士研究生；主要研究方向：制浆造纸设备及其自动化。

2015- 01- 16(修改稿)

TS71+2；TB322

A

0254- 508X(2015)05- 0064- 06