中国电子及通信设备制造业集聚效应的实证研究

郭 利 平

(中原工学院 经济管理学院，河南 郑州450007)

中国电子及通信设备制造业集聚效应的实证研究

郭 利 平

(中原工学院 经济管理学院，河南 郑州450007)

产业集聚可以产生规模经济效应，使地区经济获得更快的增长。分别选取全国以及东部、中部和西部地区的电子及通信设备制造业作为研究对象，对1990-2012年面板数据进行了集聚效应的实证研究，并构建了计量经济学模型。结果表明：中国电子信息设备制造业存在着较为明显的集聚效应，东部沿海地区、中部地区也存在着较为明显的行业集聚效应，而西部地区电子信息设备制造业的增长主要来源于资本投入的增加，而不是集聚效应的影响。

面板数据；集聚效应；区位熵；洛伦兹曲线

一、引言

大量相关企业在空间的集中会产生集聚经济，由于外部性与规模经济的存在，集聚经济可以产生较高效率，使当地经济获得更多优势和更快速的增长。经济集聚现象早已存在，但真正引起经济学家广泛关注的则是源于克鲁格曼(1991)[1]和波特(1990)[2]123-126的研究。而从20世纪90年代以来，国内产业集聚的研究也开始逐渐增多，但大多主要集中在国外理论、方法的阐述和介绍，实证性研究和定量分析明显偏少，而且大都属于描述性的分析，按照标准的统计学方法和经济学方法对集聚经济的研究并不多见。许多相关理论和经验研究表明，集聚经济往往影响生产效率(Segal[3]，1976；Capello[4]，2002)。国内学者就产业集聚的经济效应问题也进行了一些实证研究(吴学花[5]，2004；贺小莉[6]，2010；周慧[7]，2010)。由于中国电子与通信设备制造业集聚度较高，而FDI投入本行业又较多，加之本行业在中国市场规模较大，又是较为典型的技术密集型行业，因此，就中国电子及通信设备制造业的集聚效应进行实证研究，将具有重要的理论价值和现实意义。

二、 模型设定与数据选取

(一)模型设定

集聚经济可以对生产效率产生影响，国外学者通过构造生产函数，对此进行了许多实证性检验。最常用的检验方法是柯布-道格拉斯生产函数(Cobb-Douglas production function)方法，简称C-D方程。柯布-道格拉斯生产函数在一般生产函数的形式上进行了改进，并在函数方程中引入了技术因素，成为经济学中应用最广泛和最具代表性的一种生产方程模式，它在计量经济学与数理经济学等学科的研究与应用中都占有极为重要的地位。

C-D生产函数方程一般形式为：

Y=ALαKβ

(公式1)

其中，Y为生产产出，L和K分别是劳动投入要素和资本投入要素，A、α、β为三个方程参数。从短期看，产业组织与技术水平暂时不变时，如果劳动和资本投入要素改变，会导致总产出的改变；但从长期看，产业组织、技术水平一定会发生改变，特别是在转型中的中国，经济的市场化程度越来越高，产业组织发生了较大变化，技术扩散也不断出现，这种变化会最终影响各种生产要素的产出弹性，从而改变生产产出。

国际上通用的用C-D生产函数估计集聚经济分成两种方法：一种是用生产函数中的常数项大小来衡量集聚效应(Henderson[8]，1986；Mukkala[9]，2003)，另一种是将集聚程度作为一个单独变量纳入生产函数中，用集聚水平变量的指数大小来衡量产业集聚对生产的贡献度(Ciccone[10]，2002)。

本研究采用后一种C-D生产函数验证集聚对中国电子信息制造业生产的影响，模型如下：

Y=ALαKβQθ

(公式2)

其中，Y代表工业增加值，L代表劳动投入要素，K表示行业资本投入量，Q则代表反映集聚水平的因素，采用产业专业化水平即产业区位熵指标。为了消除异方差性和更好解释变量间的关系，方程两边同时取对数可以得到行业产出对劳动投入、资本投入和集聚水平的经济学模型：

lnY=lnA+αlnL+βlnK+θlnQ

(公式3)

方程中，α、β分别反映生产中劳动、资本对生产的贡献程度。θ表示在劳动要素和资本要素不变的条件下，产业在某地集聚程度变化对产出规模的影响，即集聚水平对产出的弹性。如果实证分析结果得出θ>0，便验证了集聚经济的存在，即在劳动与资本投入相同的条件下，地区产业集聚程度越强，其要素生产效率越高，θ值越大，集聚经济对当地经济的促进作用越强。如果θ=0，说明产业的集聚对生产要素的产出效率没有影响。如果θ<0，则说明产业的集聚对要素生产率影响为负。

(二)数据的选取

本研究主要针对中国电子信息行业的集聚效应进行分析，同时分析东部、中部和西部电子信息行业集聚效应及东中西三大地带电子信息行业集聚效应的差异。面板数据(Panel data)也称混合数据(Pool data) 或平行数据，是指在时间序列上取多个截面，在这些截面数据上同时选取样本观测值构成的样本数据，这种数据同时在时间维度和截面空间取得二维数据。面板数据模型是一类利用混合数据分析各个变量之间相互关系并预测其变化趋势的计量经济学模型。面板数据综合利用样本信息，可以减少多重共线性带来的不利影响，同时可以提供更多的自由度和更高的估计效率，使研究更加深入(易丹辉[11]292-295，2011)，因此，本研究利用面板数据对模型进行估计。

由于宁夏、青海和西藏的电子信息产业微小，而且统计不完全，因此本研究中，我国电子信息集聚效应回归模型研究范围是27个省级行政区，其中，东部电子信息产业集聚效应分析区域11个，分别是辽宁、北京、天津、河北、山东、江苏、上海、浙江、福建、广东和海南；中部电子信息制造业集聚效应研究区域8个，分别是山西、吉林、黑龙江、江西、河南、安徽、湖北和湖南；西部电子信息制造业集聚效应研究区域也是8个，分别是陕西、贵州、云南、新疆、甘肃、内蒙古、广西和四川(四川与重庆合为一个研究单元)，因此，面板数据涵盖了1990-2012年27个省级行政区数据。由于缺少1995年、1996年和1998年三年的相关数据，面板数据只包含了20年的数据，其中，电子信息工业增加值①来源于1991年至2013年的《中国统计年鉴》和《中国工业经济统计年鉴》，资本投入K采用固定资产净值，劳动投入L采用全部从业人员年平均人数，产业区位熵Q由计算所得。

三、实证分析

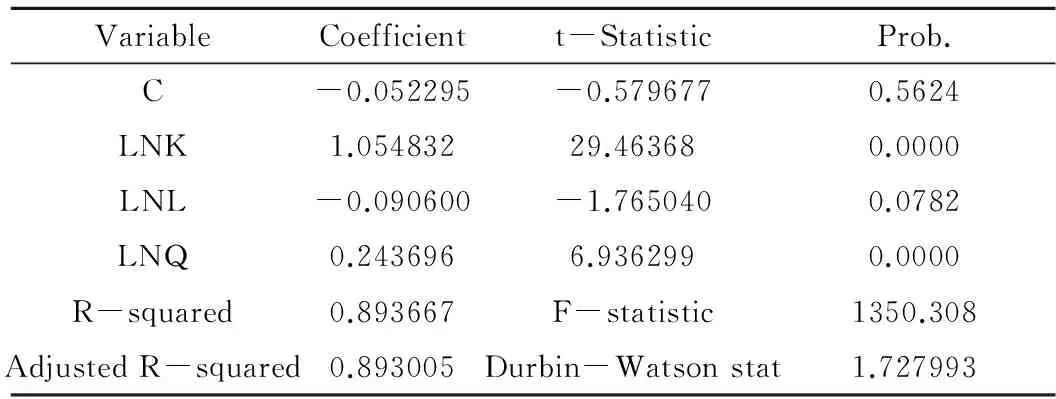
表1 中国电子信息行业集聚效应回归结果

根据中国27个地区电子信息产业变量在1990-2012年的样本观测值，用经济计量软件Eviews6.0对方程模型进行混合回归分析，可以得出中国电子信息行业集聚效应的计量经济模型(见表1)。

表2 中国东部地区电子信息行业集聚效应回归结果

根据中国东部11个省市电子信息产业变量在1990-2012年的样本观测值，用经济计量软件Eviews6.0对方程模型进行混合回归分析，可以得出东部电子信息行业集聚效应的计量经济模型(见表2)。

根据中国中部8个省市电子信息产业变量在1990-2012年的样本观测值，用Eviews6.0软件对方程模型进行混合回归分析，可以构建中国中部电子信息行业集聚效应的计量经济模型(见表3)。

表3 中国中部地区电子信息行业集聚效应回归结果

根据中国西部9个省市区电子信息产业变量在1990-2012年的样本观测值，用Eviews6.0软件对方程模型进行混合回归分析，可以得出中国西部电子信息行业集聚效应的计量经济模型(见表4)。

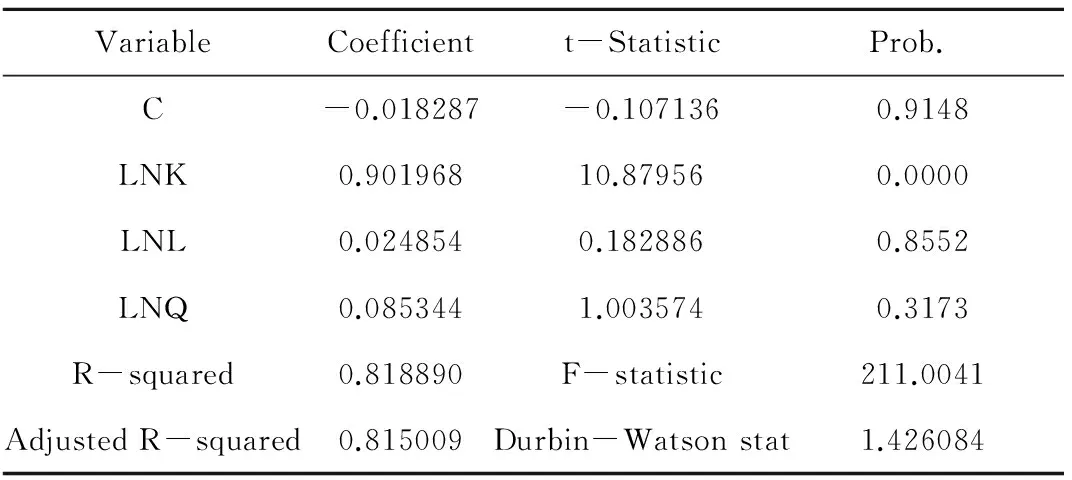
表4 中国西部地区电子信息行业集聚效应回归结果

四、结论

根据以上实证分析结果，我们可以得出如下基本结论。

第一，中国电子信息产业集聚效应模型可以表达为：LnY=-0.052295+1.054832LnK-0.090600LnL+0.243696LnQ。

根据表1，我们知道，LnL没有通过5%的显著性检验，但通过了10%的显著性检验，而LnK和LnQ都通过了1%的显著性检验，F值为211.004，说明整个方程系数通过了1%的显著性检验，模型整体显著；而调整后的R2为0.815，表明模型方程的拟合优度较高。

图1 中国电子信息设备制造业洛伦兹曲线

根据方程可知，劳动投入对产出影响很小，而资本要素对中国电子信息制造业产出贡献度较大。资本投入弹性系数为1.055，资本投入每提高1倍，产业产出将提高1.055倍。同时，区位熵弹性系数为0.244，意味着电子行业专门化系数提高1倍，在劳动要素和资本投入等条件不变的情况下，产业产出将提高24.4%。2012年，中国电子信息业是高度集聚行业，主要集聚在三个地区：广东、江苏和上海。这三个地区产出占全国的69.47%。观察洛伦兹曲线，电子信息制造业2012年比1990年集聚度更高(见图1)。其中最集聚地区是广东，区位熵最高，为2.847，固定资产净值占全国4.19%，劳动就业人数占全国6.93%，产出却占全国34.98%。这很大部分归功于规模经济和集聚效应。

第二，东部地区电子信息产业集聚效应模型可以表达为：LnY=-0.178584+1.075528LnK-0.034286LnL+0.224913LnQ。

根据表2，LnL没有通过10%的显著性检验，而LnK和LnQ都通过了1%的显著性检验，F值为617.697，表明整个模型系数通过了1%的显著性检验。而调整后的R2为0.904，表明模型的拟合度较好。

图2 东部地区电子信息设备制造业洛伦兹曲线

根据方程可知，劳动投入对产出影响很小，而资本投入对产出的贡献率较大。资本投入弹性系数为1.075，资本投入每提高1倍，产业产出将提高1.075倍。同时，区位熵弹性系数为0.225，意味着电子行业专门化系数提高1倍，在资本要素和劳动要素等条件不变前提下，电子信息制造业产出将提高22.5%。2010年，东部电子信息业是高度集聚行业，也主要集聚在广东、江苏和上海三个地区，这三个地区产出占全国的69.47%。东部地区的海南、河北地区集聚水平则较低。东部地区电子信息制造业2012年比1990年集聚度更高(见图2)。

第三，中部地区电子信息产业集聚效应模型可以表达为：LnY=0.141943+1.126920LnK-0.307637LnL+0.433230LnQ。

根据表3可知，LnL通过了1%的显著性检验，而LnK和LnQ也都通过了1%的显著性检验，F值为198.721，表明回归方程通过了1%的显著性检验。模型调整后的R2为0.806，表明估计模型的拟合优度较好。

根据方程，中部地区劳动投入对产出影响有负效应，中部劳动力丰富，过多的劳动投入导致管理和效益低下，对产业产出有一定抑制作用；相反，资本投入要素对产出的贡献率较大。资本投入弹性系数为1.127，资本投入每提高1倍，产业产出将提高1.127倍。同时，区位熵弹性系数为0.433，意味着在劳动要素和资本要素条件不变前提下，电子行业专门化系数提高1倍，产业产出将增加43.3%。中部地区区位熵对电子行业产出贡献度高于东部，是中部地区电子信息产业区位熵比较平均所致。从洛伦兹曲线分析，中部电子信息制造业2012年比1990年集聚度更高(见图3)。

图3 中部地区电子信息设备制造业洛伦兹曲线

第四，西部地区电子信息产业集聚效应模型可以表达为：LnY=-0.018287+0.901968LnK+0.024854LnL+0.085344LnQ。

根据图4可知，LnL和LnQ没有通过10%的显著性检验，而LnK通过了1%的显著性检验，F值为211.0041，整个回归模型通过了1%的显著性检验。方程调整后的R2为0.819，表明回归模型的拟合优度较好。

图4 西部地区电子信息设备制造业洛伦兹曲线

根据方程，劳动要素和区位熵都没有通过10%的显著性检验，说明劳动要素和区位熵对电子产出没有太大影响，两者的弹性系数也不高，而资本要素对行业产出的贡献率较大。资本投入弹性系数为0.902，资本投入每提高1倍，产业产出将提高0.902倍。西部资本弹性系数最小，低于全国水平和东部地区以及中部地区，说明资本对电子产业产出要小于其他地区资本要素的贡献率。而区位熵没有通过显著性检验，说明集聚效应在西部地区产业产出方面几乎没有太大影响，西部地区电子产出规模的增加主要来源于资本要素的投入。同时，西部电子信息制造业2012年比1990年集聚度更高(见图4)。

注 释：

①2008年前的《中国工业经济统计年鉴》有工业增加值统计数据，而从2009年开始不再统计此数据，因此，2008-2012年三年的电子信息工业增加值按照各省市区当年工业总产值比例计算。

[1]Krugman, P.Increasing Returns and Economic Geography[J].Journal of Political Economy, 1991,99 (3).

[2]Porter, E.M.The Competitive Advantage of Nations[M].New York: The Free Press,1990.

[3]Segal, D.Are There Returns to Scale in City Size?[J].Review of Economics and Statistics, 1976(58).

[4]Capello, R.Entrepreneurship and spatial externalities: theory and measurement[J].The Annals of Regional Science,2002,36(3).

[5]吴学花,杨蕙馨.中国制造业产业集聚的实证研究[J].中国工业经济,2004(10).

[6]贺小莉,王洪武,朱磊.基于面板数据的天津市工业集聚效应的测算与分析[J].统计与决策,2010(14).

[7]周慧,曹广喜.经济集聚与经济增长的空间计量分析[J].当代财经,2010(9).

[8]Henderson, J.V.Efficiency of resource usage and city size[J].Journal of Urban Economics, 1986(19).

[9] Mukkala, K.Agglomeration Economies in the Finnish Manufacturing Sector[J].43rd Congress of the European Regional Science Association 27-30, August 2003, Yyväskylä-Finland.

[10]Ciccone, A.Agglomeration Effects in Europe[J].European Economic Review ,2002,46(2).

[11]易丹辉.数据分析与EViews应用[M].北京:中国人民大学出版社,2011.

【责任编辑：李维乐】

2015-06-02

河南省软科学研究计划项目“河南省加快培育和发展战略性新兴产业研究”(编号：152400410601)。

郭利平(1970—)，男，河北宣化人，副教授、博士，上海财经大学应用经济学博士后，主要从事区域经济与国际贸易研究。

F407.63

A

1672-3600(2015)10-0107-04