溪洛渡特高拱坝初蓄期应力应变监测资料分析

商 峰，邱永荣 ，卢正超，范 哲

（1.中国水利水电科学研究院结构材料研究所，北京，100038；2.流域水循环模拟与调控国家重点实验室，北京，100038）

0 引言

溪洛渡水电站位于四川省雷波县和云南省永善县接壤的金沙江峡谷段，是一座以发电为主，兼有拦沙、防洪和改善下游航运等综合效益的大型水电站。溪洛渡水电站枢纽由拦河坝、泄洪、引水、发电等建筑物组成。拦河坝为混凝土双曲拱坝，建基面最低高程324.5 m，坝顶高程610 m，最大坝高285.5 m，2014年3月6日全线浇筑到坝顶。左、右两岸布置地下厂房，电站总装机1 386万kW，多年平均发电量571.2亿kW·h。

溪洛渡水电站设计正常蓄水位600 m，死水位540 m，汛期限制水位560 m，总库容126.7亿m3，调节库容64.6亿m3。初次蓄水分两个阶段进行：2013年5月4日，坝身3、4号导流底孔下闸，水库启动初期蓄水，6月23日蓄至水位540 m，12月顺利抬升至水位560 m，完成第一阶段蓄水目标。2014年8月21日，水库正式启动第二阶段蓄水，起蓄当日水位574 m，8月26日蓄至水位580 m，9月28日抬升至正常蓄水位600 m。

溪洛渡拱坝是继小湾、锦屏一级之后我国建成的第三座300 m级特高拱坝，也是目前世界上最高的几座混凝土坝之一。由于国内外可借鉴的经验相对较少，拱坝在建设和初次蓄水运行过程中的工作性态一直受到行业内专家、学者高度重视。随着计算机硬件和有限元计算方法的快速发展，朱伯芳院士等提出通过“数字监控”方法[1]分析、监控特高拱坝的真实工作性态[2]，有力地支撑了我国特高拱坝的建设。同时，传统的大坝安全监测资料分析方法仍然可以作为有益的补充，通过分析埋设在大坝内部的仪器的观测结果，为拱坝的安全监控、特别是应力应变的监控提供依据。

溪洛渡拱坝内共埋设了145组应变计组，包括六向应变计组69组、五向应变计组66组、三向应变计组10组。应变计组集中布置在334.2 m、442.2 m、481.2 m等高程坝体内靠近上游坝面、中部和靠近下游坝面的位置。拱坝内同时布设了162支配套无应力计，用于监测混凝土的无应力变形。依据拱坝内埋设的应变计组实测资料（截至2014年10月5日），计算分析拱坝在初蓄期的应力应变性态，进而评估大坝运行的安全性。

1 应力应变资料分析方法

实际混凝土结构内某一点的总应变包含两个部分：一部分是荷载和内部约束引起的应变，称为应力应变；另一部分是自由体积变形引起的应变，称为无应力变形。因此，依据实测应变资料计算应力时，需要首先从总应变中扣除无应力变形[3]。

1.1 无应力计分析

混凝土的无应力变形包括混凝土温度、湿度变化引起的变形和胶凝材料水化引起的自生体积变形，对各测点配套无应力计监测结果进行回归分析，求得测点附近混凝土的无应力变形。其回归方程的形式如下：

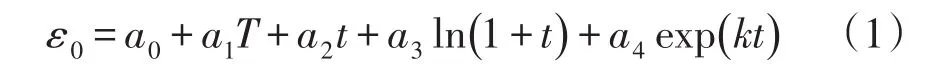
式中：T表示无应力计测点温度；t表示测时距分析起始日期的时间长度（d）；a0、a1、a2、a3、a4为回归系数，其中a1为混凝土的线膨胀系数；k=-0.01。方程中与时间t相关的项涵盖了湿度变化引起的变形和自生体积变形。依据（1）式和测点处应变计组各支应变计的温度平均值，计算得到该测点处任意时刻的无应力变形。

1.2 应变计组计算

根据应变计组中各支应变计的空间位置关系，可以计算得到测点处的三向正应变。一般地，三向应变计组和五向应变计组的布设在工程中较为常见，而六向应变计组则较少见，国内仅二滩拱坝曾经采用[4]。如图1所示，以A型布设的六向应变计组为例，推导六向应变计组对应测点处的正应变计算公式如下。

空间中任意方向的正应变ei与局部坐标系中的应变分量关系为：

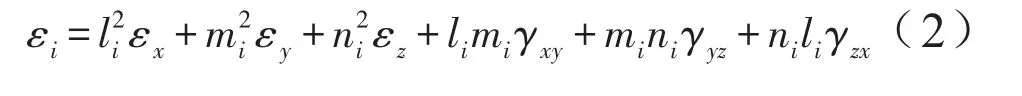
式中，li、mi、ni表示应变ei的方向余弦。Ozxy表示测点处的局部坐标系，z表示梁向，x表示拱向（指向左岸为正），y表示径向。正应变以拉为正，压为负。剪应变的符号以使所在平面两坐标轴夹角减小为正。利用（2）式对六向应变计组建立六元一次方程组，求解方程组得：

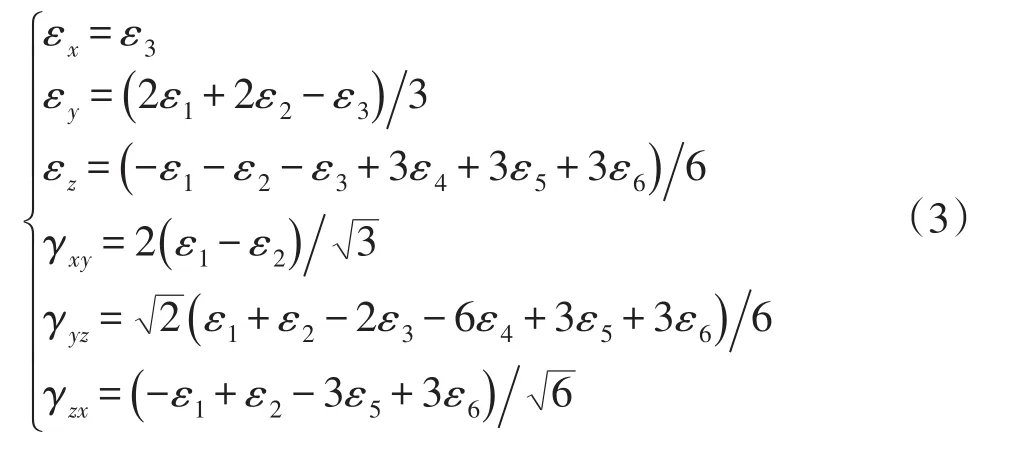
式中，ε1、ε2、ε3、ε4、ε5、ε6表示各支应变计应变测值。

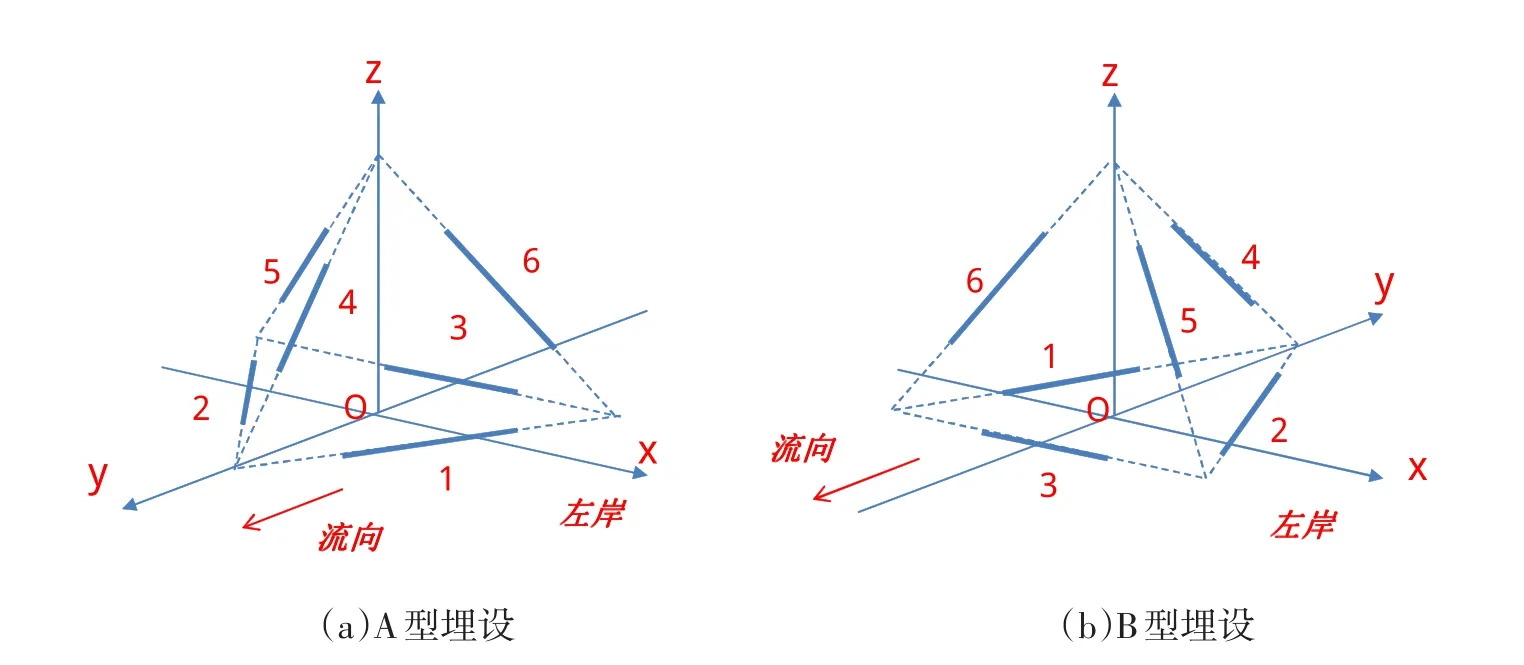
图1 溪洛渡拱坝内六向应变计组的布设方式Fig.1 Setting of the six-directional strain gauges inside the Xiluodu arch dam

求得测点处应变矩阵后，首先扣除无应力变形，再依据变形法[5]计算混凝土的徐变应力。上述计算流程中，对于五向应变计组，需要进行应变不平衡量检查，消除由于安装埋设质量带来的误差。当布置于同一平面的四支应变计有一支失效后，仍能按平面应力或平面应变进行应力计算，多于一支失效则不再能进行应力计算。对六向和三向应变计组，则不能进行不平衡量检查，只要有一支失效就不再进行应力计算。详细的不平衡量检查方法参见参考文献[6]。

2 溪洛渡拱坝应力计算成果

2.1 应力发展过程

图2显示了截至2014年10月5日拱坝拱冠梁坝踵附近（334.2 m高程上游侧）三向徐变正应力的计算结果，图中同时绘出了上游水位和应变计组的温度测值过程线。

从图2可以看出，通水冷却阶段，坝踵混凝土主要受到拉应力的作用，且拉应力值较小（除个别测值外，大多不超过1.0 MPa）；通水冷却结束后，坝踵逐渐向三向受压状态发展。

其中，蓄水前施工期随着坝高增加，梁向压应力增长较快，2013年5月4日梁向应力为-9.63 MPa；随着上游水位的抬高，梁向压应力减小。2013年5月4日～6月23日第一阶段蓄水过程中，梁向压应力减小1.37 MPa。此后，梁向应力受水位波动影响有所变化，至2013年12月9日第一阶段蓄水结束，梁向应力为-8.29 MPa。2014年8月21日～10月5日第二阶段库水位抬高过程中，梁向压应力减小0.32MPa，2014年10月5日梁向应力为-8.07 MPa。

同时，随着库水位的抬高，拱向压应力逐渐增加。2013年5月4日拱向应力为-2.36 MPa，2013年5月4日～6月23日第一阶段蓄水过程中，拱向压应力增加0.65 MPa。2013年12月9日第一阶段蓄水结束，拱向应力为-3.63 MPa。2014年8月21日～10月5日第二阶段库水位抬高过程中，拱向压应力增加0.29 MPa，2014年10月5日拱向应力-5.18 MPa。

蓄水过程中，径向应力的变化规律性不显著，压应力有缓慢增加的趋势。2013年5月4日径向应力为-1.71 MPa，2013年5月4日～6月23日第一阶段蓄水过程中，径向应力变化-0.13 MPa。2013年12月9日第一阶段蓄水结束，拱向应力为-1.96 MPa。2014年8月21日～10月5日第二阶段库水位抬高过程中，径向压应力增加0.74MPa，2014年10月5日径向应力-2.57 MPa。第二阶段蓄水过程中测值波动较大，测值可靠性略低。

2.2 应力分布规律

选取2014年10月5日前后各测点的应力计算值，绘制典型坝段的应力等值线分布图和应力增量等值线分布图。绘图时，以各测点为控制点，拱坝内其他区域应力采用径向基函数法插值计算得到。图3显示了18号坝段梁向应力分布和从2013年5月4日蓄水至今的梁向应力增量分布。

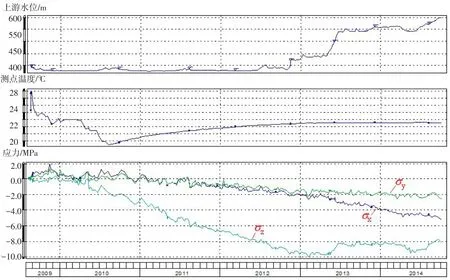
图2 溪洛渡拱坝拱冠梁坝踵（S6-18-1）应力发展过程Fig.2 Process of stress development at the dam heel measured by monitoring point S6-18-1

图3 溪洛渡拱坝18号坝段应力分布图Fig.3 Distribution of the stress at the block 18 of Xiluodu arch dam

可以看到，受拱坝倒悬体型影响，拱冠梁断面上游侧梁向压应力较大，下游侧梁向压应力较小；高程越高，上游侧梁向压应力越小。由于18号坝段481.2 m高程以上没有测点，因此，坝顶附近根据插值计算得到的应力精度较低。蓄水后，坝踵附近梁向压应力减小，坝趾附近梁向压应力增加；受拱坝倒悬体型影响，387.0 m高程以上上游侧梁向压应力增加，下游侧梁向压应力减小；387.0 m高程以上梁向压应力的变化幅度较小。

2.3 统计模型分析

大坝安全监测领域中的一项重要内容是通过建立合适的数学模型，对实测值进行回归分析，分离出不同的影响因子，进而分析时效因子的发展趋势，从而判断大坝的安全性态。应力应变监测是混凝土坝安全监测的重要组成部分，对评价大坝在初蓄期的工作性态尤其重要[3]。这里选择应力应变统计分析的数学模型如下：

其中，σz表示坝踵的梁向应力；σw表示水压分量；σT表示温度分量；σt表示时效分量。则，

式中，Hw表示库水位；H0表示建基面高程；ai表示待定参数。

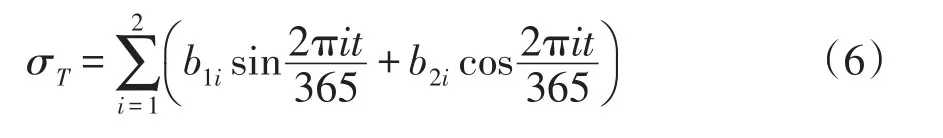
式中，t表示时间；b1i、b2i表示待定参数。

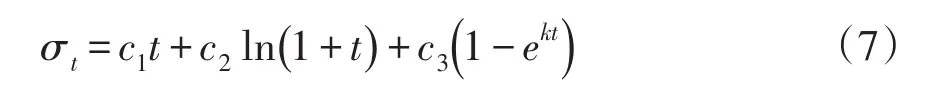
式中，ci表示待定参数；k=-0.01。

对2013年5月4日以后18号坝段坝踵梁向应力发展过程进行多元线性回归分析，结果如图4所示。回归分析的复相关系数R=0.943 3，离散系数S=0.161；回归精度良好。

可以看到，18号坝段坝踵梁向应力发展与水位有良好的相关性，截至2014年10月5日，水位分量为3.18 MPa；温度分量为周期性分量，冬季温度分量为拉应力，夏季温度分量为压应力，截至2014年10月5日，温度分量为0.14 MPa。由于2013年5月拱坝尚未浇筑到坝顶，时效分量内包括了部分自重应力的影响，2014年3月拱坝浇筑到坝顶后，时效分量的发展逐渐趋于平缓，截至2014年10月5日，时效分量为-1.32 MPa。

3 与有限元仿真计算结果的对比

影响拱坝初蓄期应力的因素众多，其中，荷载因素主要包括温度荷载、自重、初蓄期水压荷载等。荷载过程受浇筑、温控和蓄水过程控制，同时，拱坝应力与混凝土材料特性，如徐变、线膨胀系数、自生体积变形等因素紧密相关。另一方面，由于横缝灌浆的影响，封拱后各坝段应力还与拱坝体型、坝基坝肩地质条件等因素有关，因而难以直观判断依据应变计组进行应力计算的分析结果的合理性。所以，需要将应变计组应力计算分析结果与有限元仿真计算结果加以对比，进一步讨论分析应变计组监测和应力计算成果。这里选用中国水利水电科学研究院结构材料研究所大坝仿真室提供的有限元仿真计算结果[7，8]。仿真计算严格考虑了大坝施工过程和环境地质条件等因素，以此来模拟大坝在施工期的真实工作性态，该方法在国内多座在建、已建拱坝施工期温度控制过程中得到了应用，并取得较好的结果，具有一定的参考价值[2]。

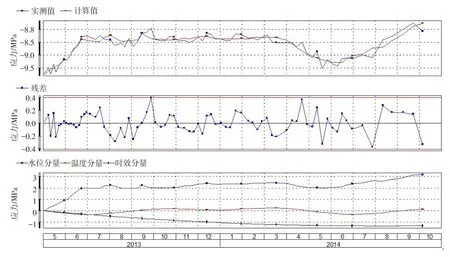
图4 溪洛渡拱坝拱冠梁坝踵（S6-18-1）应力发展过程Fig.4 Process of stress development at the dam heel measured by monitoring point S6-18-1

分别选取蓄水前（2013年5月3日）和蓄水后（2013年6月23日、2014年10月5日）三个日期对应的大坝工作性态仿真计算结果，与监测资料分析成果对比如表1所示。可以看到，监测资料分析得到的应力发展过程与有限元仿真计算结果吻合良好，表明目前溪洛渡大坝内埋设的应变计组的监测结果是基本可信的，进行的应变计组应力计算分析成果是可靠的。

表1 18号坝段坝踵梁向应力与有限元仿真计算结果的对比Table 1 Comparison between the measured stress and the calculated results by finite element simulation of the dam heel at block 18

4 结语

依据溪洛渡特高拱坝内埋设的应变计组的实测资料（截至2014年10月5日），计算拱坝在初次蓄水阶段的应力状态，分析其发展过程，并和有限元仿真计算结果相对比。结果表明，拱坝应力发展过程和应力分布符合一般认识规律，库水位抬升至正常蓄水位后，坝踵和坝趾仍都处于受压状态，拱坝在初蓄期工作性态正常。

大坝在初蓄期往往会暴露出很多问题，而初蓄期后的正常运行阶段，工作性态一般比较平稳。因此，初蓄期是对大坝设计、施工质量的综合检验，而大坝安全监测资料则是最重要的依据，所以，需要高度重视大坝在达到正常蓄水位之后3年内的安全监测资料分析工作。

[1]朱伯芳,张国新,贾金生,等.混凝土坝的数字监控——提高大坝监控水平的新途径[J].水力发电学报，2009,28(1):130-136.

[2]张国新,刘毅,朱伯芳,等.高拱坝真实工作性态仿真的理论与方法[J].水力发电学报，2012,31(4):167-174.

[3]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社，2003.

[4]张进平,庄万康.二滩拱坝施工期实测资料分析报告[R].中国水利水电科学研究院，1997.

[5]朱伯芳.大体积混凝土温度应力与温度控制（第二版）[M].北京:中国水利水电出版社，2012.

[6]储海宁.混凝土坝内部观测技术[M].北京:水利电力出版社，1989.

[7]中国水利水电科学研究院.溪洛渡拱坝蓄水工作性态评价与风险预警分析报告（水位已蓄至540 m高程）[R].2013.

[8]中国水利水电科学研究院.溪洛渡拱坝蓄水工作性态评价与风险预警分析报告（水位已蓄至600 m高程）[R].2014.