电力有源滤波器谐波检测算法
宋秉虎,王明晖
(1.国网甘肃省电力公司,甘肃兰州730000;2.中国航天科工集团二院,北京100854)
电力有源滤波器谐波检测算法
宋秉虎1,王明晖2
(1.国网甘肃省电力公司,甘肃兰州730000;2.中国航天科工集团二院,北京100854)
随着电力电子技术的快速发展,大量的开关器件被应用于电力控制中,给电网带来不可忽视的谐波。在众多谐波补偿装置中,电力有源滤波器是一种比较理想的滤波装置,它可以实时地检测出电网中的谐波电流,由补偿装置发出补偿电流,从而达到谐波抑制的目的。如何快速准确地检测出电网中复杂的谐波电流成为一个重要的研究内容。提出一种基于小波变换的无功电流与谐波检测方法,该方法既能检测稳态信号,又能检测出瞬态变化信号,通过仿真和实验结果,验证了该方法优秀的分析能力。
电力有源滤波器;谐波检测;小波变换
0 前言
从20个世纪二三十年代开始,德国首次提出了静态整流器引起的电流波形畸变问题,也正是从那时开始,谐波这一问题引起人们的注意。谐波是频率为基波整数倍的信号,谐波的存在给电网带来了很多不利的影响,如影响设备正常工作,产生附加损耗,使设备过热,产生误动作,降低设备的寿命等。随着电力电子技术的发展,大量的开关器件被应用于电源装置和电机调速中,在为工业设备带来高效良好控制手段的同时,也给电网带来了不可忽视的高次谐波。近几年,针对传统谐波抑制的各种弊端,有源滤波技术被广泛关注。有源滤波技术的基本原理是从电网中实时检测出谐波电流的信息,由补偿装置发出与谐波电流大小相等、方向相反的补偿电流,从而达到谐波抑制的目的。电力有源滤波器是一种可以动态补偿电网谐波的装置,弥补了传统谐波抑制的诸多不足,谐波检测算法的选择对于谐波抑制的效果起着至关重要的作用,只有实时准确地检测出当前时刻电网中的谐波并且给予补偿,才能达到良好的谐波抑制效果。目前,在各种有源滤波设备中,应用最广泛的是基于瞬时无功理论的谐波检测方法,在分离各次谐波、进行谐波分析方面,应用最广泛的是基于快速傅里叶变换的谐波检测方法及其改进。这两种算法对于稳定信号都具有很好的检测能力,但是对于频率不变、幅值实时变化的时变信号的分析能力具有很大的局限性。针对这一情况,结合小波变换良好的时域和频域分析能力,提出了一种基于小波变换的谐波检测方法,可以有效地检测稳定信号和时变信号,对谐波抑制有较好的效果。本研究将对三种检测算法进行详细的研究,并通过仿真和实验,分析其优缺点。
1 基于快速傅里叶变换的谐波检测算法
法国科学家傅里叶提出,任意一个函数x(t)都能被分解成无穷多个不同频率的正弦信号的和,这也是谐波分析的基本原理。傅里叶变换基本计算式为
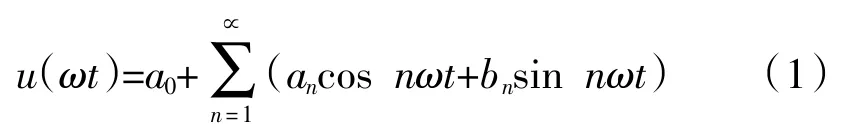
式中

基本的傅里叶变换需要大量的计算,耗费许多时间,虽然分析结果精确无误,但往往无法投入到实际环境中,原因在于其较差的时效性。1965年美国Cooly和Tukey两人提出了傅里叶变换的快速算法,即快速傅里叶变换(FFT),使得傅里叶变换的运算量降为原来的一半,从实验室研究最终走向了工业实践。FFT的基本原理是对信号进行离散处理后,使其变成数量序列,由快速傅里叶变换算法计算出各次谐波的幅值及相位等参数。
快速傅里叶变换算法分为两种:时间域抽取法和频率域抽取法。两个算法在时间复杂度和空间复杂度上都一样,只是最后计算的结果排列顺序有所不同。本研究采用的是时间域抽取FFT算法。对于FFT运算,通常用蝶形图来表示,比如对于N=8的FFT,其运算过程如图1所示。
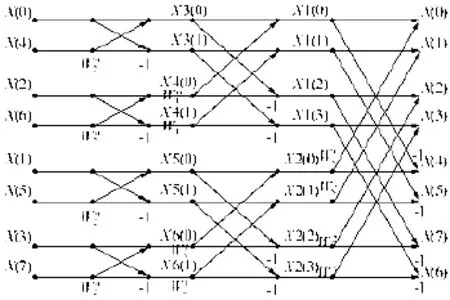
图1 N=8点的FFT蝶形运算
目前快速傅里叶变换算法已经相当成熟,Ti公司为DSP程序开发提供了由汇编语言编写的FFT库函数,程序员在编写程序时,只要进行适当的配置,就可以直接调用。该库函数计算精度高,实时性好,时间复杂度为O(N)=O(N·Log2N),在实际工程应用中,三相电流128点的FFT运算完全可以在一个基波周期内完成,因此对于稳定信号的分析,FFT能够达到很好的谐波检测效果。
本研究使用sin库函数模拟产生一个包含直流分量、基波、二次谐波和三次谐波的信号,用FFT计算后看是否在相应的点上出现正确的结果,对其正确性进行验证。输入波形采样128点:
for(i=0;i<FFT_Size;i++)
InBuffer[i]=2+6*sin(2*PI*i/FFT_Size+1.254*PI)+220*sin(2*PI*i*2/FFT_Size-2.5*PI)+20*sin(2*PI*i*3/ FFT_Size+0.5*PI);
计算结果如图2、图3和表1所示。
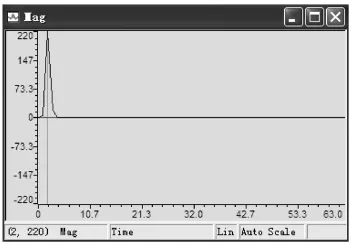
图2 幅值计算结果
根据FFT分析结果可知,FFT计算结果正确,精确度达到99.9%,完全满足谐波计算的精确度要求。但是FFT的缺点是:当分析点数比较多时,其计算时间较长,造成较大的延时,给整个系统的控制增加困难,影响谐波抑制效果。快速傅里叶变换只能直接求出信号的幅值和频率,若想求出谐波信号的波形,需要再次进行转换,这就又需要计算量和运算时间。相比之下,基于瞬时无功功率理论的谐波检测算法具有明显的实时性优势。
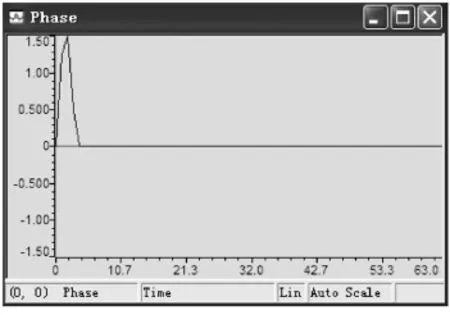
图3 相位计算结果
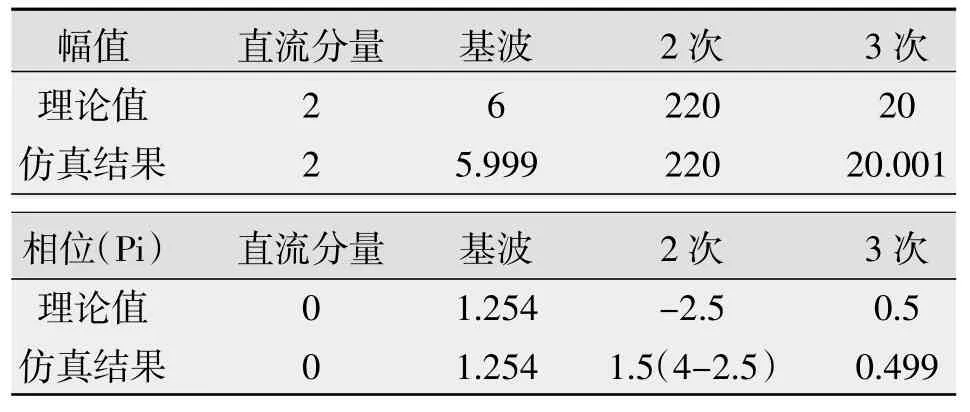
表1 幅值和相位计算结果分析
3 基于瞬时无功理论的谐波检测算法
1983年,日本学者赤木泰文首次提出了瞬时无功功率理论,此后,该理论经过不断的研究和完善,最终得以投入到实际的产品应用中。赤木泰文最初提出的理论又被称为pq理论,是以瞬时实功率p和瞬时虚功率q为基础,其不足之处在于没有对相关的电流量进行定义。以瞬时无功和瞬时有功电流为基础的理论进行研究。
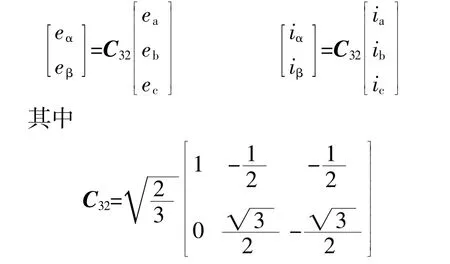
假设三相电路中电压和电流分别为ea、eb、ec和ia、ib、ic,对其进行坐标转换,求得两相瞬时电压eα、eβ和两相瞬时电流iα、iβ。
在如图4所示的α-β平面上,矢量eα、eβ和iα、iβ可以通过旋转分别合成为电压矢量e和电流矢量i,e=eα+eβ=e∠φe,i=eα+eβ=i∠φi。
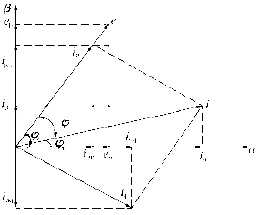
图4 坐标系中的电压、电流矢量
三相电路瞬时有功电流ip和瞬时无功电流iq分别为矢量i在矢量e及其法线上的投影。即ip=i cosφ,iq= i sinφ。ip、iq运算方式的原理如图5所示。
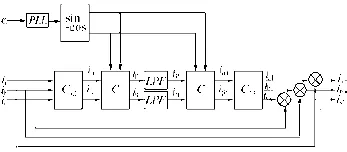
图5 i p、i q运算方式的原理
为了验证瞬时无功检测算法的检测性能,使用标准源产生一个含有三次谐波30%+三次谐波10%的三相电流信号,经过瞬时无功计算出其中的基波电流的波形,如图6所示。
由上述理论分析可知,瞬时无功谐波检测最后得到的是电网总的谐波信息,相比FFT分解得出各次谐波信息的运算量小了很多,在实时性上具有很大的优势,但是它不能得出某一次谐波的具体情况。另外,瞬时无功对电压和电流采集的同步性要求苛刻,即电压和电流采集值必须在同一时刻,否则无法保证算法结果的准确性。
4 基于小波变换的谐波检测算法
4.1 小波变换的特点
快速傅里叶变换和瞬时无功检测算法都可以准确检测稳定信号,但它们都有自己的不足:快速傅里叶变换只能得出各次谐波的幅值和相位信息,只具有频域分析能力,不能显示某一个时刻谐波信号的变化情况,也就是不具有时域分析能力;瞬时无功检测算法可以检测出电网中总的谐波情况,但不能检测出某一个特定频率的谐波信息。小波变换是一种时域和频域都局部化的分析方法,可以分析出某一个频率的谐波在某一个时刻的变化情况。小波是最短最简单的振动,其基本思想是用一系列函数去逼近一个信号,这一系列函数被称为小波函数系,它们是通过一个小波基函数伸缩和平移得到的。
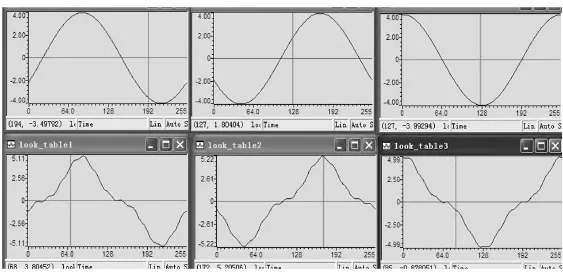
图6 瞬时无功计算出基波
小波变换是一种时域和频域都局部化的分析方法,它可以随着参数的设置调整时频窗口的大小,在信号频率较低的部分,具有较高的频率分辨率和较低的时间分辨率,在信号频率较高的部分,具有较高的时间分辨率和较低的频率分辨率,通过变换将时域信号的某个频率段的信号分离出来,同时体现信号的时间、频率和幅值特征,是时变信号的一种强有力的分析工具。小波变换也存在类似FFT一样的快速算法,快速算法的出现极大地扩宽了小波变换的应用领域。小波变换的时频窗如图7所示。
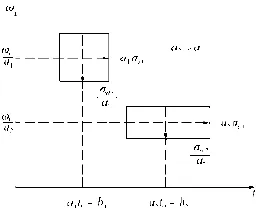
图7 小波变换的时频窗
目前,小波变换广泛应用于图形图像的压缩处理、地震信号检测等领域。在电力系统中,小波变换的应用主要涉及故障信号特征抽取、滤波去噪、故障测距定位、电力系统短期负荷预测和分布式电力系统继电保护等。由于傅里叶变换在分析含时变信号时的不足,小波变换就显得更加重要。
最初,小波变换有很多不足,如运算量巨大、延时较长影响其应用范围等,随着Mallat算法等快速算法的提出,小波变换的应用领域开始逐渐扩宽。近来,高速DSP和AD技术的发展促进了小波变换在电力系统谐波检测领域的应用。
4.1 M allat算法的基本原理
设Vj为L2(R)中一组相继的闭子空间,而Vj+1和Wj+1分别为低分辨率下的闭子空间,Aj为到Vj的正交投影子,而Dj为到Wj的正交投影子,则
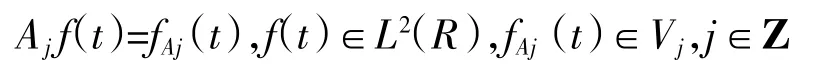
同理对Dj和Wj也存在着类似关系,假设Vj和Wj存在如下的关系
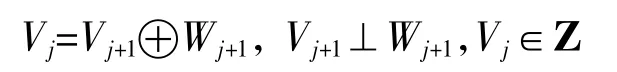
即Vj可以分解为Vj+1和Wj+1的和,则有
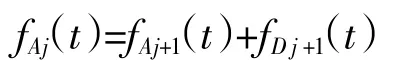
这就是Mallat算法的基本原理。
设f(t)为待分析的原始信号,其包括了基波和谐波信号,f(x)是原始信号经采样得到的离散序列,对f(x)进行多分辨率分析,有
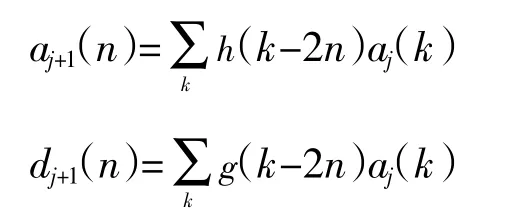
这就是Mallat算法的分解过程。aj(n)称为离散逼近信号,它包括信号的低频部分,大致描述了原始信号的变化趋势;dj(n)为离散细节信号,它包括信号的高频部分,能够反映信号的复杂变化情况。小波变换的多分辨率分析过程就是一个滤波的过程,通过分解,将原始信号按频率分开,其分解示意如图8、图9所示。
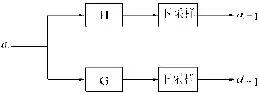
图8 Mallat算法信号分解过程
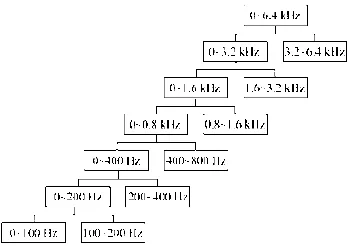
图9 M atlab算法信号分解过程
与分解过程相对应,重构过程是根据aj(n)和dj(n)构造部分信号的过程,其重构公式为
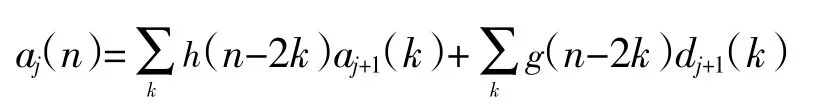
信号重构的示意如图10所示。
这样,信号经过多分辨率分析,不同频率的信号被划分到不同的频率段,然后用户根据不同的需求对特定的子频率段进行重构,即可求出不同频率的谐波。在分解层数合适的情况下,可以将低频部分近似地认为是基波信号,以此求出总的谐波信号,从而进行谐波抑制。
4.2 小波变换检测算法的仿真分析
电网中通常含有大量的谐波,但是比较平稳,使用常规的谐波检测算法都可以达到很好的效果。但是当电网出现异常时,电网中会出现幅值变化的信号,使用常规谐波检测算法无法准确地检测出其变化规律。小波变换就可以在这方面发挥它的优势,本研究在matlab中构造一个频率不变但是幅值衰减的信号,使用小波变换进行分析,然后再与FFT和瞬时无功检测算法的检测结果进行对比。
电流信号包含基波、3、7、5、11、13次稳态谐波,其幅值之比为22∶15∶5∶3∶3∶3,从起始时刻开始,30次谐波幅值按照指数规律衰减,其初始幅值为141 A,该瞬态信号波形如图11所示,电流信号波形如图12所示。

图11 瞬态信号波形
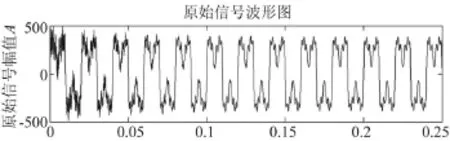
图12 电流信号波形
4.3 仿真结果与分析
为使频带划分效果更好,小波变换分析时选用的分析小波为db4小波,每个基波周期采样256点。由于只要求检测出瞬态分量和稳态分量,因此分解层数为4层。电流信号经过分解,最后得到高频和低频两部分。对高频部分进行重构,即可得到瞬态信号的波形,对低频部分进行FFT分析可以精确求得稳态谐波和基波的幅值和相位信息。小波分析的检测策略流程如图13所示。
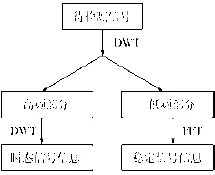
图13 检测策略流程
小波变换对高频部分进行重构后的效果见图14,FFT对低频部分进行分析得到的信息见图15。
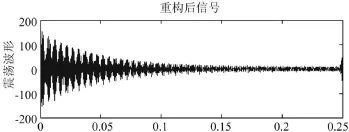
图14 高频瞬态信号重构波形
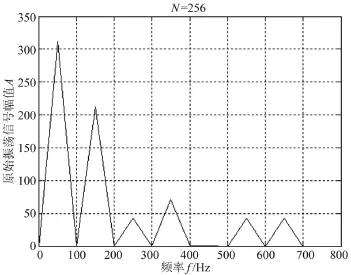
图15 低频稳定信号的FFT分析结果
结合图15可知,对于瞬态变化的信号,小波变换可以通过重构特定频段的信息还原出30次谐波的变化规律,虽然波形的精度不高,却能够反映出高次谐波的变化规律。对于低频部分,结合表2可知,使用FFT进行分析后能够精确地求出各次稳态谐波和基波的幅值信息。通过小波变换和FFT相结合的方法,可以实时准确地检测出谐波的信息。
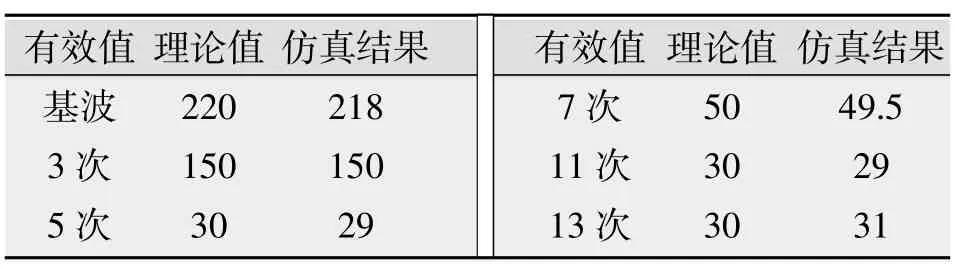
表2 仿真结果对比
如果单纯对原始信号进行FFT分析,分析结果如图16所示。对于稳态谐波信号,FFT可以准确地检测和分析出其幅值,能够有效地对反映谐波的情况,但是对于按指数规律变化的30次谐波,FFT只能检测出其初始的幅值,但是不能反映其变化规律。
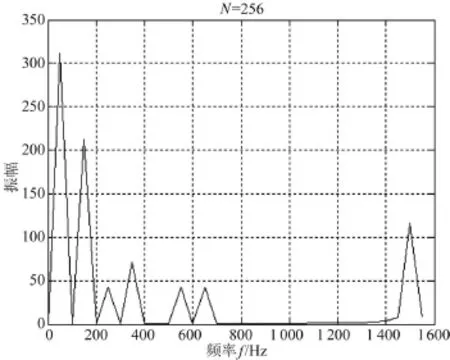
图16 电流信号的FFT分析结果
单纯对原始信号进行瞬时无功分析,结果如图17所示。由图17可知,瞬时无功检测算法可以求出总的谐波信号,但是对于某一个特定频率的谐波信号不能准确给出其信息,从分解出的谐波信号也很难看出其中存在幅值衰减的瞬态信号。
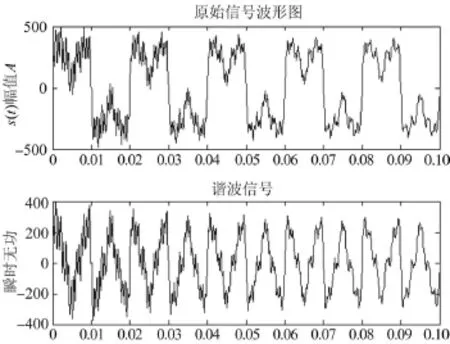
图17 电流信号的瞬时无功分析结果
综合以上三种检测算法的仿真结果与分析,小波变换检测算法可以准确地检测出瞬态变化谐波信号的变化规律,克服了瞬时无功和FFT在这一方面的局限性。小波变换在谐波检测方面具有很好的研究意义。
4.4 实验结果和分析
实验配电见图18,控制系统采用TMS320F28335,每基波周期采样256个点,信号采样频率12.8 kHz。
程序使用db小波对采样信号进行变换,根据前面的分析,分离出50Hz的基波信号需要进行7次分解和1次重构,程序实际运算时间很长,不能满足APF产品的实时性要求,但是对于已经采样得到的静态数据,小波变换能够准确地分离出其基波,实验结果如图19和图20所示。图中横坐标为采样点数,纵坐标为电流的瞬时值。根据仿真实验和实验结果可知,小波变换不仅可以求得瞬态变化信号,还能求得基波这样的稳定信号,具有很好的时域局部性和频域局部性。小波变换唯一的不足是其运算时间比瞬时无功和FFT都长,在实时性上没有优势。
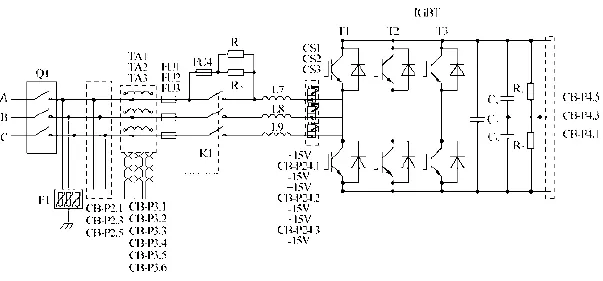
图18 实验配电电路
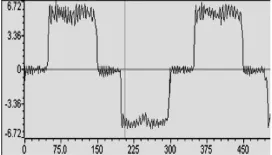
图19 程序采样信号波形
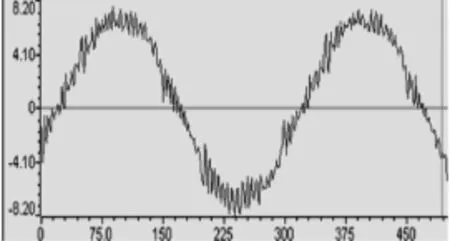
图20 小波变换分离出的基波波形
5 结论
针对FFT和瞬时无功对瞬态变化信号检测能力的局限性,提出了一种基于小波变换的谐波检测方法,该方法可以将信号按照不同频率进行划分。用户根据需求对特定频率段的信号进行重构,从而提取出某一特定频率的信号,观察其变化规律。最后对小波变换进行了仿真和实验,验证了小波变换对稳态信号和瞬态变化信号的检测能力。
[1]赵世廉.TMS320X24x DSP原理及应用开发指南[M].北京:北京航空航天大学出版社,2007.
[2]Albert H.Kaiser.Digital Signal Processing Using the Fast Fourier Transform(FFT)[M].GRINVerlagoHG,2007-12.
[3]苏奎峰,吕强,常天庆,张永秀.TMS320X281x DSP原理及C程序开发[M].北京:北京航空航天大学出版社,2008.
[4]李全利,刘长亮.CCS上FFT运算的实现[J].通信与信息处理,2009(02):59-62.
[5]李猛,李红.快速傅立叶变换(FFT)在数字信号处理器(DSP)上的实现[J].船舶防化,2007(01):34-37.
[6]夏雪.小波变换在不对称系统谐波检测中的研究[D].重庆:重庆大学,2006.
[7]徐永海,肖湘宁,杨以涵.小波变换在电能质量分析中的应用[J].电力系统自动化,1999(12):55-58.
[8]Teodorescu R,Blaabjerg F.Multilevel converter-a survey. EPE’99,1999,CD-ROM.
[9]Bhim Singh,KamalAl-Haddad.AReview of Active Filters for Power Quality Improvement[J].IEEE Trans on Industrial Electronics,1999,46(5):960-971.
[10]邵明,钟彦儒,余建明.基于小波变换的谐波电流的实时检测方法[J].电力电子技术,2000(02):44-47.
[11]J.vanWyk.Powerquality,powerelectronics and control[J]. European Conf.Power Electronics and Applications,1993(1):17-32.
[12]Habrouk M,Darwish M K,Mehta P.Active power filter.A review[J].IEEEProc ElectrPower Appl.,2000,147(5):403 -413.
[13]顾建军,徐殿国,刘汉奎,等.有源滤波技术现状及其发展[J].电机与控制学报,2003,7(2):127-132.
[14]戴朝波,林海雪,雷林绪.两种谐波电流检测方法的比较研究[J].中国电机工程学报,2002,22(1):80-84.
Harmonic detection algorithm of active power filter
SONG Binhu1,WANGMinghui2
(1.Gansu Electric Power Corporation,Lanzhou 730000,China;2.The 2th Institute,China Aerospace Science and Industry Group,Beijing100854,China)
With the rapid development of power and electron technology,a large number of switching devices are used in the power control,and brings to the power grid harmonic which cannot be ignored.Among the technologies of harmonic suppression and reactive compensation,the active power filter(APF)is themost famous.APF can timely detect the harmonic currentandmake compensation so as to increase the power quality.So themeasurement of harmonics is a very important research point.In view of this situation,power theory and harmonic detection algorithm based on discrete wavelet transform is introduced in order to extract harmonic signal information.
APF;harmonic detection;wavelet transform
TG434
A
1001-2303(2015)07-0028-07
10.7512/j.issn.1001-2303.2015.07.07
2014-12-15
宋秉虎(1970—),男,高级工程师,主要从事电力物资管理、供应链管理工作。

