人工神经网络预测混凝土柱屈服性能*

唐和生,李大伟，苏 瑜，赵金海

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.同济大学 结构工程与防灾研究所，上海 200092)

人工神经网络预测混凝土柱屈服性能*

唐和生1,2†,李大伟2，苏 瑜2，赵金海2

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.同济大学 结构工程与防灾研究所，上海 200092)

建立了一种基于人工神经网络的矩形混凝土柱屈服性能预测方法.该方法采用经验模型进行柱屈服性能影响因素的分析来确定该神经网络的输入参数，并通过敏感性分析验证了所选神经网络输入参数的合理性.为验证该方法的可行性与有效性，通过对PEER 210组矩形混凝土柱的屈服性能进行预测分析并与经验预测模型的预测结果进行比较.比较分析结果表明：神经网络预测结果与实验结果吻合程度远高于其他经验预测模型；同时也证实该方法在实验数据稀少的情况下为预测结构在地震作用下的性能提供一条新途径.

矩形混凝土柱；屈服位移；人工神经网络；预测模型

随着社会经济的发展，以及对近些年大地震的不断反思，基于性能的结构抗震设计已成为地震工程领域研究的热点问题和前沿发展方向，为众多国家的规程所提及或者采用(如FEMA273[1]，FEMA356[2]，ASCE41[3]和Eurocode8[4]).柱子作为实际结构中承受竖向荷载和抵抗水平荷载的关键构件，其屈服位移的合理评估对于性能化结构抗震设计中结构的动力响应、结构性能水准的评估和抗震延性设计有很大影响.综合以往对柱子屈服位移的研究，其定义不明确，经验理论模型预测结果离散度较大的特点，使柱屈服位移的合理取值成为一个亟待解决的问题.

对于柱屈服位移的定义，国内外研究者提出了不同的看法，如Park在文献[5]中总结了4种不同的定义方法，并推荐使用割线刚度的方法定义屈服位移.Panagiakos[6]认为判定柱屈服的条件是柱中纵向钢筋屈服或者混凝土发生严重的非线性行为，并在此基础上给出了对应的经验公式.Montes[7]基于柱中钢筋屈服,提出了对应不同强度等级钢筋的柱有效屈服曲率计算公式.Berry[8]等模拟了PEER[9]柱性能数据库中255根矩形截面混凝土柱的屈服位移.钱稼茹[10]亦对该数据库中144根剪跨比大于2的矩形柱考虑轴压比的影响进行回归分析，提出了修正的柱屈服转角表达式.蒋欢军[11]综合Berry[8]关于屈服位移以及Priestley[12]对于屈服曲率的定义，在计算屈服位移的公式中加入了考虑柱端钢筋滑移和柱子剪切变形影响的修正项.Peruš[13]基于Eurocode8[14]中柱屈服位移的定义，利用CAE方法对PEER柱性能数据库的柱屈服位移进行了预测.

柱屈服过程中钢筋和混凝土都发生了复杂的非线性行为，加之影响屈服性能的因素也非常多，上述基于经验理论的非线性拟合公式预测柱屈服性能时存在预测结果离散度非常大的问题.人工神经网络作为一种在数据稀少的情况下能够有效预测数据输入和输出关系的手段而进入研究者的视野.人工神经网络是以人类神经活动为基础而发展起来的一项新颖的计算手段，适合处理复杂线性及非线性映射问题.由于其强大的非线性映射能力，神经网络在工程领域被用于预测圆柱形混凝土柱约束状态的极限压应力和对应的压应变[15]，模拟金属疲劳裂纹开展速率[16].神经网络的其它工程应用还有如混凝土柱在弯曲失效模式下的极限变形预测[17]，边坡稳定性分析[18]，修正结构有限元模型[19]等.

本文基于经验理论模型对弯曲型混凝土柱屈服性能影响因素的研究，利用神经网络预测PEER柱性能库210组矩形混凝土柱的屈服性能，并以此来探讨神经网络对柱性能预测的可行性和有效性.通过对比神经网络的预测结果与实验结果以及经验理论模型估算结果,评价神经网络预测模型的效果.最后基于Carson敏感性分析方法验证所选神经网络输入参数的合理性并得到输入各参数对混凝土柱屈服位移的贡献程度.

1 经验模型预测实验数据库柱屈服转角

1.1 实验数据库

本文对弯曲型失效为主的柱屈服转角进行预测,在PEER[9]柱性能数据库中通过以下标准：1)柱子截面形状为矩形；2)柱子受往复荷载作用直至失效；3)柱子的实验失效模式为弯曲失效．选择210组实验数据，作为神经网络预测数据库.该预测数据库的主要属性参数范围如图1所示．

从图1中可看出本文所选数据库主要参数分布覆盖了常规设计的参数取值范围，具有广泛的代表性.

1.2 经验模型预测结果比较

本文采用Berry在文献[8]中如式(1)所示的屈服位移的定义:

(1)

式中：Ffirstyield为柱子首次屈服时的作用力，△firstyield为柱发生首次屈服时的位移；F0.004为混凝土应变达到0.004时作用力.上述屈服位移可由经验模型计算而得[20]：

(2)

图1 柱性能数据库的主要参数分布

实验值/%

表1 经验模型预测结果的实验验证Tab.1 Experimental verification of the empirical model

从图2和表1中可以看出，利用4种经验模型估算构件的屈服转角时，预测值与实验值的比值分布相当离散，ASCE41模型计算结果变异系数相对较小为0.443，而利用ACI318-08(b)变异系数则达到0.65.针对上述预测结果离散的问题，本文采用BP神经网络预测PEER数据库柱的屈服转角.

2 神经网络预测柱屈服转角方法

2.1 BP神经网络

BP神经网络作为前向型多层神经网络的一种，其实质是利用误差反向传播算法(Back-Propagation)对神经网络进行训练.BP神经网络结构由输入层、隐含层和输出层三个部分组成，Hornik[22]已经证明单隐层的神经网络可以实现任意精度的非线性映射关系.BP神经网络训练分为信息的正向输入和误差的反向传播两个阶段.在信息正向输入阶段，输入参数通过阀值和权值的调节，再经激活函数传递对计算结果进行输出；而在误差反向传播阶段则是通过计算输出层的结果和目标值之间的误差来反向调节各神经元的权值和阀值；在实际训练中这两个阶段交替进行，直至达到训练的性能目标为止.

但由于BP学习算法其本质是梯度下降学习算法，权值的修正是沿性能函数梯度的反向进行，使普通的BP神经网络在训练时有以下不足：1)作为一种局部搜索的方法，容易陷入局部极小值而不能得到全局最优的结果；2)由于BP算法本身反向传播的特点，使其在求解矩阵时耗费大量的计算时间，致使神经网络收敛速度很慢.针对上述不足，众多学者对其进行修正，其中L-M(Levenberg-Marquardt)[23]算法因其能够进行快速迭代，又具有全局优化的特点而在小型神经网络中得以广泛应用.L-M算法中迭代项如式(3)所示:

xk+1=xk-[JTJ+μI]-1JTe．

(3)

式中：J为雅克比矩阵；μ为调整因子；e为误差向量．当误差向量处于递减趋势时，μ的值逐渐减小；而当误差向量有反方向恶化的趋势时，μ的值将增大.L-M算法通过这种调节保证在每次迭代时都朝误差向量减小的方向进行，同时又避免因为误差一直朝递减方向发展而使迭代进入局部极小值的可能.

2.2 神经网络输入参数研究

同文献[20,24]中的分析，将柱子的屈服转角分解为如式(4)所示的三分量模型：

(4)

式中：Δy为柱子屈服位移；L为柱子计算长度；θflexural为弯曲转角分量；θslip为纵向钢筋滑移分量；θshear为剪切分量.假设柱端固定，弯矩沿柱子长度方向线性分布，弯矩曲率关系满足平截面假定，类似无裂缝柱弯矩转角关系，柱子屈服转角中的弯曲分量的大小如式(5)所示：

(5)

式中：Δflexural为弯曲位移分量；φy为柱屈服曲率；EIflexual为柱子屈服时，弯矩与曲率的比值.作为压弯构件，柱子在往复荷载作用下，截面混凝土受压区高度与轴压比，及截面配筋率相关.柱子的屈服曲率可由经验公式(6)[12]计算而得：

(6)

式中：εy为纵向钢筋的屈服应变；h为柱截面高度.将式(6)代入式(5)可得弯曲分量如式(7)所示：

(7)

式中：λ为柱剪跨比.根据上述讨论可知弯曲分量受轴压比、截面配筋率、纵向钢筋屈服强度和剪跨比影响.

对于轴压比较低的柱子钢筋的相对滑移θslip影响不可忽略[3].θslip可由式(8)[25]计算而得：

(8)

式中：fs，εs和d0分别是纵向钢筋的应力、应变和直径，fc是混凝土的抗压强度；hc是截面净高；c是截面受压区高度.分析上式可以得到柱端纵向钢筋滑移分量与纵向钢筋的应力应变状态、直径，混凝土受压区高度以及混凝土的抗压强度的平方根相关.而通过构件中力平衡关系可知混凝土受压区高度以及纵向钢筋的应力应变状态受轴压比和纵向钢筋截面配筋率控制.

以弯曲变形为主的柱，其剪切变形θshear的影响可以忽略不计，但当柱子剪跨比小于3时柱子的剪切变形开始突出.其值可以表示为：

(9)

式中：ky为形状系数；Ffirstyield与前述定义一致；Ag为柱毛截面面积；Geff为柱的有效剪切模量，可取为0.5Ec.

综合以上讨论，可以确定影响柱屈服转角的主要参数有：混凝土的抗压强度、轴压比、剪跨比、纵向钢筋的屈服强度、配筋率以及纵向钢筋直径，并将作为神经网络预测模型的输入参数.

2.3 构建BP网络预测模型

根据前述从PEER数据库中遴选出的210组数据，180组作为BP神经网络的训练集，30组作为测试集.将2.2节讨论的6个主要参数作为神经网络输入参数，柱的屈服转角为输出结果，在MATLAB中建立如图3所示的3层BP神经网络N 6-H-1(其中输入层节点数为6，H为隐含层的节点数,输出层节点数为1).

利用MATLAB神经网络工具箱建立神经网络模型需要确定以下参数：学习函数、学习速率、激活函数、训练函数、学习周期、性能目标和隐含层节点数.神经网络参数选择如下：

学习函数：Learngdm；

动量因子：0.9；

激活函数：logsig-purelin；

训练函数：L-M优化算法；

训练周期：5 000次；

性能目标：1X10-5；

学习速率：0.01；

隐含层节点数：Berry[26]认为神经网络中隐含层的节点数目为2倍的输入层的节点数，本文选择6个输入变量故而隐含层的节点数应为12.结合文献[27]中的经验公式：

N=0.5(Inputs+Outputs)+

(10)

式中：Inputs是输入层节点数，Outputs为输出层节点数，number of train patterns为训练样本个数，本文训练样本数为180,输出节点数为1，故隐含层节点数为18.根据以上讨论选择节点数为12～21.

性能函数： MSE如式(11)所示:

(11)

式中：ei为误差；ti为目标值；yi为输出值.

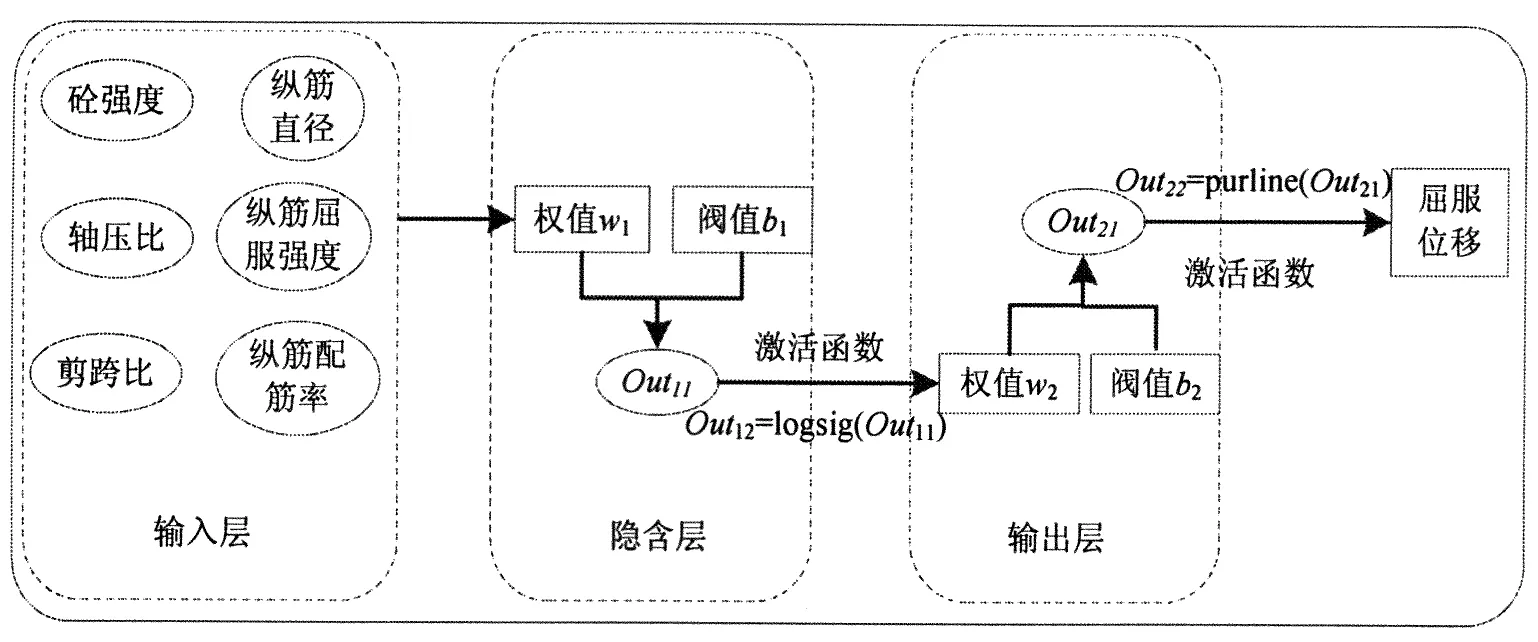
图3 混凝土柱屈服性能预测模型

利用BP网络进行预测分析，为避免因输入因子数量级差别而引起较大的网络误差,一般先将输入因子进行归一化处理.为避免激活函数其极值0和1附近饱和而伴随出现“麻痹现象”，这里采用如式(12)所示方法将神经网络的输入和输出规格化：

(12)

通过式(12)可将神经网络输入参数和输出结果的区间限制为0.1～0.9，在规格化输入参数后逐个调整神经网络参数以建立精确的神经网络预测模型.

2.4 BP网络预测结果

根据以上讨论对图3中BP神经网络进行训练、测试，得到如表2所示的预测结果．

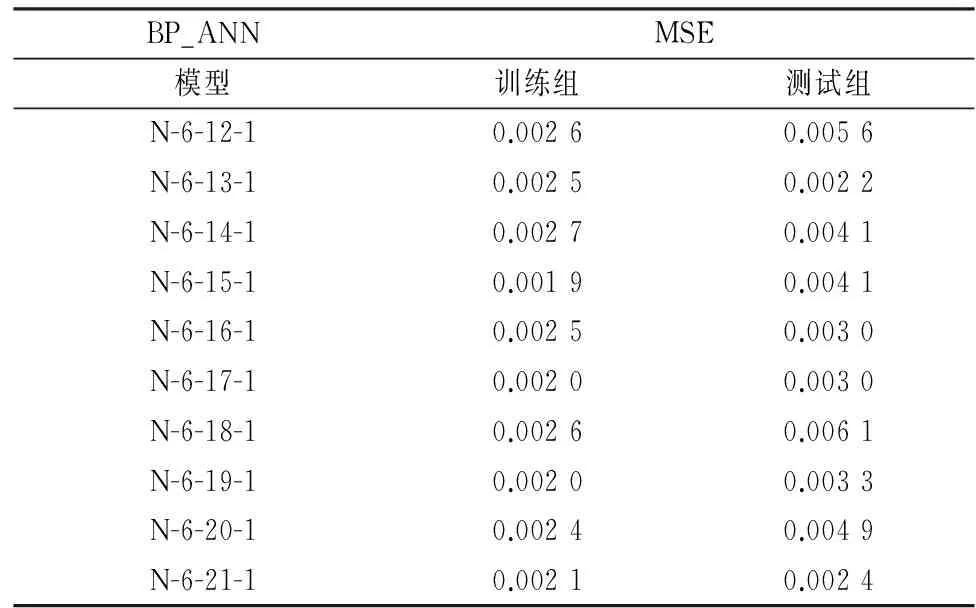
表2 不同隐含层节点数的性能函数值对比

Tab.2 Comparison of values of performance function under various hidden nodes

BP_ANNMSE模型训练组测试组N-6-12-10.00260.0056N-6-13-10.00250.0022N-6-14-10.00270.0041N-6-15-10.00190.0041N-6-16-10.00250.0030N-6-17-10.00200.0030N-6-18-10.00260.0061N-6-19-10.00200.0033N-6-20-10.00240.0049N-6-21-10.00210.0024

从表2中可以看出当隐含层节点数为13和15时，其测试集和训练集的性能函数值分别达到最小；而当隐含层节点数为17和21时，神经网络训练集和测试集的性能函数均有相对较好的取值.限于篇幅，本文只以13和15节点神经网络为例，讨论其对混凝土柱屈服性能预测的适用性.

图4和表3列出了对应节点数目为13和15的BP神经网络模型预测结果.为了进一步检验神经网络的预测能力，将这两组预测结果与实验结果进行线性回归分析，结果如图5所示.

表3 实验与BP网络预测结果对比

Tab.3 Comparison of BP network output and experimental data

BP_ANN模型预测值/实验值范围均值变异系数训练组N6-13-1[0.297,1.772]1.0010.164N6-15-1[0.441,1.434]1.0030.120测试组N6-13-1[0.730,1.396]1.0340.126N6-15-1[0.590,1.424]0.9860.179

根据表2和图5给出的预测结果以及对应的线性回归结果，其对应较小的性能函数MSE的值和较高的相关系数R的值，可以看出神经网络能够准确预测混凝土柱的屈服转角.在表3和图4中可以看出，2种不同节点数的神经网络均能取得较好的预测结果，表3中训练集和测试集的最大变异系数仅为0.164和0.179.从图4～图5以及表2～表3分析可以看到，利用BP网络预测柱的屈服位移可以得到相当满意的结果.

图4 BP网络预测结果

图5 预测模型线性回归分析

2.5 BP网络预测结果与经验模型比较

为了对比说明神经网络预测结果的准确性，本文也将Elwood在文献[20]基于理论推导的有效刚度模型带入式(2)，计算结果列于图6(a)中.同时对应式(1)中屈服位移的定义，计算对比文献[11]所提出的经验模型屈服转角：

(13)

式中：εy是纵向钢筋的屈服应变，其余符号定义和前述一致.根据式(13)计算本文数据库的屈服转角如图6(b)所示.对应13和15节神经网络预测模型、Elwood模型以及Jiang模型的统计结果列于表4.

从图6和表4中可以看出:在利用Elwood计算模型估算构件的屈服转角时，估算精度高于前述4种规范模型，但是也看出Elwood模型和Jiang经验模型估算结果依旧相当离散，其中Elwood模型计算结果变异系数较小为0.365，而Jiang模型的计算结果则为0.477.相对于上述6种经验理论模型，本文所提的13和15节点神经网络模型，其预测结果与实验值的比值均值为1；变异系数仅为0.16和0.13.

表4 BP网络预测结果与经验模型对比

Tab.4 Comparison of empirical model and BP network

模型预测值/目标值范围平均值变异系数N6-13-1[(0.114,0.20)0.29,1.94]1.0060.160N6-15-1[(0.44)0.59,1.43]1.0010.130Elwood[0.44,3.34]1.2380.365Jiang[0.36,3.46(4.75)]1.2450.477

相对于前述6种经验理论模型中仅考虑其中一部分因素的影响或者用一个数学表达式描述输入参数和柱子屈服位移之间的关系，神经网络综合考虑输入参数之间的相互影响，通过权值和阀值矩阵的调节得到更为准确的预测结果.

图6 预测模型与经验模型对比

2.6 BP网络敏感性分析

为得到输入参数对混凝土柱屈服位移的影响程度以及验证2.2节通过经验模型选用神经网络输入参数方法的合理性，本文采用基于Garson算法[28]的神经网络敏感性分析.作为基于连接权神经网络敏感性分析方法的代表，该方法通过连接权的乘积计算输入变量对输出变量的贡献程度.对于一个N X-H-1的神经网络，其计算表述如式(14)所示：

j=1,2,…,H．

(14)

式中：w1和w2分别代表输入层到隐含层和隐含层到输出层的权值.以N 6-13-1为例，进行上述敏感性分析得到如图7所示结果.

在敏感性分析中，输入参数柱屈服位移的贡献程度由敏感性系数表示.从图7中可以得到基于N 6-13-1的柱屈服位移影响的敏感性排序依次为：轴压比n0，纵向钢筋配筋率ρ0，纵向钢筋屈服强度fy，混凝土抗压强度fc，剪跨比λ，纵向钢筋直径d0.

对比图7中输入参数敏感性系数的大小，可以发现神经网络模型中每个输入参数对于柱屈服位移的影响都是不可忽略的，说明本文通过在2.2节中利用以往经验模型分析而选择的神经网络输入参数是合理的.

图7 神经网络敏感性分析结果

3 结 论

为了能够准确地预测混凝土柱构件的屈服性能，建立一种基于BP神经网络预测混凝土柱的屈服性能的方法.本文首先利用以往的经验理论模型详细解构了影响混凝土柱屈服性能的因素，并将混凝土强度、轴压比、剪跨比、纵向钢筋配筋率、纵向钢筋直径及纵向钢筋屈服强度作为BP神经网络的输入参数预测混凝土柱的屈服性能.通过与已有估算模型结果的对比，显示出利用BP神经网络预测模型的高效性.最后通过利用Garson敏感性分析方法证明了本文选择预测模型输入参数合理性，并评估了各个输入因素对混凝土柱屈服位移影响的程度.本文通过利用神经网络预测矩形混凝土柱的屈服性能，说明在数据不充分的情况下神经网络对于预测工程结果是一种很有潜力的手段.

[1] FEMA 273 Guidelines for the seismic rehabilitation of buildings[S]. Washington: Federal Emergency Management Agency, 1997:13-14.

[2] FEMA 356 Prestandard and commentary for the seismic rehabilitation of buildings [S]. Washington: Federal Emergency Management Agency, 2000:218-218.

[3] ASCE/SEI41 Seismic rehabilitation of existing buildings [S]. American Society of Civil Engineers, Reston, VA. 2007:354-354.

[4] Eurocode 8:Design of Structures for earthquake resistance Part 1: General rules, seismic actions and rules for buildings[S]. Brussels European Committee for Standardization,1998:219-219.

[5] PARK R. Ductility evaluation from laboratory and analytical testing [C]// Proceedings 9th World Conference on Earthquake Engineering．Tokyo-Kyoto, Japan. 1988：VIII,605-616.

[6] PANAGIOKOS T B, FARDIS M N. Deformations of reinforced concrete members at yielding and ultimate [J]. ACI Structural Journal, 2001, 98(2): 135-148.

[7] MONTES H E, ASCHLEIM M. Estimates of the yield curvature for design of reinforced concrete columns [J]. Magazine of Concrete Research, 2003, 55(4): 373-383.

[8] BERRY M, EBERHARD M O. Performance models for flexural damage in reinforced concrete columns [R]. Pacific Earthquake Engineering Research Center, College of Engineering, University of California， 2004:158-158.

[9] PEER. Peer structural performance database [DB/OL]. [2003-12-29]. http: // nisee. berkeley. edu / spd.

[10]钱稼茹,徐福江.钢筋混凝土柱基于位移的变形能力设计方法[J]. 建筑结构, 2007(12): 30-32．

QIAN Jia-ru, XU Fu-jiang． Displacement-based deformation capacity design of RC columns [J]. Building Structure, 2007(12): 30-32.(In Chinese)

[11]JIANG Huan-jun, LU Xi-lin, KUBO T. Damage displacement estimation of flexure-dominant RC columns[J]. Advances in Structural Engineering, 2010, 13(2): 357-368.

[12]PRIESTLEY M. Brief comments on elastic flexibility of reinforced concrete frames and significance to seismic design [J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1998,31(4): 246-259.

[14]Eurocode 8: design of structures for earthquake resistance -Part 2: Bridge[S]. Brussels European Committee for Standardization, 2005:133-133．

[15]ORETA A W, KAWASHIMA K. Neural network modeling of confined compressive strength and strain of circular concrete columns [J]. Journal of Structural Engineering, 2003, 129(4): 554-561.

[16]罗广恩,崔维成． 金属疲劳裂纹扩展速率的贝叶斯正则化BP神经网络预测[J]. 船舶力学, 2012, 16(4): 433-441.

LUO Guang-en, CUI Wei-cheng. Prediction of fatigue crack growth rate of metal based on Bayesian regularized BP neural network [J]. Journal of Ship Mechanics, 2012, 16(4): 433-441. (In Chinese)

[17]INEL M. Modeling ultimate deformation capacity of RC columns using artificial neural networks [J]. Engineering Structures, 2007, 29(3): 329-335.

[18]刘思思，赵明华，杨明辉，等. 基于自组织神经网络与遗传算法的边坡稳定性分析方法[J]. 湖南大学学报:自然科学版，2008,35(12): 7-12．

LIU Si-si, ZHAO Ming-hua, YANG Ming-hui,etal. Slope stability analysis method based on self-organizing neural network and genetic algorithm[J]. Journal of Hunan University: Natural Sciences, 2008, 35(12): 7-12. (In Chinese)

[19]王蕾，郁胜，李宾宾，等. 基于径向基神经网络的桥梁有限元模型修正[J]. 土木工程学报, 2012,45(S2): 11-15.

WANG Lei, YU Shen, LI Bin-bin,etal. Bridge model updating based on radial basis function neural network [J]. China Civil Engineering Journal, 2012,45(S2): 11-15. (In Chinese)

[20]ELWOOD K J, EBERHARD M O. Effective stiffness of reinforced concrete columns [J]. ACI Structural Journal, 2009, 106(4):483-483.

[21]ACI 318-2008 Building Code requirements for structural concrete and commentary [S]. Farmington Hills: 2008, American Concrete Institute, 2008:143-143.

[22]HORNIK K, STINCHCOMBE M, WHITE H. Multilayer feedforward networks are universal approximators [J]. Neural Networks, IEEE Transactions on, 1989, 2(5): 359-366.

[23]HAGAN M T, MENHAJ M B. Training feedforward networks with the Marquardt algorithm [J]. Neural Networks, IEEE Transactions on, 1994, 5(6): 989-993.

[24]郑罡,李贵乾. 钢筋混凝土桥墩有效刚度[J]. 土木工程学报, 2013,46(6):44-52.

ZHENG Gang, LI Gui-qian. Effective stiffness of reinforced concrete bridges piers [J]. China Civil Engineering Journal, 2013,46(6):44-52. (In Chinese)

[25]SEZEN H, MOEHLE J P. Bond-slip behavior of reinforced concrete members [C]//Proceedings of fib symposium on concrete structures in seismic regions. Athens, Greece. CEB-FIP. 2003.

[26]BERRY M J, LINOFF G. Data mining techniques: for marketing, sales, and customer support [M].New York: John Wiley & Sons Inc,1997:444-444.

[27]HAQUE M E, SUDHAKAR K V. Prediction of corrosion-fatigue behavior of DP steel through artificial neural network [J]. International Journal of Fatigue, 2001, 23(1): 1-4.

[28]GARSON G D. Interpreting neural-network connection weights[J]. AI Expert, 1991, 6(4): 46-51.

Prediction of the Yield Performance of RC Columns by Neural Network

TANG He-sheng1, 2†, LI Da-wei2, SU Yu2, ZHAO Jin-hai2

(1. State Key Laboratory of Disaster Prevention in Civil Engineering, Tongji Univ, Shanghai 200092, China;2. Research Institute of Structural Engineering and Disaster Reduction, Tongji Univ, Shanghai 200092, China)

This paper developed an artificial neural network (ANN) based method for the prediction of the yield performance of rectangular RC columns. In this method, the inputs of ANN were determined on the basis of the empirical studies of the impact factors of the yield performance of RC columns. The sensitivity analysis of the yield performance of RC columns was also investigated to validate the reasonability of the inputs selection of ANN. In order to demonstrate the feasibility and effectiveness of the proposed method, the ANN models were applied to predict the yield performance of rectangular RC columns by using 210 sets of experiment data provided by PEER, Furthermore, the predicted results were compared with empirical model results. Comparative analysis has shown that the prediction degree of agreement with the experiment results of ANN models is much better than that of other empirical prediction models. Also, the result reveals that the proposed method provides a new way for accurately estimating structural performance under earthquake with data scarcity.

rectangular reinforced concrete column; yield displacement; artificial neural network; predicted model

2014-11-28

国家自然科学基金资助项目(50708076, 51178337)，National Natural Science Foundation of China(50708076,51178337);科技部国家重点实验室基础研究项目资助(SLDRCE11-B-01,SLDRCE14-B-03)

唐和生(1973-)，男，安徽安庆人，同济大学副教授，博士

†通讯联系人，E-mail: thstj@tongji.edu.cn

1674-2974(2015)11-0017-08

TU375.3

A