一种改进的运动目标跟踪算法

江二华，王汇源

山东大学 信息科学与工程学院，济南 250100

1 引言

运动目标跟踪是指在已知的视频序列中检测目标的位置，形状以及运动轨迹等时空变化特征。在目标跟踪领域中，mean shift算法[1-4]由于简单易实现、运算速度快和鲁棒性等优点，受到广泛关注。但由于其收敛于局部极值点，故在某些背景干扰及遮挡情况下往往出现定位偏差较大甚至跟踪丢失现象。目前一般采用的解决办法包括采用粒子滤波和mean shift相结合的算法[5]、结合纹理信息的mean shift算法[6]、融合了粒子滤波和卡尔曼滤波器的跟踪算法[7]、surf和卡尔曼滤波器相结合的算法[8]等，这些算法能够达到预期的跟踪效果，但由于需要进行复杂的运算工程，使得计算效率得到影响，进而影响跟踪速度。文献[9]采用了基于角点的mean shift跟踪算法，但跟踪准确度有待提高，所以本文在文献[9]算法的基础上，提出一种融合Harris-mean shift和最小二乘法的方法，文中利用Harris-mean shift算法进行前N帧的目标搜索，根据运动目标前N帧位置信息采用最小二乘法拟合出运动轨迹，得到运动目标的预测位置，再用mean shift算法得到目标的中心位置，从而有效解决遮挡问题。

2 Harris-mean shift跟踪算法

2.1 Mean shift跟踪算法

Mean shift跟踪算法采用颜色直方图对所选择的目标区域进行建模。通过计算特征空间中每个特征值的概率来建立目标模型，目标模型的特征值u=1,2,…,m的概率密度为：

通过相似性函数的最大化，得到关于目标的mean shift向量，这个向量即是目标从初始位置向正确位置转移的向量，由于mean shift算法的收敛性，不断迭代计算mean shift向量，在当前帧中，最终会收敛到目标的真实位置（一个静止点），从而达到跟踪的目的。

2.2 Harris角点检测算法

Harris角点[10-12]对于旋转、光照、灰度、平移和噪声变化具有一定的不变性，而且仅用到灰度的一阶差分，使各个方向的变化都包含进去，所以其实时性强，定位精度较高，Harris具有算法简单、提取角点均匀合理、稳定等优点。受信号处理中自相关函数的启发，Harris算子给出与自相关函数相联系的矩阵N。自相关函数的一阶曲率是N的特征值，对图像中的任意一点，如果它的水平曲率值和垂直曲率都高于局部邻域中其他点，则认为该点是特征点。Harris算子的角点检测公式为：

其中，Iy为图像中每个像素点垂直方向上的梯度，Ix为图像中每个像素点水平方向上的梯度。在计算梯度后对矩阵进行高斯滤波，然后对式（4）进行相似对角化处理，得：

式中，α为常数，一般取0.04～0.06，本文取α=0.06。当R大于某一阈值且在某邻域内取得局部极值时，标记该点为角点（本文中阈值为0.01Rmax）。图1为Harris算子在图像区域内提取的角点。

图1 对目标和背景的Harris角点检测

2.3 融合角点的跟踪算法

Harris-mean Shift目标跟踪算法[9]，利用少量的角点作为关键点，建立目标模型和候选目标模型，增强目标与背景的可分性，从而改进mean Shift算法在复杂环境下的跟踪性能。

Harris-mean Shift目标跟踪算法步骤如下：

（1）初始化当前时刻及目标位置y0。

（2）利用Harris算法在初始的目标区域中找出目标的角点，并计算颜色直方图，建立目标模型ˆ。

（3）在以y0为中心的候选区域内利用Harris算法提取区域内的角点，计算角点的颜色直方图，建立候选模型ˆ(y)。

（5）从y0开始进行mean shift向量迭代寻找最优匹配目标，直到找到目标的真实位置y1，停止迭代。

Harris-mean Shift跟踪算法主要是使用角点特征减少了迭代次数，一定程度上提高了跟踪准确性，但跟踪实时性和准确性还可以通过改进进一步提高。

3 改进的目标跟踪算法

3.1 最小二乘法

最小二乘法[13-15]是一种数学优化技术，其目的是通过最大限度地减少偏差的平方和来寻找最佳匹配的功能，最小二乘曲线拟合方法被广泛应用于目标跟踪。

对于一组实验数据(xi,yi)(i=0,1,…,m)，需要根据这组实验数据找到自变量xi和相关变量yi之间的关系。y与x满足以下关系式：

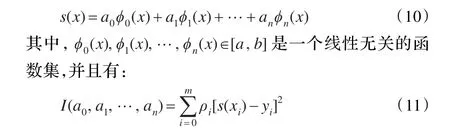
最小二乘算法的目的在于找到能使I(a0,a1,…,an)最小的最优曲线s(x)=a0φ0(x)+a1φ1(x)+… +anφn(x)，则最终曲线就是y=s(x)，如图2就是一个最小二乘算法拟合曲线的一个图示。

图2 最小二乘算法拟合曲线

在目标跟踪中，基于目标运动轨迹的连续性，用最小二乘算法计算目标的运动轨迹，然后预测目标在下一时刻的位置。

3.2 融合最小二乘法的目标跟踪

本文算法首先用Harris-mean Shift跟踪算法得到运动目标的前N个目标位置，然后以前N个目标位置为已知信息，用最小二乘算法预测运动目标的位置，然后以预测位置为搜索点，用Harris-mean Shift目标跟踪算法得到运动目标的最终位置。假设x和y分别为时间t的三次方程：

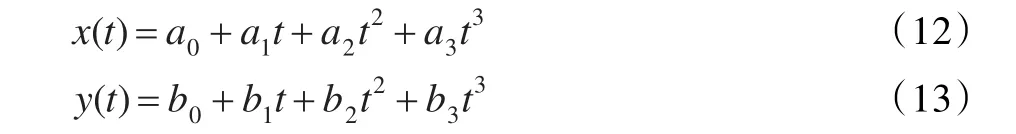
用Harris-mean Shift目标跟踪算法得到的前N帧目标中心位置作为样本点，即(xi,ti)，(yi,ti)，i=k-1,k-2,…,k-N。由公式（12）和（13）得到最终曲线方程，令t=tk，获得目标在当前帧的预测位置。把最小二乘算法的预测结果作为Harris-mean Shift目标跟踪算法的初始搜索中心，进而得到运动目标的最终位置。由于减少了初始点和收敛点之间的距离，所以相对于文献[9]跟踪算法，计算速度得到提高。本文改进算法的主要步骤如图3所示。

由文献[9]可知Harris-mean Shift算法的跟踪效果相对于传统mean shift跟踪算法已经得到较好改善，本文算法的目的只是进一步提高跟踪准确度，所以在本文算法的前N帧，采用Harris-mean Shift算法实现目标跟踪（并且N的取值一般较小，本文取值为5），即使出现偏差，该偏差也不至于影响后续步骤的跟踪效果。

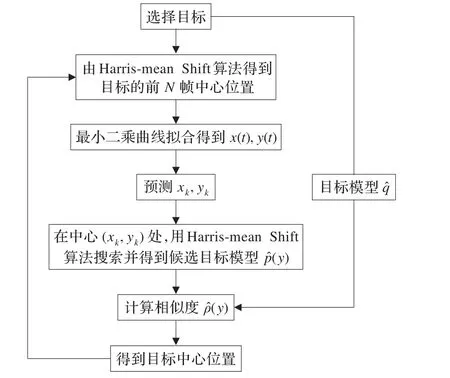
图3 改进算法的主要步骤

4 实验结果及分析

本算法在Intel i3-3110、4 GB内存的PC机上用Matlab7.0实现，实验中N=5，即采用前5帧的运动目标中心位置作为样本点。

在实验视频TEST1中，路上走的行人，其上衣颜色和背景颜色很相近，在不存在外物遮挡时，量化空间为16×16×16的RGB颜色模型下，实验结果如图4所示，图中TEST1的4帧依次是第2帧、18帧、39帧和74帧。

图4 本文算法与其他算法在TEST1视频上的比较

在图4中，本文算法和文献[9]的算法能够实现对目标的跟踪，但本文算法在目标定位上更加准确。两种算法的误差分析见表1，其中M位置和N位置分别表示文献[9]算法和本文改进算得到的目标位置，dm和dn分别表示M位置和N位置和实际位置之间的距离，由表的误差分析可知，dn小于dm，这表明本文算法的定位误差小于文献[9]算法，即本文算法的跟踪精度高于文献[9]算法，本文算法更具有可靠性，表2是本文算法和文献[9]跟踪速度的比较，可知本文算法相对于文献[9]算法跟踪速度得到了提高。

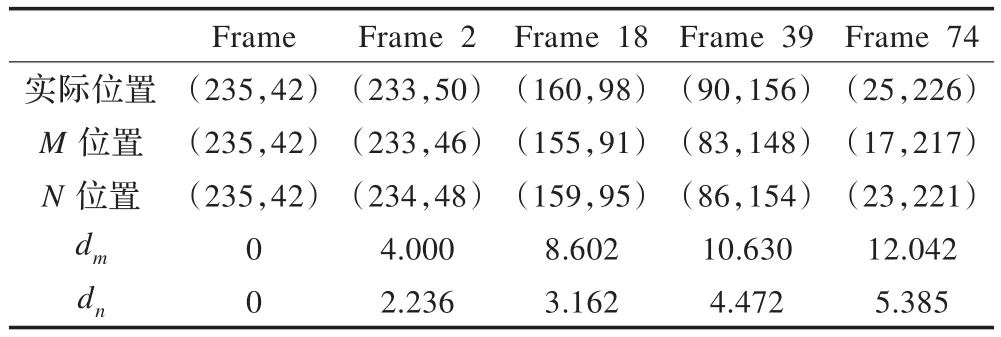
表1 本文算法和文献[9]算法的误差分析

表2 本文算法和文献[9]算法的跟踪速度比较

5 结语

新算法结合最小二乘法对Harris-mean Shift算法进行改进，改进的算法采用最小二乘法拟合曲线预测目标在下一帧的位置，改进了Harris-mean Shift算法在复杂环境下的跟踪性能，文中给出了相应的实验对Harris-mean Shift算法和改进算法做出了对比，实验表明本文算法对跟踪过程中的定位偏差问题有较强的鲁棒性。

[1]Du M T，Jie Y L.Mean-shift-based defect detection in multicrystalline dolar wafer surfaces[J].IEEE Trans on Industrial Informatics，2011，7（1）：125-135.

[2]Deilamani M J，Asli R N.Moving object tracking based on mean shift algorithe and feature fusiion[C]//Proc of the InternationalConference on ArtificialIntelligence and Signal Processing，2011：48-53.

[3]Yuan Guanglin，Xue Mogen，Han Yusheng，et al.Meanshift object tacking based on adaptive multi-features fusion[J].Journal of Computer Research and Development，2010，47（9）：1663-1671．

[4]皇甫高峻，费树岷.跟踪窗口尺度自动更新的Mean-Shift跟踪算法[J].工业控制计算机，2009，22（11）：69-71.

[5]Jiang Min，Xu Qin，Shang Tao，et a1.Tracking algorithm based on particle filtering and mean-shift[J].Computer Engineering，2010，36（5）：21-22.

[6]袁国武，徐丹.一种结合了纹理和颜色的运动目标跟踪算法[J].计算机应用与软件，2011，28（11）：81-84.

[7]Du Cbao，Liu Weining，Liu Lian.Target tracking algorithm based on kalman filter and particle filter[J].Chinese Journal of Crystals and Displays，2011，26（3）：384-389.

[8]宿德志，王坤，王玉良，等.基于SURF算法和Kalman预测的运动目标跟踪[J].海军航空工程学院学报，2013，28（4）：378-382.

[9]宁纪锋，姜光，李鹏飞.一种基于角点的Mean Shift目标跟踪算法[J].计算机应用研究，2009，26（11）：4348-4350.

[10]张小洪，李博，杨丹.一种新的Harris多尺度角点检测[J].电子与信息学报，2007，29（7）：1735-1738.

[11]Loog M，Lauze F.The Inprobability of Harrris interest points[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2010，32（6）：1141-1147.

[12]卢瑜，郝兴文，王永俊.Moravec和Harris角点检测方法比较研究[J].计算机技术与发展，2011，21（6）：95-97.

[13]王可，毛志.基于Matlab实现最小二乘法曲线拟合[J].自然科学报，2005，12（2）：52-56.

[14]张起贵，张魁.基于最小二乘直线拟合的小目标检测[J].电子设计工程，2010，18（7）：176-180.

[15]徐瑜，杨绍清，孙牧.最小二乘滤波在目标跟踪中的应用[J].指挥控制与仿真，2007，29（4）：41-42.