基于混沌映射的HMAC算法设计与分析

李慧佳，龙 敏

长沙理工大学 计算机与通信工程学院，长沙 410114

1 引言

消息认证码（Message Authentication Code，MAC）是保证数据完整性的基本算法，被广泛应用于金融、商业系统等各种安全系统中。MAC算法能够避免攻击者通过伪造、重放、篡改、乱序等手段来改变数据，而且能验证报文发送者和接收者的真实性以及报文的完整性。目前，有多种用于构造MAC算法的方法，除了基于分组密码设计的CBC-MAC、TBC-MAC、XOR-MAC外，采用带密钥的散列函数也常用于设计MAC，其中具有代表性的是M.Bellare等人于1996年提出的HMAC算法[1]，被广泛使用于各种网络协议以及身份认证系统中，并已经取代RFC1828成为了IPSec协议中的认证算法[2]。

一直以来，散列函数是现代密码学中重要的组成部分，优良的单向性能使得它在保密通信中倍受青睐，是确保许多密码协议和密码算法安全的前提条件。然而，在2004年美密会上，我国的学者王小云等宣布了经典散列函数MD4、MD5、SHA-1的成功“碰撞”[3]，由它们构造的HMAC算法也被证实存在伪造攻击和部分密钥恢复攻击[4]的可能性；基于39步SHA-256函数的LPMAC算法以及秘密前缀MAC算法也因为能够成功找到特殊

CNKI网络优先出版：2014-04-01,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0176.html的差分路线使得SHA-256算法出现了碰撞[5]证实基于SHA-256的MAC算法易遭受区分攻击。

除了上述基于传统散列函数的HMAC算法外，还存在不同hash种类形式的HMAC算法，如基于三维Rossler系统的增强型HMAC[6]、采用SHA256与HMAC相结合的优化方案[7]等等，这些算法采用结构不一的压缩函数，外加一系列简单的逻辑运算及数学运算来获得最终的MAC值。然而由于压缩函数的构造不严谨以及部分细节处理不当，HMAC算法仍旧存在被攻破的可能。如文献[8]中，作者针对一种块分组结构的hash函数作出安全性分析，由于该压缩函数在生日攻击下仅需要216.5计算复杂度就能够找到一个碰撞对，使得输出的MAC值相同，攻击者可以通过密钥恢复攻击或者区分攻击来获得其想要的认证消息。

因此，用于构造HMAC的单向Hash函数的安全性至关重要，本文将融入混沌映射设计单向Hash函数，以提高HMAC算法的防伪造攻击能力。

2HMAC算法及攻击分析

2.1HMAC算法描述

HMAC是消息和密钥的公开hash函数，它要求所使用的hash函数具备迭代结构，反复使用压缩函数将任意长度的消息映射为定长的短消息。设h是嵌入的hash函数，m是输入HMAC的消息，b是消息m分块后每一块的比特长度，K是密钥，若长度小于b则在K末尾用0填充至b比特长，记为K+；若K长度大于b则K+=h(K)，ipad和opad是HMAC两个固定的长度为b的参数，分别是x36、x5C（十六进制）重复b/8的结果，HMAC算法描述如下[9]：

HMACk(m)=h(IV,(K+⊕opad)||h(IV,(K+ipad)||m))（1）

HMAC算法的构造流程图如图1所示。

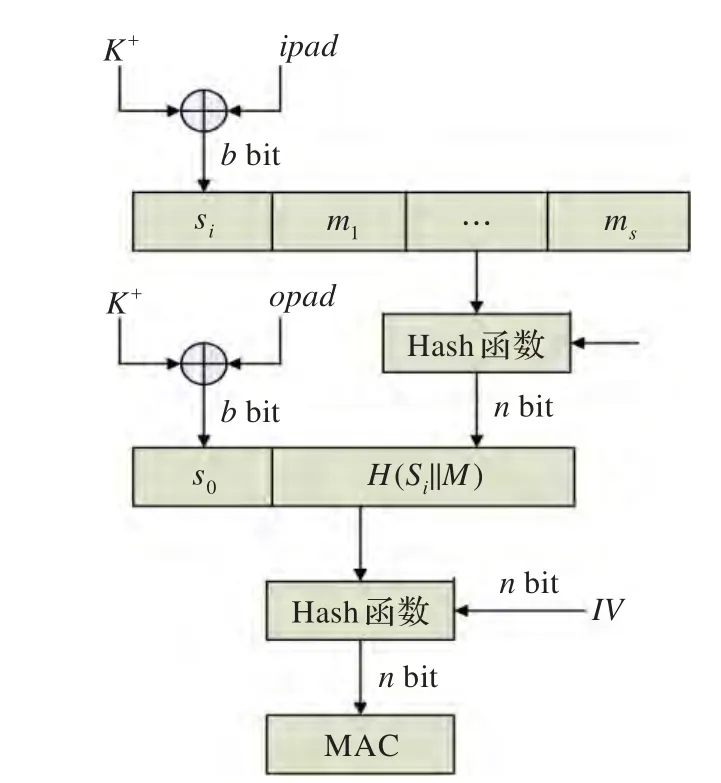
图1HMAC算法流程图

其中IV是hash迭代函数的固定初始值，n为hash函数输出的hash值长度。HMAC算法步骤阐述如下：

步骤1在字长为b的密钥K+与ipad做异或运算，并将结果字符串填充于消息m的数据流中。

步骤2用hash函数作用于上一步生成的数据流。

步骤3将密钥K+再与opad做异或运算，结果填充至第一轮hash后的比特流中。

步骤4再调用hash函数作用于上一步的比特流，输出最终的MAC值。

概括来说，HMAC算法是由一组固定参数与明文消息m经简单处理（填充、异或）后在压缩函数F的多轮迭代作用下生成MAC值。据此HMAC算法结构还可以迭代状如图2展现出来。

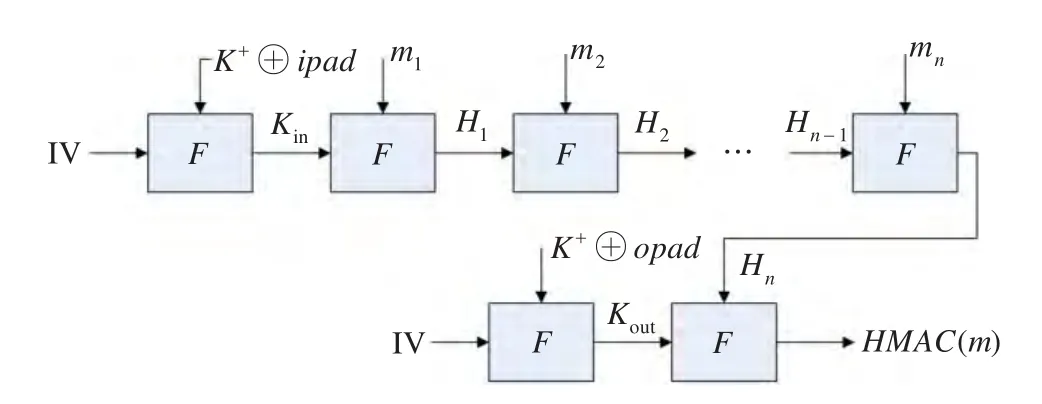
图2HMAC的迭代状结构

图中，压缩函数F在处理明文时是分块独立进行压缩处理，故hash函数的初始向量IV、固定参数ipad、opad可看作压缩函数F进行第一轮压缩处理的输入值，即Kin=F(IV,K+⊕ipad)，Kout=F(IV,K+⊕opad)。

2.2 攻击实例及原因分析

攻击实例：由于各参数未知且固定，明文消息是公开的，从Kin，Kout计算式子可知，Kin和Kout的值虽是未知但却是固定的，因而第一轮hash后输出的值是一固定常数，显然在处理消息明文块时其链接变量是通过hash一个固定常数而得，攻击者可以利用这一固定常数伪造一个新消息的MAC值并且通过合法验证。假设攻击者通过随机选择消息得到消息M1=m1‖m2‖m3…‖mn，M2=m′1‖m′2‖m′3…‖m′n，并且获得两者的MAC值满足相等关系，即H1=HMAC(Kin,Kout,M1)=HMAC(Kin,Kout,M2)=H2；攻击者再获得一组消息M3=m1‖m2‖…‖mn‖mn+1‖…‖mr的MAC值为H3=HMAC(Kin,Kout,M3)，则攻击者可以成功伪造消息值也为H3，其中n、r都为正整数。

攻击原因分析：由于HMAC算法中密钥K未知且固定，固定参数ipad、opad为两个不相等的常数，在压缩迭代处理不同明文消息块的情况下，使用的初始向量及常态参数相同，且Kin和Kout值不变，则易发生上述存在性伪造攻击。此外，上述攻击实例是基于找到两个不同消息的MAC值相同的假设条件下进行验证的，而根据生日攻击原理[10]，找到一对消息M≠M′满足MAC(M)=MAC(M′)所需要的计算复杂度大约为其中n为MAC值的长度，即上述攻击实例能够成功实施攻击需要的计算复杂度约为，这个数值远低于带密钥hash函数的安全攻击复杂度下限O(2n)，故而上述的假设条件是成立的。

3 一种基于混沌映射HMAC算法的构造

3.1 随机序列发生器的构造

算法使用Logistic映射和Chebyshev映射两个混沌系统构造随机序列发生器。Logistic映射定义为[11]：

当xn∈(0,1)，r∈(3.569 9…,4]时，系统处于混沌状态。Chebyshev映射定义为[12]：

其中yn∈[-1,1]，k为Chebyshev映射的阶数，当k＞2时李雅普诺夫指数λ=lnk＞0，即系统处于混沌状态。

为了抵御伪造消息等攻击，本文采用一个混沌序列发生器来动态生成HMAC算法中的参数ipad和opad，在处理不同的消息时，使得用户使用的参数也不同，从而防止攻击者采用相等MAC值的两组消息试图伪造新消息来获得验证的通过。该混沌序列发生器由四部分组成：逻辑函数G、Logistic映射、Chebyshev映射以及线性反馈移位寄存器。其总体结构如图3所示。

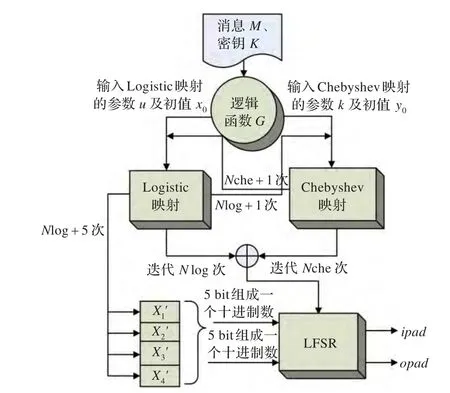
图3 混沌序列发生器的构成

图中，明文消息和密钥分别经过由一系列逻辑运算组成的逻辑函数G处理之后左右输出两组实数{μ,x0}、{k,y0}，分别作为混沌映射的控制参数以及迭代初始值；两组数据分别驱动混沌映射进行迭代，并将迭代次数加1次后的值反馈到下一轮迭代开始前，与相应的参数做关联处理后再进行迭代操作；同时分别输出两组混沌映射的末尾4组迭代值，两者异或后作为线性移位反馈寄存器的初始状态值；此外再获得Logistic映射的迭代次数加1~5次的4组迭代值（共128 bit），从中分别抽取两组5bit二进制并转换成两个十进制数，作为LFSR的移位控制参数来控制初始序列的循环移位；LFSR经过两路循环移位后输出两组128 bit序列，即为HMAC参数ipad和opad的值。

逻辑函数G是一组由循环移位、按位异或、取反、按位与、或等操作混合运算实现的扩散机制。它能够有效将明文消息块变化数最大可能扩散影响，使得明文初始条件产生微小变化的情况下引发该状态变量内部的动态强差分扩散，增强混沌序列发生器初值敏感性能。逻辑函数G的构造如图4所示。

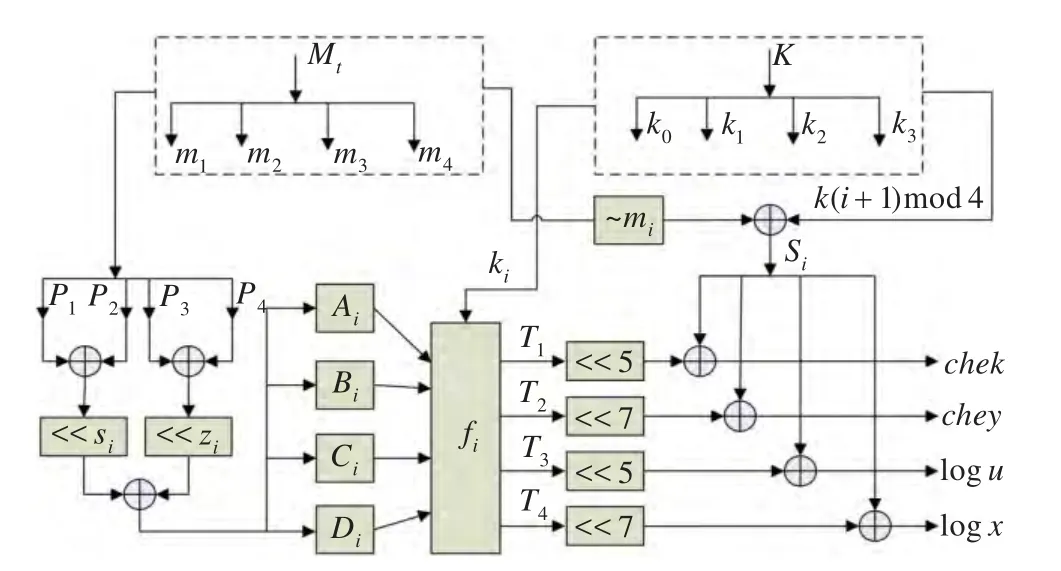
图4 逻辑函数G的结构

将一组明文消息块Mt按照一定方式进行分组后(P1,P2,P3,P4)两两异或再分别进行四次循环移位，其中si=(i+14)mod4+5*i，zi=(i+12)mod4+6*i，且i=1,2,3,4；再次异或后每组128 bit分组输出四轮32 bit的序列（Ai,Bi,Ci,Di），输入fi函数中结合密钥K进行逻辑操作的混合运算。fi函数表述如下：

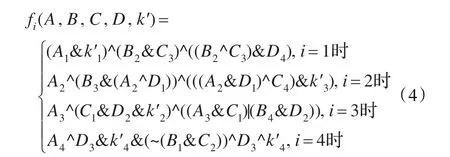
混合运算后，fi函数的四组输出再经移位、异或等处理后分别输出四组数据，即为两个混沌映射的控制参数初值和初始迭代初值。

3.2 基于混沌映射的HMAC算法描述

本文所设计的HMAC算法采用上述随机序列发生器来将明文消息转化成为定长的数据流，通过一系列逻辑运算与混沌映射相结合达到消息扩散最大化，明文消息与数据流产生不可逆转的关联以防止攻击者有可乘之机。本文提出的HMAC算法参数生成步骤描述如下：

步骤1消息分块与填充。将任意长度的明文消息M分割成128 bit的消息块M1,…,Mi…,Ms，并将消息长度嵌入到填充消息中，消息长度为128 bit的整数倍，填充后的消息形式表示为M′=100…length(M)M10…0。

步骤3混沌迭代。将上一步骤获得的各个参数值对应输入两个混沌映射中进行迭代，取x0，y0数值的低十位和低十五位数字组成两个十进制数I,J，迭代次数定义为：N=230+(IorJ)+i，i为消息块数目。

步骤4截取和移位。消息块迭代N次后，输出两个映射迭代值的最末尾四个数，截取两串128 bit二进制流，逐位异或后获得线性移位反馈寄存器的初始状态值SIV；取两映射的N+1次迭代值反馈到下一轮消息块处理，并与原混沌映射初始值相乘获得新初始值继续参与下一轮迭代。

步骤5重复混沌迭代过程直到处理完最后一组消息块，最后从N+2~N+5次logistic映射迭代开始输出系统当前4个值X′1,X′2,…,X′4，截取128 bit二进制序列后从中抽取出10位组成两个十进制数（每5位一个数）Or，Oe作为控制LFSR的初始状态值SIV循环移位的比特数，最终获得两串移位后的128 bit序列，即分别为HMAC参数ipad和opad的序列值。

3.3 算法性能分析

3.3.1 初值敏感性分析

原有的HMAC算法由于其内在参数的固定存在被攻破的风险，本文提出的改进算法采用了相关混沌理论生成动态可变的参数为HMAC算法提供了安全保障。由于HMAC应用时明文消息与最终认证码是公开的，攻击者一般通过大量观察和统计两者之间存在的关联来施以攻击手段，若明文消息的微小变化能够引起认证码翻天覆地的改变，则攻击者无的放矢，无疑能够保证认证的安全性。

取一段初始明文文本1“Cryptography is the study of mathematical techniques related to aspects of information security such asconfidentiality，data integrity，entity authentication，and data origin authentication，and data origin authentication.”做仿真实验，设密钥（十六进制表示）K="FC50ADB815BF2C00ADF379EEA046BC2E"，以明文文本1和密钥混合扩散后映射到混沌的参数空间，经过混沌序列发生器后获得两串128 bit二进制流。

改变初始明文文本，使得文本发生微小变化以测试混沌系统的初值敏感性能，采用下述几种情况来测试系统结果：

情况1：将文本1的首字母C改为B；

情况2：将文本1中的data origin改为data origim；

情况3：将文本1中entity authentication改为entity authentications；

情况4：删除文本1中最后一个字符“.”；

情况5：将密钥K的首字符F改为E；

将各个改变后的文本逐个经过混沌序列发生器后生成序列结果如下所示（用十六进制表示）。

理想状态下的混沌加密函数在初值的微小扰动情况下产生的结果能够以每比特50%的概率产生变化。与初始文本1的ipad和opad值相比，上述五种不同条件下生成ipad和opad结果的变化比特数分别为：（61，61）、（64，68）、（63，65）、（65，63）、（74，68），每一个变化比特数都接近于128-bit的50%，这说明混沌序列发生器对初值的变化非常敏感，混沌映射的初值敏感特性得到了充分的体现。

3.3.2 统计性能分析

本文提出的HMAC算法以混沌映射方式生成HMAC的参数，整个过程可看作是一次数据加密过程，文献[13]提出采用混乱与扩散两个标准来衡量一个加密算法的安全性能，加密体制中要求明文在密文空间中呈现充分的扩散与混乱，明文一比特变化须尽可能影响密文空间的所有比特位。混乱与扩散性能分析可通过以下几组定义来实现：

定义P的均方差为：

测试方法：随机选取一段明文进行加密，得到相应的结果序列，然后改变明文1 bit的值进行加密得到另一个序列结果，比较两个结果得到变化比特数Bi。令测试次数N=256,512,1 024,2 048,4 096，测试结果如表1所示，图5为N=4 096时结果序列的置乱数分布情况。图中，平均变化比特数-B和平均变化概率P都趋近于理想状况下的64 bit和50%，4096次测试的变化比特数介于40到83之间，波动较小。因此，基于混沌映射的HMAC算法能够产生对初值非常敏感的动态参数值，且保障了参数选取所属的参数空间值充分均匀，均方差ΔB和ΔP都很小，保证了混乱与扩散程度聚集在一个平均稳定的水平上。

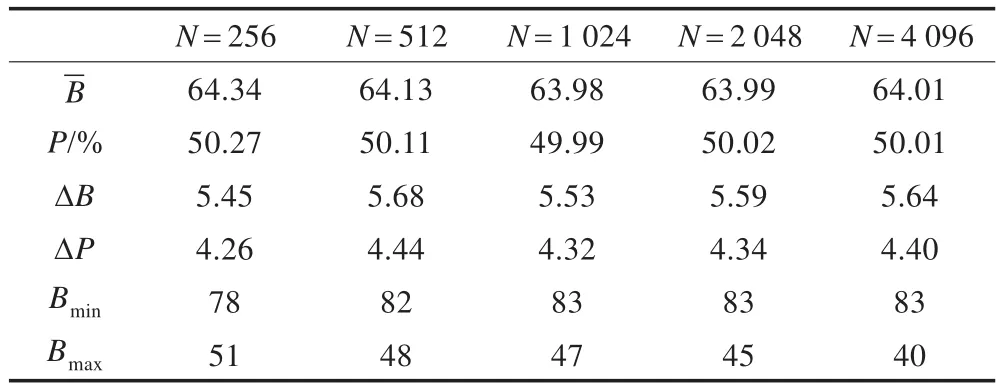
表1 基于混沌映射HMAC算法的统计性能分析

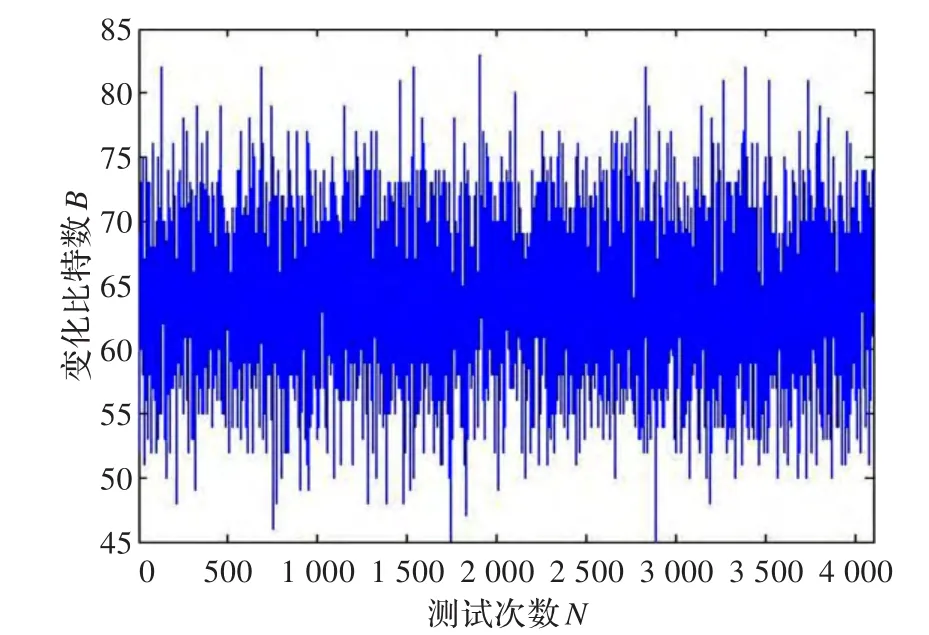
图5 测试次数为4 096的置乱分布图

3.3.3 抗碰撞性能分析

HMAC算法属于一种基于带密钥的hash函数，其安全性高度依赖于hash函数的安全性，而hash函数潜在的可能性安全隐患一般在于hash函数内部出现碰撞。本文通过统计相同位置上hash值对应的ASCII值相同的数目分布来测试HMAC改进算法的抗碰撞性能（如图6所示）。

针对本文的改进算法采用以下实验来定量测试其抗碰撞能力：随机选取一段明文生成128比特ipad和opad结果，用ASCII码的形式存储；然后随机选择改变该明文中1 bit的值得到另一组新的结果，比较两组结果，统计在相同位置上ASCII码值相同的数的情况。以ipad结果为例，经过4 096次测试，相同位置上出现相同ASCII码值的碰撞次数如图6所示。由图可知，在4 096次测试中，3 850次没有发生碰撞，240次发生了一次碰撞，仅仅6次发生了二次碰撞，碰撞程度非常低，攻击者找到碰撞对的概率微乎其微。

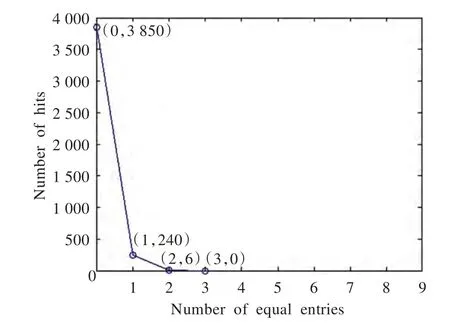
图6 相同位置ASCII值相同的数目分布

3.3.4 抗存在性伪造攻击分析

4HMAC的安全性要求

HMAC算法主要由密钥与hash函数相结合而成，即修正了迭代hash函数固有缺陷，也充分考虑到了不同攻击模型的攻击代价；由于离线攻击比在线攻击更易于完成，在构造HMAC时特别在二次hash运算中使用密钥，以此加强对离线攻击的抵御能力。尽管如此，HMAC安全性除了高度依赖于参数ipad和opad的取值以外，还与嵌入的hash函数安全性以及密钥的安全性相关联。

目前针对HMAC算法提出的攻击实例基本都是由于嵌入的hash函数内部结构发生碰撞而导致的[7-8，11]，其主要攻击方式为碰撞攻击，攻击强度取决于hash函数的hash值以及密钥的长度。文献[14]指出，消息的散列值长度n应不小于128比特，使得找到一对消息m≠m′满足h(m)=h(m′)所需要的计算复杂度约为，可以防止生日攻击。对于任意一种MAC算法，存在一个无可避免的缺陷，即算法认证过程中，即使在密钥未知的情况下，通过随机选择消息反复测试，总能找到一个明文消息对应的伪MAC值，并能通过验证，其中找到该伪MAC值的概率为(1/2)n[15]。因此在HMAC算法中，若要对hash函数输出值进行截短处理，则截取的MAC值长度应不小于hash输出值长度的一半，以此来减小MAC算法自身不足带来的危害。

除此之外，恢复密钥也是攻击HMAC算法的主要手段。由于密钥是私有的，在不考虑持有方泄露的情况下，密钥的安全性依赖于密钥的长度和随机性。对于长度为K比特的密钥，实施强力攻击需要2K次操作即可恢复密钥，在现有计算机计算强度前提下，为了防止密钥穷尽搜索攻击，要求密钥的长度不能小于128比特，且不小于hash函数输出值的长度，而大于hash值长度的密钥虽然可以使用，但额外的长度并不能显著提高HMAC算法的安全性，因此推荐使用密钥长度等于hash值长度的密钥[15]。此外，密钥起源函数必须是伪随机的，并且要周期性的更新，以此保证密钥的安全性。

除上述分析以外，要确保HMAC算法的安全性还须满足以下几个基本要求：如（1）hash函数须满足本身几点特性，如单向性、弱抗碰撞性以及良好的雪崩效应等；（2）hash散列值呈均匀分布，以抵御统计分析；（3）攻击者已知消息m和MAC值C(m)情况下，构造满足C(m1)=C(m)的消息m1在计算上不可行。

5 结束语

HMAC算法在消息认证方面有着重要而广泛的应用，本文在提出该算法存在固有缺陷的基础上，分析了该缺陷致使HMAC存在存在性伪造攻击，并予以实例证明；同时提出一种基于混沌映射的HMAC算法方案，该方案采用混沌Logistic映射和Chebyshev映射相结合组成一个混沌序列发生器，通过循环移位、逻辑异或、取反等来完成拉伸和折叠操作，实现了消息明文生成HMAC动态参数的目的。实验与分析结果表明，本文的改进方案有着良好的混乱与扩散性能，且碰撞程度非常低，消息明文的微小改变能产生极为不同的参数结果，故采用此方案来动态生成HMAC算法的固定参数ipad和opad能够有效防御因HMAC算法的参数ipad和opad是常态参数而造成的伪造攻击。最后针对目前HMAC算法构造存在的攻击模式提出了安全性要求，及其嵌入的hash函数需满足的安全性条件。

[1]Bellare M，Canetti R，Krawczyk H.Keying hash function for message authentication[J].Advances in Cryptology，1996，1109：1-15.

[2]Khan E，EI-Kharashi M W，Gebali F，et al.Design and performance analysis of a unified，reconfigurable HMACHash unit[J].IEEE Trans，2007，45（12）：2683-2695.

[3]Wang X Y，Feng D G，Lai X J，et al.Collisions for hash functions MD4，MD5，HAVAL-128，and RIPEMD[C]//Advances in Cryptology-CRYPTO 2004；The 24rd Annual International Cryptology Conference.Berlin：Springer-Verlag，2004.

[4]Contini S，Yin Yiqun Lisa.Forgery and partial key-recovery attacks on HMAC and NMAC using Hash collisions[J].ASIACRYPT 2006，LNCS 4284，2006：37-53.

[5]Yu Hongbo，Wang Xiaoyun.Distinguishing attack on the secret-prefix MAC based on the 39-Step SHA-256[C]//ACISP 2009.Berlin Heidelberg：Springer-Verlag，2009，5594：185-201.

[6]Idris S，Zorkta H，Khawatmi S，et al.Enhanced HMAC based upon 3-D rossler system[J].IEEE Computer Society，2009.

[7]须磊.HMAC-SHA256算法的优化设计[J].价值工程，2012，29（2）：202-204.

[8]Yuan Zheng，Ren Xiaoqiu，Liu Jintao.Distinguishing attacks on MAC/HMAC based on a new dedicated compression function framework[J].International Association for Cryptologic Research，2010：2-5.

[9]于广威，何文才.基于HMAC的加密狗设计[J].信息安全与通信保密，2011，11（3）：68-72.

[10]郑世慧，张国艳，杨义先，等.基于混沌的带密钥散列函数安全分析[J].通信学报，2011，32（5）：146-152.

[11]李进，徐红.基于MD5算法和Logistic映射的图像加密方法研究[J].信息网络安全，2011，8（9）：25-47.

[12]邓绍红，黄桂超，陈志建，等.基于混沌映射的自适应图像加密算法[J].计算机应用，2011，31（6）：1502-1511.

[13]Kanso A，Yahyaoui H，Almulla M.Keyed hash function based on a map[J].Information Sciences，2012，186（2）：249-264.

[14]Bakhtiari S，Safavi-Naini R，Pieprzyk J.Keyed Hash Functions[R].Department of Computer Science，University of Wollongong，NSW 2522.

[15]Evans D L，Bond P J，Bement A L.The keyed-Hash message authentication Code（HMAC）[J].Federal Information Processing Standards Publication，2002.