晋江滨海新区护岸越浪量试验
陈佳琪, 陈国平 , 高晨晨, 严士常
(河海大学 港口海岸与近海工程学院,江苏 南京210098)
越浪量是指波浪越过沿海建筑物(海堤或护岸等)的水量,通常以平均越浪量表示。越浪量的大小直接关系到堤体和堤后结构的稳定安全。目前国内外对越浪量的研究主要集中在直立式海堤和斜坡式海堤两方面。在对直立式海堤堤顶平均越浪量的研究方面,合田良实方法被广泛采用[1]。该方法根据不规则波模型试验及越浪计算成果绘制了越浪量推算表,通过查表可得不同情况下直立式海堤堤顶越浪量。在对斜坡式海堤堤顶平均越浪量的研究方面,Van der Meer[2]研究了前坡平均坡度、堤前地形及水深变化、平台宽度及高程、波浪斜向入射角等对越浪量的影响,其越浪量计算公式被欧洲许多国家推荐使用。我国《海港水文规范》[3]详细列举了斜坡堤有无胸墙时,护面结构型式、建筑物前水深、坡度及有效波高等波要素对越浪量的影响。陈国平等[4-5],以波浪爬高、墙顶超高为2 个主要影响因子,综合考虑挡浪墙墙顶超高、波要素、平台结构型式对越浪的影响,大大简化了越浪量计算公式。
影响越浪量的因素很多[6-12],主要有海堤的结构型式、海堤堤脚处水深、堤前入射波要素等。其中波向角(θ)为堤前入射波要素中的主要影响因素。在θ 对越浪量的影响研究方面,Owen[13-14]认为光滑斜坡堤上单向波的越浪量在θ <30° 时基本不变或可能出现比正向入射时更大的值即所谓“小角度斜向增加”。Franco L[15]考察了单向波中θ 对越浪量的影响,指出θ <50°时,随着θ 的增大,越浪量明显减小;θ ≥50° 时,随着θ 的增大,越浪量基本不变。Franco L[16]还指出在多向波的情况下,θ 对越浪量的影响有着非常大的不同。θ <20° 时,随着θ 的增加越浪量基本不变化;θ ≥20° 时,随着θ 的增大越浪量逐渐减小。
由于影响越浪因素的复杂性及各研究者所选取的海堤断面结构型式不同,每个经验公式都有其使用条件。并且关于θ 对越浪量的影响研究资料较少。因此继续开展越浪量问题的研究仍然很有必要。
1 物理模型简介
晋江滨海新区填海造地工程陆域形成范围总面积约为42.14 km2,建设外侧护岸长17.62 km、内侧护岸长45.31 km,外侧护岸呈缓S 状曲线分布,外侧护岸东段、中段、西段不同区段所承受的控制浪向亦不同。尤其是K2~K3段,结构设计采用SSE 向波浪,入射波向与堤轴线几乎平行。
试验在河海大学多向不规则波港池中进行。水槽长60.0 m,宽40.0 m,高1.2 m,港池一端安装不规则造波机,另一端设置消波系统,港池四周设置消浪格栅。试验采用不规则波,波谱为Jonswap 谱。
晋江滨海新区护岸结构如图1 所示。

图1 晋江滨海新区护岸结构示意Fig.1 Diagram of Jinjiang Binhai coast revetment structure
由图1 可以看出,试验中采用复合式断面,护岸采用袋装沙作为堤心,堤顶高程为6.25 m,铺设0.55 m 厚路面,后坡采用0.40 m 厚的干砌块石护面。直立式防浪墙顶高程为7.00 m,防浪墙前随机摆放2 排3T 扭王块体,呈全掩护形式。在3.95 m 高程处设置长度为10.00 m 的二级平台,平台上下坡坡度均为1 ∶2,采用随机摆放3T 扭王块体护面,两层单个质量200 ~300 kg 的块石作为垫层,在0.06 m高程处采用单个质量300 ~500 kg 的块石作为压脚块石,- 1.39 m 高程处也采用单个质量200 ~300 kg 的块石护底,长度为6.80 m。试验波浪要素见表1。

表1 试验波浪要素Tab.1 Elements of waves
2 试验结果及分析
2.1 外护岸前沿相对波高分布
波浪点位布置如图2 所示。在原始地形情况下,取土区已经开挖,护岸工程未建。分别测量:100 年一遇潮位、100 年一遇波高下,SSE 波向、S 波向以及设计高潮位、100 年一遇波高下,SSE 波向、S 波向组合情况下的波浪要素分布。相对波高(Hc/Hs)分布如图3 所示。
由图3 可以看出,SSE 向波浪作用下,K2~K4段沿堤轴线由东向西相对波高逐渐增大。但K1~K2段SSE 向相对波高沿程略有减小趋势,主要受局部地形及取土区开挖影响,折射波浪与入射波叠加引起。S 向波浪作用下,沿堤轴线由东向西相对波高逐步增大。
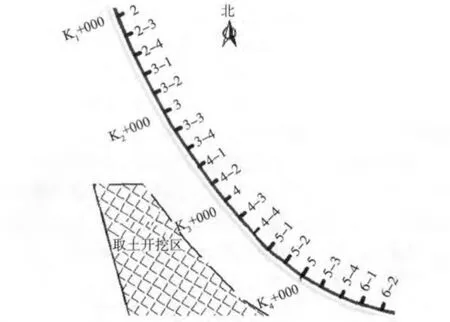
图2 护岸前沿波浪点位布置Fig.2 Wave height of the measurement location on revetment

图3 护岸前沿相对波高分布Fig.3 Distribution of the relative wave height on revetment frontier
2.2 波向角对相对越浪量的影响
在100 年一遇潮位及相应SSE 向波浪组合下,分别取西北护岸K1~K2,K2~K3,K3~K4之间堤段为主要研究对象,采用K2,K3,K4点波浪要素作为代表波浪。护岸后方中部各设置8 个集水槽用以收集越浪,集水槽布置如图4 和图5 所示。护岸断面见图1,护岸前沿相对波高分布见图3。
图6、图7 分别为100 年一遇潮位及相应SSE 波向下,K2~K3,K3~K4堤段护岸前沿θ 与无因次越浪量(Q/(gHs3)0.5)之间的关系。
末次随访时,按照Johner-Wruhs评定标准评定临床疗效见表5。优良率UTN组85.19%,LCP组81.82%,UEF组67.74%。一期采用锁定钢板内固定治疗典型病例见图1。
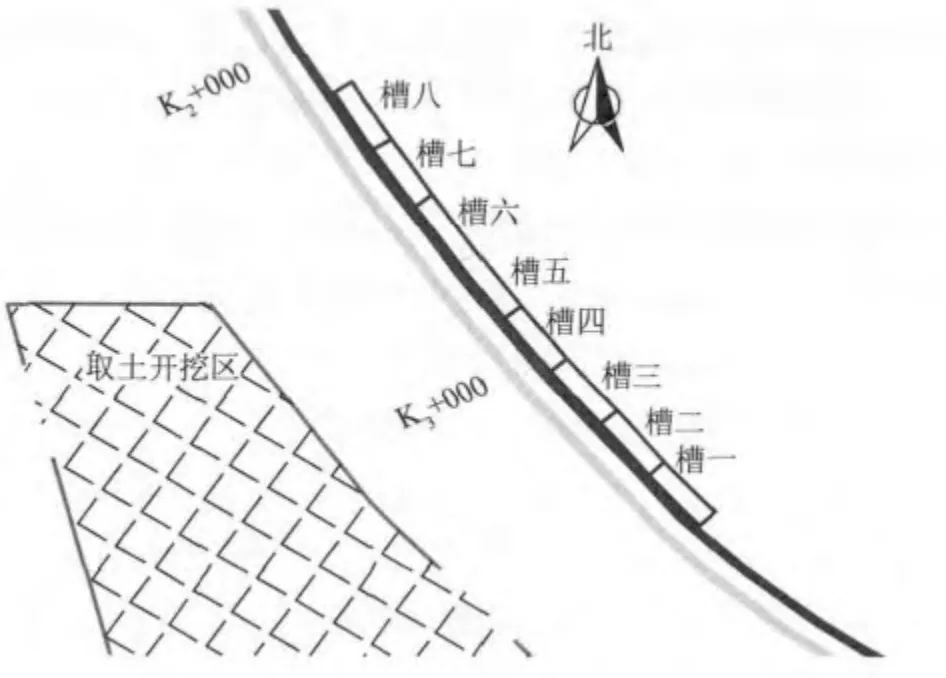
图4 K2 ~K3 堤段槽位布置Fig.4 Measuring location for K2 ~K3
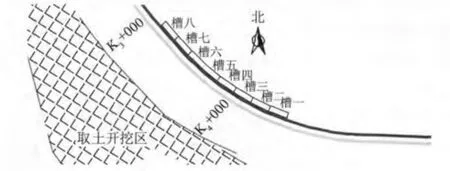
图5 K3 ~K4 堤段槽位布置Fig.5 Measuring location for K3 ~K4

图6 K2 ~K3 堤段护岸前沿相对越浪量分布Fig.6 Distribution of the relative overtopping on K2 ~K3 revetment frontier

图7 K3 ~K4 堤段护岸前沿相对越浪量分布Fig.7 Distribution of the relative overtopping on K3 ~K4 revetment frontier
由图6 可以看出,当防浪墙墙顶超高Hc/Hs<1.0,20° ≤θ <40° 时,由东向西(槽一~槽八)随着波向角的增大越浪量明显减小。θ >40° 时,由东向西(槽一~槽八)随着波向角的增大越浪量先增大,后减小,当θ = 50° 左右时,越浪量达最大值。
2.3 波浪斜向入射对越浪量的影响
分别取西北护岸K1~K2,K2~K3,K3~K4之间堤段为主要研究对象,在100 年一遇潮位及波浪正向入射下,实验段堤轴线与来波方向垂直。护岸后方中部设置3 个集水槽用以收集越浪,集水槽布置见图4、图5。护岸断面见图1。
K1~K2,K2~K3,K3~K4堤段,在4.63 m 潮经,10.1 s 平均周期,波浪正向入射与斜向入射下越浪量对比结果见表2。

表2 波浪正向入射与斜向入射下越浪量对比Tab.2 Contrast of overtopping between the forward and oblique incident wave
由表2 可以看出,由于波浪斜向入射,波向和堤轴线夹角较小,相当于作用在护岸上的能量流减小,并且斜向入射波浪在平台上传播距离加长,相当于平台加宽,波浪在平台上破碎,消耗大量的能量。因此与波浪正向入射试验结果相比,波浪斜向入射时平均越浪量比正向入射时约小一个数量级,有的甚至小二个数量级。
2.4 波向角对越浪量的影响
外护岸前沿取土区开挖,局部地形的改变,会引起波浪折射,波浪传播时波向发生改变。根据波浪数学模型计算结果(见表3),高水位时,SSE 向波浪往S 偏转约10°左右。由于受波浪局部整体物理模型模拟范围的限制,模型中波向偏转较小。
为了论证波向偏转对平均越浪量的影响,文中将SSE 向入射波往S 向偏转11.25°,进行K2~K3之间堤段越浪量试验。模型布置、试验方法同K2~K3堤段。

表3 入射波向与模型范围内各计算点位波向角Tab.3 Wave direction of the calculated point within the model
波入射角对越浪量的影响如图8 所示。

图8 波浪入射角对越浪量的影响Fig.8 Effects of the incident wave angle on overtopping
由图8 可以看出,波向往S 向偏转11.25°后,波向角减小11.25°。K2~K3堤段越浪量有所增大,最大增加约15%,但沿线增大幅度不同。东南侧θ <40°,越浪量增加较多;西北侧θ >40°,越浪量增加较少。
2.5 断面试验与局部整体模型试验对比
取K2~K3之间堤段为主要研究对象,波浪正向入射,试验段堤轴线与来波方向垂直。取K2~K3之间断面,断面形式见图1。在100 年一遇潮位及Hs= 3.43 m,T = 10.1 s、墙顶高程7.0 m 和7.5 m下,开展局部整体与断面物理模型试验。两次越浪量对比结果见表4。

表4 越浪量对比成果表Tab.4 Comparison of the overtopping calculated by different formulas
由表4 可以看出,受取土区开挖影响,沿试验堤轴线由东向西,靠近开挖区越近的堤段,由于入射波和开挖区折射波叠加,波高相对较大,越浪量也较大。总体上两类试验越浪量大致相当。因此,波浪局部整体物理模型试验,能较好地反映护岸结构波浪的越浪情况。
2.6 断面越浪量的公式计算与物模试验成果比较
在海堤、护岸等海岸工程的设计中,目前多以允许越浪量为控制条件确定堤顶高程。针对海岸工程的越浪量问题,国、内外学者根据大量的物理模型试验研究成果,提出过多种关于海岸工程越浪量的经验公式。文中分别用具有代表性的《海港水文规范》[3]、陈国平[4-5]和Van der Meer[17]公式计算断面在极端高潮位4.63 m,100 年一遇波高Hs=4.07 m,T = 10.1 s;极端高潮位4.63 m,Hs=3.26 m,T = 9.46 s;潮位4.51 m 和Hs= 3.26 m,T =9.46 s 作用下的越浪量,断面形式见图1。并与断面物模试验结果对比,具体结果见表5。

表5 斜坡堤越浪量的公式计算与物模试验结果对比Tab.5 Compartson of the overtopping calculated by formulas and physical experiments on oblique
由表5 可以看出,《海港水文规范》与Van der Meer 计算偏差较大;Van der Meer 采用无防浪墙最大越浪量公式控制,计算结果与无防浪墙高度时相同,与本文试验值相比,计算值偏大5 倍左右。《海港水文规范》未考虑复坡式平台宽度及平台上水深的影响,其计算结果与斜坡式相同,与文中试验值相比,计算值偏大3 倍左右。陈国平公式以波浪爬高和墙顶超高为主要因子,其计算结果与试验值相比偏小,最大偏差在3 倍以内。
3 结 语
1)针对文中研究案例中,在100 年一遇潮位及相应SSE 向波浪作用下,当Hc/Hs<1.0,40°≥θ >20° 时,随着波向角的增大,越浪量明显减小;当Hc/Hs<1.0,θ >40° 时,随着波向角的增大,越浪量先增大后明显减小。当波向角增大11.25°,最大越浪量增加15% 左右。
2)在100 年一遇潮位下,对比波浪正向与斜向入射时的越浪量。波浪斜向入射时,入射波浪在平台上传播距离加长,波浪在平台上破碎,消耗大量的能量。因此与波浪正向入射试验结果相比,显示波浪斜向入射下平均越浪量比正向入射明显减小。文中计算结果表明波浪斜向入射下的越浪量比正向入射时小约一个数量级,有的甚至小二个数量级。
3)通过试验结果与典型的经验公式计算结果比较得出,本工程条件下,陈国平公式计算结果与物理模型试验值相比偏小,《海港水文规范》与Van der Meer 公式计算结果与物理模型试验值相比偏大。
[1]合田良实.港工建筑物的防浪设计[M].刘大中,孙巨才,译.北京:海洋出版社,1983:16-21.
[2]Van der Meer J W.Wave run-up and wave overtopping at dikes[R].Delft Netherlands:J W Van der Meer,2002.
[3]中交第一航务工程勘察设计院有限公司.JTS 145-2-2013 海港水文规范[S].北京:人民交通出版社,2013:67-70.
[4]陈国平,王铮,袁文喜,等.不规则波作用下波浪爬高计算方法[J].水运工程,2010(S1):23-30.
CHEN Guoping,WANG Zheng,YUAN Wenxi,et al. Calculation of wave run-up under the irregular wave action[J]. Port and Waterway Engineering,2010(S1):23-30.(in Chinese)
[5]陈国平,周益人,严士常.不规则波作用下海堤越浪量试验研究[J].水运工程,2010(3):1-6.
CHEN Guoping,ZHOU Yiren,YAN Shichang.Test study on wave overtopping under irregular wave action[J].Port and Waterway Engineering,2010(3):1-6.(in Chinese)
[6]Bruce T,Van der Meer J W,Franco L,et al. Overtopping performance of different armour units for rubble mound break waters[J].Coastal Engineering,2009,56(2):166-179.
[7]Hedges T S.Interpolating H&R wave overtopping coefficients[J].Environmental Studies,2000(5):13-22.
[8]Zanuttigh B,Martinelli L,Lamberti A. Wave overtopping and piling-up at permeable low crested structures[J]. Coastal Engineering,2008,55(6):484-498.
[9]Hawkes P J.Mean overtopping rate in swell and biomodal seas[J].Proceedings of the ICE-Water Maritime and Energy,1999,136(4):235-238.
[10]Geeraerts J,Kortenhaus A,González-Escrivá J A,et al. Effects of new variables on the overtopping discharge at steep rubble mound breakwaters:the zeebrugge case[J].Coastal Engineering,2009,56(2):141-153.
[11]Van Gent M R A,Van den Boogaard H F P,Pozueta B,et al.Neural network modelling of wave overtopping at coastal structures[J].Coastal Engineering,2007,54(8):586-593.
[12]Verhaeghe H,Van der Meer J W,Steendam G J,et al. Wave overtopping database as the starting point for a neural network prediction method[C]//ASCE,Proc Coastal Structures.Portland:America Society of Civil Engineer,2003:418-430.
[13]Owen M W,Steele A A J.Effectiveness of recurved wave return wall[R].Wallingford:Hydraulics Research,1991.
[14]Owen M W.Design of seawalls allowing for overtopping[R].Wallingford:Hydraulics Research Station,1980.
[15]Franco L,De Gerloni M,Van der Meer J W.Wave overtopping on vertical and composite breakwaters[C]//Proceedings of 24thICCE.Kobe,Japan:Coastal Engineering,1994,1(24):1030-1045.
[16]Franco C,Franco L.Overtopping formulas for caisson breakwaters with nonbreaking 3D waves[J]. Journal of Waterway,Port,Coastal,and Ocean Engineering,1999,125(2):98-108.
[17]Van der Meer J W.Wave Run-Up and Overtopping[M].Brookfield:Balkema,Rotterdam,1998:22-36.

