基于最小二乘支持向量机摩擦建模的机电伺服系统动态面控制
陈 强, 楼成林
(浙江工业大学 信息工程学院,浙江 杭州310023)
随着电力电子技术、计算机控制技术、信息技术的飞速发展,伺服系统已经以其优异性能得到广泛应用。但是,由于摩擦环节的存在,伺服系统的性能仍然受到了较大的限制。为了克服摩擦力带来的影响,有必要对摩擦的补偿问题进行研究。
在实际工程中,为了克服摩擦力带来的影响,许多摩擦补偿的方法被提出。向红标等[1]提出了基于LuGre 模型的自适应摩擦补偿。LuGre 模型能够较为准确地反映机械中的摩擦现象,这使得它得到了广泛的应用。然而,由于LuGre 模型需要复杂的参数辨识过程,这使得其在实际的补偿中有很多困难。徐小平等[2]提出了基于神经网络的摩擦力混合模型。该方法引入柔性Sigmoid 函数与RBF 神经网络串联,构造出神经网络混合模型用于实现非线性摩擦特性的智能建模。WANG G L 等[3]提出了具有自适应能力的支持向量网络,并且在线实现了摩擦残余不确定性的补偿,得到了较为理想的仿真效果。林旭梅[4]进一步提出了最小二乘支持向量机的方法,利用最小二乘支持向量机的逼近功能建立摩擦力的模型。
在摩擦补偿的基础上,许多控制方法被提出来。如PID 控制,滑模控制,反步控制等。罗进生等[5]利用支持向量机对PID 的参数进行自整定,实现了对非线性系统的有效控制;刘强等[6]设计了自适应滑模控制器能适应参数的大范围变化,抑制非线性干扰;周金柱等[7]结合支持向量机摩擦建模,使用反步控制法,针对不确定非线性系统,通过逐步修正算法设计控制器,实现系统的全局跟踪;HUANG Sunan 等[8]利用动态面的控制方法,用一个一阶滤波器解决了反步控制法中求导困难的问题。
文中提出一种基于最小二乘支持向量机摩擦建模的机电伺服系统动态面控制方法。该方法通过利用最小二乘支持向量机的逼近功能,对摩擦力进行建模,进而根据建立的模型结合动态面的控制方法设计了控制器,提高了摩擦补偿的效果,仿真研究结果表明了该方法的有效性。
1 系统模型
机电伺服系统通常是电机通过传动比为i 的减速器驱动负载转动,系统的方程为
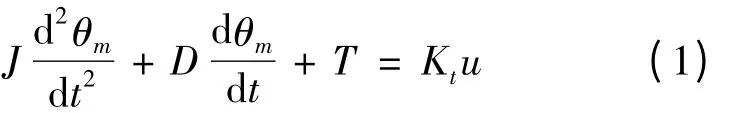
其中,θm,ωm分别为电机输出轴位置和转速;J 和D为折算到电机轴上的等效转动惯量和等效阻尼系数;Kt为电机扭矩常数;u 为控制量;T 为负载摩擦扭矩。摩擦力矩T 可以表示为

其中,Td= β| ωl| + ζ1为摩擦的动态扰动部分;TN为负载速度ωl的静态摩擦力矩函数,文中通过最小二乘支持向量机建立。因此,摩擦模型最终为

其中,ΔT 为摩擦力矩的不确定性,它主要由动态摩擦的扰动误差ζ1和静态摩擦的建模误差组成。整理式(1)和式(3),得到系统的状态空间模型为

2 最小二乘支持向量机摩擦建模
根据伺服系统的实际工作条件,可以确定电机正转和反转的转动速度范围是[0,ωmax]和[ωmin,0];在标称条件下,可以在该速度范围内确定每个速度样本及其对应的摩擦力矩样本数据为
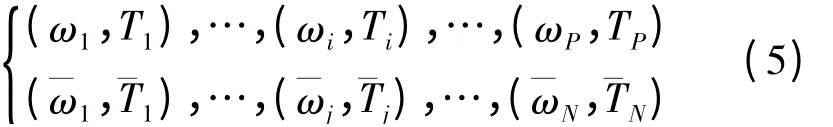
利用标称条件下的样本数据集和最小二乘支持向量机建立以下模型
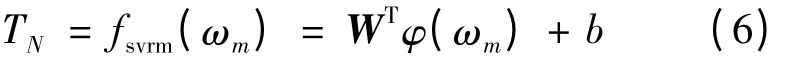
其中,W 为权重矩阵;φ(ωm)为转动速度ωm的核函数。根据式(6),设计拉格朗日函数为
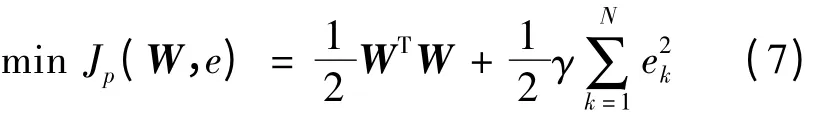
对应每一个转动速度ω 都有

利用最小二乘法可以构造如下等式
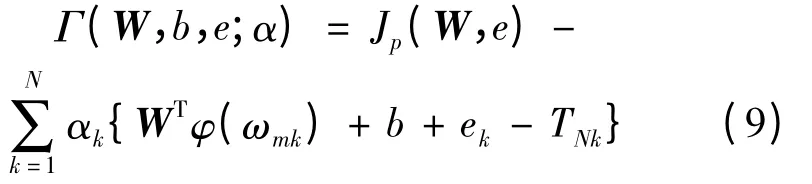
对式(9)各变量求偏导可得
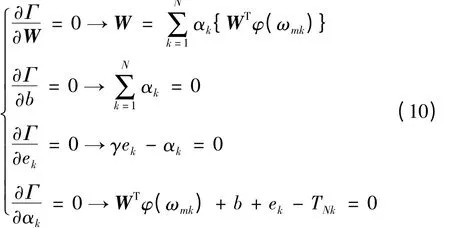
整理式(10)后可得

求解式(11)可得

其中 A = Ω + I/γ。
3 动态面控制器设计
将式(1)改写为

式中:x1= θm为电机输出轴位置;x2= ωm为电机输出轴转速。
定义跟踪误差为

其中,x1d为跟踪参考信号。对式(14)求导,可得
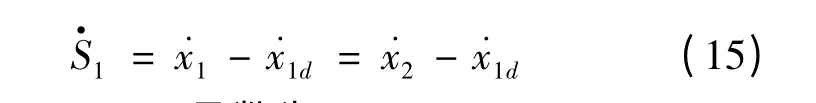
设计Lyapunov 函数为

对式(16)求导得
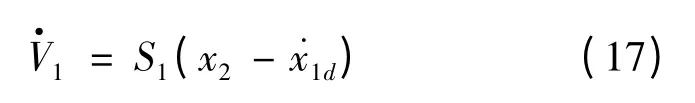

其中,k1>0。
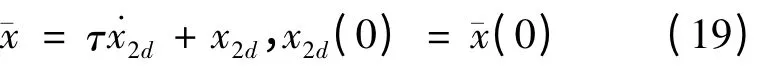
其中,τ >0 为时间常数。定义

设计Lyapunov 函数为

对式(21)求导,并将式(13)、式(19)代入其中得

定义

对式(23)求导得

式(24)可改写为

其中,| f(¨x1d,k1S1)|≤M,M >0 是一个常数。
设计Lyapunov 函数为

对式(26)求导,并将式(22)、式(24)代入计算得


设计控制器u 为

式中:k2>0 为正常数;参数TN可以根据最小二乘支持向量机建模得到TN= fsvrm(ωm);β 和ΔT 为已知参数。
定理1 给定伺服系统式(3)和跟踪误差式(14),选择控制器式(28),则系统跟踪误差一致最终有界。
证 针对系统式(3)设计Lyapunov 函数为

对式(29)求导,并将控制器代入其中可得
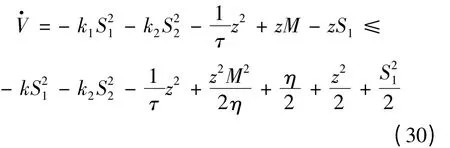
式中,η >0 为常数。
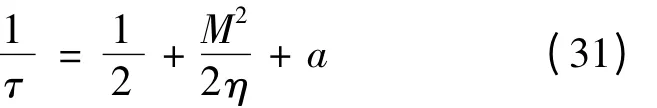
其中,a >0 为一个常数。
将式(31)代入式(30)可以得到

4 仿真结果及分析
为验证所提方法的优越性,文中分别对摩擦力补偿前和补偿后的控制效果进行仿真比较。在仿真中初始条件和部分参数设置保持一致。
仿真中,模型(1)的参数为J = 0.5 kg·m2,D =0.3 N·m·(rad/s),Kt= 1,i = 10;控制器参数选择k1= 5,k2= 5。使用LuGre 摩擦模型仿真获得数据样本,仿真参数为FC= 26 N·m,FS= 36 N·m,ωs=0.517 rad/s,σ0=105N·m,σ =0.5 N·m,σ2= 2 N·m。原数据经过处理得到数据样本集合G。根据样本合集G,使用最小二乘支持向量机建模。
在输入信号为y = sin(t)的作用下,补偿前后的控制效果对比如图1 ~图3 所示。其中:θref为期望信号;θ1和θ2分别为补偿前和补偿后的跟踪信号;e1和e2分别为补偿前和补偿后的跟踪误差。图1给出了系统跟踪效果对比曲线。图2 给出了系统跟踪误差曲线,图3 给出了最小二乘支持向量机摩擦建模曲线。

图1 跟踪效果对比Fig.1 Comparison of the tracking effect
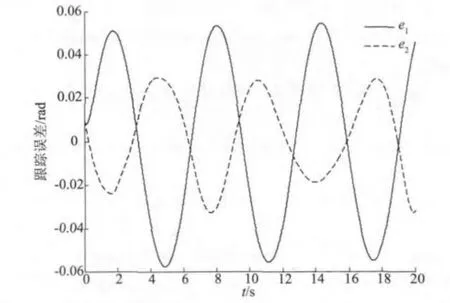
图2 跟踪误差对比Fig.2 Comparison of the tracking errors
由图1 和图2 可以看出,补偿后的位置状态对期望信号的跟踪效果更好,其跟踪误差在± 0.03 rad 范围内变化,小于补偿前的。

图3 最小二乘支持向量机摩擦建模Fig.3 Least squares support vector machine friction modeling
由图3 可以看出,最小二乘支持向量机能比较准确地逼近摩擦力F,其估计误差小于0.04 N。
为更好的体现摩擦力补偿之后的效果,在控制器参数都不变的情况下,改变输入信号,比较两种情况下的跟踪效果。图4 ~图6 分别给出了期望信号为y = sin(t)+ cos(t)的系统跟踪效果对比曲线、系统跟踪误差曲线、最小二乘支持向量机摩擦建模曲线。

图4 跟踪效果对比Fig.4 Comparision of the tracking effect

图5 跟踪误差对比Fig.5 Comparison of the tracking errors
由图4 和图5 可以明显看出,在参数不变,期望信号改变的情况下,补偿前的跟踪误差在± 0.25 rad 范围内变化,而在补偿后,误差在6 s 后稳定在±0.1 rad 范围内。因此,补偿后的跟踪效果更好,跟踪误差更小。

图6 最小二乘支持向量机摩擦建模Fig.6 Least squares support vector machine friction modeling
由图6 可以看出,最小二乘支持向量机能比较准确地逼近摩擦力F,其估计误差小于0.04 N。
5 结 语
文中提出了一种基于最小二乘支持向量机摩擦建模补偿的动态面控制方法,用于解决机电伺服系统摩擦不确定的控制问题,避免了传统方法中的参数辨识,故能使用较少的数据建立模型。根据最小二乘支持向量机设计的动态面控制器可有效地减弱摩擦对与控制性能的影响,提高系统的跟踪精度。
[1]向红标,谭文斌,李醒飞,等.基于LuGre 模型的自适应摩擦补偿[J].机械工程学报,2012,48(17):70-74.
XIANG Hongbiao,TAN Wenbin,LI Xingfei,et al.Adaptive friction compensation based on LuGre model[J].Chinese Journal of Mechanical Engineering,2012,48(17):70-74.(in Chinese)
[2]徐小平,党选举.基于神经网络的电机摩擦力混合模型研究[J].计算机仿真,2012,29(5):178-182.
XU Xiaoping,DANG Xuanju.Study on hybrid friction model for motors based on neural network[J].Computer Simulation,2012,29(5):178-182.(in Chinese)
[3]WANG G L,LI Y F,BI D X. Support vector networks in adaptive friction compensation[J]. IEEE Transactions on Neural Networks,2007,18 (4):1209-1219.
[4]林旭梅.交流伺服系统摩擦力补偿和优化滑模仿真[J].计算机仿真,2014,31 (8):397-401.
LIN Xumei.Simulation on friction compensation and optimal sliding mode control for servo system at low speed[J]. Computer Simulation,2014,31 (8):397-401.(in Chinese)
[5]罗进生,袁喜林,赵凯,等.模糊PID 控制在伺服系统中的应用[J].机械设计与制造,2013(5):229-234.
LUO Jinsheng,YUAN Xilin,ZHAO Kai,et al. Application of fuzzy-PID control in the servo system of CNC machine[J].Machinery Design and Manufacture,2013(5):229-234.(in Chinese)
[6]刘强,冯姝婷,尔联洁. 高精度机械伺服系统的一种新型自适应滑模控制方法[J]. 控制理论与应用,2004,21(2):239-241.
LIU Qiang,FENG Shuting,ER Lianjie. Novel adaptive sliding mode control scheme of high precision mechanical servo system[J].Control Theory and Applications,2004,21(2):239-241.(in Chinese)
[7]周金柱,段宝岩,黄进,等. 伺服系统摩擦的支持向量回归建模与反步控制[J]. 控制理论与应用,2009,26(12):1045-1049.
ZHOU Jinzhu,DUAN Baoyan,HUANG Jin,et al.Support vector regression modeling and backstepping control of friction in servo system[J].Control Theory and Applications,2009,26(12):1045-1049.(in Chinese)
[8]HUANG Sunan,TAN Kok Kiong.Intelligent friction modeling and compensation using neural network approximations[J].IEEE Transactions on Industrial Electronics,2012,59(8):3342-3369.

