三相电压型PWM整流器解耦控制研究

于佳丽，梁 燕，万健如

（1.天津大学电气与自动化工程学院，天津300072；2.重庆能源职业学院，重庆402260）

引言

三相电压型 PWM整流器是并网技术的核心，具有网侧电流正弦化、功率因数单位化以及能量可双向流动等优势，广泛应用在国防科技、工业生产、农业以及日常生活中［1］。

三相电压型PWM整流器采用直接功率控制DPC（direct power control），具有高功率因数、动态响应快、算法和结构简单等优点。但传统滞环DPC方法中，开关表只由6个基本电压矢量组成，使得有功和无功功率的调节效果不理想。针对这个问题文献［2］提出优化开关表法，仍存在开关频率不固定的问题；为了实现定频的目的，文献［3］提出将SVPWM与DPC相结合，但网侧瞬时功率之间存在交叉耦合的问题，并且系统稳定性受PI参数影响大，抗扰动能力不理想；为了改善DPC的性能，文献［4-7］分别提出功率前馈解耦控制、无源控制、预测控制、模糊滑模控制，上述算法的共同特点是基于d-q坐标系，需要采用锁相环对电网电压进行准确定向，增加了系统控制的复杂程度；文献［8］提出两相静止坐标下的直接功率控制，省去了锁相环，因为系统相关变量稳态时为正弦量，PI调节器无法实现无静差控制，文中提出采用比例谐振控制，但是参数整定比较复杂，而且实际系统中电网频率会有0.5%的偏差，理想的比例谐振控制器不易实现；针对电网不平衡情况，文献［9-10］分别提出静止坐标下的预测功率控制和谐振滑模控制，取得较好控制效果，但实际系统中电感中的漏感以及测量装置精度问题会导致测量电感与实际电感之间存在偏差，会影响系统的控制性能。

为了对整流器进行更好的控制，针对两相静止坐标下系统强耦合和非线性问题，本文首先设计了反馈线性化DPC，该算法可以较好地实现瞬时功率解耦，但是电感参数出现偏差时对解耦控制效果产生一定影响。针对这一问题，本文提出一种自抗扰DPC的改进措施，能够提高系统鲁棒性。通过仿真对比分析了两种控制方法的优缺点。

1 三相电压型PWM整流器数学模型

图1为三相电压型PWM整流器的主电路，其在两相静止坐标系下的数学模型为

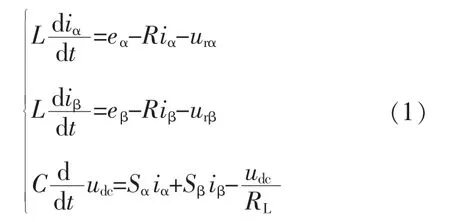
式中：eαβ、iαβ为电网电压和电流的 αβ 分量；Sαβ为整流器在 αβ 坐标系下的开关函数；urα、urβ分别为整流器交流输入电压 αβ 分量，urα=Sαudc，urβ=Sβudc；udc为整流器直流母线电压；L为网侧电感；R为网侧电阻；RL为负载电阻。

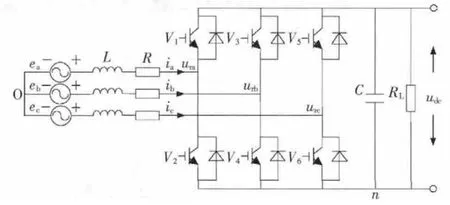
图1 三相电压型PWM整流器主电路Fig1.Main circuit of three phases voltage source PWM rectifier

为了实现PWM整流器无网侧电压传感器运行，在此引入虚拟磁链的概念。虚拟磁链是由虚拟电机所引出的，将网侧电源看成是一个虚拟交流“电机”，其中R、L看成是虚拟电机的定子电阻和电感，认为线电压 urα、urb、urc由虚拟磁链产生的。 忽略交流侧电阻压降，虚拟磁链可表示为

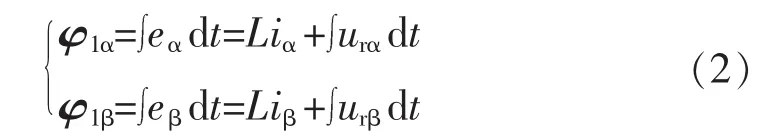
式中，φ1α、φ1β分别为整流器网侧虚拟磁链矢量 φ1的α轴分量和β轴分量。

虚拟磁链算法中积分器具有滤除高次谐波的作用，但是在实际中纯积分环节会引起直流偏移问题。本文采用一阶惯性环节代替纯积分，同时进行适当补偿［1］，虚拟磁链观测器如图2所示。其中，ωc为截止频率，ω为电网频率。

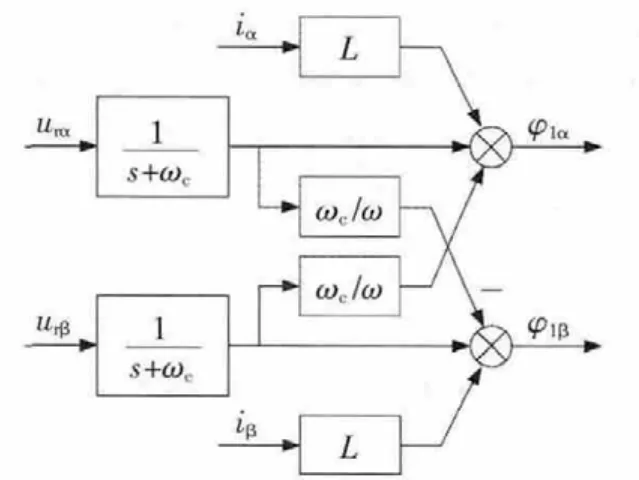
图2 虚拟磁链观测器Fig.2 Observer of virtual flux

假设三相电网电压对称，幅值和角频率不变，则静止坐标下电网电压与虚拟磁链的关系为

利用改进虚拟磁链观测器和式（3）就可以估计电网电压。根据瞬时功率理论，将PWM整流器网侧瞬时功率表示为

假设电压型PWM整流器为理想模型，忽略它的损耗，根据功率不变原则有

于是得到PWM整流器的数学模型为

2 功率内环控制

2.1 反馈线性化设计

PWM整流器的控制目标之一是实现网侧电流正弦化，单位功率因数运行。对于传统旋转坐标系下的直接功率控制系统，由于扰动和控制量都为直流量，采用PI控制就可以获得很好的效果；缺点是需要锁相环，当电网电压出现扰动时，会影响相位检测和系统的控制性能。本文讨论的静止坐标系下直接功率控制系统，省去了锁相环，同时采用虚拟磁链技术省掉了网侧的电网电压传感器，但该系统存在强耦合和非线性，系统的相关变量在稳态下是正弦量，而非直流量，PI调节器无法做到无差调节。而反馈线性化是仿射非线性系统线性化和解耦控制的有力手段，下面首先应用反馈线性化理论进行功率内环设计，为此需建立系统有功和无功功率的仿射非线性模型， 取状态变量，x=［x1x2］T=［p q］T控制变量 u=［u1u2］T=［urαurβ］T，输出变量 y=［y1y2］T=［pq］T。 根据式（6），则输入输出仿射非线性模型为

对输出变量求导得

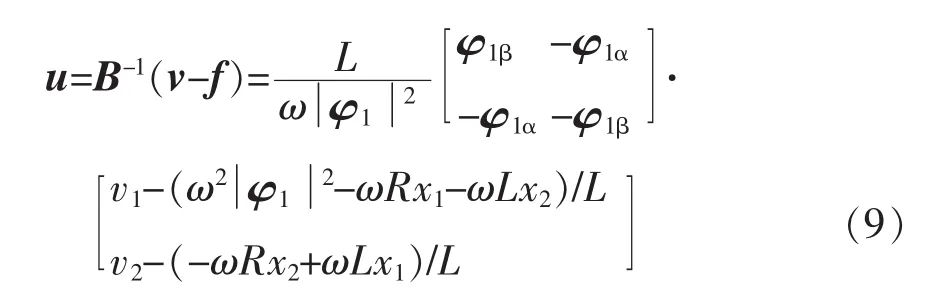
式中，v=［v1v2］T为新的控制变量。则得到反馈线性化后系统为一阶积分器，即

为了跟踪期望输出，选取新的输入v使其满足

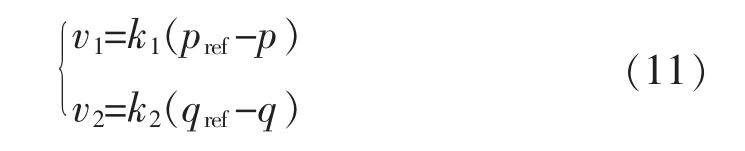
式中：pref为有功功率给定值，为电压外环输出，为了控制网侧单位功率因数运行；qref为无功功率给定值，qref=0；k1、k2为正的可调参数，为了使系统响应足够快，稳态误差足够小，一般取值较大。

反馈线性化控制框图如图3所示。首先，根据直流母线电压及上一时刻的开关信号计算得到变量urα和urβ，利用霍尔传感器测得网侧两相电流，根据虚拟磁链观测器估计出电网电压，利用式（4）计算出瞬时功率的实际值，结合式（9）得到控制量urα和urβ，送入SVPWM模块产生开关信号，实现对整流器的定频控制。

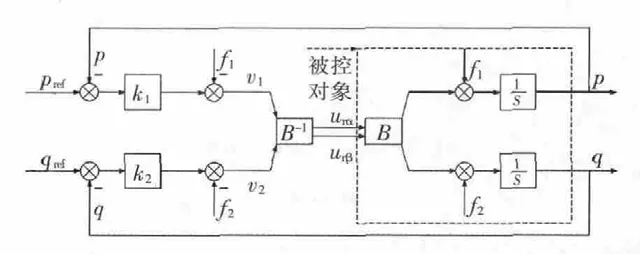
图3 反馈线性化控制框图Fig.3 Block diagram of feedback linearization controller

2.2 自抗扰设计

根据第2.1节的分析，基于反馈线性化理论可以精确计算出扰动量，进而实现解耦控制，但是该算法对系统参数具有较强的依赖性，实际电感中含有漏感，不能准确知道电感参数时，计算的扰动会出现偏差，不能精确补偿实际扰动，这势必会影响整流器的控制性能。自抗扰控制器［11］能够估计系统中的扰动并做出补偿，对控制对象的参数变化和不确定扰动具有很强的适应性和鲁棒性。所以本文提出自抗扰改进直接功率控制。设计中省略TD环节，自抗扰控制器由1个二阶非线性扩张状态观测器ESO和1个一阶线性状态误差反馈控制器组成。为了便于控制器设计，引入虚拟控制量h=［h1h2］T，根据式（7），则系统方程转化为

式中：ΔL为电感参数测量误差；g为系统总扰动，

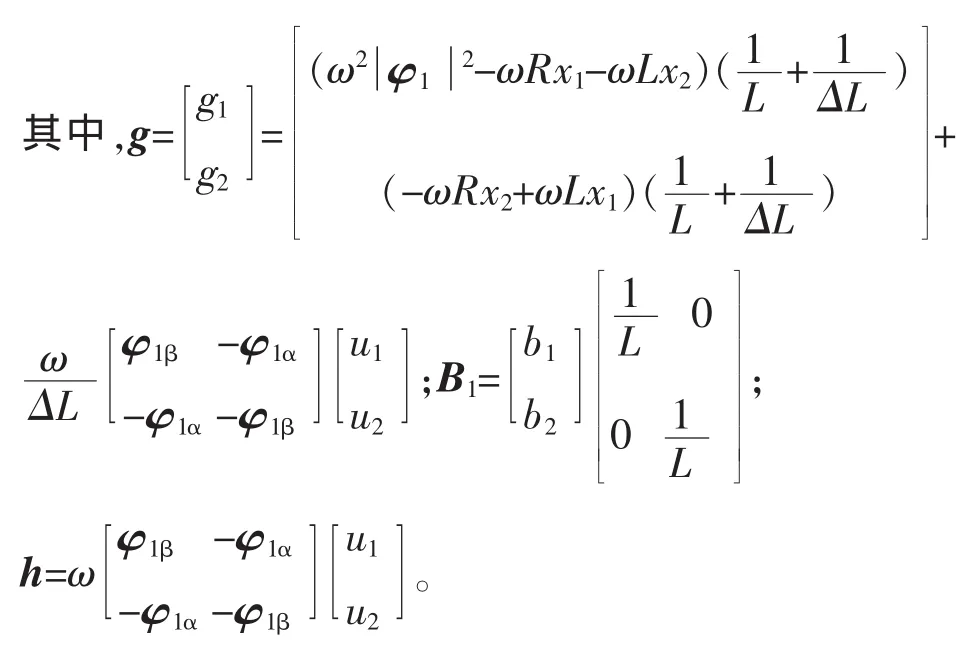
瞬时有功和无功功率的二阶非线性ESO分别为

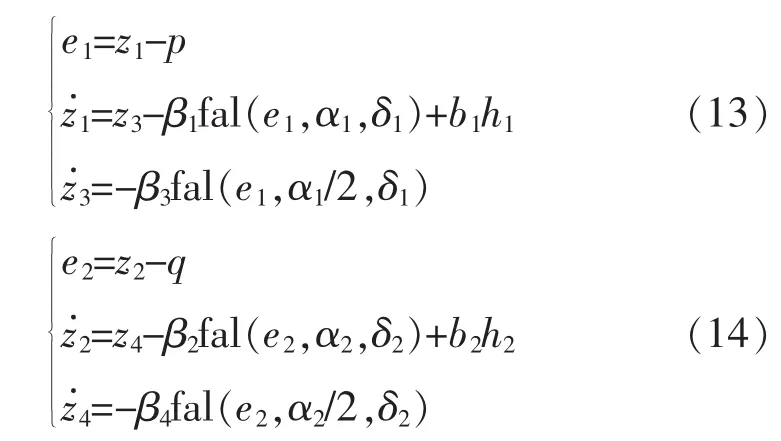
式中：z1、z2为输出的观测值；z3、z4为扰动 g1、g2的观测 值 ；e1、e2为观测误差；β1、β2、β3、β4分别为二阶ESO的参数；fal（）为非线性函数，其表达式为

式中，sgn（·）为符号函数；fal（）函数根据误差大小来调整控制增益，当α＜1时，具有误差小时增益大而误差大时增益小的特点， 本文取 α1=α2=0.5；δ为滤波因子，本文取 δ1=δ2=，其中fs为开关频率。

首先根据线性状态观测器设计参数的初值，则系统瞬时有功和无功功率的二阶线性ESO分别为

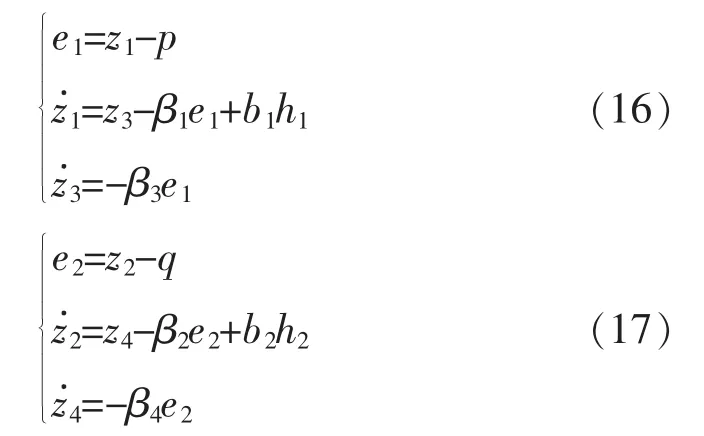
瞬时有功功率的二阶线性ESO的状态方程为

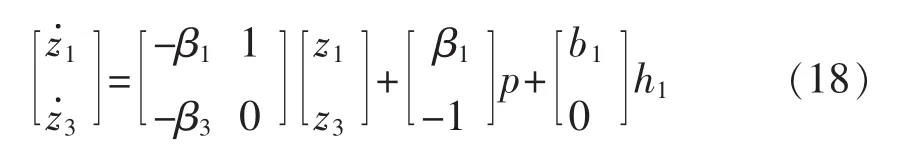
同理，有

式中，ω1、ω2为观测器带宽。在实际中根据观测效果适当的调整参数的取值。

通过对二阶非线性ESO的设计，使得观测器能够很好地估计状态和扰动， 即 z1→p，z3→g1；z2→q，z4→g2。 设定新的输入 w2、w3，使得

对于式（19）的线性系统，只需设计一个比例控制即可，得到的虚拟控制量为

式中，k3、k4为可调参数，为了保证系统稳定必须均为正数。则最终的控制器为

自抗扰控制框图如图4所示。与反馈线性化类似，有功功率给定值pref为电压外环输出，无功功率给定值qref为0。利用式（4）计算出瞬时功率的实际值。实际瞬时功率与上一时刻的虚拟控制量作为非线性ESO的输入，通过非线性ESO估计出功率和扰动量，根据式（23）得到控制量 urα和 urβ，通入SVPWM模块产生开关信号，实现整流器的定频控制。

3 电压外环设计

直流侧电压方程如式（5），为了便于控制器设计，变形为

因为有功功率与直流母线电压有关，设计的电压外环控制器以u2dcref、u2dc为输入，有功功率给定值pref为输出，即

式中：kp、ki为可调参数，取为正数；u2dcref为直流母线电压参考值的平方。

4 仿真分析

在Matlab/Simulink环境下对2种解耦控制方法分别进行了仿真，并对仿真结果进行对比分析。电网电压是峰值85 V、频率50 Hz的理想三相正弦波。功率开关频率fs=5 kHz，网侧滤波电感L=4 mH，直流母线电容 C=2 200 μF，负载电阻 RL=100 Ω，直流电压指令值300 V。仿真步骤如下：

步骤1 验证2种方法对网侧瞬时功率的解耦性。有功功率给定值在900 W到1 600 W之间切换，无功功率给定值在t=0.3 s由-100 var阶跃到100 var，不加电压外环，其他参数不变。2种算法的网侧瞬时功率跟踪效果如图5所示。从图5中可以看出，两种算法有功和无功功率能够快速准确地跟踪给定参考信号，稳态下的波动都能满足要求，在t=0.2 s有功功率跳变时对无功功率没有产生影响，实现有功和无功功率的解耦控制。与反馈线性化DPC相比，自抗扰DPC方法中功率波动更小，调节过程中动态响应更快，使得PWM整流器的性能更优越。

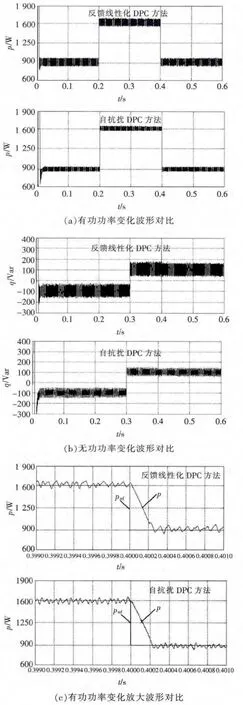
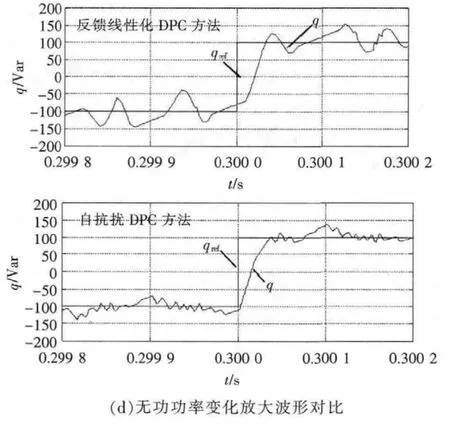
图5 2种算法网侧瞬时功率跟踪效果对比Fig.5 Comparison of tracking effects of instantaneous power in the network side using two different algorithms

步骤2 验证两种方法对负载变化的鲁棒性。在 t=0.3 s时， 负载由原来的 100 ω加载 50 Ω，负载变化时2种算法控制效果对比如图6所示。由图6（a）可以看出，负载变化时2种算法的直流母线电压均发生跌落，大小为2 V，但很快就恢复到稳态值 300 V；由图6（b）、（c）可以看出，自抗扰 DPC 方法中有功和无功功率稳态误差小，负载变化时有功功率超调小，动态响应快。仿真结果表明，自抗扰DPC方法比反馈线性化DPC方法具有更好的抗负载扰动能力。

步骤3 验证2种方法对系统参数变化的鲁棒性。在t=0.3 s时，电感参数由原来的4 mH变为2 mH，其他参数不变，电感参数变化时2种算法控制效果对比如图7所示。由于虚拟磁链观测器依赖于电感参数，当电感参数发生变化时相当于额外增加了电网电压扰动，从图7（a）可以看出，电感参数变化时两种中直流母线算法中直流母线电压几乎没有受到影响；由图7（b）、（c）可以看出，反馈线性化DPC方法中放大器的放大倍数为100 000，自抗扰DPC方法中放大倍数明显减弱，只需要5 000就可以，并且有功和无功功率稳态误差更小，对参数变化敏感性降低；由图7（d）可以看出，A相的电压电流始终同相位，满足网侧单位功率因数运行，通过对网侧电流畸变率THD进行FFT分析可以得到，采用反馈线性化DPC时，参数变化导致网侧电流THD由3.88%增加到5.73%，超出了绿色整流器THD＜5%的限制，而采用自抗扰DPC后，电感参数变化使得网侧电流THD由2.43%增加到2.37%，仍满足绿色整流器的要求。从图7（e）可以看出，在参数变化后，两种算法中虚拟磁链都能很快恢复稳定。综合来看，自抗扰DPC的方法比反馈线性化DPC具有更强的抗系统参数变化的能力。

图6 负载变化时2种算法控制效果对比Fig.6 Comparison of controlling effects with varying loads using two different algorithms

图7 电感参数变化时2种算法控制效果对比Fig.7 Comparison of controlling effects with varying inductances using two different algorithms

5 结语

本文在PWM整流器两相静止坐标数学模型基础上，设计的反馈线性化DPC方法和自抗扰DPC方法都能够对网侧瞬时有功和无功功率进行解耦。当负载突变时，2种算法都具有一定的抗负载扰动能力。但当整流器电感参数发生变化时，由于反馈线性化DPC方法自身的局限性，会影响系统的控制性能，针对这一问题设计的自抗扰改进DPC能够实时估计并且补偿系统中的扰动，使得系统动态响应更快速，网侧电流谐波畸变率更低，更好地改善了系统性能。

［1］李昆鹏.双PWM变换器协调控制策略及工作性能研究［D］.天津：天津大学，2014.Li Kunpeng.Research on Coordinated Control Strategy and Performance of Dual PWM Converter［D］.Tianjin：Tianjin University,2014（in Chinese）.

［2］万健如，宫成，李昆鹏，等.电压型PWM整流器预测直接电容功率控制研究［J］.电力系统保护与控制，2013（3）：96-101.Wan Jianru,Gong Cheng,Li Kunpeng,et al.Research on predict direct capacitor power control of voltage source PWM rectifier［J］.Power System Protection and Control，2013（3）：96-101（in Chinese）.

［3］杨达亮，卢子广，杭乃善,等.三相电压型PWM整流器准定频直接功率控制［J］.中国电机工程学报，2011，31（27）：66-73.Yang Da Liang,Lu Zi Guang,Hang Nai shan,et al.Novel quasi direct power control for three-phase voltage-source PWM rectifiers with a fixed switching frequency［J］.Proceedings of the CSEE，2011，31（27）：66-73（in Chinese）.

［4］Li Mingshui,Wan Jianru,Li Guangye.Research on power feed forward control strategy of PWM rectifier［C］.2011 4th International Conference on Power Electronics Systems and Applications.Hongkong，China，2011.

［5］徐升升，王久和，慕小斌,等.基于EL模型的三电平电压型PWM整流器的无源与PI相结合控制方法研究［J］.电源学报，2011，9（6）：45-48.Xu shengsheng,Wang jiuhe,Mu xiaobin,et al.Research on the method of passivity combined with PI control of three level voltage source PWM rectifier based on EL model［J］.Journal of Power Supply，2011，9（6）：45-48（in Chinese）.

［6］张永昌，谢伟，李正熙，等.PWM整流器功率脉动最小化方法的研究［J］.中国电机工程学报，2013，33（18）：57-64.Zhang Yongchang,Xie Wei,Li Zhengxi,et al.Studies on power ripple minimization of PWM rectifiers［J］.Proceedings of the CSEE，2013，33（18）：57-64（in Chinese）.

［7］Huang Jingjing,Zhang Aimin,Zhang Hang,et al.Improved direct power control for rectifier based on fuzzy sliding mode［J］.IEEE Transactions on Control Systems Technology,2014,22（3）：1174-1180.

［8］李子欣，李耀华，王平，等.PWM整流器在静止坐标系下的准直接功率控制［J］.中国电机工程学报,2010,30（9）：47-54.Li Zixin,Li Yaohua,Wang Ping,et al.Novel quasi direct power control method for PWM rectifier in stationary frame［J］.Proceedings of the CSEE，2010,30（9）：47-54（in Chinese）.

［9］全宇，年珩.不平衡及谐波电网下并网逆变器的谐振滑模控制技术［J］.中国电机工程学报，2014,34（9）：1345-1352.Quan Yu,Nian Heng.Resonance-based sliding mode control of grid connected inverters under unbalanced and harmonic grid voltages［J］.Proceedings of the CSEE，2014,34（9）：1345-1352 （in Chinese）.

［10］Zhang Yongchang,Qu Chongqi.Direct power control of a pulse width modulation rectifier using space vector modulation under unbalanced grid voltage［J］.IEEE Tramsaction on Power Electrónics,2015,30（10）：5892-5901.

［11］Han Jingqing.From PID to active disturbance rejection control［J］.IEEE Transactions on Industrial Electronics,2009,56（3）：900-906.