论小学数学思维训练

陈翔

数学思维是数学的灵魂，没有思维的数学课堂就像没有绿色的森林，没有思维的参与和训练就不能说学习了数学。作为小学数学教师不单要教会学生数学基本知识，更重要的是培养学生的数学思维。要让学生在数学问题中不断思考、前进，再思考、再前进，在数学特有的曲折中体会数学的变化美。

一、设置不同情境，让学生在情境的变化中锻炼思维

针对相同的教学内容，教师利用不同的视角设置不同的情境模式，让学生在具体的情境中，利用自己的数学知识解决数学问题，从而锻炼学生的思维。

例如，在讲解“多边形的面积计算”（苏教版五年级）设计这样一个情境：教师拿出一幅多边形的图：“同学们，老师家需要进行装修，这是老师家客厅的平面图（如图1所示），我需要按照多大面积准备瓷砖呢？哪位同学可以帮老师想想办法？”这时候，学生会给出各种各样的方法，例如分成一个长为7米、宽为3米的长方形和一个长为4米、宽为3米的长方形，分别计算这两个长方形的面积，再求和。有的学生分成长为6米、宽为4米的长方形和边长为3米的正方形。这些方法仅仅是求多边形面积的方法之一。因此教师继续构建新的情境：“同学真聪明，帮老师解决了大难题。我还有一个问题，希望同学们也能帮我想想办法。这是我儿子班级联欢会的彩旗（如图2所示），每个学生做3面，我需要给他准备多大面积的原材料呢？”

这时候，学生又展开新一轮讨论，有一名学生提出：可以补成一个长20厘米、宽15厘米的大长方形，然后再减去直角三角形的面积。至此，探究多边形面积的计算方法学生就都得出了。

可见教师只有精心设计情境，在不断变化的情境中，让学生去探究体验，才能达到锻炼学生思维的目的。

二、设置层层递进的问题，让学生在破解谜题中锻炼思维

数学课堂就是由一个个问题连接而成的，教师应该巧妙地设计具有一定梯度的问题，让学生在解决一个个问题的过程中体验快乐，同时获得思维训练。

例如在讲解分数、百分数时，为了让学生准确找到数量对应的单位“1”，教师可以设计这样的一系列问题。甲班有40人，乙班有50人。（1）甲班是乙班的几分之几？（2）乙班是甲班的几分之几？（3）甲班比乙班少几分之几？（4）乙班比甲班多几分之几？（5）甲班有40人，比乙班多1 / 5，乙班有多少人？（6）甲班有40人，乙班比甲班多1 / 4，乙班有多少人？这些问题，不断变化数量对应的单位“1”，让学生通过对这些问题的逐一思考解决，巩固判断单位“1”的方法。

三、把主动权还给学生，让学生自我锻炼思维能力

现在的数学教学更注重于开放性和发散性思维的训练，因此教师要给学生设置开放性的试题，把解决问题的主动权还给学生，也只有这样，学生的思维才能得到极大地锻炼。

以“认识比”的复习课为例，教师可以设计这样的开放性试题“学校的桌子每张100元，椅子每把60元，请你说出课桌椅之间的关系。这样的题没有明确的问题，就是让学生去自己体会，学生只有把“比的认识”学扎实和学透彻，才能把二者之间的关系列清楚，不同的学生会有不同的判断，如，桌子和椅子的价格比是5∶3;椅子和桌子的价格比是3∶5;椅子价格是桌子价格的3 / 5，桌子价格是椅子价格的5 / 3，桌子价格占桌椅总价格的5 / 8，椅子占桌椅总价格的3 / 8，桌子比椅子贵2 / 3，椅子比桌子便宜2 / 5，等等。教师在学生总结完二者的关系后，继续提出新的问题“你能利用自己所列的关系，提出问题吗？你能解决自己提出的问题吗？”

开放性问题能把问题的设计和问题的解决都还给学生，使学生在多种问题和多种答案中自由穿行，获得多向思维的训练和综合归纳能力的提高。

四、让学生在总结中发现数学规律，提高数学思维能力

规律往往隐藏在现象中，教师要善于让学生拨开层层迷雾，发现数学知识的本质，从而让学生养成良好的总结反思习惯，促进学生思维能力的发展。

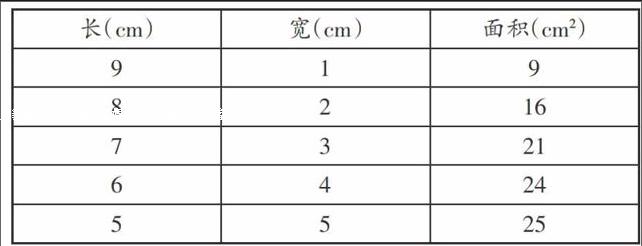
例如教师对于学生不能理解“长方形和正方形周长相同，正方形的面积较大”这个知识点，可以出示这样一道题：用一根长20厘米的铁丝围成不同的长方形，他们的面积是多少？你是怎样围的？学生会给出以下几种情况：

[长（cm）＼&宽（cm）＼&面积（cm2）＼&9＼&1＼&9＼&8＼&2＼&16＼&7＼&3＼&21＼&6＼&4＼&24＼&5＼&5＼&25＼&]

教师引导学生分析表格中的数量，提出：“你发现了这些数字的什么秘密？你能解开这些密码吗？”学生通过讨论发现，所找到的图形面积逐渐增大，同时图形也越来越趋于正方形，从而可以知道，在周长相同的情况下，正方形面积较大。

数学教学中学生思维的训练是一个常说常新的话题，每个数学教师应该将其贯穿于整个数学课堂，让学生在一次次的曲折变化中体会思维改变的美，从而让学生得到数学思维的锻炼。

（责编 金 铃）endprint