钢管混凝土系杆拱桥设计探讨
常 诚
(山西省交通科学研究院,山西 太原 030006)
1 上部结构简介
某钢管混凝土系杆拱桥计算跨径78 m,拱轴线为二次抛物线,矢跨比为1/5,矢高15.6 m,设计时采用刚性系杆刚性拱,柔性吊杆体系。全桥横向左右分幅布置,为横向不对称结构,半幅桥面布置为0.25 m(栏杆)+4.5 m(人行道及非机动车道)+0.25 m(栏杆)+1.2 m(系杆)+0.5 m(防撞护栏)+11.5 m(机动车道)+0.5 m(防撞护栏)+1.2 m(系杆)=19.9 m。全桥上部结构立面、平面如图1、图2所示。

图1 上部结构立面图(比例:1∶250)
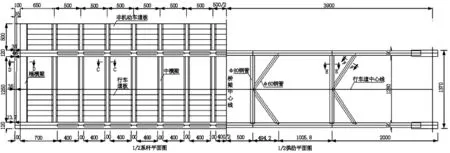
图2 上部结构平面图(比例:1∶250)
全桥拱肋截面由2根钢管(φ900×12 mm)和中间缀板焊接成哑铃型,缀板用两块厚14 mm钢板(外边距450 mm)组焊成,拱肋截面高度为2.2 m,宽度0.9 m,圆钢管和中间缀板内充C40微膨胀混凝土。系杆采用高2.3 m、宽1.2 m、壁厚0.3 m的箱形截面。全桥共17对吊杆,吊杆中心线间距5.0 m,内侧吊杆采用PESFD7-55的镀锌高强钢丝索,外侧吊杆采用PESFD7-73的镀锌高强钢丝索。中横梁高为0.6~1.4 m,宽 0.6 m;端横梁采用箱型断面,高1.0~1.95 m,宽1.9 m;桥面单向2.0%横坡通过横梁高度的变化进行调整;桥面板采用实心板,中板宽0.99 m,厚 0.25 m,边板宽 0.995 m和 1.245 m,厚0.25 m。全桥每幅共设4道K撑,由外径φ800和φ600的钢管焊接而成,壁厚1.2 cm。系杆和横梁均为预应力混凝土构件。外侧系杆内设有20束预应力束,中性轴以下为10φs15.2钢绞线,中性轴以上为9φs15.2钢绞线;内侧系杆内设有16束预应力束,全部为9φs15.2钢绞线;端横梁每根布设6束7φs15.2钢绞线;中横梁每根布设4束7φs15.2钢绞线,所有钢束张拉控制应力为1 339 MPa。
2 静力计算模型
本文采用桥梁有限元计算软件Midas Civil 2006进行全桥静力计算:拱肋为钢管混凝土组合截面,采用主截面(空钢管)和附加截面(上下管核心混凝土和腹腔混凝土)来模拟,来考虑钢管和核心混凝土不同材料、不同施工工序、不同材料龄期对组合截面应力重分布的影响。即考虑空钢管和核心混凝土共用节点,但忽略钢管对核心混凝土的套箍作用。刚刚泵送的混凝土不考虑其对组合截面的刚度贡献,仅考虑其自重,混凝土龄期过后才考虑其参与结构受力。系杆为预应力混凝土构件,吊杆为桁架单元。全桥计算模型如图3所示。全桥共分为358个单元,共304个节点。

图3 桥梁Midas Civil 2006静力计算模型
具体计算时,根据施工过程全桥划分了以下施工阶段形成结构体系:搭支架分3段浇注系杆,浇注全部端横梁、中横梁;张拉端横梁预应力钢束;张拉中横梁第一批预应力钢束;张拉系杆第一批预应力钢束;安装拱肋钢管及风撑钢管;泵送下钢管混凝土;泵送腹腔混凝土;泵送上钢管混凝土;按顺序初次张拉吊杆;张拉第二批系杆预应力钢束;安装行车道板;张拉中横梁第二批钢束;拆除系杆施工支架;张拉第三批系杆预应力钢束;对吊杆按相应顺序进行二次张拉;浇注桥面混凝土、护栏及沥青混凝土铺装;收缩徐变10年。
计算过程中,车道荷载按公路-I级考虑;人群荷载取3.5 kN/m2;风力、温度荷载等根据桥梁实际地理位置按相关规范[2]取值。
按照上面结构模型的单元划分、施工过程和设计荷载,对全桥进行内力分析。
3 静力计算结果
3.1 施工阶段系杆各控制截面应力验算
经计算,系杆在施工阶段上缘出现0.25 MPa拉应力,最大压应力为12.6 MPa,均满足规范设计容许值。
3.2 运营阶段各构件应力验算
3.2.1 拱肋
经计算,拱肋截面均为压应力。内侧拱肋钢管的最大应力为131.0 MPa,核心混凝土的最大压应力为5.4 MPa;外侧拱肋钢管的最大应力为186 MPa,核心混凝土的最大压应力为9.1 MPa,均小于规范要求的容许值。
3.2.2 吊杆
经计算,内侧吊杆最不利状态下的最大拉力为953 kN,出现在第4对吊杆上,其破断索力为3 535 kN,安全系数为 3 535/953=3.7>2.5;外侧吊杆最不利状态下的最大拉力为1 622 kN,出现在第5对吊杆上,其破断索力为4 692 kN,安全系数为4 692/1 622=2.9>2.5,故按照容许应力法来计算,吊杆的强度满足要求。
3.2.3 系杆
3.2.3.1 持久状态正常使用极限状态荷载组合结构验算
a)正截面抗裂验算 经计算,本桥在正常使用极限状态系杆截面均未出现拉应力,满足全预应力混凝土构件要求。
b)斜截面抗裂验算 经计算,正常使用极限状态系杆截面最大主拉应力为0.9 MPa,满足全预应力混凝土构件斜截面抗裂σtp≤0.4ftk=1.06 MPa的要求。
c)挠度验算 经计算,外侧系杆在正常使用短期效应组合下,最大挠度为2.58 cm。考虑荷载长期效应影响后,最 大挠度为 ηθ·f=1.425×2.58=3.68 cm。结构自重产生的长期挠度为2.53 cm,系杆的跨中挠度为3.68-2.53=1.15≤78/600=13 cm,最大挠度满足要求。
内侧系杆在正常使用短期效应组合下,最大挠度为1.50 cm。考虑荷载长期效应影响后,最大挠度为ηθ·f=1.425×1.5=2.14。结构自重产生的长期挠度为1.43 cm,系杆的跨中挠度为2.14-1.43=0.71≤78/600=13 cm,最大挠度满足要求。
3.2.3.2 持久状态构件应力验算
a)正截面混凝土法向压应力验算 经计算,内侧系杆上缘最大压应力为14.5 MPa,下缘最大压应力为10.3MPa,外侧系杆上缘最大压应力为16.0MPa,下缘最大压应力为11.2 MPa,均没有超过规范容许值。
b)斜截面混凝土主压应力验算 弹性阶段,内侧系杆大部分截面混凝土的主压应力在13~14 MPa左右,在1/4跨径附近处达到最大值14.5 MPa;外侧系杆大部分截面混凝土的主压应力在14~15 MPa左右,在1/4跨径附近处达到最大值16.0 MPa;均满足规范要求。
c)受拉区预应力钢筋应力验算 预应力钢束在施工阶段和使用阶段的应力验算结果表明,钢束拉应力均符合规范要求。
3.2.3.3 承载能力极限状态荷载组合下结构强度验算
经计算,构件各个截面的承载能力均匀大于作用效应组合值乘以结构重要性系数,强度满足要求。
3.3 全桥弹性稳定计算
弹性稳定性分析同样采用空间有限元程序Midas Civil 2006。拱肋、风撑、横梁均采用梁单元,吊杆采用桁架单元。桥面板自重采用杠杠原理施加在横梁上。全桥共分为296个节点,410个单元,分析中计入了剪切变形和几何刚度的影响。
使用通用程序计算结构的稳定性,实际是按成桥状态直接计算结构内力进而算出稳定系数的,这相当于满堂支架全部结构一次落架的稳定系数。对于本桥,由于实际施工过程中拱肋的累积恒载内力会大于上述情况,因此计算出的稳定系数也会大于实际值。为了纠正上述偏差,在平面杆系计算中对于实际施工过程中拱肋轴力和一次落架中拱肋轴力分别作了计算和对比,前者约比后者大10%。因此,在空间稳定计算中对拱肋的恒载内力计入提高系数1.1,由此计算的稳定系数将符合实际情况[3]。
全桥在偏载的时候,稳定系数最低,也就是拱肋所受到的轴力最大的时候,结构最不安全。经过试算,取出拱肋所受轴力最大的工况进行结构稳定计算。主要计算结果如表1所示。
从计算结果来看,结构的稳定安全系数均大于4,稳定安全性满足要求。
4 结语
a)稳定性分析是系杆拱桥的控制性设计因素之一,本文进行的弹性稳定计算结果是基于理想状况的理论限值,与实际情况有一定的不同。而基于非线性分析的第二类稳定问题更为准确,但由于其计算复杂在工程上应用较少,可对此做更为深入的研究。
b)本文设计过程中未进行横梁的结构安全验算、吊杆的疲劳分析、拱脚及主梁吊点局部应力分析、全桥的行车动力性能分析和抗震性能分析等,还需做进一步研究。
限于篇幅及作者知识水平有限,文中观点难免有不足之处,写作本文的目的是希望跟同行更好地讨论交流,以利于做出更好的设计。

